架桥机刚度对节段胶拼简支梁桥受力影响分析

赵成龙

(中铁十九局集团第二工程有限公司 辽宁辽阳 111000)

1 引言

简支桥梁节段胶拼施工工艺具有施工速度快、节段梁体制作质量易控制、节段重量轻、施工过程减少噪声和灰尘等优点[1－2]，广泛应用于城市桥梁施工中[3]，对此国内外诸多学者对该种施工技术做了大量可靠性和创新性研究[4－5]。

张雷以节段预制胶拼40＋56＋40 m预应力混凝土连续梁桥为工程背景，提出节段预制拼装连续梁桥结构的构造措施、结构检算技术标准、拼装工艺要求[6]。杨继光对节段预制胶拼主梁构造、强度、刚度等提出了总体设计方法，针对剪力键、临时预应力、墩梁锚固等关键结构设计开展了探索研究[7]。李伟超采用有限元软件ABAQUS对试验简支梁进行数值模拟，对接缝截面附近混凝土的应力状态进行了分析[8]，并提出确保胶拼结构质量的相关建议。闫泽宇研究了节段预制拼装UHPC梁胶接缝受力行为，提出UHPC单键齿胶接缝抗剪承载力远高于相同截面尺寸平接胶接缝的抗剪承载力[9]。而针对节段胶拼简支梁施工过程中受力性能的相关研究鲜有报道，施工过程中架桥机和主梁通过吊杆连接，架桥机和主梁为组合结构，吊装过程中架桥机对梁段起支撑作用，张拉过程中，梁体上缘的压应力较小，由于架桥机所恢复的变形值远小于吊梁阶段的变形值，故预应力张拉过程中吊杆对梁体存在向上的拉力，可能使梁体上缘出现拉应力，若梁体上缘开裂，对胶缝和梁体耐久性会产生不可逆的影响。拉应力与架桥机的刚度有直接关系，不同的架桥机刚度影响预应力张拉过程中的架桥机上拱值和吊杆的残余张力，因此针对不同的架桥机刚度需要在拆吊杆前张拉相应的预应力值。本文以48 m节段胶拼简支梁桥施工为工程背景，分析架桥机刚度对节段胶拼简支梁预应力张拉量的影响，并对吊杆拆除前预应力张拉量的确定方法展开研究。

2 工程概况

盐通铁路通张段工程长江大桥南引桥紧邻长江且墩高在50 m以上，大风等恶劣条件较多，无法采用支架法施工，且在墩高较高的情况下如采用32 m简支梁，由于架设设备和结构跨度等因素并不经济，故采用48 m节段预制胶接架桥机拼装简支箱梁[10]。

梁体为单箱单室等高预应力混凝土简支箱梁，梁体采用C60混凝土，梁顶宽12.2 m、底宽6.2 m，梁高为4.0 m。跨中截面顶板厚0.32 m、底板厚0.35 m，腹板厚0.5 m；支点附近顶板厚0.406 m、底板厚0.687 m，腹板厚0.769 m。简支梁结构如图1、图2所示[11]。箱梁纵向预应力钢束采用15-7ϕ5钢绞线，横截面布置如图3所示。设计张拉顺序为N4-N7-N3-N8-N5-N6-N2-N1。

图1 48 m简支梁立面(单位:mm)

图2 跨中/支点横截面(单位:mm)

图3 预应力束布置

箱梁节段选用长线短线结合匹配法进行预制，采用架桥机吊装各梁段并精准定位后进行涂胶。涂胶后张拉临时预应力确保截面上有0.30～0.60 MPa的压应力，然后张拉永久预应力、灌浆锚固后拆除架桥机。48 m简支梁采用TJ1600型架梁机节段拼装施工。由于桥墩较高、风荷载较大，架桥机主梁采用桁架结构，以减少风荷载的影响。架桥机主要由主框架、1～4号支腿、1台主天车、1台辅助天车、吊挂、附属结构、液压系统、电气系统等部分组成[12]。架桥机结构构造如图4所示。

图4 架桥机结构(单位:mm)

3 有限元分析模型

综合考虑架桥机、吊杆、梁体共同作用建立简支梁胶拼施工全过程仿真分析有限元模型。架桥机杆件和节段胶拼简支梁采用空间梁单元模拟，吊杆采用空间桁架单元模拟，胶缝采用长度较小的梁单元模拟，胶缝单元在涂胶阶段激活。有限元模型包含1 071个节点，2 490个单元。整体模型按照现场施工顺序分为架桥机拼装、吊装梁段、涂胶、按设计顺序逐束张拉钢束、拆除吊杆、拆除架桥机等施工阶段，整体有限元模型如图5所示。

图5 48 m简支梁＋架桥机整体有限元模型

在架桥机刚度不同条件下，张拉过程中吊杆作用在梁体上的力也不同，故对架桥机刚度进行调整，分析架桥机刚度对节段胶拼简支梁预应力钢束逐束张拉过程中梁体受力影响，刚度分别取现场架桥机刚度的10%、20%、30%…100%、200%、300%…1 000%。

4 分析结果

由于风荷载引起的动力作用可能会在胶缝处引起拉应力，故张拉过程中其控制条件为胶缝处压应力不得小于0.5 MPa；考虑到临时预应力在永久预应力张拉后拆除，故张拉过程中不得出现拉应力，且梁体下缘的压应力小于20 MPa。

为表达更清晰，分别列出架桥机刚度折减和刚度增加两种情况下的梁体上缘应力，如图6所示(应力以受拉为正、受压为负；刚度比为架桥机计算刚度/实际刚度)。

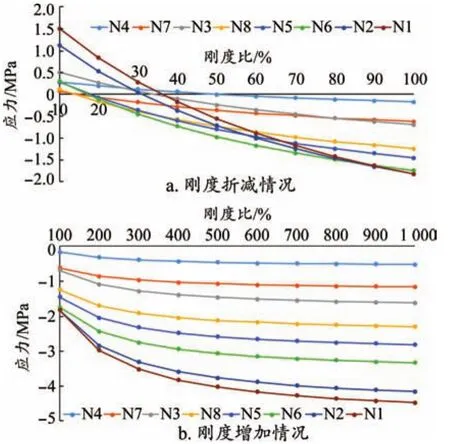
图6 梁体上缘应力

梁体下缘应力如图7所示。

图7 梁体下缘应力

可以看出:

(1)随着架桥机刚度增加，在张拉同一钢束的情况下，梁体上缘压应力逐渐增加，在刚度比较小时变化趋势较大，刚度比大于4倍以上时，变化趋于平缓。

(2)架桥机刚度较小时，上缘应力部分出现拉应力，在现场实际架桥机60%刚度以上情况下，梁体上缘基本处于受压状态。

(3)在刚度比小于70%的情况下，张拉N1钢束时，上缘压应力减小；在刚度比大于100%之后，梁体上缘压应力随着钢束张拉数量的增加而增大。

(4)在刚度比小于70%的情况下，张拉N1钢束时梁体下缘压应力大于20 MPa，90%刚度比时的下缘压应力为19.1 MPa；考虑临时预应力的作用，也同样接近20 MPa限值。故架桥机刚度降低对梁体下缘应力影响较大。

(5)现场实际采用的架桥机梁体上缘未出现拉应力且下缘压应力小于20 MPa，既经济又保证了结构承载力，说明架桥机设计合理。

综上，在架桥机悬吊梁体张拉预应力阶段，为避免梁体截面上缘出现拉应力而导致梁体、胶缝开裂及下缘压应力超限，可适当增加架桥机刚度。

5 拆吊杆前钢束张拉量确定方法

张拉过程中采用两种方案控制预应力张拉量和梁体应力。

5.1 实时放松吊杆方案

张拉过程中采用位移控制，建立仅考虑施工阶段的模型，分析跨中在自重和预应力共同作用下的位移为＋28.3 mm，故张拉过程中按照张拉钢束数量分批控制梁体上拱值，张拉钢束数量按总数的20%、40%、…100%进行控制，对应的梁体上拱控制值按张拉钢束百分比取值。在张拉过程中分批次对梁体标高测点进行控制性测量，若超过该分级上拱限值时需实时放松吊杆，放松量为实测变形值－本级控制值。

5.2 一次性拆除吊杆方案

本方案需要基于精确的有限元计算，鉴于建立架桥机和箱梁的组合模型较为繁琐，故建立两种简化的有限元模型进行分析。

(1)模型一:自重由架桥机承担。该模型不考虑梁体结构自重，梁体自重全部由架桥机承担，不考虑张拉预应力过程中梁体上拱对架桥机产生的卸载作用。在预应力作用下，主要控制梁体上缘应力，在考虑预应力产生的上拱造成架桥机卸载部分自重由梁体承担后，梁体上缘实际压应力将大于计算值。由于未考虑自重作用，混凝土不出现拉应力的限值可适当放宽，根据有关文献，施工过程中混凝土最大拉应力不得超过0.7fct，可保证梁体上缘不开裂。

(2)模型二:自重完全由预应力承担。该模型不考虑架桥机作用，按设计顺序张拉预应力钢束，分析各张拉阶段梁体下缘应力。在拆除吊杆之前，梁体下缘不得出现拉应力且需有一定的压应力储备。

对比实时放松吊杆方案和一次性拆除吊杆方案，前者较适合节段胶拼简支梁桥的预应力张拉过程控制，但放松吊杆需按从跨中到支点以抛物线的分布形式进行。分级较多的情况下，现场工作量较大，施工工艺相对复杂。一次性拆除吊杆方案在进行有限元分析时工作量相对较大，但施工过程相对简单，放松吊杆时也可留有余地，不完全拆除吊杆可为施工过程提供安全保障。

本桥按照一次性拆除吊杆方案进行施工，表1为两种模型下各张拉阶段应力状态。

表1 两种模型张拉阶段梁体应力分析结果 MPa

由表1可知，模型一在张拉至N6钢束之前梁体上缘拉应力变化不大，均小于1.0 MPa，且实际张拉过程中自重会逐渐施加于结构之上，所以实际结构中不会出现模型一中的拉应力。模型二在张拉到N8后下缘才有一定的压应力储备。故实际施工时可选择张拉完成N8、N5或N6后拆除吊杆三个方案，考虑到张拉到N6后上缘应力变化不大，且结构有较大承载力，故可选择N6张拉完成后拆除吊杆。

6 结论

本文对48 m节段胶拼简支梁桥预应力张拉过程中的梁体应力进行研究，分析架桥机刚度对张拉过程中梁体上下缘应力的影响。根据分析结果，得出结论如下:

(1)架桥机刚度对张拉过程中的梁体应力有一定影响，在架桥机刚度较小的情况下，梁体上缘出现较大拉应力，下缘出现了较大的压应力。建议适当增加架桥机刚度以提高节段胶拼简支梁施工质量，确保胶缝强度。

(2)本桥节段拼装过程中采用的架桥机结构合理，刚度适宜，从分析结果看，本桥在拼装过程中梁体上缘一直处于受压状态且下缘压应力未超限值。

(3)提出实时放松吊杆和一次性拆除吊杆方案，并针对一次性拆除吊杆方案提出两种分析模型来保证节段拼装过程中的梁体上下缘应力不超过规范限值。

(4)研究一次性拆除吊杆方案预应力张拉过程中两种模型梁体应力变化规律，并对比分析拆除吊杆前的预应力张拉量确定方法，避免了梁体及胶接缝开裂，可为后续节段胶拼简支梁桥设计和施工提供参考依据。