用于流致振动发电的直线电机设计及优化

邹琳， 陶凡， 徐汉斌， 刘健， 闫豫龙

(武汉理工大学机电工程学院， 武汉 430070)

流致振动是指流体流经固体时会对固体表面施加交替相间的流体力使得固体发生往复运动，而固体的往复运动又会改变流体流态进而改变作用于固体表面的流体力[1]。近年来随着研究的不断深入，学者们[2-3]发现流致振动中的能量可以加以利用来开发新能源。早期的流致振动能量转换装置[4]多采用旋转电机，需要将结构流致振动所产生的位移通过齿轮齿条传动装置带动发电机动子旋转进而产生电能，完成能量转换。谭俊哲等[5]考虑将直线发电机与流致振动相结合，简化能量转换过程进而提高效率。

考虑到结构发生流致振动时做近直线运动的特点，如果采用旋转电机，传动过程存在较大的能量损耗。因此，现设计一个直线电机来进行能量转换，结构发生流致振动时可以直接带动直线电机往复运转来发电，有助于减小传动装置的能量损耗。

Halbach阵列是一种新型的永磁体排列形式[6]，通过合理调整永磁体充磁方向来提高磁场强度，文献[7-8]通过引入Halbach阵列来优化电机性能，优化后电机气隙磁密正弦度高，电磁力波动小、漏磁少等优点。借助电磁场有限元软件对所设计的直线发电机进行仿真分析，首先通过优化Halbach阵列、永磁体厚度和齿部结构来优化感应电动势，另外采用一种L形辅助齿结构来减小齿槽定位力波动幅值，最后分析所设计的直线电机的负载特性。

1 圆筒形永磁直线发电机结构

直线电机采用圆筒形、短定子长动子结构，具有高效率性的同时，可以减小内阻降低后续整流的难度。动子由动子铁芯和永磁体阵列组成，定子由定子铁芯和感应线圈组成，其结构如图1所示。

直线电机的极数和槽数组合比较灵活，但合理选择极槽数可以起到降低定位力的效果。根据文献[9]，周期数Np与极数、槽数的关系为

(1)

式(1)中：GCD(Ns,2p)为槽数Ns与极数2p的最大公约数,周期数越大，齿槽力幅值越小[10]，本文中采用9极10槽的结构可以降低定位力。

所设计的圆筒形直线电机可以看成图2所示的二维仿真模型旋转得到，分析发电机的二维模型可以简化计算。

进行瞬态场仿真时，由于气隙磁场变化率比较大，考虑对气隙进行多层剖分，具体网格剖分原则为气隙处网格尺寸最小，其次是运动区域，然后线圈部分，其他部分都是初始网格大小的一半，圆筒直线电机网格划分效果如图3所示。

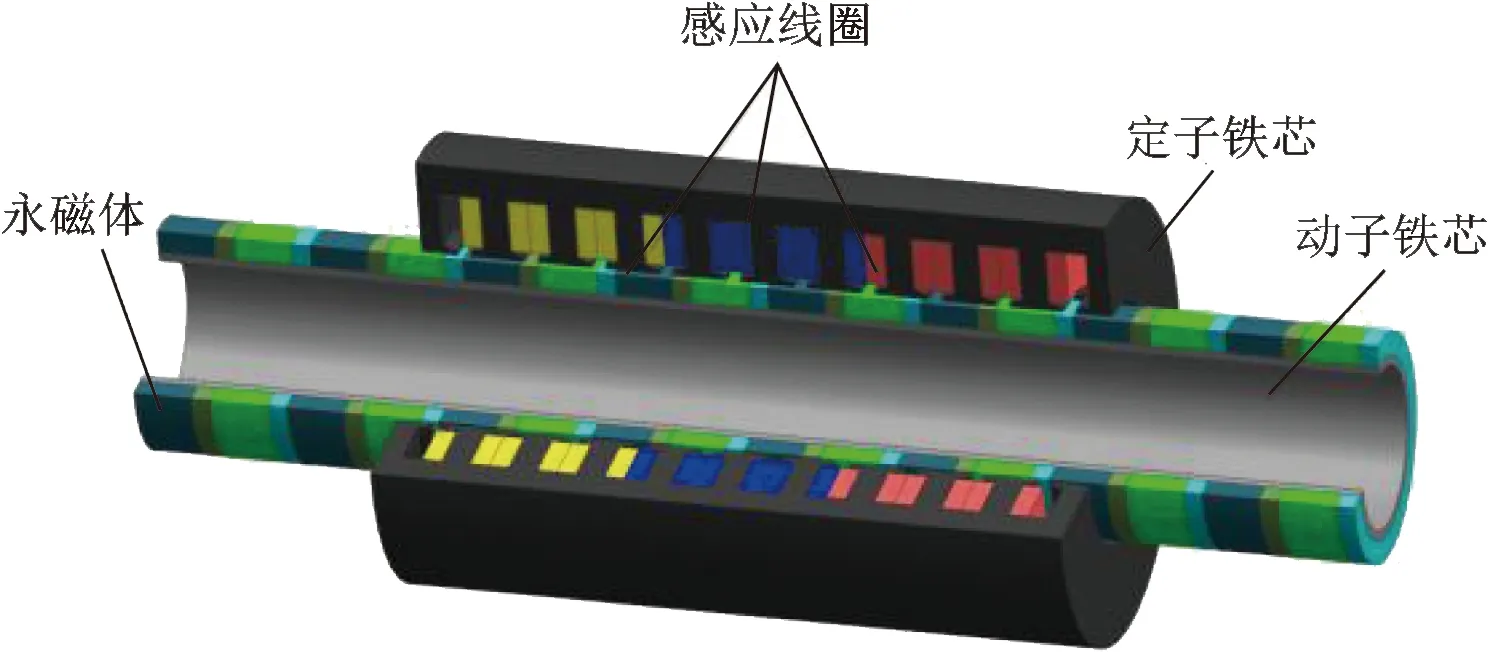
图1 圆筒形永磁直线发电机结构示意图Fig.1 Schematic diagram of cylindrical permanent magnet linear generator structure

图2 圆筒直线电机二维仿真模型Fig.2 Two-dimensional simulation model of cylindrical linear motor

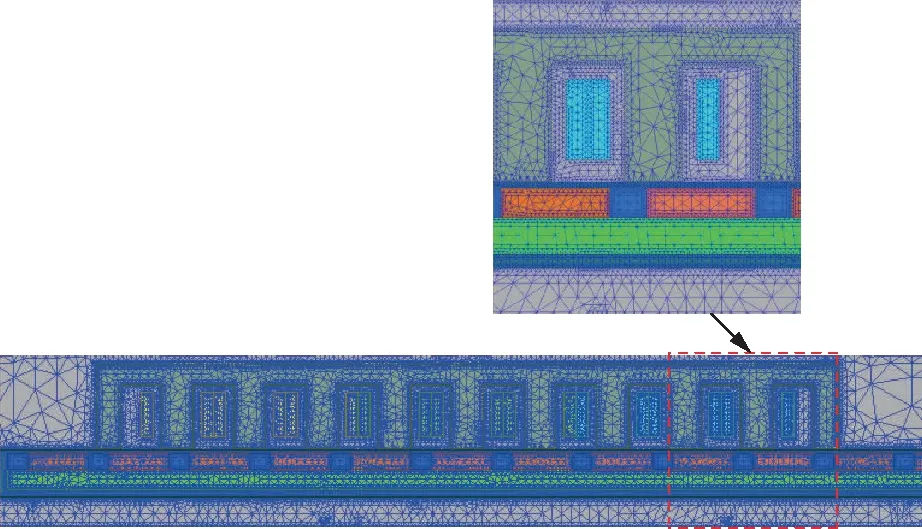
图3 直线电机网格划分Fig.3 Grid of linear motor

2 空载感应电动势优化

2.1 永磁体尺寸优化

在保持直线电机定子尺寸以及极距值不变的情况下，分析径向永磁体长度τr和永磁体厚度ht对电机空载感应电动势幅值E的影响，τr、ht的变化范围分别为12～18 mm和2～6 mm，得到空载感应电动势幅值的变化趋势如表1所示。

由表1可知，空载感应电动势幅值随着径向永磁体长度及永磁体厚度的增加而呈上升趋势，但当径向充磁长度超过16 mm或者永磁体厚度超过4 mm之后，感应电动势增长速度明显变慢。其原因可能是，铁芯材料饱和程度加深，从而导致感应电动势增长变慢[11]。

电机空载感应电动势的波形畸变率大小表示波形偏离正弦性的程度，计算公式[12]为

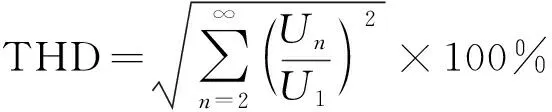
(2)

式(2)中：THD表示畸变率；Un表示n次谐波的有效值；U1表示基波电压的有效值。

图4所示为畸变率的变化规律。从图4可以看出，随着永磁体厚度和径向充磁长度的变化，电机空载感应电动势的畸变率有较大的波动。当永磁体厚度处于2～4 mm、径向充磁长度处于12～14 mm时，总谐波畸变率较小，而径向充磁长度超过16 mm之后，畸变率基本超过10%。综合考虑取永磁体长度3～4 mm，而径向充磁长度取14～15 mm，可以保证畸变率较小的同时感应电动势较大。

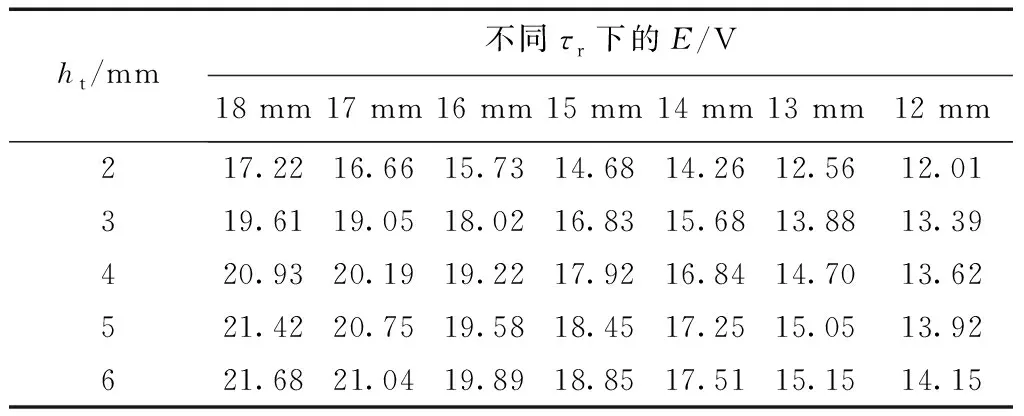
表1 空载感应电动势幅值随径向永磁体长度及 永磁体厚度变化趋势Table 1 Variation trend of no-load induced electromotive force amplitude with length and thickness of radial permanent magnet

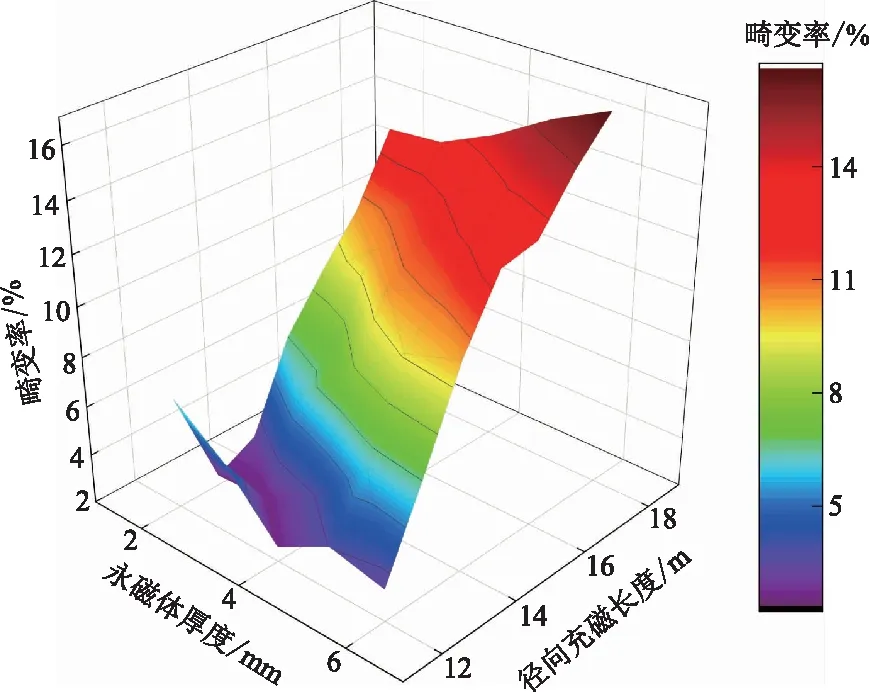
图4 畸变率随径向充磁长度及永磁体厚度变化规律Fig.4 Variation curve of THD with radial magnetization length and permanent magnet thickness

2.2 初级齿部优化

利用Maxwell的参数化分析功能，保证二维直线电机仿真模型除齿宽外的其他尺寸固定的条件下，来分析初级齿宽对直线电机空载感应电动势的影响规律。初级齿宽的范围为4～12 mm，步长为1 mm，得到其感应电动势幅值和畸变率如图5所示。

从图5中可以看出，空载感应电动势的幅值随着齿宽的增加而增加，当初级齿宽为4～8 mm时，感应电动势的幅值上升较快，齿宽超过8 mm后，感应电动势增长明显变慢。与此同时，观察空载感应电动势的谐波畸变率可以发现，波畸变率随着齿宽的增加而逐渐减小，当初级齿宽处于4～8 mm的范围时，畸变率均超过5%，此时波形畸变较严重，尤其当齿宽等于4 mm时，畸变率超过了10%。这说明，此时初级齿部铁芯饱和严重，而且永磁体之间漏磁较大，感应电动势幅值下降。当感应电动势幅值和畸变率在齿宽大于8 mm之后，都逐渐达到最优值，但考虑到槽内绕组需要一定的空间，齿宽不应过大。综合考虑以上因素后，本文中选取齿宽为8 mm。

图5 感应电动势及畸变率随齿宽变化规律Fig.5 The law of induced electromotive force and THD change with tooth width

在齿宽保持不变的条件下改变槽深，发现感应电动势大小及波形几乎不发生变化。为取较大的槽内面积，本文取槽深为16 mm，每槽的线圈匝数为120，经计算槽满率为0.802。

2.3 优化前后结果对比

使用优化后的尺寸在Maxwell中建立圆筒直线电机仿真模型，图6、图7所示为该直线电机优化前后的定子处磁感线图及气隙处磁通密度变化曲线，从图中可以看出来优化后产生的气隙磁通密度曲线中谐波含量更少，而且磁通密度更大，更有助于能量转换过程发电量的产生。空载感应电动势的变化进一步支撑了上述观点，从图8中可以发现，优化后空载感应电动势幅值由11.9 V提高到19.4 V，同时畸变率也有了较大的降低，满足畸变率小于5%的设计要求。

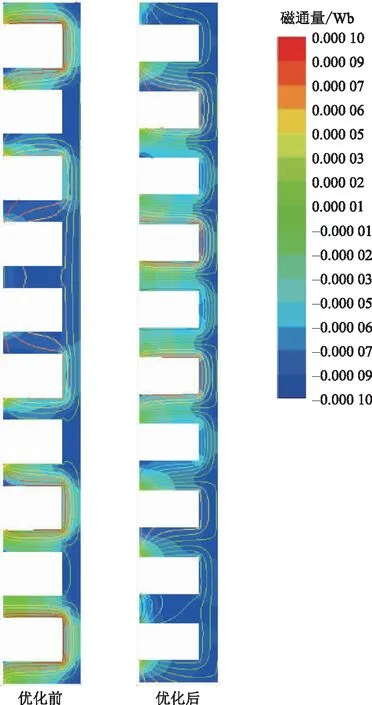
图6 优化前后直线电机定子的磁感线图Fig.6 The magnetic line diagram of linear motor stator before and after optimization

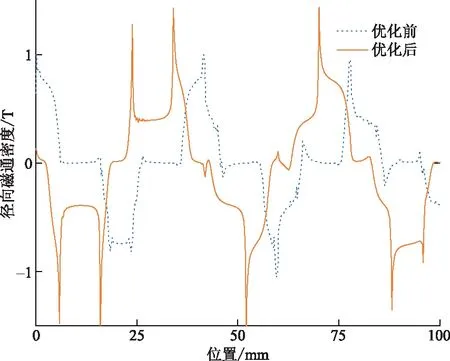
图7 优化前后径向磁通密度曲线Fig.7 The radial magnetic flux density curve before and after optimization

图8 优化前后的空载感应电动势波形对比Fig.8 Comparison of no-load induced electromotive force waveforms before and after optimization

3 定位力优化

由于边端效应和齿槽效应的存在，永磁直线电机存在固有的边端力和齿槽力，合称为定位力[13]。定位力可能会影响流致振动发电系统的稳定性，同时还会影响发电机的输出性能。

有学者提出调整边端齿的宽度和高度[14]、调整定子长度[15]、提出凸定子的结构[16]来减小定位力。参考凸定子结构，现提出一种L形辅助齿结构，通过调整辅助齿的四个参数，既可以达到调整边端齿的长度和宽度的效果，又可以调整定子长度，既达到了减小定位力的目的，还可以减小电机定子的质量和体积。采用有限元法和Taguchi优化方法通过优化辅助齿的几何尺寸来达到减小定位力的目的，所设计的L形辅助齿结构示意图如图9所示。

本文将减小定位力看做Taguchi法的优化目标，将影响定位力大小的参数定义为因子，包括辅助齿1的宽度a和高度d，辅助齿2的宽度b和高度c等可控变量。本文在因子初值附近取4个水平如表2所示。

本文中因子为4个而每个因子有4个水平，想要得到每个控制因子的最优水平组合，一共需要对有限元模型计算44=256次，而采用Taguchi 法仅需16次试验，将因子水平组合输入直线电机仿真模型，可以得到表3所示的正交试验和定位力表，其中定位力为平均定位力。

为分析在不同水平下因子对圆筒直线电机定位力的影响，采用均值和信噪比对仿真结果进行分析(表4、表5)。均值表示每个控制因子水平组合的平均响应，计算公式为

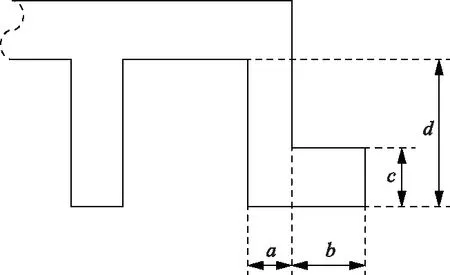
图9 L形辅助齿示意图Fig.9 Schematic diagram of L-shaped auxiliary tooth

表2 不同因子的水平分布表Table 2 Horizontal distribution table of different factors

(3)

式(3)中：α为因子；i为因子水平；m为因子水平内试验次数。

而信噪比是稳健性的度量，为达到定位力最小化的目标，采用望小信噪比SNR，计算公式为

(4)

为了分析不同因子的重要性，考虑使用最大差值法，来计算定位力均值Dave与信噪比的最大差值Dsn，然后比较所计算的差值大小，差值越大则表明该因子重要性也就越高，计算公式为

表3 正交试验表与仿真结果Table 3 Orthogonal test table and simulation results

表4 各因子不同水平下的定位力均值Table 4 The average positioning force of each factor at different levels

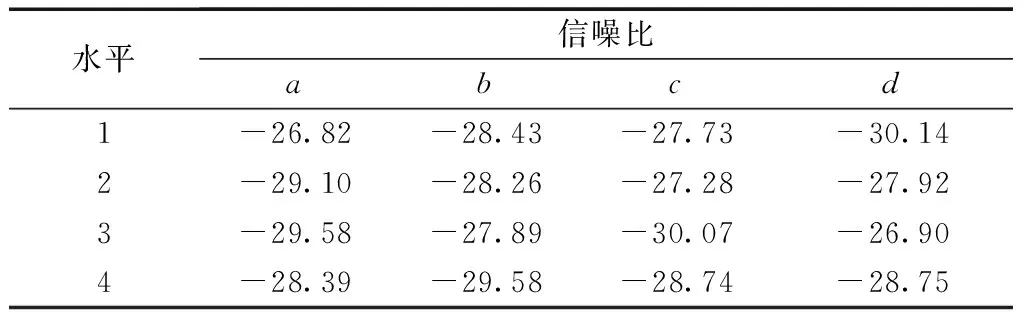
表5 各因子不同水平下的信噪比Table 5 Signal-to-noise ratio of each factor at different levels

(5)

计算结果如表6所示。分析表6可知，本文中各因子对定位力均值和信噪比的重要性由强到弱的顺序为d、a、c、b。综合以上分析，通过Taguchi方法所确定的L形辅助齿最优参数组合为d(3)、a(1)、c(2)、b(2)，其对应的数值分别为15、5、6、4，可以达到定位力最小的结果。

将所得最优参数组合输入直线电机仿真模型中，可以得到优化后的定位力，如图10所示。优化后定位力显著减小，定位力幅值由72 N减小到30 N，降低了约58%，也进一步证明了此方法在电机定位力优化中的可行性。

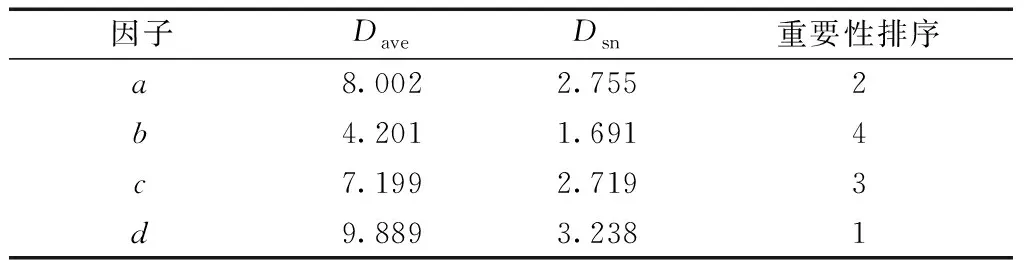
表6 各因子对定位力和信噪比的重要性排序Table 6 The importance of each factor to positioning power and signal-to-noise ratio

图10 优化前后的定位力波形对比Fig.10 Comparison of positioning force before and after optimization

4 负载特性分析

设定动子的运动速度为匀速0.6 m/s，计算直线电机在不同的负载电阻下的电压幅值与电流幅值如图11所示。

从图11可以看出，输出电压随着负载电阻值的增大而增大，而输出电流正好相反，随着负载电阻值的增大而逐渐减小。当负载电阻超过20 Ω后，输出电压幅值基本不发生变化，而输出电流仍会出现较大幅度的下降。

图11 不同的负载电阻下的电压幅值与电流幅值Fig.11 Voltage amplitude and current amplitude under different load resistance

直线电机输出功率可以由电机每相输出端电压的有效值和电流有效值计算得出，公式为

Pout=UaIa+UbIb+UcIc

(6)

绕组铜耗计算公式为

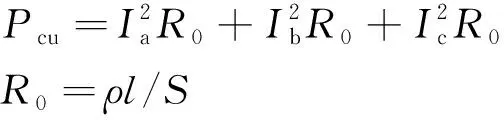
(7)

式中：Pout为输出功率；Pcu为铜耗；Ua、Ub、Uc与Ia、Ib、Ic为电机每相的电压与电流；R0为电机每相内阻；ρ为铜的电阻率；l为绕组铜线长度；S为导体截面积。

在电机输出端加载对称阻性负载，分别对其在不同负载下的输出功率、总功率、铜耗和效率进行计算，计算结果如图12所示。随着负载电阻增大，电机输出电流减小，电机的铜损急剧减小，虽然输出功率同时也随之减小，但下降幅度要远低于负载损耗，因此电机效率呈上升趋势，当负载电阻超过20 Ω后，发电机效率超过90%。

5 结论

提出一种用于流致振动发电的圆筒型永磁直线发电机。首先以高的空载感应电动势和低的谐波畸变率为优化目标，对永磁体尺寸及定子齿部进行优化设计，最终将空载感应电动势幅值提升了63%，同时谐波畸变率满足小于5%的设计要求；然后结合Taguchi法和有限元法，以L形辅助齿的结构参数为因子，以定位力最小为目标进行优化，仿真结果表明，优化后的定位力与优化前相比降低了58%；最后对直线电机在恒速下不同负载电阻的输出性能进行分析。结果表明，所设计优化的圆筒型永磁直线发电机具有空载感应电动势幅值高、畸变率小，定位力小等优点。

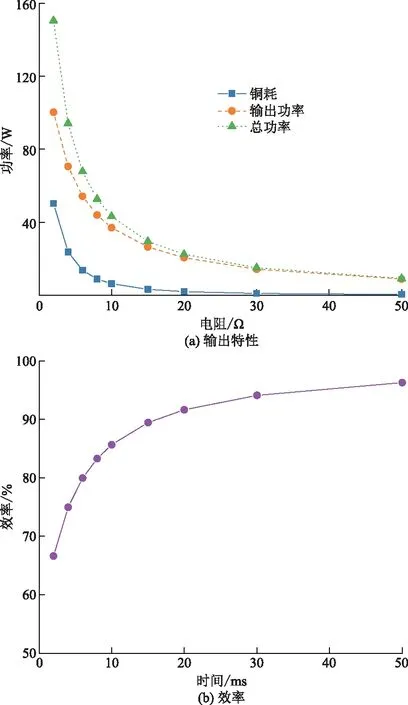
图12 不同负载下的输出特性和效率Fig.12 Output characteristics and efficiency under different loads