基于Robust-M估计的地空频率域电磁探测数据干扰抑制方法
2022-09-30刘长胜白江兰康宁李茁维梁洁周海根阚绍佑
刘长胜, 白江兰, 康宁, 李茁维, 梁洁, 周海根*, 阚绍佑
(1.吉林大学仪器科学与电气工程学院, 长春 130012; 2.地球信息探测仪器教育部重点实验室, 长春 130012)
20世纪70年代初,国外出现了基于地面发射、空中接收的电磁探测系统TURAIR,有较好的分辨率和电阻率鉴别率,应用于探测深度大或地面树林高、地形起伏大等地区[1-2]。地空电磁探测将地面电磁探测与航空电磁探测相结合,早期的地空电磁探测使用直升机搭载探测,成本较高[3];中国较早进行地空电磁探测时,采用无人飞艇搭载电磁接收系统,主要应用于沙漠、海陆交互带以及山区等复杂地形区域,具有探测深度大、分辨率高等优点[4-5]。目前中国无人机行业快速发展,同时也带动了地空电磁探测的发展,使用无人机搭载接收系统进行探测,降低了飞行成本,在空中进行飞行测量,相比较在地面测量,节省了大量的人力物力[6]。
地空电磁探测分为地空时间域电磁探测[7]和地空频率域电磁探测,各有所长,为了综合时域和频域电磁探测方法,简化探测过程,通过时频融合传输方法,同时激发大地产生瞬态和稳态响应,从而提高电磁探测效率[8]。目前中外地空频率域电磁探测主要是对垂直磁场的测量,为了提高探测的准确性,也在不断向着三分量磁场采集的方向发展[9],同时进行姿态数据的采集,对磁场进行姿态校正[10]。地空频率域电磁探测,通过接地导线向大地发射2n序列伪随机波形,在空中采用线圈进行磁场数据采集,在不降低效率的情况下,还能保持一定的分辨率[11]。相比于地面电磁探测,其探测效率高,可快速获得大范围内的地电信息,在复杂地形环境中适用性强[12]。地空频率域电磁探测系统的探测范围和深度与发射频率、发射功率、实际环境噪声、系统参数有关[13]。在复杂地形区域探测时,单源发射导致能量分散,接收端信号微弱,信噪比低,为了进行快速准确探测,Zhou等[14-15]提出了一种双源发射的地空频率域电磁探测方法,提高了探测精度,进而对多源发射的实现提供了理论基础。通过多源发射的实际应用,探测结果显示接收信号明显增强,从而使地空电磁探测更加适用于噪声更强的探测区域。
空中接收电磁系统因受到风向、飞行颠簸等因素的影响,导致数据存在低频运动噪声、姿态噪声、随机噪声、尖峰噪声等,通过小波变换可以有效去除低频运动噪声。朱凯光等[16]研究了基于BP(back propagation)神经网络的线圈姿态校正算法,提高了数据质量。稳健M估计常用于时间域大地电磁探测[17],压制高斯随机噪声和尖峰脉冲噪声[18]。对离群值进行剔除或降权[19],实现对噪声的压制。
地空频率域电磁探测,针对不同噪声采取不同的噪声抑制方法,具有一定的效果[20-21]。但在数据处理中,噪声压制仍然存在很多问题,因受到飞行因素与环境因素的影响,通过无人机搭载线圈进行探测,电磁数据并不平稳,信噪比出现忽高忽低现象,影响数据质量。通过引入Robust-M估计,使信号趋于稳定,提高数据质量。
1 理论基础
1.1 地空频率域电磁探测原理
地空频率域电磁探测系统,如图1所示。
由发射系统通过接地导线向大地发射2n序列伪随机波形,在测区采用无人机搭载线圈,进行数据采集。接收系统采集数据为电信号V,通过数据预处理得到垂直磁场B。即
(1)

图1 地空频率域电磁探测示意图Fig.1 GAFED Schematic diagram
U=-jnBSω=-jnBS·2πf
(2)
(3)
式中:φ为磁通量;n为线圈匝数;S为线圈有效面积;f为发射频率。
1.2 传统时窗选取
传统的数据处理是对数据加窗分段后,进行傅里叶变换,进而得到各个频率下的磁感应强度。数据处理的时窗宽度,通常选取为1 s、2 s、3 s、5 s、10 s、…,通过数据信噪比占比统计结果,对分段时窗宽度进行调整。对野外探测的数据,使用不同时窗宽度进行处理,当时窗为2 s时,其中一条测线的磁感应强度幅值曲线,如图2所示,通过计算测线数据信噪比,统计测区信噪比占比,结果如图3所示。测区具体情况详见3.2节。信噪比为
(4)
式(4)中:SNR为信噪比;S为信号幅值;N为噪声幅值[22]。
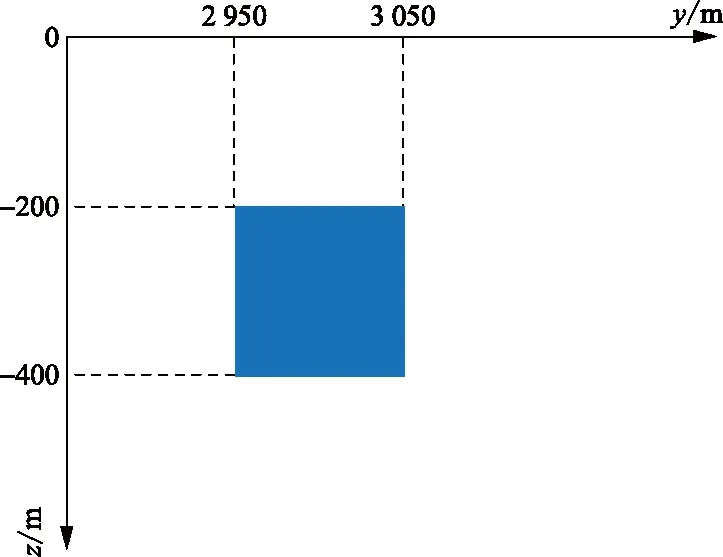
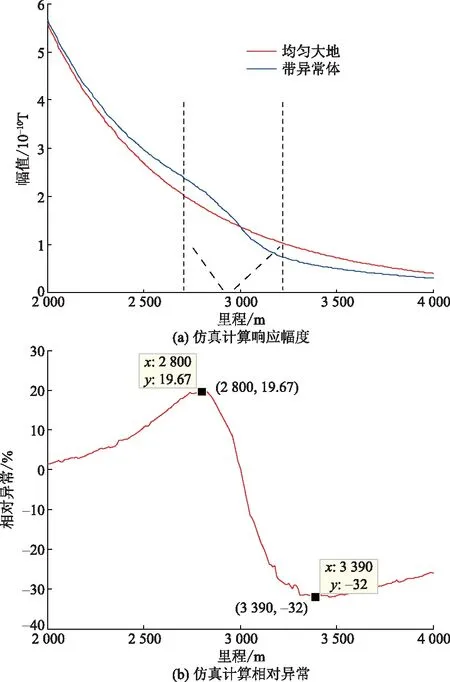
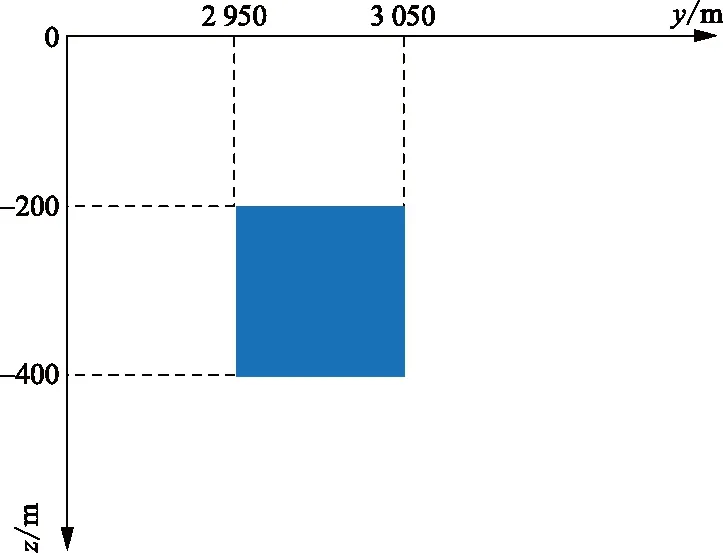
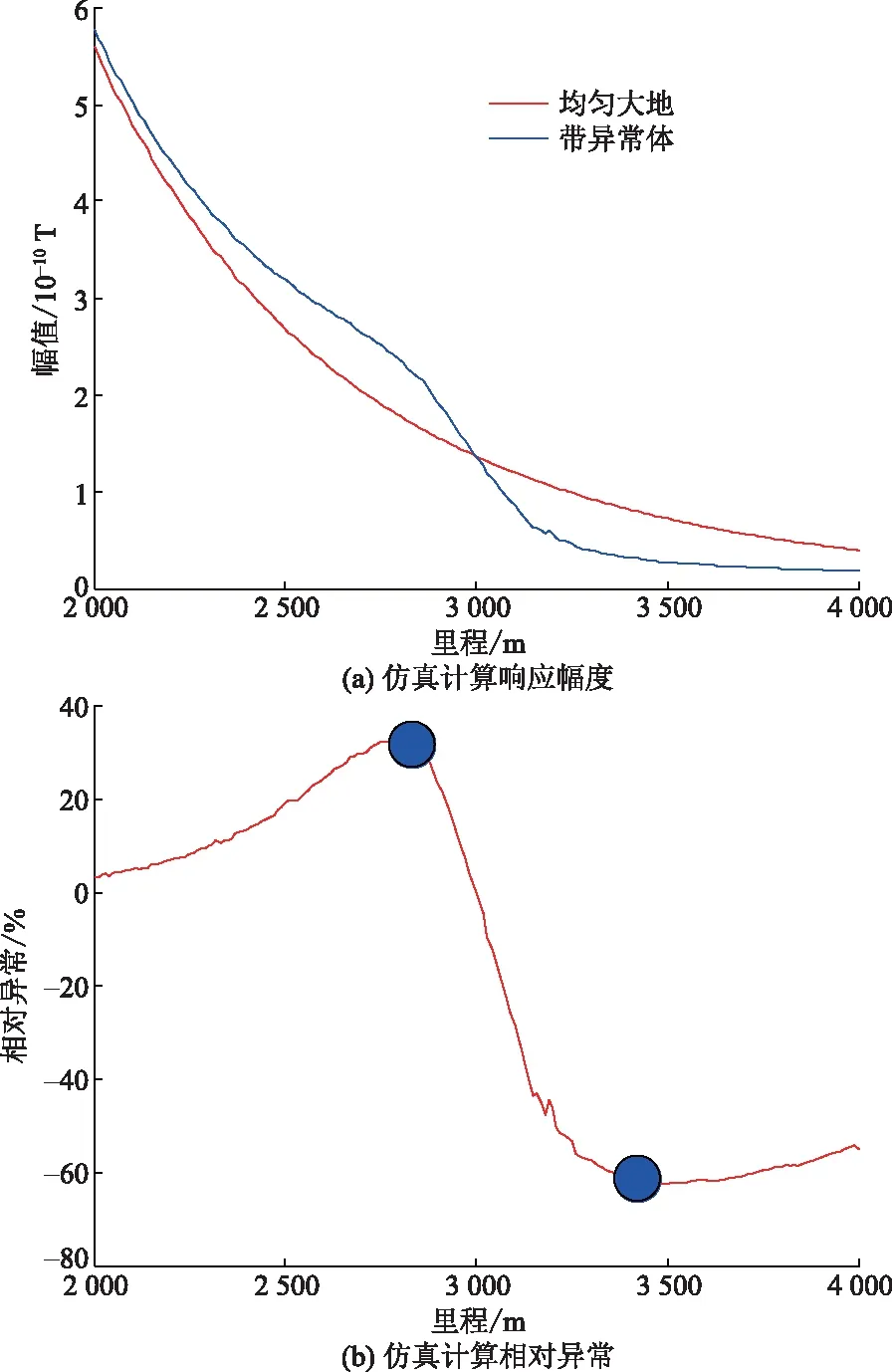
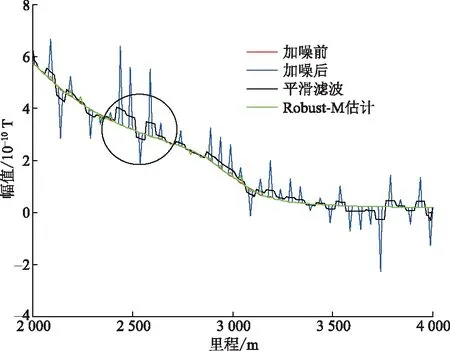
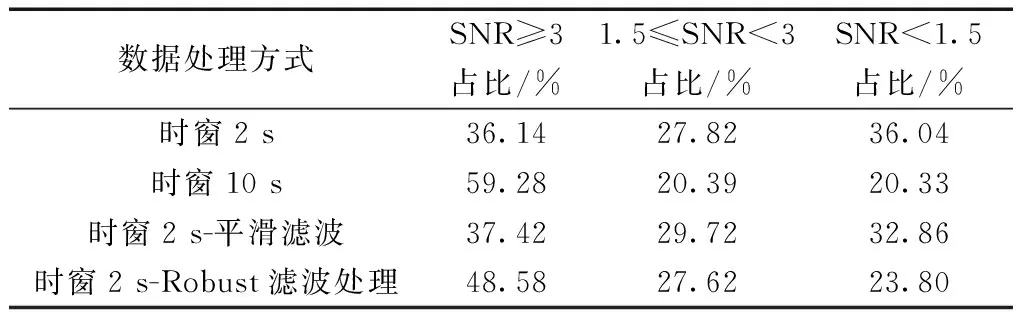
因野外测量,采用无人机搭载探测,而受到环境以及飞行因素的影响,数据存在随机噪声与尖峰噪声,导致信噪比忽高忽低,数据质量差。而时窗宽度与数据信噪比有着直接的关系,由图3可知,随着时窗的不断增大,测区SNR≥3数据占比不断增大,随后趋于稳定;测区1.5 图2 测线信号幅值图Fig.2 Amplitude diagram of line signal 图3 信噪比占比图Fig.3 SNR ratio diagram 通过增大时窗,在一定程度上可以提高数据质量,但同时分辨率有所降低。为在保持一定分辨率的基础上,进一步提高数据质量,本文中引入Robust-M估计方法。 Robust-M估计方法通过对大量数据进行迭代、剔除异常值,从而估计出一个准确值,来代表真实值。大地电磁探测通过在固定地点长时间进行数据采集,使得同一个测点处有大量数据,因此,Robust-M估计方法常用于大地电磁探测。而地空电磁探测采用无人机搭载接收系统进行数据采集,针对单个测点,仅有少量测量数据,并不能直接使用Robust-M估计方法估计真实值,所以需要对Robust-M估计方法进行改进,使其适用于地空频率域电磁探测的数据处理。 Robust-M估计是一种稳健估计法,类似于最大似然估计,用于解决统计问题时[23],通过观测得到原始数据,表达式为 yi=xi+εi,i=1,2,…,m (5) 式(5)中:m为原始数据个数;xi为原始数据的估计真实值;εi为误差序列。 根据最大似然估计准则,选用分段连续的可微凸函数ρ(z),构造目标函数 (6) 为方便求解,定义 (7) 则通过计算,可求得yi的估计真实值xi。 为确定固定大小的异常体对探测数据的影响范围,进行仿真计算。异常体大小为100 m×200 m×1 250 m,埋深200 m,模型的yoz剖面如图4所示,测线沿y轴方向,地空频率域电磁探测仿真计算结果,如图5所示,相对异常大于10%时视为有效异常。通过均匀大地与带异常体仿真计算结果对比分析,可以发现测线方向100 m长的异常体,使异常体前后近500 m范围内的数据受到有效影响。所以在进行数据处理时,将测点前后数据联合,进行测点响应估计。 地空频率域电磁探测通过无人机搭载线圈,进行测线数据采集,数据预处理后,得到磁感应强度为 B(i)=BZ(i)+ε(i) (8) 式(8)中:B(i)为磁感应强度测量值;BZ(i)为磁感应强度预估真实值;ε(i)为误差序列;i为测点数。根据最大似然估计准则,对探测数据进行加窗分段后,构造目标函数 (9) 求解目标函数,当目标函数达到最小时,求解得到的BZ(i)即为估计结果。结合理论分析结果以及大地电磁信号具有连续性的特点,测点数据与测点前后数据具有连贯性,计算包含B(i)在内的B(i-3)~B(i+3)七个测量值的中位数Bimd、标准差Bisd,令 (10) BZ(i)=Bimd+φ(i) (11) 图4 异常体大小及位置Fig.4 Size and location of abnormal body 图5 理论模拟结果Fig.5 Theoretical simulation results 稳健M估计中,φ(x)函数有:中值函数、Huber函数、Hampel函数等多种类型。选用Hampel函数,即 (12) 式(12)中:a、b、c为调节常数[24],定义a=1.2,b=3.5,c=8,通过对测点与测点前后数据应用改进后的方法,估计测点响应真实值。 如图1所示,以发射源为坐标原点,建立空间直角坐标系,x轴沿发射导线方向,z轴垂直向下为正。求解带有边界条件的麦克斯韦方程组,计算空间位置(x,y,z)处的垂直电磁响应。计算公式为 (13) (14) 式中:μ0为真空磁导率;I为发射电流;L为导线长度;rTE为层状大地反射系数;λ为汉克尔积分变量;J1为1阶贝塞尔函数;ε0为真空中的介电常数;f为发射频率。 通过均匀大地磁场表达式,运用MATLAB进行长导线源一维层状介质正演,获得均匀大地垂直磁感应强度。通过Comsol进行均匀大地仿真、带异常体仿真。发射极矩40 000 A·m,测线沿y轴方向,大地电阻率100 Ω·m,异常体电阻率1 Ω·m,异常体大小为100 m×200 m×2 500 m,如图6所示。 图6 异常体位置及大小Fig.6 Size and location of abnormal body 电偶极源仿真计算32 Hz垂直磁场响应幅度和相对异常曲线,如图7所示。通过均匀大地电磁响应与带异常体电磁响应对比,可以发现,测线方向100 m长的异常体将影响异常体前后约500 m范围内的磁场响应,且磁场响应在500 m范围内进行一个缓慢连续的变化;利用MATLAB产生服从正态分布的高斯随机噪声,如图8所示,通过带异常体32 Hz正演数据加噪前后对比图,可以发现,随机噪声、尖峰噪声在短时间内会发生突变,并不符合异常体存在特点。对加噪后的带异常体32 Hz正演数据分别进行平滑滤波与基于Robust-M估计的时窗叠加滤波处理,可以发现,如若在短时间内发生多次突变,平滑滤波处理将会产生一段距离内的数据起伏,与存在异常体的响应特点相近,从而形成假异常,而基于Robust-M估计的时窗叠加滤波方法,结合测点前后数据情况,可以很好地将突变及短时间内的多次突变进行降权处理,以降低突变点的影响,优化数据。 为了验证基于Robust-M估计的时窗叠加滤波方法的有效性,在重庆市城口县进行地空频率域电磁探测,使用无人机搭载单分量线圈进行数据采集。测区概况如图9所示。 图7 理论模拟结果Fig.7 Theoretical simulation results 图8 不同方法对加噪后信号处理结果Fig.8 Different methods to add noise signal processing results 测区位于重庆东北方向329 km,海拔1 500 m。发射电流20 A,接地导线1 000 m。发射频率为32、64、128、256、512、1 024、2 048、4 096、8 192 Hz。共四条测线,测线间隔100 m,长2 800 m。四条测线相互平行,中轴线重复性测量。飞机飞行速度为6 m/s。 图9 测区概况图Fig.9 Survey area overview map 通过图2中32~512 Hz频率下的磁场响应可以看出,因受到飞行因素及外部环境影响,实测信号内存在随机噪声与尖峰噪声,上下波动较大,并不连续,信号质量较差。对测量数据分别进行时窗2 s、时窗10 s、时窗2 s-滤波处理、时窗2 s-Robust-M估计处理,对比应用效果。32 Hz实测数据处理时域结果,如图10所示。因大地的连续性,测得的磁场响应也是连续的,将短时间内出现的突变视为干扰。 通过图10(a)、图10(b)对比,可以发现,随着时窗的增大,分辨率降低,可以有效减少随机噪声、尖峰噪声;通过图10(a)、图10(c)、图10(d)对比,可以发现,在时窗一定的情况下,平滑滤波与Robust-M估计方法对数据均具有一定的优化作用,而平滑滤波根据理论数据处理结果,会因短时间内的多次干扰而造成假异常,Robust-M估计可对异常值进行剔除或降权,时域图与时窗10 s时的时域图更为接近。 分别计算不同处理方法下的测区数据信噪比,统计结果,如表1所示。 通过时窗2 s处理结果与时窗10 s处理结果对比分析,可知,降低分辨率,可以有效减少不合格数据量,提高数据质量。通过时窗2 s处理结果与时窗2 s-平滑滤波处理结果对比分析,可知,平滑滤波处理效果甚微。通过时窗2 s处理结果与时窗2 s-Robust-M估计处理结果对比,可知,基于Robust-M估计的时窗叠加处理方法,可以有效去除随机噪声、尖峰噪声,提高数据质量。 表1 测区信噪比统计结果Table 1 Statistical results of SNR in detection area 图10 32 Hz实测数据处理时域图Fig.10 32 Hz Time domain diagram of measured data processing 地空频率域电磁探测采集数据中,存在众多噪声,需针对不同噪声特点,进行抑制,从而提高数据质量,提高探测的准确性。提出基于Robust-M估计的时窗叠加滤波方法,针对随机噪声、尖峰噪声,具有很好的抑制效果。 (1)通过采用基于Robust-M估计的时窗叠加滤波处理,可以有效剔除数据中过大或过小的异常点。时窗10 s处理结果与时窗2 s-Robust-M估计处理结果对比,可知,SNR<1.5占比几乎一致。通过对比不同处理方法的结果,基于Robust-M估计的时窗叠加滤波方法在保持一定分辨率的基础上,有效提高了数据质量。 (2)虽然Robust-M估计在抑制随机噪声与尖峰噪声方面取得了较好的效果,但是当测点数据存在较大的姿态噪声时,需对电磁数据进行姿态校正后,再应用Robust-M估计滤波方法,从而得到更准确的电磁数据。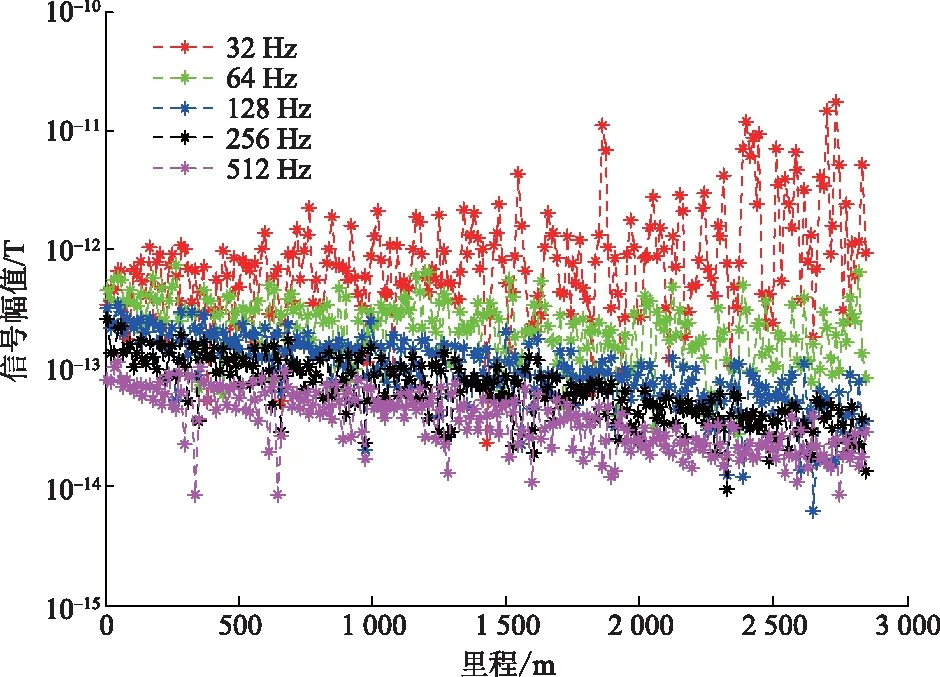

2 基于Robust-M估计的干扰抑制方法
2.1 Robust-M估计算法
2.2 权重的优化设计
3 应用效果测试
3.1 模拟数据测试

3.2 实测数据测试


4 结论与展望
