薄壁箱梁畸变的Galerkin解法*

王兆南 张元海

(兰州交通大学土木工程学院， 兰州 730070)

薄壁箱梁在汽车荷载或其他不对称竖向荷载作用下的畸变效应是非常突出的。为了合理地设计薄壁箱梁，对畸变引起的应力进行准确的计算是非常必要的；同时在薄壁箱梁内部设置横隔板可有效地限制畸变变形，减少箱梁畸变翘曲引起的正应力，从而使得箱形梁在偏心竖向荷载作用下能够受力合理，达到延长桥梁使用期限的目的。薄壁箱梁畸变研究的方法有板元分析法、能量变分法、广义坐标法等[1-2]。对得出的畸变控制微分方程可采用初参数解法，Galerkin解法等求解。其中Galerkin解法可方便地考虑薄壁箱梁内部横隔板设置的数量对畸变效应的影响[3]。Ren等研究了简支箱形梁考虑横隔板剪切变形对畸变的影响[4]。赵甲荐等研究了单箱双室箱梁横隔板的剪切应变能[5]。李运生等进行了钢-混凝土曲线组合箱梁桥横隔板间距的研究[6]。李育楷等研究了横隔板间距对悬挑箱梁畸变的影响[7]。张彦玲等通过有限元研究了横隔板设置对简支单箱双室箱形梁畸变的影响[8]。横隔板的设置对箱梁畸变变形的限制是明显的，能有效地减小箱梁的畸变正应力[9-10]。

畸变控制微分方程的解法较多[11-14]，有适合等截面箱梁畸变研究的初参数法，有适合变截面箱梁畸变研究的纽马克法。弹性地基梁比拟法(BEF法)是解算畸变微分方程的有效方法，然而该方法适合于无限长梁，当箱梁长度在一定范围之内时，初参数法和BEF法在边界附近的计算值存在较大偏差。以上这些方法在考虑箱梁横隔板的影响时，处理较为复杂，没有Galerkin解法方便直观。同时，刘保东等通过波形钢腹板连续刚构桥的扭转畸变试验研究，分析了横隔板对箱梁畸变限制的影响[15]。

本文以箱梁腹板竖向挠度wd为未知量，在改进的箱梁畸变分析理论的基础上，采用能量变分原理建立矩形截面单箱单室薄壁箱梁的畸变控制微分方程，分析以畸变挠度和畸变角为未知量的箱梁畸变扇性坐标、畸变翘曲惯性矩之间的关系。采用Galerkin解法研究箱梁跨内设置的横隔板数量对畸变变形的影响。

1 畸变假定和畸变扇性坐标

等高度简支箱梁，顶板上任意位置作用的偏心竖向均布荷载，均可分解成作用于箱梁各板件连接角点上的反对称荷载P，单位为kN/m，如图1所示。沿梁纵向，从跨中截取单位长的梁段，其顶板、底板和腹板等板件形成一个闭合框架，在此假定[1-2]：

1) 组成框架各板件的横向变形忽略不计，箱形截面的周边不可压缩，横向应变为零。

2) 箱梁发生畸变翘曲时，组成箱形截面的各板件作为各纵向板梁的横截面，分别满足平截面假定。

3) 忽略箱梁各板件厚度对翘曲的影响，剪应力和翘曲正应力沿壁厚均匀分布。

单箱单室矩形截面箱梁截面形式如图1所示，变量d、a1、a2为箱梁框架各板件的宽度；箱梁腹板、底板、顶板(包括悬臂板)的厚度为t1、t2、t4，左、右腹板厚度相等；弹性模量为E，泊松比为μ，反对称荷载P的作用位置如图1所示，分析采用右手坐标系。

图1 单箱单室矩形截面箱梁Fig.1 Single-box single-cell box girders with rectangular sections

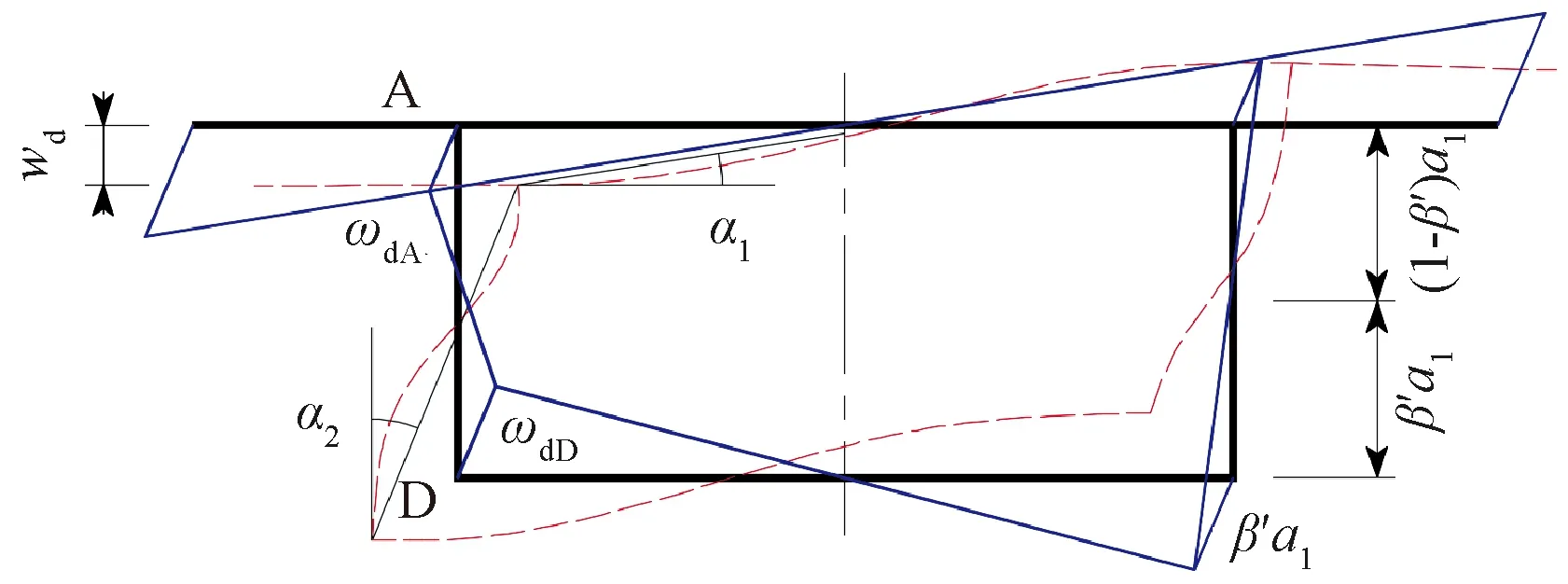
图2 箱梁畸变扇性坐标和畸变特征Fig.2 Distortion sectorial coordinates of box girders and distortion characteristics

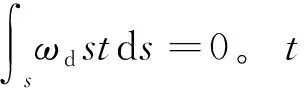
(1)

对此式进行化简并求解β′，解出β′后箱梁横截面上周向各点的畸变扇性坐标数值即可确定。

2 畸变翘曲惯性矩和横向抗弯刚度

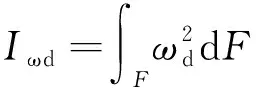
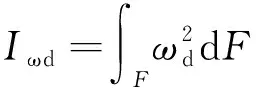
t2a2β′2+t1a1(6β′2-6β′+1)]

(2)

因有β′=β/(1+β)，用β代替β′，则上式变为：

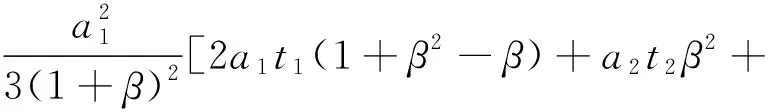
(3)

如以畸变角γd为未知量，推导箱梁畸变翘曲惯性矩Iωd，则角点A的畸变扇性坐标ω′dA为：

(4)

式中：kd为和箱梁截面畸变中心相关的系数[2]。

角点D的畸变扇性坐标ω′dD为：

(5)

这两种未知量对应的畸变扇性坐标在箱梁横截面角点处的数值存在一个比值为a2/4。在此，以畸变扇性坐标ω′dA和ω′dD为基础，推导以畸变角γd为未知量的对应的箱梁畸变翘曲惯性矩Iωd，最后可得Iωd见式(6)，单位为m6。

(6)

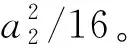
箱梁横向框架抗弯刚度Kd，根据结构力学中杆件矩阵位移法的关于杆件刚度的表达式，可得箱梁框架横向抗弯刚度[3]为：

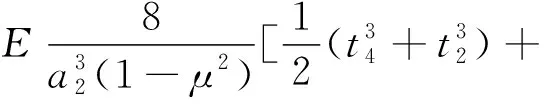
(7)

对文献[16]中的以箱梁腹板挠度为未知量，建立的梯形截面箱梁畸变翘曲惯性矩的计算式进行修正。修正后的箱梁畸变翘曲惯性矩计算式如下所示。

(8)

其中Δ=Δ1+Δ2

3 以wd为未知量的畸变微分方程和解法

(9)

对式(9)进行变分运算后可得：

(10)

方程(10)求解的边界条件为：δw′d(EIωdw″d)=0，δwd(EIωdw‴d)=0。在简支端：wd=0，w″d=0。针对畸变微分方程(10)可采用Galerkin法进行求解，设腹板的竖向位移为：

(11)

式中：l为箱梁梁端横隔板的间距；bk为一常数。

将wd代入式(10)，在等号两端同乘sin(kπz/l)后得到：

(12)

如有P为常量均布荷载，可解出bk=2Pl4/(EIωdk5π5+Kdkπl4)，k=1，2，3，…。因此，简支带有端横隔板的等高度薄壁箱梁的腹板的竖向位移可表示为：

(13)

简支薄壁等高度箱梁，除设置端横隔板以外，箱梁跨内还设置有n道横隔板。此时相邻横隔板的间距为l/(1+n)，设跨内布置了横隔板的箱梁腹板竖向位移wdn为wdn=bknsin[(n+1)πz/l]，如同式(13)得出的过程，则wdn和跨内横隔板数量n之间有如下关系：

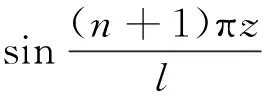
(14)

对应的箱梁跨内横隔板的数量n可取为0、1、2、3等。

4 数值算例

取数值算例，采用本文方法计算箱梁在偏心竖向荷载作用下腹板的竖向挠度，考察增加的横隔板对箱梁畸变变形的影响。

算例1为矩形截面简支箱梁桥，取自文献[3]。计算跨径L=32 m，E=36.5 GPa，μ=0。在箱梁顶板和腹板相接处施加均布线荷载P=2 kN/m，箱梁截面尺寸如图3所示。

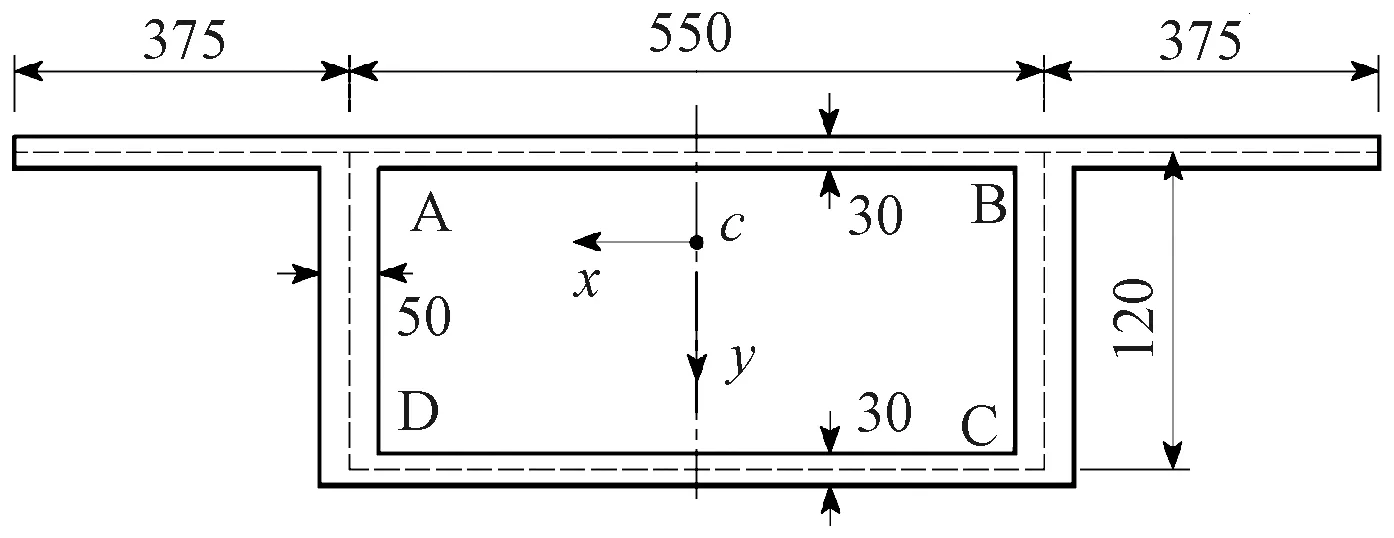
图3 箱梁截面尺寸 cmFig.3 Box girder cross sections

采用本文方法得出的算式，计算得到有端横隔板的简支箱梁畸变参数和跨中截面腹板竖向挠度wd等项目数值如表1所列。采用比拟的弹性地基梁解法(BEF法)得到的箱梁跨中截面腹板竖向挠度为0.029 6 mm，略大于本文方法得出的数值。本文解和文献[3]给出的解相互吻合较好。采用ANSYS软件的Shell 63单元建立箱梁有限元模型，共划分68 520个单元。分析得出的箱梁跨中截面腹板竖向挠度wd为0.035 92 mm，如表1和图4所示。箱梁腹板竖向挠度采用有限元分析得出的值比相关文献数值，其他解析法得出的数值大。

表1 算例1箱梁畸变计算Table 1 Box girder distortion of example 1

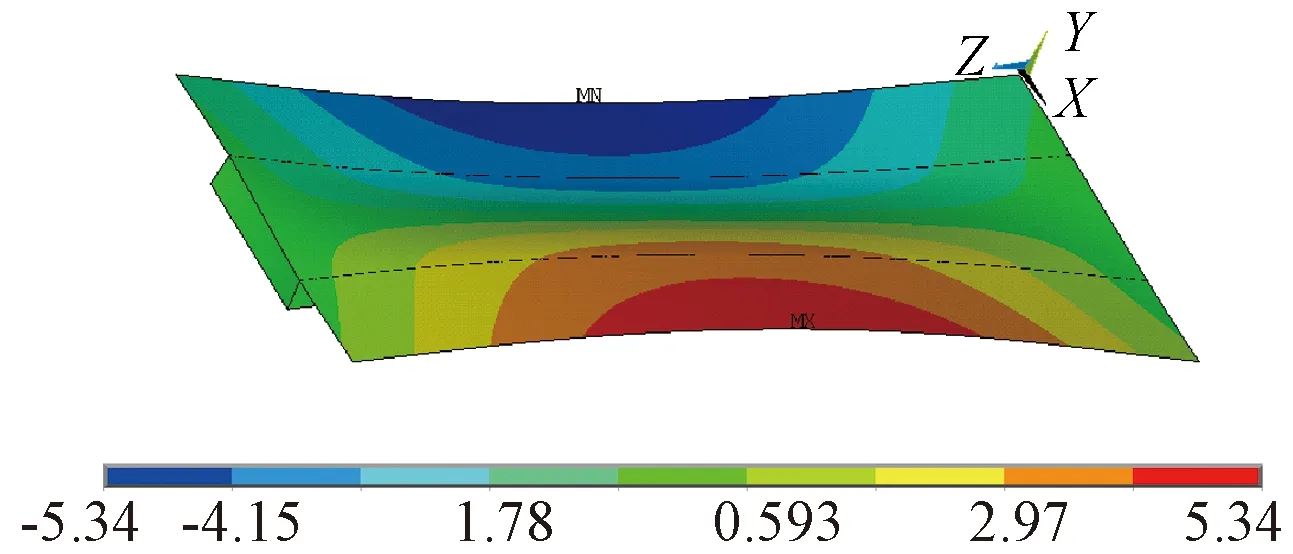
图4 算例1箱梁跨中腹板竖向挠度wd 10-5mFig.4 Vertical deflection at the mid-span web of the box girder in example 1

采用本文Galerkin解法计算简支箱梁跨中截面腹板的挠度和跨内横隔板的数量关系如表2所列。跨内有横隔板的箱梁畸变挠度减小量与跨内无横隔板的箱梁畸变挠度相比较，畸变挠度减小量的数值见表2。

表2 箱梁跨中腹板竖向挠度wdTable 2 Vertical deflection at the mid-span web of the box girder

由表2可见，在简支箱梁设置端横隔板的情况下，箱梁跨内横隔板数量为0时，跨中截面腹板竖向挠度为0.025 89 mm；箱梁跨内设置1道横隔板时，跨中截面腹板竖向挠度为0.005 89 mm，畸变挠度减小量为77.25%；箱梁跨内设置2道横隔板时，畸变挠度减小量为95.48%；跨内设置3道横隔板时，畸变挠度减小量为98.84%。由此可以看出，简支箱梁在端横隔板存在的情况下，在跨内设置1道横隔板时，畸变挠度就可减小到77.25%。若设置3道横隔板，箱梁畸变变形将很小，在偏心竖向荷载作用下箱梁仅可按约束扭转计算偏心效应。即使设置2道横隔板，畸变挠度减小量为95.48%，畸变效应也可忽略。

为直观表达箱梁跨内横隔板数量的增加对简支箱梁跨中截面腹板竖向挠度的影响，现绘出二者的关系，如图5所示。分析得到：箱梁跨内设置较多的横隔板对减小箱梁在偏心竖向荷载作用下的畸变变形限制是有限的，横隔板数量设置较多时还会增加箱梁设计和施工的难度，对简支箱梁跨内横隔板的数量设置不宜过多。

图5 箱梁横隔板数量和腹板挠度关系Fig.5 The relations between the number of diaphragms and deflection of the box girder web

采用Galerkin解法，箱梁横隔板的数量对箱梁畸变变形的影响，在畸变微分方程的解当中得到了直观的体现。采用初参数法时，这一过程较为复杂。采用本文的方法计算箱梁畸变翘曲正应力的数值与其他方法的计算结果是相同的。

算例2取自文献[16]，截面形式如图1所示，简支单箱单室矩形截面箱梁。计算跨径L=40 m，E=31 GPa，μ=0.167，截面尺寸a1=2 m、a2=4 m、d=2 m、t1=0.35 m、t2=0.2 m、t4=0.25 m。通过本文方法，文献[16]给出算式，本文修正后的文献[16]中的算式计算箱梁的畸变效应各参数，结果如表3所示。

采用ANSYS有限元程序的Shell 63单元建立箱梁有限元模型，共划分65 600个单元。分析得出的箱梁跨中截面腹板竖向挠度wd为1.39×10-5m，如图6所示。将箱梁跨中截面顶板和底板角点处的横向弯曲应力提取出来，换算成箱梁框架A、D点的畸变横向弯矩mA、mD如表3所示。

图6 算例2箱梁跨中腹板竖向挠度wd 10-5mFig.6 Vertical deflection at the mid-span web of the box girder in example 2

表3中，有序号①的这一行采用文献[16]的原数据；有序号②的这一行为采用文献[16]中梯形截面箱梁畸变效应计算式得到的数据，其中畸变翘曲惯性矩和文献[16]中矩形截面箱梁的畸变计算式得出的数据不同，箱梁横向框架刚度和文献[16]给出的原数据相同；有序号③的这一行，为对文献[16]相关计算式修订后，及采用本文计算式(8)得出的数据。

采用文献[16]的矩形截面箱梁畸变效应计算式得出的腹板竖向挠度为0.959×10-5m，采用文献[16]的梯形截面箱梁畸变效应计算式得出的数值为1.474×10-5m。通过对文献[16]的相应计算式的修正，得出的腹板竖向挠度为1.497×10-5m，这一数值与本文方法计算的数值吻合良好。采用有限元计算的数值为1.390×10-5m，与本文方法计算值相差仅为6.71%。其他项目数值见表3，框架的畸变横向抗弯刚度，采用各方法得到的数值都相同；畸变翘曲惯性矩数值由于分析采用的方法不同，得到的数值也不相同。

对于箱梁畸变横向弯矩，在算例2中采用两种方法来计算。一种为求出箱梁畸变角或腹板竖向挠度，再通过换算得出箱梁的畸变横向弯矩；一种直接采用框架分析法计算得到箱梁畸变横向弯矩。算例2的箱梁畸变横向弯矩数值如表3所列，可以看出，以箱梁腹板竖向挠度为未知量的畸变效应分析方法，得出的角点A的畸变横向弯矩在数值上都很接近，框架分析法计算的数值较大。

框架分析法对箱梁角点D的畸变横向弯矩计算值和有限元结果较为接近；本文方法计算数值和文献[16]修正后算式的计算结果较吻合，和文献[16]原数据结果相差较大。通过此例的分析，框架分析法和采用箱梁畸变分析理论直接计算箱梁畸变横向弯矩的计算方法得到的结果还是有一定的差异。

5 结束语

1) 矩形截面单箱单室箱梁，采用以腹板竖向挠度wd为未知量的箱梁畸变分析中，箱梁横截面角点处的畸变扇性坐标值和以畸变角为未知量的分析过程得出的数值之比为a2/4，畸变翘曲惯性矩之比则为该值的平方。

2) 通过以腹板挠度为未知量的畸变微分方程采用Galerkin法求解，在设置端横隔板的情况下，跨内设置3道横隔板的时候，箱梁的畸变效应就可忽略不计，可仅按箱梁约束扭转进行偏心效应的分析。设置更多的跨内横隔板对箱梁畸变变形的限制效果不会更明显。

3) 在计算箱梁腹板竖向挠度时，本文方法和相关文献数值、有限元分析结果相互吻合较好。在计算薄壁箱梁畸变横向弯矩时，各方法结果之间有一定的差距，因此待进一步研究分析。