图像可逆数据隐藏技术研究综述
2022-09-30熊祥光樊梦婷陈艺钟思尧
熊祥光, 樊梦婷, 陈艺, 钟思尧
(贵州师范大学大数据与计算机科学学院, 贵阳 550025)
从20世纪40年代中后期的数字化革命开始,经过50多年的发展,人类社会已经步入了信息化社会阶段。自1993年出现了第一个被广泛使用的浏览器(Mosaic网页浏览器),多媒体形式也逐渐多样化,产生了文字、图像、声音等新型多媒体。随着数字媒体技术与网络通信技术的迅速发展,信息的发布和传输也实现了数字化和网络化。网络技术的普及,人们获取信息、传输信息越来越便捷,但由于网络具有开放性、共享性等特点,数字媒体很容易被复制、修改和传播,信息的保密性、真实性、完整性难以得到保障,导致诸如版权侵犯、信息泄露等安全性问题时有发生。
20世纪90年代中期,在信息网络安全、国家安全方面的强烈需求背景下,尤其是出于对网络环境中数字产品的版权保护,信息安全研究领域开展了信息隐藏这一个新的研究方向。信息隐藏作为能够提供信息保护的一种有效技术,受到了众多研究者的广泛关注,已提出多种性能良好的信息隐藏算法。现主要对空域可逆数据隐藏中的经典算法进行介绍和讨论,主要安排如下:首先简要介绍了信息隐藏技术的分类、应用及特性;其次给出了可逆数据隐藏技术的基本框架,总结了可逆数据隐藏算法常用的性能指标;然后分别介绍和讨论了基于差值扩展、直方图平移、预测误差扩展、像素值排序和插值技术的可逆数据隐藏算法;最后对可逆数据隐藏技术的未来发展方向进行了展望。
1 信息隐藏技术
在信息安全领域,传统加密技术研究的是在通信前如何将秘密信息进行特殊编码,以形成未经授权的用户不可识别的密码形式传递,它仅隐藏了秘密信息的内容。然而,信息隐藏(也称为数据隐藏)主要研究的是如何将秘密信息嵌入或隐藏于另一载体(如文本、图像、音频、视频等)中,使第三方难以识别到秘密信息的存在,从而保证其安全性的一门技术,它不仅隐藏了秘密信息的内容,而且还隐藏了秘密信息的存在。
1.1 信息隐藏技术的分类及应用
信息隐藏主要包含数字水印、信息隐写和可逆隐藏三种技术,它们的联系和区别如图1所示。具体来说,数字水印主要关注如何可靠地提取数据,它将鲁棒性视为重中之重,主要应用于多媒体产品的版权保护;信息隐写侧重于数据嵌入行为的不可感知性,它的一个重要应用是隐蔽通信;可逆隐藏不仅可以将嵌入的秘密数据完整地提取出来,而且能无损地恢复原始载体,主要应用于诸如军事、医学图像等需要恢复原始内容的敏感领域[1]。
信息隐藏是一门交叉学科,在计算机、通信、保密学等领域有着广阔的应用前景[2-3]。经过20多年的研究和发展,信息隐藏技术逐渐成熟,常见的应用如图2所示。
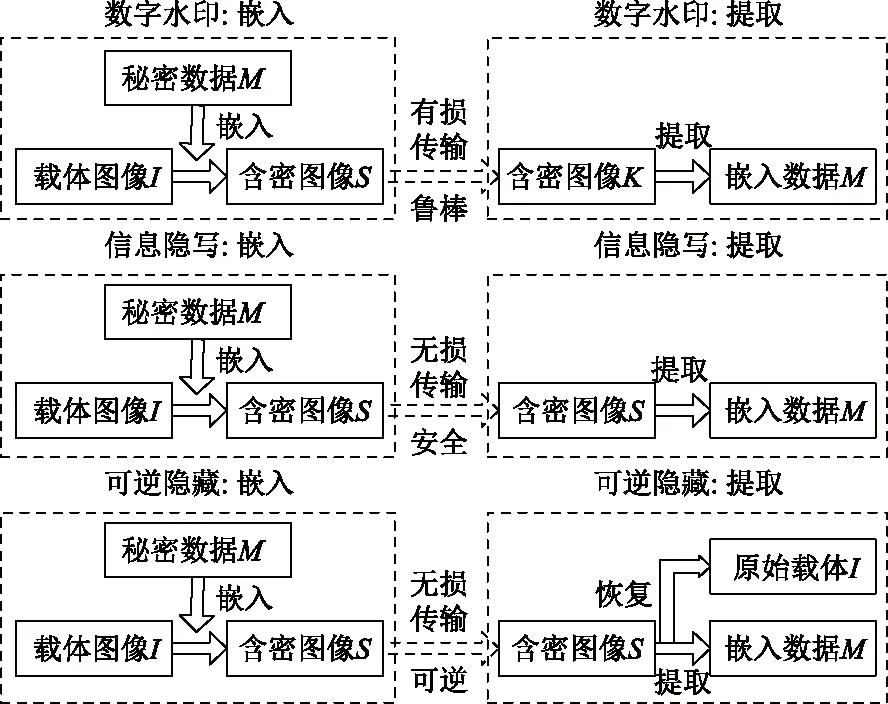
图1 信息隐藏的三大分支Fig.1 Three branches of information hiding technology

图2 信息隐藏技术的应用Fig.2 Application of information hiding technology
1.2 信息隐藏技术的特性
信息隐藏与传统的加密技术有所不同,其目的并不在于限制正常的资料存取,而在于保证隐藏的数据不被侵犯和发现[4]。信息隐藏技术根据目的和技术要求不同应具备如下特性。
(1)透明性或不可感知性:它是信息隐藏技术的基本要求。在原始载体中嵌入秘密数据后,人类视觉系统或听觉系统不能感知到秘密数据的存在。也就是说,嵌入的秘密数据不会给原始载体带来感知上的失真,非法的第三方难以察觉秘密数据的存在。
(2)鲁棒性:在不产生载体质量明显下降的前提下,嵌入的秘密数据不会因载体受到某种攻击而出现丢失,提取的秘密数据仍能识别。
(3)安全性:指数据隐藏算法要有抵抗恶意攻击的能力,能够保证隐藏的秘密数据不会受到破坏。在涉及到加密算法的信息隐藏技术中,要把对秘密数据的保护转换为对密钥的保护,考虑密钥的产生、分发和管理等。
(4)不可检测性:指嵌入秘密数据后的载体与原始载体需具有一致性,非法的第三方无法根据嵌入秘密数据后的载体判断出是否有秘密数据隐藏其中。
(5)自恢复性:承载秘密数据的载体在经过某些操作或变换后可能会受到较大破坏。在原始载体未参与的情况下,仅根据留下的片段数据,仍能有效恢复嵌入数据。目前,大多数信息隐藏算法并不具有该特性。
2 可逆数据隐藏技术
2.1 可逆数据隐藏技术的基本框架
可逆数据隐藏(reversible data hiding,RDH)技术主要包含嵌入过程和提取过程两个阶段,如图3所示。在发送端,首先利用数据嵌入算法将秘密数据M嵌入到原始载体图像I中,然后将嵌入秘密数据后的图像S发送给接收者。在接收端,利用提取算法提取嵌入的秘密数据M,并恢复原始载体图像I。可逆数据隐藏技术的核心是高性能的数据嵌入算法。

图3 RDH一般框架Fig.3 The general framework of RDH
2.2 RDH算法的性能评估
利用数据嵌入算法将秘密数据嵌入到载体中后,为能客观评估嵌入算法的性能,通常采用峰值信噪比(peak signal to noise ratio,PSNR)和嵌入率(bits per pixel,BPP)两个指标,如表1所示。

表1 RDH算法常用的性能评估指标Table 1 Common performance evaluations of RDH algorithm
3 典型的RDH算法
最早的可逆数据隐藏方案由Barton[5]在美国专利中提出。迄今为止,在加密域[6-14]、JPEG压缩域[15-18]和空间域[19-61]中已经提出了许多RDH方案。
空域图像泛指未经明显压缩、保留了自然图像大部分冗余性的图像载体,其主要思想是对像素值进行直接修改。由于具有嵌入容量高、视觉质量好和计算复杂度低等特性,空域图像可逆数据隐藏技术被广泛使用。现有的空域RDH算法主要包含基于无损压缩(lossless compression,LC)的方法[19-21]、差值扩展(difference expansion,DE)[22-30]、直方图平移(histogram shifting,HS)[31-38]、预测误差扩展(prediction error expansion,PEE)[39-44]、像素值排序(pixel value ordering,PVO)[44-49]和插值技术(interpolation technology,IT)[50-57]。
在RDH早期阶段,主要使用的是基于LC的方法,其主要思想是对载体图像进行无损压缩以产生冗余空间,然后利用节省出的空间进行秘密数据嵌入。Fridrich等[19]根据无损压缩的思想,提出了通过对载体图像具有最小冗余的位平面进行压缩以嵌入秘密数据的RDH方案。Celik等[21]提出了一种广义最低有效位(generalized-least significant bit,G-LSB)压缩的RDH方案,提高了嵌入率。由于位平面间具有非常弱的相关性,在一定程度上会限制嵌入容量大小。另外,若直接对载体图像进行压缩也会产生噪声,引入更大的失真,影响图像质量。目前,已很少提出基于LC的RDH方案。
3.1 基于DE的RDH算法
Tian[22]于2003年首次提出基于DE的RDH方案,它将原始载体图像划分为由两个相邻像素组成的像素对以更好利用像素间的相关性,然后通过可逆整数变换扩展两个像素间的差值将1位秘密数据嵌入到像素对中。理论上最大的嵌入率(BPP)为0.5,在嵌入容量和图像质量方面均显著优于基于LC的RDH方案。后来,Alattar[23-25]通过利用向量替代像素对进行差值扩展,提高了BPP。在文献[23]中,将每三个相邻像素视为一个向量,用于嵌入2位秘密数据,理论上最大的BPP为0.67。在文献[24]中,将每四个相邻像素视为一个向量,用于嵌入3位秘密数据,理论上最大的BPP为0.75。文献[25]对这两个算法进行一般化,将每n个相邻像素视为一个向量,用于嵌入n-1位秘密数据,理论上最大的BPP为(n-1)/n。可以看出,n越大,BPP越大,但是,实验发现当n较大时图像质量失真严重。目前,差值扩展(DE)已得到了广泛的研究和发展,典型的改进策略主要包含预测误差扩展[26-27]、自适应预测误差扩展[28]、局部预测误差扩展[29]、最优预测误差扩展[30]等。
给定像素对(x0,x1),假设待嵌入的秘密数据为m,m∈{0,1},差值扩展(DE)的数据嵌入和提取步骤如下。
步骤1计算像素x0和x1的平均值L及差值h,公式为

(1)
h=x1-x0
(2)
步骤2将差值h转换为二进制,然后左移1位,再将1位秘密数据嵌入到h中生成新的差值h′。该过程可表示为:h′=2h+m。
步骤3根据差值h′和平均值L计算嵌入秘密数据后的像素值,公式为
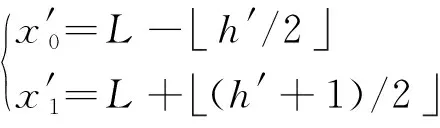
(3)
步骤4提取过程是嵌入过程的逆过程。首先计算含秘密数据像素对(x′0,x′1)的平均值和差值为

(4)
h′=x′1-x′0
(5)
步骤5将h′转换为二进制数,它的最低有效位(least significant bit,LSB)即为嵌入的秘密数据位,该过程可表示为:m=LSB(h′)。


(6)
从上述秘密数据嵌入和提取过程可以看出,DE嵌入方法具有实现简单和计算效率高等特点。理论上,该方法的最大嵌入率为0.5。但是,由于嵌入秘密数据时,可能会出现溢出,若将辅助信息与待嵌入的秘密数据一起嵌入载体,则纯嵌入容量会进一步减小。若要嵌入的容量不高和载体图像较平滑,则采用DE嵌入能取得较好的性能。
3.2 基于HS的RDH算法
除基于DE的RDH算法外,HS是RDH技术中的另一个典型算法。该算法首先生成直方图,然后通过修改生成的直方图实现可逆数据嵌入。下面以Ni等[31]的方案为例,详细描述基于HS的RDH算法的嵌入和提取过程。
3.2.1 Ni等的RDH方案
Ni等[31]于2006年首次提出基于HS的RDH方案。与之前的方案相比,该方案可以有效提高嵌入容量并改善图像质量,其主要思想是先对非峰值点进行平移,然后利用峰值点嵌入秘密数据。在文献[31]中,每个像素值至多修改1,确保嵌入秘密数据后的图像质量始终高于48 dB。然而,由于该方法的数据嵌入容量等于载体图像直方图中峰值点所对应的像素总数,对于直方图比较平坦的载体图像来说,无法找到显著的峰值点,导致嵌入容量和图像质量可能都不太理想。
零点大于峰值点的数据嵌入过程如图4(a)所示。假设零点为a,峰值点为b,且a>b,待嵌入的秘密数据为m,m∈{0,1},基本的数据嵌入和提取步骤如下。
步骤1在原始载体图像I的直方图中,寻找到一个零点a和一个峰值点b。
步骤2根据式(7)进行平移和嵌入秘密数据m,生成嵌入秘密数据后的像素值。
(7)
步骤3提取时,根据嵌入时选择的零点a和峰值点b,提取嵌入的秘密数据m可表示为

(8)
步骤4基于零点a和峰值点b,恢复原始像素值可表示为

(9)
在嵌入秘密数据后的图像S中执行步骤3和步骤4,可准确地提取嵌入的秘密数据和无失真地恢复原始载体图像I。同理,零点小于峰值点的数据嵌入过程如图4(b)所示,其嵌入过程与上述步骤基本相同。
上述基于HS的数据嵌入和提取过程非常简单,嵌入秘密数据后的图像质量较高。但是,若载体图像的直方图没有较显著的峰值点,则该方法的嵌入容量就非常有限。

图4 基于HS的数据嵌入规则Fig.4 HS-based data embedding rules
3.2.2 基于HS的RDH扩展
Fallahpour等[32]提出基于图像块而不是整个图像的RDH方案。首先,对原始载体图像进行不重叠分块,生成每个分块的直方图。然后,利用各个图像块的零点和峰值点嵌入秘密数据。对每个图像块分别使用嵌入算法可以提高嵌入容量。
Lee等[33]提出利用差值直方图对Ni等[31]的方案进行改进,通过考虑相邻像素间的差值以更好利用自然图像的空间相关性,产生更显著的峰值点。然后,选择在峰值点1和-1嵌入秘密数据。由于最多一半的图像像素被修改,所以嵌入秘密数据后的图像质量不小于51.14 dB。该方案的数据嵌入和提取步骤如下。
步骤1根据M×N大小的原始载体图像I,生成M×(N/2)大小的差值图像D,该过程表示为
D(i,j)=I(i,2j+1)-I(i,2j)
(10)
式(10)中:0≤i≤M-1,0≤j≤(N/2)-1。
步骤2根据差值图像生成差值直方图。同时,将差值为-2和2的差值对进行移位以创建空位用于秘密数据的嵌入,该过程表示为

(11)
步骤3数据嵌入规则定义为
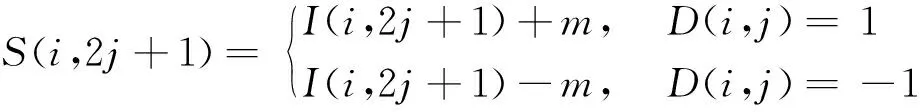
(12)
式(12)中:m∈{0,1}为待嵌入的秘密数据。
步骤4提取过程是嵌入过程的逆过程。先根据M×N大小的嵌入秘密数据后的图像S,生成M×(N/2)大小的差值图像DS,该过程表示为
DS(i,j)=S(i,2j+1)-S(i,2j)
(13)
式(13)中:0≤i≤M-1,0≤j≤(N/2)-1。
步骤5提取嵌入的秘密数据m可表示为
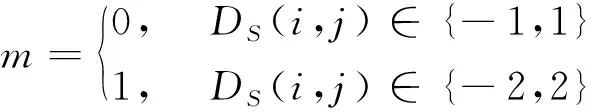
(14)
步骤6恢复原始像素值可表示为
(15)
与原始的基于HS的方案相比,虽然该方案的嵌入性能得到了提高,但是嵌入容量和嵌入秘密数据后的图像质量仍有进一步提升的空间。后来,文献[34]提出基于二维差值直方图修正的RDH方案。该方案通过构造差值对映射来修改二维差值直方图以嵌入秘密数据。在该方案中,每个差值对允许有四个修改方向,更多的像素对可用于嵌入秘密数据,移位的像素对数量也有所减少,从而性能得到了提升。除上述改进策略外,许多基于直方图的改进策略也相继被提出,如多重直方图修正[35]和减少直方图平移中无效像素移位[36]等。与之前的方案相比,这些方案可以提供更好的性能。
3.3 基于PEE的RDH算法
基于预测误差扩展的RDH方案最早由Thodi等[26]于2007年提出。该方案首先生成预测误差直方图(prediction-error histogram,PEH),然后在PEH中嵌入秘密数据。在传统的DE中,像素对的差值用于扩展嵌入秘密数据,最大的嵌入率(BPP)为0.5。在PEE中,预测误差(像素值与其预测值之间的差值)用于扩展嵌入,可将一比特的秘密数据嵌入到一个像素中,最大的BPP可为1。与仅考虑两个相邻像素间相关性的DE不同,PEE利用了较大邻域的局部相关性。由于预测误差值的分布比图像像素值的分布更紧凑,PEH分布更加尖锐,失真就越小。因此,与基于DE和HS的方案相比,PEE具有更优越的性能。
3.3.1 基于一维PEH的RDH方案
基于PEE的RDH方案主要包含PEH生成和对PEH修改两个基本步骤,如图5所示。
常用的像素值预测方法主要有梯度调整预测(gradient adjusted prediction,GAP)[34]、中值边缘预测(median edge detection,MED)[35]、菱形预测[36]等。总体上来看,GAP预测方法具有更好的性能。

图5 PEE嵌入过程Fig.5 The embedding process of PEE
一维PEH的秘密数据嵌入规则如图6所示,扩展和移位规则定义为

(16)

在秘密数据提取阶段,恢复原始预测误差ei可表示为

(17)

与先前的RDH方案相比,该方案具有更好的性能。应该说,该方案的性能依赖于像素值预测的准确性。预测值越精确,生成的直方图就越尖锐,嵌入方案的性能就越好,反之亦然。后来,基于一维PEH的RDH方案得到了广泛的研究和改进。典型的改进策略包含采用自适应的PEH[28,39-41]等。实验结果表明,与先前的方案相比,这些改进方案都具有更好的性能。

图6 一维PEH的秘密数据嵌入规则[42]Fig.6 1-D PEH secret data embedding rules[42]
3.3.2 基于二维PEH的RDH方案
基于一维PEH的方案没有充分利用预测误差间的相关性,预测误差在数据嵌入过程中被单独修改,图像冗余未得到充分利用。事实上,相邻的预测误差间往往是高度相关的。因此,有研究人员提出了基于二维PEH的RDH方案。该方案首先将每两个相邻的预测误差视为一对,生成一个由预测误差对组成的序列,然后通过扩展和移位二维PEH实现数据嵌入。当T=1时,二维PEH的秘密数据嵌入规则如图7(a)所示[注:T=1时,图6(a)中的映射等同于图7(a)中的映射]。限于篇幅,这里只给出第一象限的映射规则,其他三个象限的映射规则与第一象限的映射规则基本相同。
通过深入分析图7(a),发现该嵌入规则有一个缺点,即将(0,0)映射到(1,1)所带来的失真最大,值为2。因此,文献[42]提出丢弃具有较高失真的方向[如第一象限中的(0,0)映射到(1,1)]以尽可能在失真较小的方向上嵌入秘密数据,改进后的映射规则如图7(b)所示。改进后,对(0,0)可嵌入log23位秘密数据,图7(a)中用于移位的对(1,1)可用于嵌入1位秘密数据。因此,与图7(a)相比,使用图7(b)的嵌入规则可以产生更好的性能。然而,如图7(b)所示的秘密数据嵌入规则仅采用了固定的修改方式,所以性能可能不是最佳的。在给定嵌入容量的条件下,为尽可能提升图像质量,文献[44]提出使用自适应的二维映射来自适应地确定二维直方图的修改方式,算法性能得到了提升。总体上来说,基于二维PEH的RDH方案的性能优于基于一维PEH的RDH方案。目前,该方向是RDH的研究热点,众多研究人员正在研究基于多直方图的RDH方案。

图7 二维PEH的秘密数据嵌入规则[42]Fig.7 2-D PEH secret data embedding rules[42]
3.4 基于PVO的RDH算法
像素值排序是从PEE发展而来的一种RDH技术,最早由Li等[45]于2013年提出,其主要思想是首先将载体图像划分为互不重叠的分块,对每个分块中的像素值进行升序排序,然后在最大值和最小值间分别采用PEE嵌入秘密数据。在数据嵌入完成后,每个分块中的像素值顺序保持不变,确保了算法的可逆性。实验结果表明,在低嵌入容量,基于PVO的RDH方案的性能要优于一些基于PEE的方案。但是,对纹理丰富的图像来说,基于PEE的方案优于基于PVO的方案。
在文献[45]中,通过将PVO与PEE相结合,可以减少移位像素的数量,从而提升图像质量。对于每个分块,用分块中的第二大像素值来预测最大像素值,用第二小像素值来预测最小像素值。然后,预测误差1和-1分别用于扩展嵌入数据。以预测最大像素值为例,基本的数据嵌入和提取步骤如下。
步骤1将载体图像划分为互不重叠的大小相同的分块。对于包含n个像素的分块X,升序排序其像素值(x1,x2,…,xn),得到(xσ(1),xσ(2),…,xσ(n))。其中,σ:{1,2,…,n}→{1,2,…,n}是单射,若xσ(i)=xσ(j)且i 步骤2用该分块中的第二大像素值xσ(n-1)来预测最大像素值xσ(n),相应的预测误差为 emax=xσ(n)-xσ(n-1) (18) 步骤3预测误差的扩展和移位规则可表示为 (19) 式(19)中:m∈{0,1}为待嵌入的秘密数据。 步骤4嵌入秘密数据后的像素值可表示为 (20) 步骤5提取过程是嵌入过程的逆过程。将嵌入秘密数据后的图像划分为互不重叠的大小相同的分块,对于包含n个像素的分块Y,升序排序其像素值(y1,y2,…,yn),得到(yσ(1),yσ(2),…,yσ(n))。 步骤6得到排好序的像素值(yσ(1),yσ(2),…,yσ(n))后,相应的预测误差为 (21) (22) 步骤8恢复原始像素值可表示为 (23) 实验结果表明,该方案在低嵌入率时具有更高的PSNR。然而,该方案仅在一个方向上进行预测误差扩展以嵌入秘密数据,嵌入容量有限。后来,文献[46]对该方案进行了改进。以预测最大像素值为例,通过考虑最大像素值和第二大像素值的像素位置[式(24)],可以将秘密数据嵌入到最大像素值等于第二大像素值的分块中以充分利用平滑块。然后,预测误差1和0用于扩展嵌入秘密数据[式(25)],提升了嵌入容量。 (24) (25) 但是,深入研究该方案后发现该方案对每个分块中最大和最小预测误差的修改是独立进行的,导致性能并不一定是最佳的。文献[44]通过将每个分块中的最大和最小预测误差视为一对,基于平滑图像块的预测误差对生成二维直方图,然后自适应地修改生成的直方图来实现秘密数据嵌入,很好地利用了预测误差间的相关性,优化了嵌入性能。后来,Ou等[47]提出了对于每个分块,最大的两个像素和最小的两个像素被分别分组为两对,然后使用第三大像素和第三小像素来预测的PVO方案;Zhang等[48]同时考虑像素值顺序和像素位置,提出基于位置的LPVO(location-based pixel-value-ordering)方案。实验结果表明,与原始方案相比,这些改进方案的性能都得到了提升。对于现有的RDH方案来说,在低嵌入率时,在相同的BPP条件下,基于PVO的RDH方案的PSNR是最好的。因此,若嵌入容量需求不高,嵌入秘密数据后的图像质量要求较高的话,采用基于PVO的方法应该是一种较好的选择。 与传统的RDH算法相比,基于IT的RDH算法具有单层嵌入容量大和视觉质量高等优点,目前已成为RDH技术的研究热点。该类算法的主要思想是利用原始像素值作为参考,通过插值算法来预测新像素值。嵌入秘密数据时,秘密数据仅被嵌入到插值像素中,插值图像中的原始像素值保持不变。在提取阶段,原始图像的恢复非常简单,仅需对嵌入秘密数据后的图像进行下采样即可。 基于IT的RDH算法流程如图8所示。在发送端,一幅N×N大小的输入图像首先被下采样生成(N/2)×(N/2)大小的原始图像,然后对原始图像使用插值算法生成N×N大小的插值图像。在接收端,通过对N×N大小的嵌入秘密数据后的图像进行下采样操作恢复原始图像。需要注意的是,在输入图像上直接进行插值操作也是可行的。现有的算法基本采用基于下采样的方案,其原因主要是可以评估插值算法和嵌入秘密数据后的图像与输入图像的性能。 到目前为止,已经提出了很多有效的图像插值方法,如最近邻插值(nearest neighbor interpolation,NNI)和双线性插值(bilinear interpolation,BI)等。NNI方法通过选择原始图像中最近邻点的像素值来生成相应的插值像素,但是,该方法通常会受到混叠效应的影响。BI方法通过对4个最近的相邻原始像素进行加权计算生成相应的插值像素,与NNI方法相比,该方法生成的图像外观更平滑,视觉质量更好。 图8 基于IT的RDH算法流程图Fig.8 Flow chart of RDH algorithm based on IT 2009年,Jung等[50]提出了邻域均值插值(neighbor mean interpolation,NMI)方法,通过计算相邻像素值的平均值产生插值像素,然后通过计算插值像素与一个原始像素间的差值以在插值像素中嵌入相应位数的秘密数据。该方法的数据嵌入和提取过程如图9所示,详细步骤如下。 步骤1对原始图像使用NMI插值算法,生成插值图像,该过程可表示为 (26) 步骤2插值像素与原始像素I(0,0)间差值的绝对值计算为 (27) 步骤3根据计算出的差值来确定每个插值像素可嵌入的秘密数据长度,该过程表示为 (28) 步骤4取n1、n2和n3位秘密数据并分别转换为十进制V1、V2和V3。 步骤5嵌入秘密数据后的像素值为 (29) 步骤6在提取阶段,仅通过嵌入秘密数据后的图像就可以提取秘密数据并恢复原始图像。提取的秘密数据的十进制可表示为 (30) 图9 基于IT的RDH算法嵌入过程Fig.9 The embedded process of RDH algorithm based on IT 步骤7将提取的数据V1、V2和V3分别转换为n1、n2和n3位二进制数据,即可得到嵌入的秘密数据。 大量的实验结果表明该方法提供的最大嵌入率(BPP)可达到1.76,比NNI和BI方法更有效。根据式(28),可以得到嵌入的秘密数据量会随差值的增大而增大。然而,该方法在计算差值时仅局限在一个2×2的分块中,限制了嵌入容量。 后来,Lee等[51]提出了基于邻域像素插值(interpolation by neighboring pixels,INP)的RDH方法。在该方法中,首先计算每个3×3重叠分块中4个原始像素的最大值,然后通过计算每个插值像素与最大值间的差值来确定可嵌入的秘密数据量。实验结果表明该方法的BPP可达到2.27,能够产生比NNI、BI和NMI更高的PSNR,表达式为 (31) Chang等[52]提出了基于增强邻域均值插值(enhanced neighbor mean interpolation,ENMI)的RDH方法,通过采用4个最接近的原始像素的平均值替代NMI中对角插值像素的计算,提升了图像质量,表达式为 (32) Malik等[53]提出了改进的邻域均值插值(modified neighbor mean interpolation,MNMI)方法。相较于NMI方法,该方法在计算水平插值像素时,其左右相邻像素被赋予更多权重,在计算垂直插值像素时,其上下相邻像素被赋予更多权重,表达式为 (33) 就视觉质量效果而言,与在计算对角插值像素时利用水平和垂直插值像素的NMI和INP方法相比,ENMI和MNMI方法能够获得更高的图像质量。 总体上来看,与传统的RDH技术相比,基于IT的RDH技术因可以在每个插值像素中嵌入多比特的秘密数据,所以嵌入率可达到2.0以上,真正地实现了大容量的秘密数据嵌入。在实际应用中,若需在载体图像中嵌入大容量的秘密数据,采用基于IT的方案可以说是一种较理想的选择。 可逆数据隐藏技术是当前的热点研究领域,其主要思想是通过可逆变换对载体信号进行处理以嵌入秘密数据。在数据提取和载体信号恢复阶段,不仅能将嵌入的秘密数据完全提取出来,而且还能实现对原始载体信号的无损恢复。基于空间域的可逆数据隐藏技术通过对载体信号进行直接修改来实现秘密数据的嵌入,可以很好地避免在载体信号变换过程中可能出现的少量数据丢失的情况,实现对原始载体信号的完整恢复。 首先对可逆数据隐藏技术的基本框架和性能评估进行简要分析。其次,对基于差值扩展、直方图平移、预测误差扩展、像素值排序和插值技术等五种典型的可逆数据隐藏技术分别进行了介绍和讨论,给出了每种典型技术的嵌入和提取过程,以更好地帮助读者加快、加深对基于空间域图像的可逆数据隐藏的了解。 对于可逆数据隐藏技术来说,嵌入容量和嵌入秘密数据后的图像质量是两个最重要的性能指标,现有的方案都旨在提升它们的大小。然而,嵌入容量和嵌入秘密数据后的图像质量是一对矛盾体,嵌入容量越高,嵌入秘密数据后的图像质量往往越低,反之亦然。因此,新设计的RDH方案都旨在一定的嵌入容量条件下,尽可能地提高嵌入秘密数据后的图像质量,这也是目前RDH技术的重点和难点。为进一步提升RDH方案的性能和实用性,RDH技术可从以下几个方面去开展。 (1)提升压缩数据的性能。在RDH技术中往往需要采用压缩技术对相关数据进行压缩以增加冗余空间嵌入更高容量的数据。例如,对于基于DE的RDH技术来说,需对嵌入过程中产生的辅助信息进行压缩以减少其占用嵌入空间的比例。然而,现有的数据压缩性能都有限。为提高压缩率,可能需要根据待压缩数据自身的特征使用不同的压缩方式才能产生更好的性能。 (2)对彩色图像RDH技术进行研究。到目前为止,针对灰度图像的RDH技术已非常成熟,而针对彩色图像的RDH技术较少。同时,若直接将灰度图像RDH技术移植到彩色图像中,性能一般不会很好。此外,在实际应用中,彩色图像比灰度图像更受欢迎。因此,对彩色图像RDH技术开展研究更具有实际意义。 (3)对压缩域图像开展研究。当前,大多数RDH技术主要针对的是未压缩图像。然而,在日常生活中,为节约存储空间和传输带宽,压缩后的图像更实用。因此,设计基于压缩域的RDH技术可能更具有现实意义。目前,虽然已有基于JPEG压缩域的RDH算法,但是性能还有待进一步提高。 (4)与人工智能合作。深度学习技术已在多个领域被成功应用。因此,研究人员在设计RDH算法时可以尝试将深度学习技术引入到RDH中来以进一步提升嵌入算法的性能。目前,已提出一些基于深度学习的RDH算法,如文献[61]。相信随着深度学习技术性能的不断提高,结合深度学习技术来设计新型的RDH算法将成为未来的研究热点。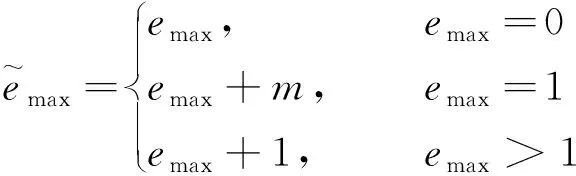
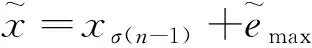




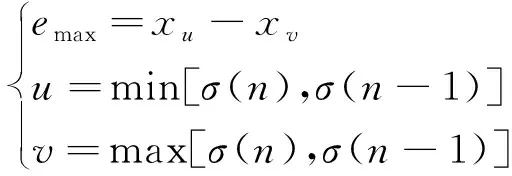
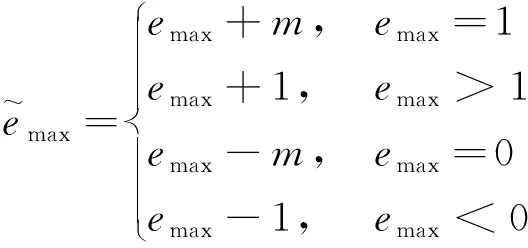
3.5 基于IT的RDH算法







4 结论和展望
