借助中点精准溯源，探究一题多解本质

鲍利辉

（杭州师范大学东城中学 浙江杭州 310019）

作为从初中几何学习初便涉及的知识点，“中点”有诸多相关知识点与衍生知识点，内容体系相对复杂，因此学生在面对题目中此类条件时会显得手足无措，无从入手.只有在整体视角下对这些知识点进行梳理，结合具体的图像，实现精准溯源，才能真正理解与掌握中点相关的知识网络，从而达到一题多解。

一、知识溯源分析法的意义

在平常教学过程中，经常存在解法单一的情况，究其根源与忽视对多解生成本源的思考有关。就数学转化思想而言，所有的数学问题都可以用已经学过的知识解决，但究竟如何联系却是教学过程中的难点。教师在教学过程中经常教的是“怎么做”，因此学生在实际解题过程中往往存在思维定势.为了突破这一困局，教学应当以“怎么想到这么做”为切入点，建构起“条件—知识源”之间的关联，并以此为抓手加强学法指导，切实提升学生分析问题和解决问题的转化能力[1]。

知识溯源分析法关键有三步：明确解题目标；追溯知识源；选择知识源。知识溯源分析法的优势性在于：通过目标锁定明确解决问题的思考方向，借助知识溯源掌握处理问题的转化策略，依据过程分析提升受阻思维的调控技巧，从而不仅详细地剖析辅助线生成的来龙去脉，在呈现“怎么做”的同时更加明晰“为什么这么做”，强化对学生转化能力和迁移能力的有效培养[2]。

二、基于图形载体的中点溯源

借助知识溯源分析法，可以在初中数学中，对中点有关的知识点在整体视角下基于图形的载体进行精准溯源。首先在初中里面和中点直接有关的第一个概念便是中线。在初中的学习过程中，可以把三角形的种类作为分类依据，对中线作用进行梳理。在任意三角形中的中线作用为平分线段，平分面积。而在等腰三角形中，中线的另一作用便是三线合一，即底边上的中线、高线和顶角的角平分线重合。在直角三角形中，斜边上的中线又衍生出来斜中线定理[3]。

另外一个中点衍生知识点便是中位线。与中线不同的是，连接同一个三角形两边上中点时，便产生了中位线。当然，中位线的难点不仅仅是找到中位线，而更重要的是能在解题过程中理解中位线平行于第三边且等于第三边的一半，因此这里要建立二级链接，即中点-中位线-三角形第三边。

其次，如果中点和垂线相联系，便会产生中垂线，中垂线的性质非常丰富，其最重要的性质为中垂线上的点到线段两端距离相等。而同一个三角形中三边上的中垂线相交，便构成了三角形的外心，三角形的外心又是圆中的一个重要概念。

最后，将中点放在圆中来看，除了弦的中点还可以是弧的中点，而不论是哪种，都可以与垂径定理建立联系，而将弧的中点和弦的中点作为能相互推导的结论，便可以联想到圆心角定理及其推论，而弧与圆周角度数是一一对应的，因此也可以联想到圆周角定理。

三、借知识溯源探本质

实际上能够根据条件联想到所需要的知识源固然重要，但只根据知识源也不能做到一题多解，解法多样，最重要的不仅仅是关注多解的挖掘，更重要的是关注对多解生成本源的思考。下面在知识溯源的基础上，以具体题目为例探究一题多解生成的本质。

1.基于选择知识源不同产生多解

例1.如图，已知H是△ABC的垂心，O是外心，OL⊥BC于L.求证：AH＝2OL。

分析：对于这道题目而言，条件较为简单。其中垂心的作用，便是延长构造出诸多的垂线。而三角形的外心很自然地可以联想到构造△ABC的外接圆，因此可以得到第一种方法。

另外基于外心，可以逆向追溯，从外心的本质入手，中垂线与垂心相互联系，可以得到多对平行，再结合中位线的性质，可以构造出来平行四边形，因此得到第二种方法。

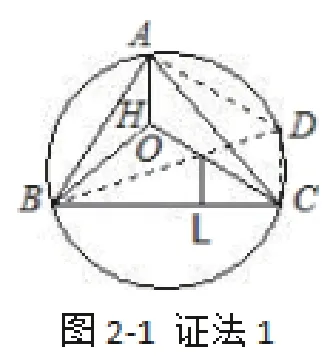
证法1：如图2-1，作△ABC的外接圆⊙O，连接BO并延长交⊙O于D，连接CD，AD，由中位线易得CD=2OL.又因CD⊥BC，AH⊥BC，可得AH∥CD.同理，AD∥HC，得四边形AHCD为平行四边形，可得AH=CD，即AH=2OL。

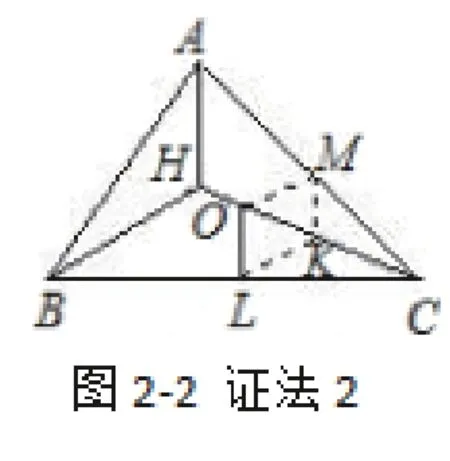
证法2：如图2-2，作OM⊥AC于M，取CH的中点K，连接MK，LK，则有MK∥AH∥OL，LK∥BH∥OM，可得四边形OLKM为平行四边形，则MK=OL.又MK＝AH，所以AH=2OL。

证法比较：两种方法基于不同的处理路径，一种是基于外心的合情推理，一种从外心的本质出发，再由中点进一步联想，通过中位线进行联系，两种方法殊途同归，不分伯仲，也切实证明了选择知识源不同多解可行性。

2.基于构图位置不同产生多解

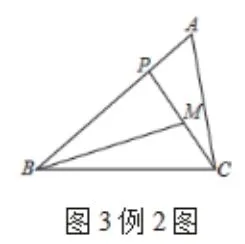
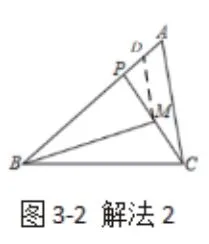
例2：在△ABC中，P为边AB上一点.M为CP的中点，AC＝2，AB＝3，∠PBM＝∠ACP，求BP的长。

分析：基于题目中所给的∠PBM＝∠ACP，可以延长BM与AC相交，这样便可以得到两对相似，进而由两对相似的对应线段比构造等量关系可以求出BP的长。

从另一个角度来看，当一个中点无法形成有效联想，那么从题中观察到，如果取AP的中点可以构造出中位线，而这条中位线既可以联系AC，又可以将转换到∠PBM和∠ACP斜A型相似的基础模型中，从而构造方程求解。其次，如果把BM当作中位线考虑，可以通过倍长BP的方式构造出相似三角形，同样也可以求解。

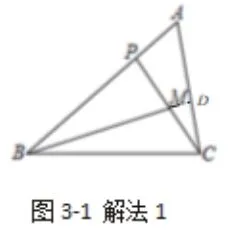
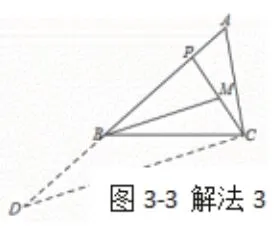
解 法3：如 图3-3，延 长PB至 点D，使BP=BD，连接CD.设BP=x，则PD=2x，∠PBM=∠ACP=∠PDC，∠PAC=∠CAD，可得△APC～△ACD.由AC2=AP·AQ得22=（3-x）（3+x），可得BP=x=

解法比较：对于上述三种解法，可以看到，如果单单把中点当作中线来考虑，虽然也可以解决该问题，但是不管从计算量还是思维难度上来讲都要求较高。但如果将中点放在中位线的角度来看，通过合理地添加辅助线，可以有效减少计算量，减少思维的难度，并且将图像转换到我们熟知的A字形和斜A型相似，利用射影定理能快速求解。

3.基于辅助线的表述不同产生多解

同一辅助线从不同的角度描述，往往会产生不同的解题思路。以例题2解法3为例，较为简单的，若辅助线的表述为“延长PB至点D，使PD=2BP”，那么需要从PD=2BP推得BM为中位线。若辅助线的表述为“作CD//BM，交AB延长线于D”，需要通过CD//BM推得△BPM～△DPC，进而得到BP=BD。再进一步，辅助线的表述还可为“作∠BCD=∠CBM，交AB延长线于D”，此时需要从∠BCD=∠CBM得到BM//CD。

解法虽然并不会因为辅助线的作法不同而产生思路上本质的改变，但是不同辅助线的表述及后续的推导过程也体现了数学的严谨性与逻辑性，而这恰恰也是学生经常忽略并所欠缺的点。

4.基于不同知识体系的关联性产生多解

例3：如图，AB是⊙O的直径，且AB＝10，弦CD⊥AB于点E，G是弧AC上任意一点，延长AG，与DC的延长线交于点F，连接AC，BC，DG.若求DG的长。

分析：题目中的弦CD⊥AB，AG=BG很自然联想到垂径定理，由垂径定理可以得到AB⊥OG，那么很自然地联想到求DG的长度便是构造直角三角形，利用AB＝10很容易得到所需的直角三角形的各边长，从而求解。从不同知识体系上讲，建立平面直角坐标系求点D、G的坐标，从而通过两点间距离公式求出DG的长度。

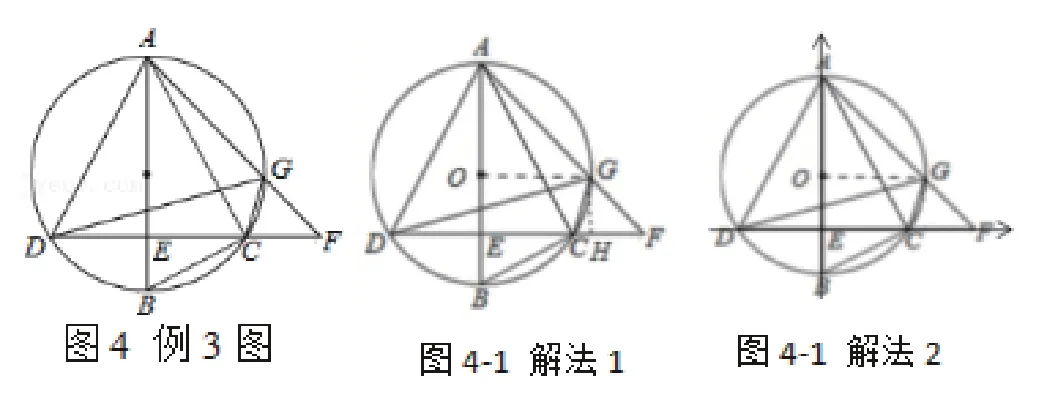
解法比较：两种解法虽然在解题过程中有所相似，但垂径定理在两个种解法中起到的作用却有所差异。但两种解法起始的知识体系有着本质的不同，第一种解法是立足于几何的图形直观，通过寻找线段的等量关系，再结合求不共线线段的长度一般性做法求解。另一种是基于解析几何的一般观念，通过求点的坐标，再结合已经有的公式进行求解。这种多解的思考过程，无疑拓宽了思维的广度。

四、教学导向

1.构建知识网络，提高知识完备性

初中阶段学生对需要作辅助线的题目感觉到困难的原因，很大一部分是教师很多时候只教怎么做，不教怎么想，教师只分析解题过程，学生的“懂”，也仅仅停留在解题过程中的听懂层面，并未了解解题思路生成的本质。因此教师在教学过程中更加应当关注基于条件的知识溯源挖掘，帮助学生构建更加严密完整的知识网络，并能够打通各块知识之间的联系，而这又离不开教师本身对于教材知识的发掘与整理，只有教师做到知识体系的充分完整，才能够让学生体会到各部分知识之间的联系。当学生的知识网络逐渐完善，那么辅助线的作法自然不在话下，一题多解便能有其生长的基础条件。

2.掌握基本构图，提高转化能力

然而事实上很多时候就算有完备的知识储备，解题过程也并非一帆风顺，遇到困难也在所难免。这就要求教师在日常教学过程中更应该对一些重要的转化技巧进行提炼、总结、升华。首先学生应掌握基本图形的构图策略，这是提升学生转换技巧的重要途径，例如倍长中线和构造中位线是处理线段中点的两大基本技巧，构造A字形、八字形相似也是建立边与边之间联系的重要桥梁。其次，重现图形的演变过程更有利于理解，例如先将复杂图形的基本结构抽离出来，让学生进行辨识，紧接着逐步添加线段或图形演变为最终图像，让学生一步步分析，明确添加的线段的作用以及将会产生的关联，帮助学生系统性地学习分析问题的方法，这样一题多解才有生长点。