泰勒公式的应用研究

孙研博 钱 莹 李东

（佳木斯大学 黑龙江佳木斯 154007）

泰勒公式作为连接分析学及代数学行列式部分理论的有力工具，在极限的计算、近似估计、线性插值等方面有着重要应用。事实上，泰勒公式虽然结构复杂，但其却存在较强的规律性，不仅方便记忆，甚至在解决部分问题时能使原本困难的过程化繁为简，起到事半功倍的效果，是理解和处理复杂数学问题的有力途径[1]。此外，在经济学、统计学、金融学等领域出现的部分实际问题也同样可以用泰勒公式来解决。所以关于泰勒公式的相关运用已经不局限于数学层面。

泰勒公式好比是一元函数微分学的奠基石，一元微分学中相当多的问题都可以归结为泰勒公式求解，它是一种用函数及其n阶导函数在某一定点的值来表示其附近一系列值的公式，将复杂的函数简化为多项式函数[2]。在高等数学解题中，泰勒公式具有一定的优越性，它是简单而有效的工具。针对泰勒公式这种可以化繁为简的功能，本文将以泰勒公式在极限计算，近似计算，线性插值及在行列式中的应用的应用展开讨论。

泰勒定理：

设函数f(x)在区间(a,b)上n+1阶可导，且导函数连续，那么取x0(a,b)

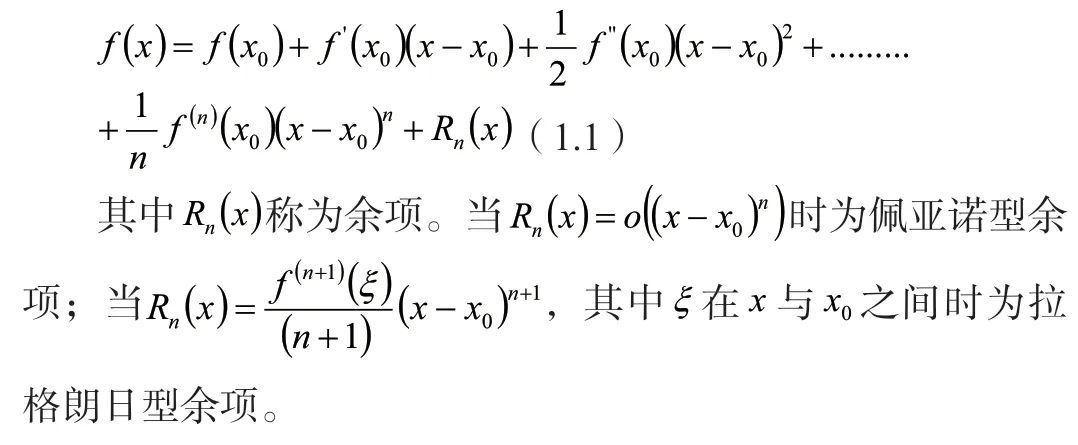
注：当x0=0时，将其代入（1.1）所得结果被称为麦克劳林公式。

一、泰勒公式的应用

1.利用泰勒公式简化极限计算

极限贯穿于高等数学的始终，我们常见的解决极限的方法有：定义法、迫敛性准则、洛必达法则、分母分子有理化等。洛必达法则通常用于解决0比0型或无穷比无穷型此类未定式的极限，而对于那种对分子分母分别求导麻烦式子应用起来就较为不便。对于需要多次求导的式子求极限我们可应用泰勒公式进行简化计算。

因此可知，对分子应用泰勒展式，若展开项最高次幂小于3，虽然在形式上简化了计算，但是最终原式依然化为型不定式，不能进行求解。

从而我们可知，对分子应用泰勒公式时，若展开项次幂最高大于3，最终得到正确结果。但是如果次幂越高，那么将其展开的话较为烦琐，计算容易出现失误。

我们看到，当展式的幂次最高大于3和等于3时，最后计算的分子都含有高于分母幂次的无穷小阶数，然而该项的计算结果仍然为0.这是由于泰勒公式的本质是将某一个函数转化为一个多项式函数，而且随着展开项数的增加，其中无穷小的阶数也在增加。所以我们根据高阶无穷小的递推可知：若某一个函数的泰勒展开式满足x的n阶无穷小，那么它必定满足x的小于n阶无穷小。

2.利用泰勒公式求近似值

例3：利用泰勒多项式逼近函数sinx，并要求其中的误差≤ 1 0-3。试分别在m=1和m=2两种情况下计算：x的取值范围。

当m=1 时，sinx≈x，使其误差满足

如果利用泰勒公式展开更高次幂来逼近sinx，x能在更大范围内满足同一误差。

3.泰勒公式在线性插值中的应用

当n=1 时就是梯形公式了。

例4：证明梯形公式

假设：

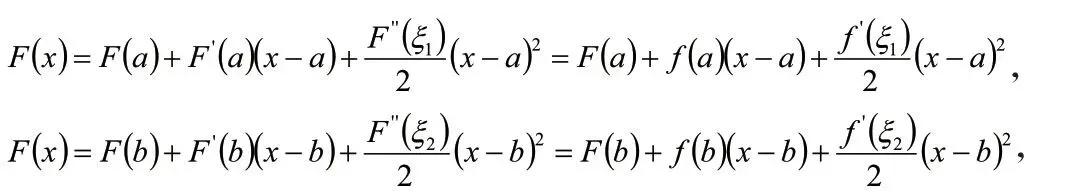
将x=b带入第一个式子，得到

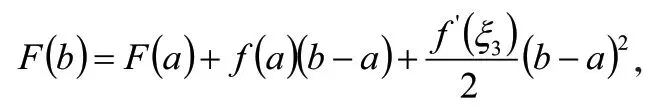
将x=a带入第二个式子，得到

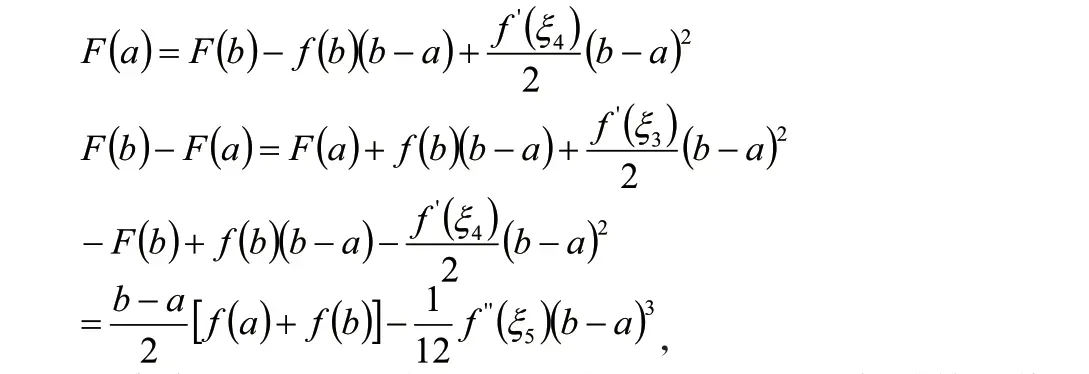
结合泰勒定理和牛顿-莱布尼茨公式，得出近似计算数值积分的梯形公式

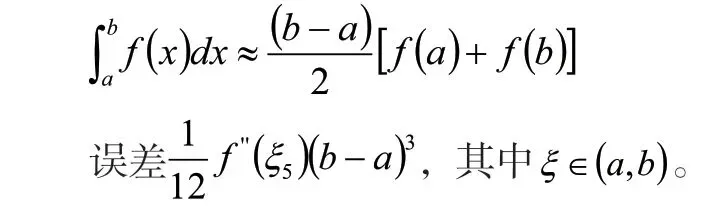
4.泰勒公式在行列式中的应用

在计算行列式时，多数情况下我们采用展开式或者其他纯代数型的方法进行计算，比如数学归纳法、代数知识传递法方法，知识原理（例如微积分）很少用于计算行列式。我们从此特性中发现泰勒公式更适合计算行列式。我们首先可以了解需要的行列式的特征，观察其形式并研究其性质，然后为其构造行列式的适当的函数，再根据泰勒公式在某个点上扩展行列式的功能，最后找到行列式。

例5：求解n阶行列式

分析：如果一个行列式可以将其看作关于x的函数（一般是x的n次多项式），记作f(x)，我们利用泰勒公式将在某点x0展开，这样便可以求解行列式的值。

解：记f(x) =D，利用泰勒公式在点z处展开：

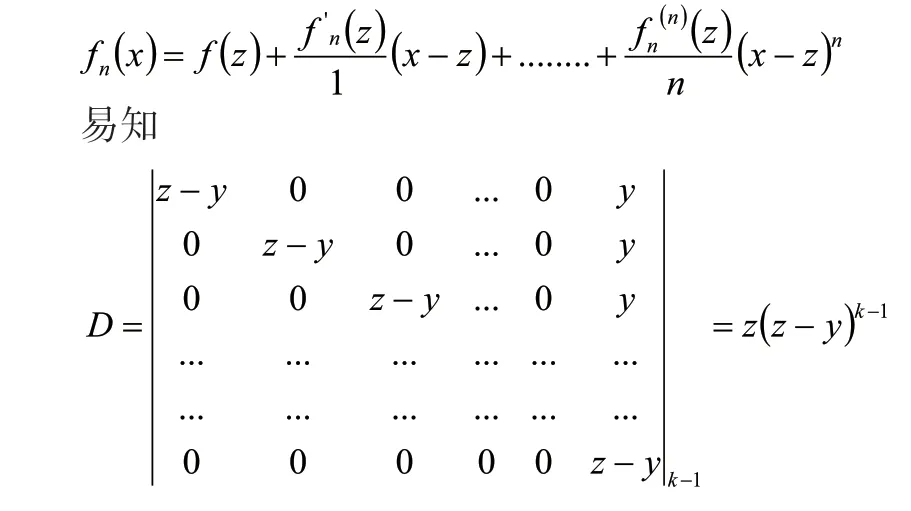
由上式可得，fk(z)=z(z-y)k-1时都成立。

根据行列式求导的规则，

于是在x=z处的各阶导数代入得到

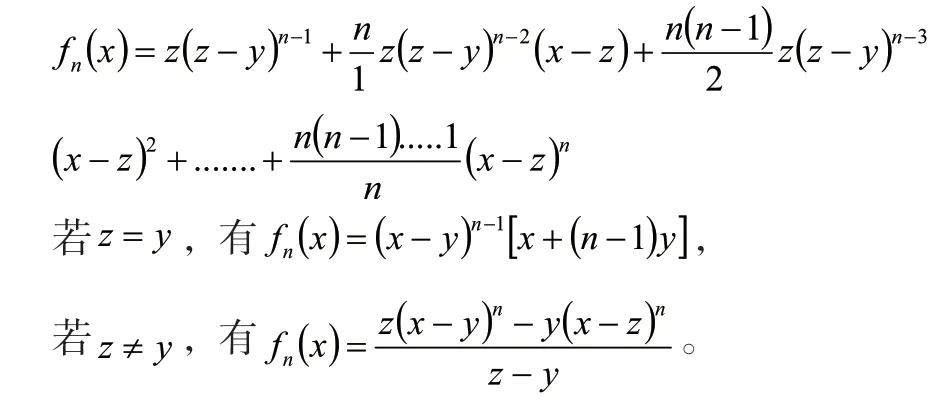
5.利用泰勒公式判断敛散性

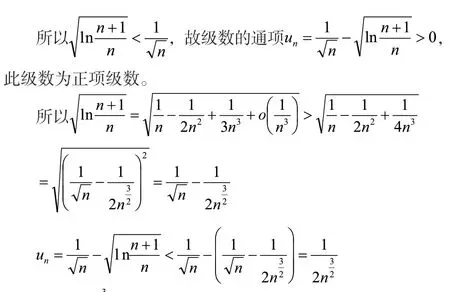
当题中所给的级数通项表达式是很多各式各样类型的函数式组合而成的，则很难直接看出来的复杂形式，并且用我们常用的方法不知从何下手的时候，这时就可以考虑尝试运用泰勒公式，把题目中所给的级数通项变换成统一的形式，然后再进行敛散性的判定。

结语

本文从主要从四个方面探究了泰勒公式在分析和研究数学问题等方面的应用，用一些例子说明其应用方法，补充了高数教材中相关内容，有助于加强学习者对泰勒公式的理解和掌握及应用方法，对更深入的理解和掌握抽象定义起到一定作用。

作为理解和深入发掘函数极限的重要理论根据，泰勒公式是高数教材中的重要研究课题，它可将一些难以研究的函数近似地转化成为更方便思考的多项式函数。同时泰勒公式作为深入探索函数深层次问题的重要媒介，其在导数及微分的问题、根的存在性问题、相关不等式证明中也有着广泛的应用；泰勒公式是数学分析问题的一个重要媒介，多数常见的方法解决比较烦琐时，尝试运用泰勒公式可能会豁然开朗，通过实例发现泰勒公式在微积分学中理论支撑及复杂计算中的运用，感受运用泰勒公式的便捷性；泰勒公式简化了复杂的问题，实现了精确度和精确度，并且可以应用于除了数学外的多个其他学科。泰勒公式在数学下设的许多分支领域中都有过具体的应用实例，但是仍有部分学派不同意或者说很少地发表关于泰勒公式的谈论。这是因为他们认为泰勒公式及泰勒定理所给内容和理论支撑不够严密，不能完美地适用于解决问题。由此可见，有关泰勒公式的应用仍有完善和提升的空间，值得我们深入地挖掘其中的奥妙。