立体几何中有关交线问题的解决方式
2022-09-29舒铖蓓
舒铖蓓
(浙江金华第八中学 浙江金华 321000)
空间问题平面化是解决立体几何问题的一种重要的思想方法,而截面是重要的载体,所以立体几何中寻找和构造截面是常见的问题,实则是画出截面与几何体的表平面的交线。对于此种问题,本文给出两种解决方式。
一、理论依据
解决立体几何问题,主要用几何法和代数法。
用几何法解决平面与平面的交线问题,要用到以下几个定理:
1.基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
2.线面平行的性质定理:一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行。
3.面面平行的性质定理:两个平面平行,如果另一个平面与这两个平面相交,那么这两条交线平行。
4.线面垂直的性质定理:一条直线与一个平面垂直,那么这条直线与平面内的任意一条直线垂直。
用代数法解决平面与平面的交线问题需要用到以下知识:
2.空间中两平面交线的一般方程:已知Π1,Π2是空间中的两个相交平面,Π1:A1x+B1y+C1z+D1=0,Π2:A2x+B2y+C2z+D2=0,则两平面交线的一般方程为
二、实例展示
【例1】如图1所示,在正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,求证:MN//AA1B1B。
【解析】要证MN//AA1B1B,只要在平面AA1B1B内找到一条直线与MN平行,难点在于:一方面在平面AA1B1B内没有明显的直线与MN平行,需作辅助线;另一方面利用条件CM=DN证明平面AA1B1B内的辅助线与MN平行。
【思路1】第一步,借助分析法,若MN//AA1B1B,则过MN构造平面与平面AA1B1B相交,所得交线与MN平行,这也是在平面AA1B1B内作出与MN平行的辅助线的方法。
第二步,如图2所示,过点N作NP//AD,过点M作MQ//BC,因为AD//BC,所以NP//MQ,NP与MQ唯一确定平面MNPQ。连接P、Q,所以平面MNPQ与平面AA1B1B的交线为PQ。
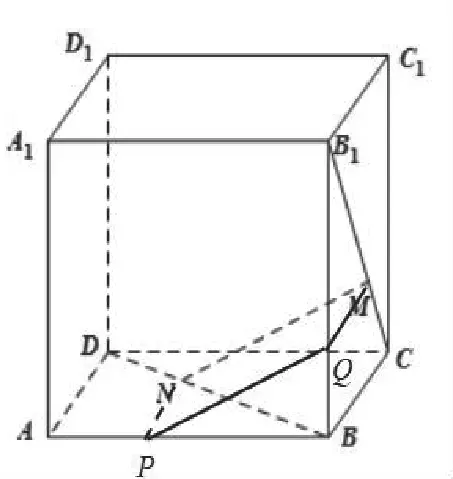
图2
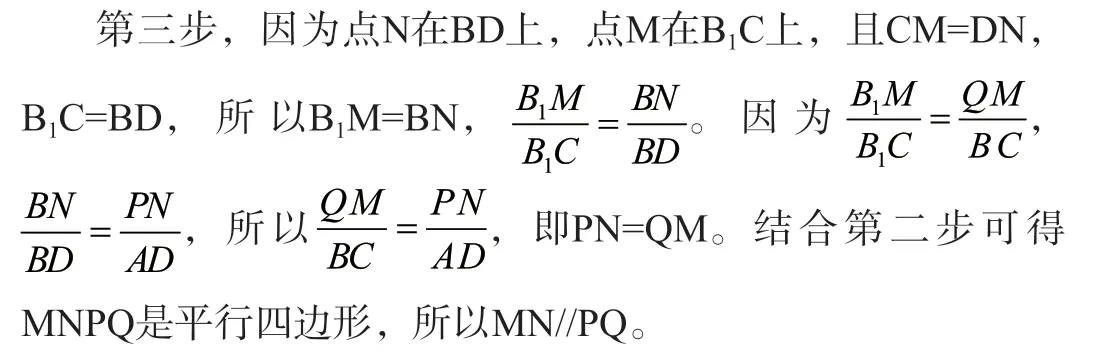
第四步,由MN//PQ证出MN//AA1B1B。
【思路2】第一步同思路1。
第二步,如图3所示,MN与B1C相交于点M可唯一确定平面CMN。延长CM至CB1,连接C、N,延长CN交BA的延长线于点H,所以平面CMN延展至平面CB1H。连接B1、H,所以平面CMN与平面AA1B1B的交线为B1H。
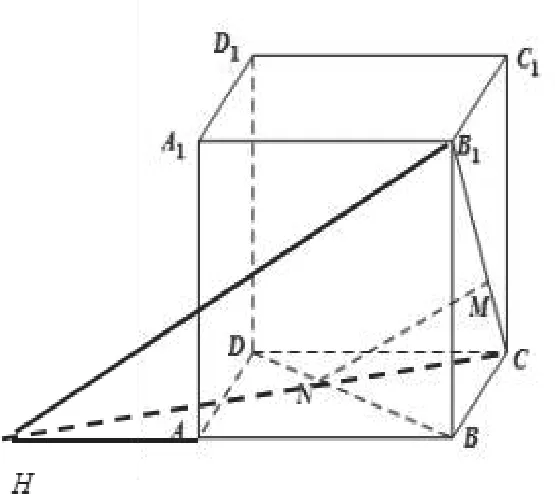
图3

第四步,同思路1。
点评:思路1利用两条平行线构造平面,思路2利用两条交线构造平面。两种思路都用到基本事实3画出交线,思路2需要延展平面再画出交线。
【例2】(2018课标1卷理12)已知正方体的棱长为1,每条棱所在直线与平面α所成角都相等,则α截此正方体所得截面面积的最大值为( )

【解析】条件“每条棱所在直线与平面α所成角都相等”包括三个几何对象:棱、面、线面角。对这三个对象的处理如下:“每条棱”转化为从同一顶点出发的三条棱,平面α需要寻找和构造,线面角可用几何法或者代数法求得。
【思路1】如图4所示,第一步:每条棱所在直线与平面α所成角相等化归为以D为公共顶点的三条棱DC、DA、DD1所在直线与平面α所成角相等。
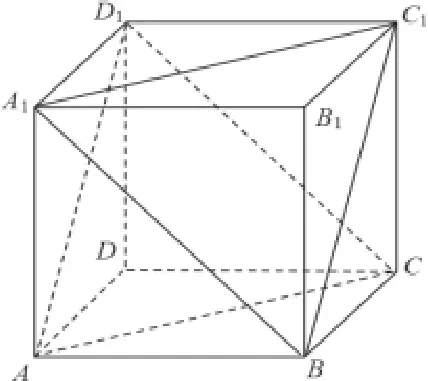
图4
第二步:因为D-ACD1是正三棱锥,所以三条棱DC、DA、DD1所在直线与平面ACD1所成角相等。
第三步:平面α是平面ACD1或者与平面ACD1平行的截面,例如平面A1BC1。下面介绍如何画出与平面ACD1平行的其它截面。
若动态平移平面ACD1,借助直观想象可得如图5和图6两种不同的截面形状。画截面实则画出截面与正方体的表平面的交线,因为截面与平面ACD1平行,又因为两个平行平面与第三个平面相交所得的交线平行,所以图5中在DD1上任取一点M依次画平行线得到截面MNP,图6中在A1D1上任取一点E依次画平行线得到截面EFGHIJ。

图5

图6
因为截面MNP的面积小于截面ACD1的面积,所以要求α截此正方体所得截面面积的最大值,只要分析截面EFGHIJ的面积何时最大。先画出截面EFGHIJ的平面图形(如图7所示),再设A1F=a,可求得截面EFGHIJ的面积为当截面面积的最大值为
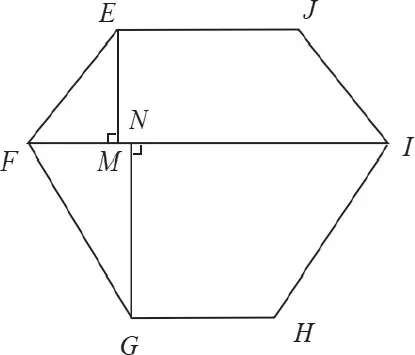
图7
【思路2】第一步,与思路1相同。
第二步,用向量的坐标代数法求线面角。

代入用向量坐标表示的线面角公式可得
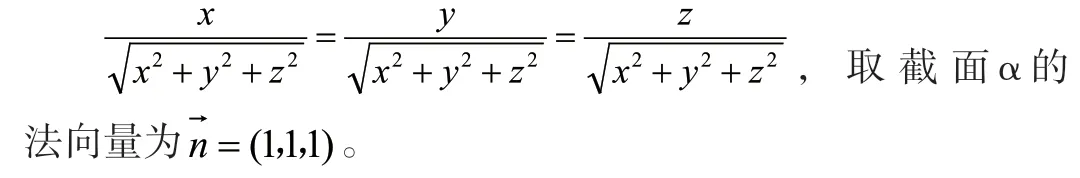
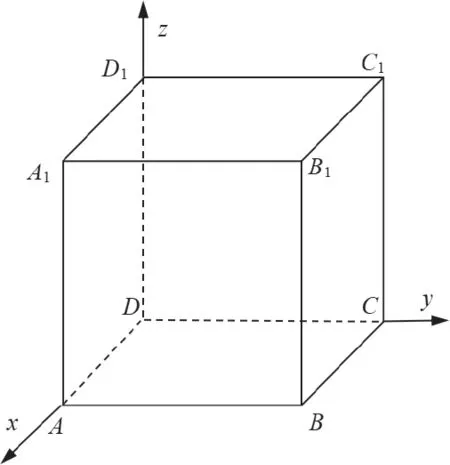
图8
第三步,用向量的坐标法寻找截面α。由截面α的法向量可知棱DD1所在直线与截面α有交点,例如交点为点D1=(0,0,1),设截面α上任一点M(x,y,z),由求得截面α对应的方程为x+y+z=1。由联立得y+z=1,由数到形,画出截面α与平面yoz的交线CD1。同理求出截面α与正方体的表平面的其它交线从而找到截面ACD1。若棱DD1所在直线与截面α的交点分别取在线段DD1或者线段DD1的延长线上,同第三步中的方法可画出截面α如图5、图6。
【点评】思路1的巧妙之处在于利用正三棱锥模型发现截面α的特殊情形,再用面面平行的性质定理构造出其它截面类型。思路2的难点在于截面α以及截面α与正方体的表平面的交线的坐标表示,学生在高中阶段并不熟悉该种表示,需要先铺垫再介绍该方法。
【例3】在方体ABCD-A1B1C1D1中,E为CC1的中点,P、Q是正方体表面上相异两点,满足BP⊥A1E,BQ⊥A1E。若P、Q均在平面A1B1C1D1内,则PQ与BD的位置关系 。
【解析】我们可以从两方面解读条件“BP⊥A1E,BQ⊥A1E”:一方面空间中两条直线垂直可以是异面垂直,也可以是共面垂直;另一方面满足该条件的点P(点Q)不唯一,该题目难点在于求出满足条件的点P(点Q)的集合,下面介绍两种方法。
【思路1】如图9所示,第一步,借助空间想象,点P(点Q)在过点B且与A1E垂直的平面上。第二步,在正方体中画出过点B且与A1E垂直的截面,实则画出截面与正方体的表平面的交线与A1E垂直。第三步,在平面ABCD内过点B画直线与A1E垂直。这是已知结论探索条件的问题,借助分析法,A1E是平面ABCD的斜线,在平面ABCD内画直线与A1E垂直可以转化为在平面ABCD内画直线与A1E在平面ABCD内的射影垂直,所以过点B画直线与AC垂直,即为BD。同理画出交线BN,最终画出截面BDHN。
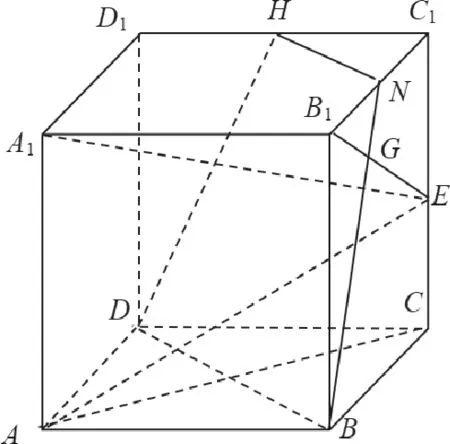
图9
满足条件“BP⊥A1E,BQ⊥A1E”的点P(点Q)的集合构成平面BDHN,同时P、Q均在平面A1B1C1D1内,所以点P(点Q)在两平面的交线HN上,且问题中两直线PQ与BD平行。
【思路2】如图10所示,以D为原点建立空间直角坐标系,过点B与A1E垂直的平面上任取一点M,设点M(x,y,z),设正方体的棱长为1。由A1E⊥BM,求出过点B与A1E垂直的平面对应的方程为。由联立求得x-y=0,由数到形,画出截面与平面xoy的交线BD;同理画出截面与正方体表平面的其它交线从而找到截面BDHN。
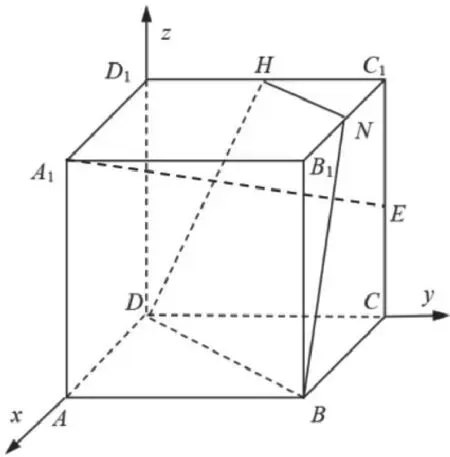
图10
【点评】思路1需要较好的空间想象能力,以及能灵活转化线线垂直与线面垂直的位置关系,思路2相比之下,步骤明确,简单方便。
对于画交线问题,解决方式主要几何法和代数法。几何法是借助直观想象,结合立体几何中的基本事实和定理进行逻辑推理,要注重画交线背后的思路分析。代数法需要数形转化,综合解析几何的知识解决问题。画交线问题培养了学生直观想象、逻辑推理、运算求解等核心素养,教师在教学中值得重视,也是命题的好素材。
