基于主从博弈的输配电网协同经济调度

李本新，刘 振，陈厚合，姜 涛，李 雪，王长江，王昌荣

基于主从博弈的输配电网协同经济调度

李本新1，刘 振1，陈厚合1，姜 涛1，李 雪1，王长江1，王昌荣2

(1.现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学)，吉林 吉林 132012；2.吉林电力股份有限公司松花江热电公司，吉林 吉林 132000)

针对市场环境下如何协调主动配电网与输电网的运行策略以实现二者共赢的问题，提出一种基于主从博弈的输配电网协同经济调度策略。首先，采用主从博弈架构建立了输配电网双层经济调度优化模型，其中上层为输电网价格出清模型，下层为考虑二阶锥交流潮流约束的配电网经济调度模型。然后，应用二阶锥重构技术、KKT (Karush-Kuhn-Tucker)条件、强对偶定理和线性松弛技术将所提双层模型转化为混合整数二阶锥单层规划模型进行求解。最后通过算例验证了模型和方法的有效性。结果表明，所提输配协同经济调度策略可以有效降低输电网电能及备用出清价格，同时提高了配电网运行经济性。

输配协同；经济调度；主动配电网；备用；主从博弈

0 引言

在“双碳”目标驱动下，以新能源为主体的新型电力系统将加速构建[1-2]，配电网与输电网间的耦合互动将愈加频繁，如何协调输配两级电网间的运行策略以提高新能源消纳能力，降低电网运行成本已成为研究的热点问题[3]。

对此，国内外学者进行了诸多相关研究。文献[4]提出了一种基于异构分解的输配电网协同经济调度模型和方法；文献[5]考虑节点边际电价灵敏性，提出了一种基于改进异构分解法的输配协同优化调度方法，进一步提高了算法的收敛性能；文献[6]提出了计及发电机组频率调节效应和负荷电压静态特性的输配协同动态经济调度模型，有效减少了弃风电量；文献[7]基于改进并行子空间算法对输配两级电网进行协同优化；文献[8]提出了一种基于加速增广拉格朗日法的输配电网分布式经济调度协调架构；文献[9]基于交替乘子法构建了输配电网分布式鲁棒经济调度协调决策模型和方法；文献[10]计及风力发电的不确定性，提出一种高比例新能源电力系统输配分层协同优化调度方法；文献[11]考虑主动配电网对输电网的备用容量支撑，构建了集中式分布鲁棒优化调度模型，并应用目标级联法予以分散求解。目前针对输配电网协同运行优化方面的研究更加强调整体利益，多是基于输配一体化经济调度模型开展不同类型的分布式优化方法的研究，较少从不同利益主体的角度开展对输配两级电网协同经济调度策略的研究。

随着电力体制改革的逐步深化[12-13]，配电网将成为电力市场的积极参与者[14-16]，并在特定条件下与输电网构成对立统一的利益关系。在此背景下，设计一种考虑输配电网不同利益的协同经济调度策略以实现二者的共赢就显得非常重要。

针对多利益主体的电力系统经济调度问题，主从博弈作为一种处理不同利益主体复杂经济行为的有效工具获得了广泛应用[17-19]，其在强调整体利益的同时，更关注不同利益主体的个体利益。文献[20]针对配电网风电消纳问题，运用动态主从博弈理论，结合用户负荷特性，同时考虑价格型需求响应的不确定性，提出一种以配电网侧为主体、用户负荷侧为从体的主从博弈模型；文献[21]考虑到增量市场环境下的多供电主体，研究了在外部监管和自由竞

争两种场景下基于主从博弈理论的配电网运营商与用户的电能交易过程；文献[22]提出了基于双层主从博弈、多重激励需求响应思想的微电网群“群-网-荷”一体化利益博弈优化调度策略。上述文献都是基于主从博弈对配电网和用户之间的交互行为进行模拟，尚未涉及输电网与多主动配电网间的均衡博弈过程。

为此，本文在前人工作基础上，假设输配电网所有市场成员均基于成本特性进行报价，基于运行方式进行报量[23-24]，通过模拟市场环境下多主动配电网同时参与输电网能量和备用辅助服务市场的博弈过程，提出了一种基于主从博弈的输配电网双层经济调度模型，用以出清输电网各节点电能和备用的边际价格，并优化配电网的购电和备用服务策略。

1 输配电网主从博弈双层经济调度模型

随着电力市场化改革的不断深入，输电网和主动配电网将成为不同的投资运营主体，为均衡二者不同的利益诉求，本文采用主从博弈架构描述输电系统运营商(Transmission System Operator, TSO)和配电系统运营商(Distribution System Operator, DSO)之间的博弈关系，构建了基于主从博弈的输配电网双层经济调度优化模型，其博弈架构如图1所示。

图1 输电网-配电网主从博弈架构

上层模型中，TSO是制定输-配电网边界节点电能和备用出清价格的领导者。下层模型中，DSO扮演追随者的角色，响应TSO定价并将其购电策略和备用辅助服务策略发送给TSO，TSO据此对电能及备用出清价格进行再调整。当输-配电网边界节点电能和备用出清价格不再改变时，即达到博弈平衡点。

1.1 上层TSO价格出清模型

1.1.1目标函数

上层模型中，TSO根据DSO的购电及备用策略，以输电网总运行成本最小为目标对输-配电网边界节点电能及备用价格进行出清，即

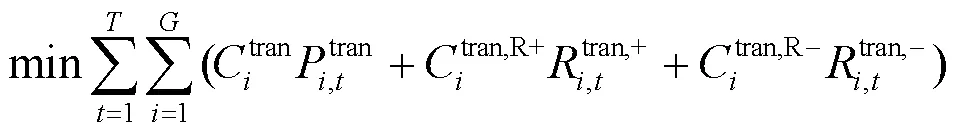
1.1.2约束条件

1) 有功平衡约束

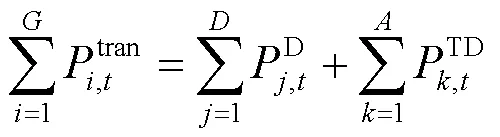
2) 备用约束

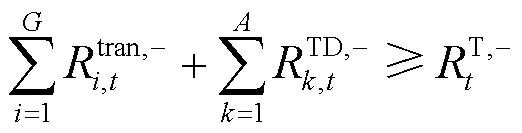
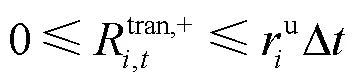
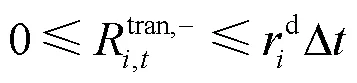
3) 机组功率上、下限约束

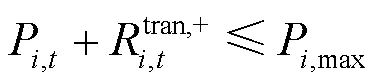
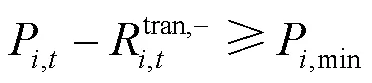
4) 机组爬坡约束

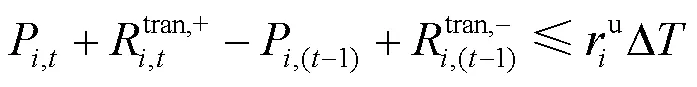
式中，D为一个调度时段的延续时间。

5) 线路潮流约束

1.1.3 输-配电网边界节点电能和备用价格出清

为计算输-配电网边界节点电能及备用的出清价格，本节将式(1)—式(11)所示的TSO价格出清模型转化为等价的对偶形式，如式(12)、式(13)所示。

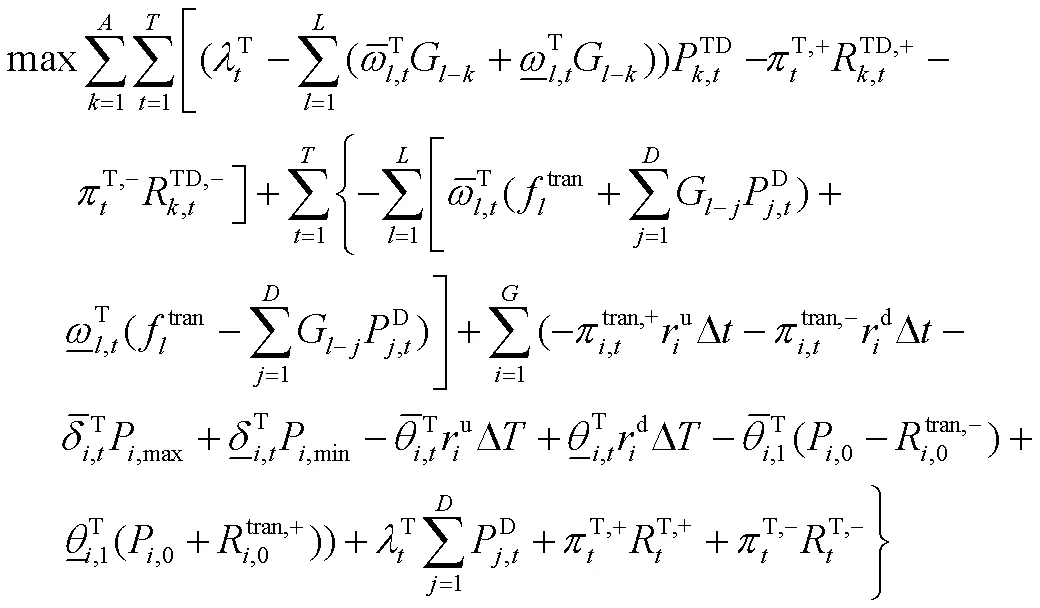
基于上述TSO价格出清对偶模型，参考文献[25]，配电网与输电网边界节点的电能和备用出清价格可表示为

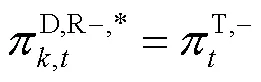
1.2 下层DSO经济调度模型

下层模型中，各配电网基于上层TSO出清的输-配电网边界节点的电能和备用价格优化自身的购电和备用策略，对于第个配电网，其经济调度模型构造如下。

1.2.1目标函数

分布式电源包括可再生能源发电和可控分布式电源，本文忽略风、光等可再生能源发电的运维成本，以配电网运行成本最小为目标，基于上层输电网出清的边界节点的电能和备用价格，优化其可控分布式电源的发电和备用策略，即

1.2.2约束条件

1) 功率平衡约束

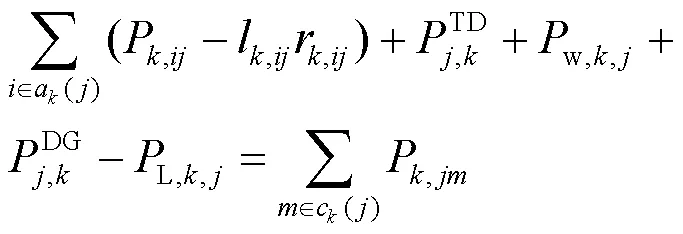
2) 电压降方程和节点电压约束[26]

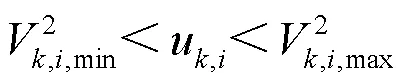
3) 线路潮流约束

借鉴文献[27]，基于二阶锥形式的线路潮流约束可表示为

4) 分布式电源出力上下限约束

5) 备用约束

由于配电系统中的可控分布式电源响应速度快，在一个调度时段内功率可以在上限值和下限值之间自由调节[9]，因此本文忽略分布式电源备用响应的爬坡速率限制。

6) 输配电网耦合支路传输容量约束

2 求解方法

对于所构建的输配电网主从博弈双层优化模型，由于上层价格出清策略与下层主动配电网购电及备用策略相互嵌套，因此难以直接进行求解，同时下层模型中二阶锥形式的线路潮流约束亦加剧了模型求解的困难。对此，本文首先应用二阶锥重构技术[28]和KKT最优性条件[29-32]将主从博弈双层优化模型转化为单层的均衡数学规划模型，然后利用强对偶定理及线性松弛技术将均衡数学规划模型转化为易于求解的混合整数二阶锥规划模型。求解流程如图2所示。

1) 在二阶锥线路潮流约束重构基础上，用KKT条件等效替代下层DSO经济调度模型，并以附加约束条件的形式添加到上层TSO出清模型的对偶问题中，由此将主从博弈双层优化模型转化为单层的均衡约束数学规划模型。

2) 对于转化后均衡约束数学规划模型中的KKT互补松弛约束等非凸约束，应用线性松弛技术对其作线性化处理，转化为凸约束。

3) 为了便于求解，对于转化后均衡约束数学规划目标函数中的非线性项，利用强对偶定理[30]进行线性化处理，使其转化为混合整数二阶锥规划模型，最后通过调用商业求解器CVX /CPLEX进行求解，获得输电网与多主动配电网主从博弈经济调度双层优化模型的均衡解。

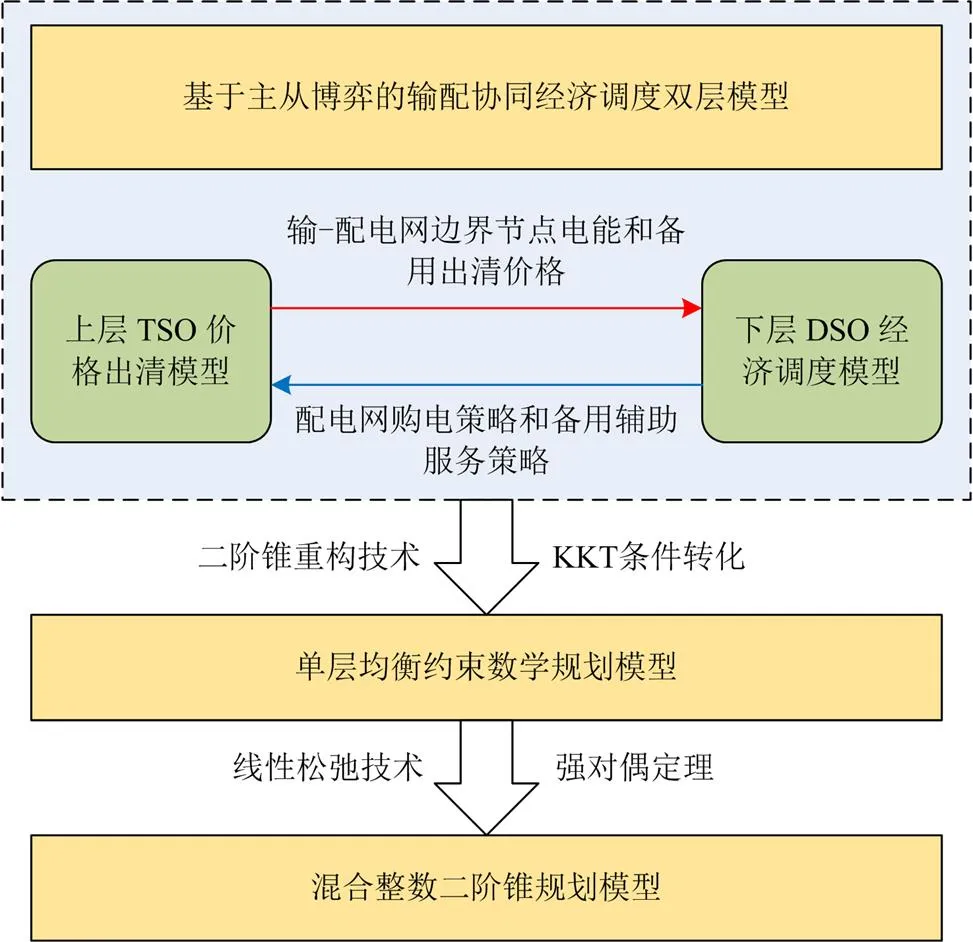
图2 求解过程示意图

3 算例分析

本节分别采用T6D2系统和T118D10系统来验证本文所提模型和方法的有效性。

3.1 T6D2系统

3.1.1算例介绍

如图3所示，T6D2系统由1个6节点输电网与2个配电网构成，其中配电网1和配电网2分别经边界节点B3、B4与输电网联结，系统各时段的总负荷、各时段输电网和配电网的上调(下调)备用需求见图4、图5，机组参数在文献[33]的基础上略作修改，见表1。

为说明本文所提模型和方法的有效性，设置以下3种场景。

场景1：不考虑输配电网之间的博弈，将配电网视为固定负荷且不向输电网提供备用支撑。该场景下，风电按预测值出力，其他分布式电源出力设为0。

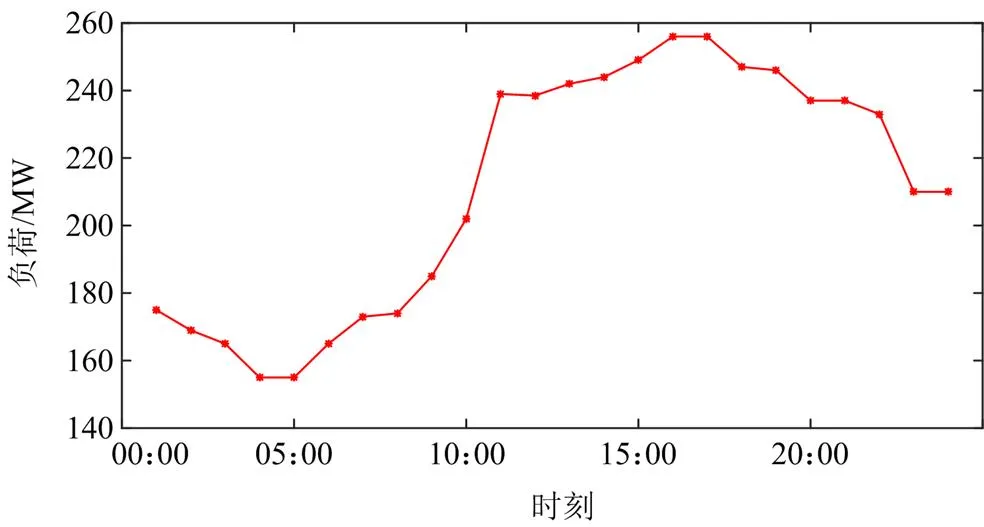
图3 T6D2测试系统

图4 系统总负荷

图5 各时段输电网和各配电网的备用需求

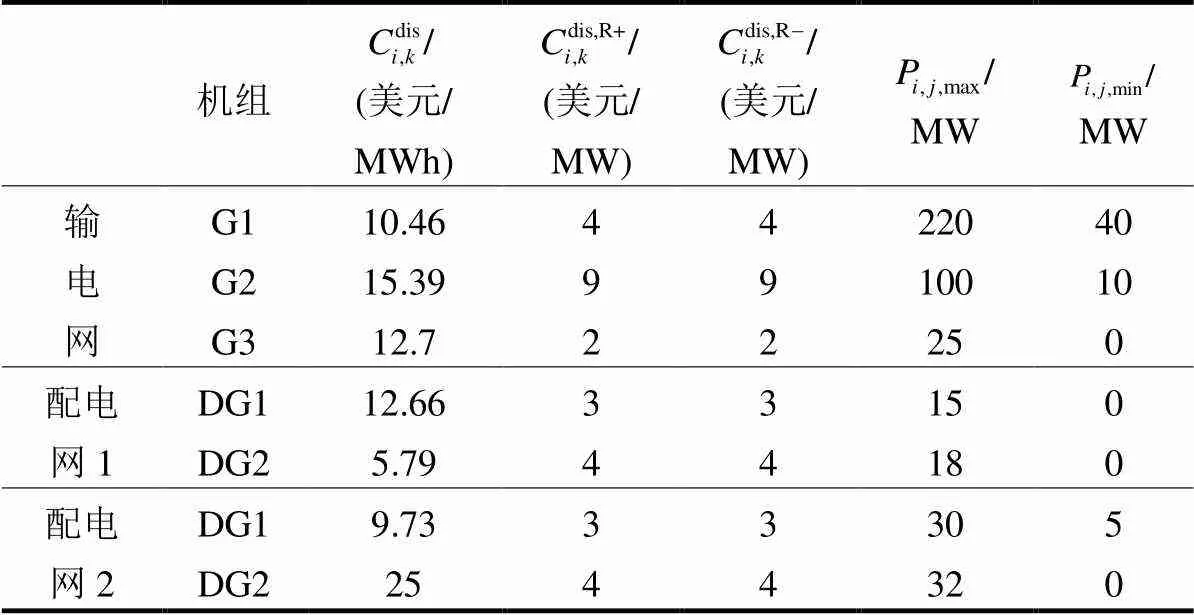
表1 T6D2系统各机组数据

场景2：仅考虑输配电网间交互的有功功率博弈，配电网中分布式电源不向输电网提供备用支撑，仅提供配电网自身所需备用。

场景3：输配两级电网之间有功功率和备用同时博弈，即配电网分布式电源在主动参与输电网有功平衡的同时，也考虑为其提供备用辅助服务。

3.1.2结果分析

1) 配电网运行策略对电能出清价格影响分析。

本节以边界节点B3为例分析配电网购电和备用辅助服务策略对电能出清价格的影响。图6给出了3种场景下边界节点B3的电能出清价格。图7给出了3种场景下输电网各机组出力情况(同一时段下的3组数据分别对应场景1、场景2和场景3，“剩余出力”表示各机组实际出力与机组最小技术出力之差)；图8给出了3种场景下各配电网的购电策略(同一时段下的3组数据分别对应3种场景)；图9给出了场景2、场景3下输配电网各机组所提供的上调备用(同一时段下的两组数据分别为场景2、场景3)。

由图6、图7可以看出，01：00—10：00时段、23：00—24：00时段由于负荷较低，3种场景下节点B3的电能出清价格一致，均为10.46美元/MWh，在11：00—14：00时段、20：00—22：00时段，随着用电负荷的增加，场景1中报价较低的G1机组满发，机组G3变为边际机组，由此使节点B3电能出清价格上升为12.7美元/MWh，在15：00—19：00时段，随着负荷进一步增加，机组G1、G3均满发，报价较高的机组G2变为边际机组，从而使节点B3电能出清价格进一步上升为15.39美元/MWh。结合图8可以看出，场景2由于配电网分布式电源参与了输电网有功平衡，降低了配电网的购电功率，间接减少了输电网报价较高机组出力，使场景2在10：00—15：00时段、18：00—22：00时段的边际机组仍为G1，电能出清价格保持10.46美元/MWh不变，而16：00—17：00时段由于负荷达到峰值，此时机组G1满发，机组G3成为了边际机组，节点B3电能出清价格小幅度上升至12.7美元/MWh，但仍低于场景1的出清价格。可见，考虑配电网主动参与输电网有功平衡能减少输电网报价较高机组输出功率，降低输电网电能出清价格。

图6 3种场景下节点B3出清电价

图7 3种场景下输电网各机组出力

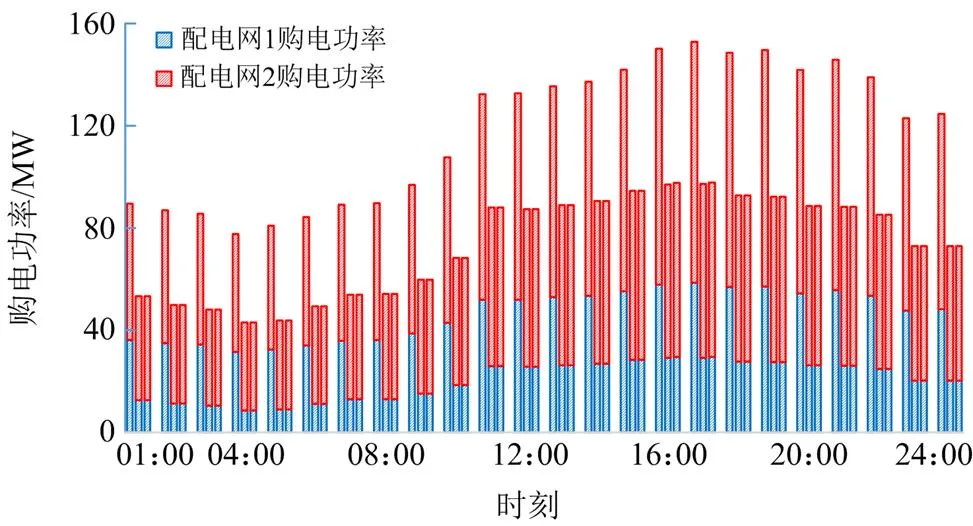
图8 3种场景下各配电网的购电功率

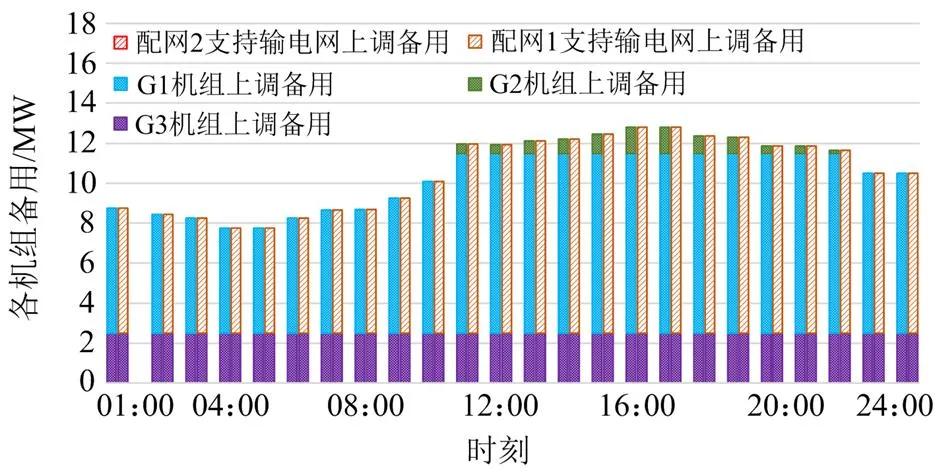
图9 场景2、场景3下各机组所提供的上调备用容量

对比场景2和场景3，由图6、图9可知，在16：00—17：00时段，由于场景3下配电网向输电网提供备用支撑，输电网电能报价较低机组G1不再提供备用，而是将该部分容量用于发电，使边际机组由场景2下的G3变为G1，节点B3的电能出清价格由场景2的12.7美元/MWh下降为10.46美元/MWh。可见，考虑配电网向输电网提供备用支撑能够降低对输电网机组的备用负担，使经济性较好的机组更多地用于发电，从而降低输电网的电能出清电价。

2) 配电网运行策略对备用出清价格影响分析。

本节以上调备用为分析对象研究配电网运行策略对备用出清价格的影响。图10给出了场景2、场景3下系统的上调备用出清电价。

图10 场景2、场景3下的上调备用出清价格

由图10可知，01：00—24：00时段，场景2的上调备用出清价格均高于场景3的上调备用的出清电价。结合图9可以看出，在01：00—10：00时段和23：00—24：00时段，场景2下输电网所需上调备用均由机组G1、G3承担，其中G1机组为备用边际机组，此时上调备用的出清价格为G1的上调备用报价，而在11：00—22：00时段，G1、G3机组所提供的备用达到其上限值，此时G2机组成为了备用边际机组；对于场景3，在01：00—24：00时段，配电网向输电网支持备用，此时备用的边际机组由输电网的G1机组变成了配电网1中更加经济的分布式电源机组，从而使该场景备用出清价格低于场景2的备用出清价格。可见，配电网参与输电网备用辅助服务市场博弈，能够降低输电网中备用报价较高机组所承担的备用，提高配电网中分布式电源的利用率，有效降低系统备用出清价格。

3) 输配电网主从博弈策略对电网运行经济性的影响分析。

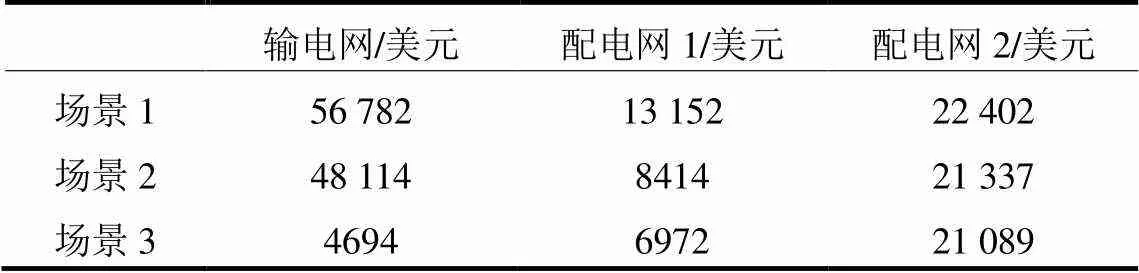
表2 3种场景下T6D2系统运行成本

表2给出了3种场景下T6D2系统输电网和各配电网的运行成本。可以发现：相较于场景1，场景2中输电网的运行成本由56 782美元下降到48 114美元，这是由于配电网主动参与输电网有功平衡博弈后，分布式电源在输-配边界节点价格信号引导下增发有功功率，从而使输电网机组有功出力减少，引起输电网运行成本降低。与此同时，配电网1(2)的运行成本也由场景1的13 152美元(22 402美元)减少为场景2的8414美元(21 337美元)，一方面是由于配电网参与输电网有功平衡后有效降低了输配电网边界节点的出清价格，即降低了配电网从输电网购买电能的价格；另一方面是由于配电网中较为经济的分布式电源响应价格信号增发有功功率，降低了配电网以较高电价从输电网购买的电量。

相较于场景2，场景3中由于考虑了配电网向输电网提供备用支撑，降低了输电网中机组的备用负担，使电能报价较低机组G1在16：00—17：00时段的备用容量转而用于发电，由此使场景3下输电网的运行成本进一步下降到46 194美元。此外，相对于场景2，场景3中由于16：00—17：00时段配电网向输电网购电价格的降低以及配电网向输电网提供备用所获得的收益，使得场景3下配电网1(2)的运行成本进一步减少为6972美元(21 089美元)。可见，主动配电网同时参与输电网的有功和备用博弈，可以有效降低输配电网运行成本。

3.2 T118D10系统

由于输配电网实际系统算例数据难以获得，为验证本文所提模型和方法在大系统算例中的有效性，构造T118D10系统予以分析说明。T118D10测试系统是由1个IEEE118节点的输电网与5个PG&E69节点[34]的主动配电网以及5个改进的IEEE33节点主动配电网组成。其中输电网的节点18、32、34、40、55[35]各连接一个69节点配电网；节点70、74、77、92和112分别连接一个33节点配电网。IEEE118节点的输电网和IEEE33节点的配电网数据详见http://motor.ece.iit.edu/data，并假设输电网各机组按最大技术出力对应的平均成本报价；69节点配电网和33节点配电网机组参数详见表3。

表3 69节点和33节点配电网机组数据

本节继续沿用3.1节设置的3种场景分析输配电网主从博弈策略对电网运行经济性影响。表4给出了3种场景下T118D10系统的运行成本，可以发现，输电网及各配电网在场景1、场景2和场景3的运行成本依次降低，进一步地验证了本文所提基于主从博弈的输配电网经济调度双层优化模型的有效性。

表4 3种场景下T118D10系统运行成本

为了说明本文所提方法的优越性，本节采用基于异构分解法(Heterogeneous Decentralized algorithm, HGD)[4]的模型求解方法与本文所提基于KKT条件的优化方法进行对比。

表5给出了基于HGD和KKT不同方法计算的T118D10系统的运行成本。可以发现，两种算法优化得到的各输配电网的运行成本相近，以HGD算法优化结果为基准的相对偏差均在0.1%以下，且基于KKT条件计算的各输配电网运行成本略小于HGD算法的优化结果，也就是说，本文基于KKT条件的双层模型求解方法能够更有效地找到输配电网主从博弈双层经济调度模型的最优均衡解。

表5 基于HGD和KKT条件计算的T118D10系统运行成本

此外，采用HGD算法求解时，输配电网需要交替迭代3次，计算耗时为47 min, 而采用KKT条件的优化方法计算时间为3.2 min。即基于KKT条件的双层模型优化方法所需时间要远小于HGD算法，这是由于采用HGD算法时，每次迭代过程均需对每一个主动配电网进行一次电网潮流分析以得到交互迭代量，由于配电网模型采用交流潮流模型，故每次迭代的时间较长。而本文所提的基于KKT条件的双层模型优化算法可以将模型转化为单层混合整数二阶锥规划模型，无需迭代，从而大大地减少了计算时间。

4 结论

本文在主从博弈框架下描述输电网和主动配电网间的交互关系，提出一种基于主从博弈的输配协同经济调度双层优化模型和方法，经分析验证结论如下。

1) 相比于传统输配分离调度模式，本文所提基于主从博弈的输配协同经济调度策略可以有效地降低输电网电能及备用的出清价格。

2) 主动配电网同时参与电能及备用辅助服务，不仅能够提高分布式电源的利用率，降低配电网的运行成本，也能提高输电网运行经济性。

3) 采用了基于KKT条件的双层模型优化算法能够有效避免传统双层模型求解算法繁琐的交叉迭代过程，提高计算效率。

未来工作将进一步考虑风电预测概率特性对主从博弈架构下输配协同经济调度的影响，进一步提升新能源消纳能力。

[1] 李军徽, 冯喜超, 严干贵, 等. 高风电渗透率下的电力系统调频研究综述[J]. 电力系统保护与控制, 2018, 46(2): 163-170.

LI Junhui, FENG Xichao, YAN Gangui, et al. Survey on frequency regulation technology in high wind penetration power system[J]. Power System Protection and Control, 2018, 46(2): 163-170.

[2] Zhang D, Li J, Hui D. Coordinated control for voltage regulation of distribution network voltage regulation by distributed energy storage systems[J]. Protection and Control of Modern Power Systems, 2018, 3(1): 35-42.

[3] Calum E, Stuart G, Ian E, et al. Design of a DSO-TSO balancing market coordination scheme for decentralized energy[J]. IET Generation, Transmission & Distribution, 2020, 14(5): 707-718．

[4] Li Z, Guo Q, Sun H, et al.Coordinated economic dispatch of coupled transmission and distribution systems using heterogeneous decomposition[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4817-4830.

[5] LI Z, GUO Q, SUN H, et al. A new LMP-sensitivity- based heterogeneous decomposition for transmission and distribution coordinated economic dispatch[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 931-941.

[6] Du P, Zhao Q, Deng H, et al. Bi-level distributed day ahead economic dispatch model of transmission and distribution networks[C] // 2020 International Conference on Electrical Engineering and Control Technologies (CEECT),December 10-13, 2020, Melbourne, VIC, Australia.

[7] 叶畅, 苗世洪, 李超, 等. 基于改进并行子空间算法的输配两级电网协同优化[J]. 电工技术学报, 2018, 33(23): 5509-5522.

YE Chang, MIAO Shihong, LI Chao, et al. Coordination optimal scheduling strategy for transmission and distribution system based on improved CSSO algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5509-5522.

[8] Arpanahi M K, Golshan M E H, Siano P. A comprehensive and efficient decentralized framework for coordinated multiperiod economic dispatch of transmission and distribution systems[J]. IEEE Systems Journal, 2021, 15(2): 2583-2594.

[9] Chen Z, Guo C, Dong S, et al. Distributed robust dynamic economic dispatch of integrated transmission and distribution systems[J]. IEEE Transactions on Industry Applications, 2021, 57(5): 4500-4512.

[10] 张旭, 王洪涛. 高比例可再生能源电力系统的输配协同优化调度方法[J]. 电力系统自动化, 2019, 43(3): 67-83, 115.

ZHANG Xu, WANG Hongtao. Optimal dispatch method of transmission and distribution coordination for power systems with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2019, 43(3): 67-75, 115.

[11] Li P, Wu Q, Yang M, et al. Distributed distributionally robust dispatch for integrated transmission-distribution systems[J]. IEEE Transactions on Power Systems, 2021, 36(2): 1193-1205.

[12] 关于进一步深化电力体制改革的若干意见(中发[2015] 9号文) [EB/OL]. [2015-03-15]. https://smartgrids.of week. com/2015-03/ART-290010-8480-28942130.html．

[13] 何黎君, 程杉, 陈梓铭. 考虑交互功率控制和双边竞价交易的多微电网双层优化调度[J]. 电力系统保护与控制, 2020, 48(11): 10-17.

HE Lijun, CHENG Shan, CHEN Ziming. A scheduling model of a multi-microgrid system based on bi-layer optimization with consideration of PCC power control and bilateral bidding[J]. Power System Protection and Control, 2020, 48(11): 10-17.

[14] 艾欣, 陈炜. 考虑容量管理的主动配电网市场化实时竞价运营模式[J]. 中国电机工程学报, 2014, 34(22): 3743-3749.

AI Xin, CHEN Wei. Marketization real-time bidding operation mode of the active distribution network with consideration of capacity management[J]. Proceedings of the CSEE, 2014, 34(22): 3743-3749.

[15] 朱洪强, 王磊. 增量配电网发展前景分析[J]. 科学技术创新, 2019(32): 165-166．

ZHU Hongqiang, WANG Lei. Analysis of development prospect of incremental distribution network[J]. Scientific and Technological Innovation Information, 2019(32): 165-166.

[16] 国家电网公司. 国家电网公司发布进一步支持和推进增量配电业务改革的意见[EB/OL]. [2020-03-01]. http://www.js.sgcc.com.cn/html.

[17] Wu T, Rothleder M, Alaywan Z, et al. Pricing energy and ancillary services in integrated market systems by an optimal power flow[J]. IEEE Transactions on Power Systems, 2004, 19(1): 339-347.

[18] Mei S, Wang Y, Liu F, et al. Game approaches for hybrid power system planning[J]. IEEE Transactions on Sustainable Energy, 2012, 3(3): 506-517.

[19] Mei S, Zhang D, Wang Y, et al. Robust optimization of static reserve planning with large scale integration of wind power: a game theoretic approach[J]. IEEE Transactions on Sustainable Energy, 2014, 5(2): 535-545.

[20] 邱革非, 何超, 骆钊, 等. 考虑新能源消纳及需求响应不确定性的配电网主从博弈经济调度[J]. 电力自动化设备, 2021, 41(6): 66-74.

QIU Gefei, HE Chao, LUO Zhao, et al. Economic dispatch of Stackelberg game in distribution network considering new energy consumption and uncertainty of demand response[J]. Electric Power Automation Equipment, 2021, 41(6): 66-74.

[21] 刘源, 潘雪莉, 杨军, 等. 增量市场环境下多供电主体市场博弈模型与交易行为分析[J]. 电力自动化设备, 2019, 39(12): 162-168.

LIU Yuan, PAN Xueli, YANG Jun, et al. Market game model and trading behavior analysis of multiple power supply agents in increment electricity market[J]. Electric Power Automation Equipment, 2019, 39(12): 162-168.

[22] 林凯骏, 吴俊勇, 刘迪, 等. 基于双层Stackelberg博弈的微能源网能量管理优化[J]. 电网技术, 2019, 43(3): 973-983.

LIN Kaijun, WU Junyong, LIU Di, et al. Energy management optimization of micro energy grid based on hierarchical Stackelberg game theory[J]. Power System Technology, 2019, 43(3): 973-983.

[23] 刘聪, 周京阳, SHAHIDEHPOUR M, 等. 市场环境下输配电系统一体化分布式交易优化方法[J]. 电力系统自动化, 2019, 43(21): 103-110.

LIU Cong, ZHOU Jingyang, SHAHID EHPOUR M, et al. Optimization method for decentral transaction of integrated transmission and distribution system in market environment[J]. Electric Power Automation Equipment, 2019, 43(21): 103-110.

[24] Jabr R A, Singh R, Pal B C. Minimum loss network reconfiguration using mixed-integer convex programming[J]. IEEE Transactions on Power Systems, 2012, 27(2): 1106-1115.

[25] 史新红, 郑亚先, 薛必克, 等. 机组运行约束对机组节点边际电价的影响分析[J]. 电网技术, 2019, 43(8): 2658-2665.

SHI Xinhong, ZHENG Yaxian, XUE Bike, et al. Effect analysis of unit operation constraints on locational marginal price of unit nodes[J]. Power System Technology, 2019, 43(8): 2658-2665.

[26] 张蕊, 李铁成, 李晓明, 等. 考虑设备动作损耗的配电网分布式电压无功优化[J]. 电力系统保护与控制, 2021, 49(24): 31-40.

ZHANG Rui, LI Tiecheng, LI Xiaoming, et al. Distributed optimization for distribution networks volt/var control considering the operation cost of equipment[J]. Power System Protection and Control, 2021, 49(24): 31-40.

[27] 刘一兵, 吴文传, 张伯明, 等. 基于混合整数二阶锥规划的三相有源配电网无功优化[J]. 电力系统自动化, 2014, 38(15): 58-64.

LIU Yibing, WU Wenchuan, ZHANG Boming, et al. Reactive power optimization for three-phase distribution networks with distributed generators based on mixed integer second-order cone programming[J]. Automation of Electric Power Systems, 2014, 38(15): 58-64.

[28] Stephen B, Lieven V. Convex optimization[M]. Cambridge: Cambridge University Press, 2004: 93-97.

[29]白浩, 袁智勇, 周长城, 等. 计及新能源波动与相关性的配电网最大供电能力调度方法[J]. 电力系统保护与控制, 2021, 49(8): 66-73.

BAI Hao, YUAN Zhiyong, ZHOU Changcheng, et al. Dispatching method of maximum power supply capacity of a power distributed network considering fluctuation and correlation of renewable energy[J]. Power System Protection and Control, 2021, 49(8): 66-73.

[30] 张立辉, 戴谷禹, 聂青云, 等. 碳交易机制下计及用电行为的虚拟电厂经济调度模型[J]. 电力系统保护与控制, 2020, 48(24): 154-163.

ZHANG Lihui, DAI Guyu, NIE Qingyun, et al. Economic dispatch model of virtual power plant considering electricity consumption under a carbon trading mechanism[J]. Power System Protection and Control,2020, 48(24): 154-163.

[31] 陈厚合, 何旭, 姜涛, 等. 计及可中断负荷的电力系统可用输电能力计算[J]. 电力系统自动化, 2017, 41(15): 81-87, 106.

CHEN Houhe, HE Xu, JIANG Tao, et al. Available transfer capability calculation of power systems considering interruptible load[J]. Automation of Electric Power Systems, 2017, 41(15): 81-87, 106.

[32] 陈厚合, 吴桐, 李本新, 等. 考虑建筑热惯性的园区代理商电价策略及用能优化[J]. 电力系统自动化, 2021, 45(3): 148-156.

CHEN Houhe, WU Tong, LI Benxin, et al. Electricity pricing strategy of park retailer and energy optimization considering thermal inertia of building[J]. Automation of Electric Power Systems, 2021, 45(3): 148-156.

[33] Kargarian A, Fu Y. System of systems based security constrained unit commitment incorporating active distribution grids[J]. IEEE Transactions on Power Systems, 2014, 29(5): 2489-2498.

[34] Savier J S, DASD. Impact of network reconfiguration on loss allocation of radial distribution systems[J]. IEEE Transactions on Power Delivery, 2007, 22(4): 2473-2480.

[35] Chen Z, Li Z, Guo C, et al. Fully distributed robust reserve scheduling for coupled transmission and distribution systems[J]. IEEE Transactions on Power Systems, 2021, 36(1): 169-182.

Collaborative economic dispatch of coupled transmission and distribution networks based on the Stackelberg game

LI Benxin1, LIU Zhen1, CHEN Houhe1, JIANG Tao1, LI Xue1, WANG Changjiang1, WANG Changrong2

(1. Key Laboratory of Modern Power System Simulation and Control & Renewable Energy Technology, Ministry of Education (Northeast Electric Power University), Jilin 132012, China; 2. Songhuajiang Thermal Power Generation Co., Ltd., Jilin Electric Power Co., Ltd., Jilin 132000, China)

There is a problem of how to coordinate the operation strategy of coupled transmission and distribution networks to achieve a win-win situation in the market environment. Thus a cooperative economic dispatch strategy of coupled transmission and distribution networks based on the Stackelberg game is proposed. First, a bi-level optimization model is established to solve the economic dispatch of coupled transmission and distribution networks using Stackelberg game architecture, in which the upper level is the transmission network price clearing model and the lower level is the economic dispatch model of each distribution network. This considers second order cone alternating current power flow constraints. Then, the second order cone reconstruction technique, KKT (Karush-Kuhn-Tucker) conditions, strong duality theorem and linear relaxation technique are applied to transform the proposed bi-level model into a mixed integer second-order cone programming single-layer model for analysis. Finally, the simulations verify the effectiveness of the proposed model and method. The results show that the proposed cooperative economic dispatch strategy can effectively reduce the clearing price of transmission energy and reserve, and reduce the operational cost of the distribution networks.

coordination of transmission and distribution networks; economic dispatch; active distribution network; reserve; Stackelberg game

10.19783/j.cnki.pspc.211714

2021-12-15；

2022-02-23

李本新(1987—)，男，博士，讲师，硕士生导师，研究方向为电力系统运行与控制；E-mail: benxinli@163.com

刘 振(1995—)，男，硕士研究生，研究方向为电力系统经济运行；E-mail: zhenliu12138@aliyun. com

陈厚合(1978—)，男，教授，博士生导师，研究方向为电力系统安全性与稳定性等。E-mail: chenhouhe@126.com

吉林省科技发展计划项目资助(20210508031RQ)

This work is supported by the Science and Technology Project of Jilin Province (No. 20210508031RQ).

(编辑 许 威)