一种基于S_VMD与Sdr_SampEn的局部放电信号去噪方法

马星河，孔卫东，李自强，王琬凇，鲍靖雯

一种基于S_VMD与Sdr_SampEn的局部放电信号去噪方法

马星河1,2，孔卫东1，李自强3，王琬凇4，鲍靖雯5

(1.河南理工大学电气工程与自动化学院，河南 焦作 454000；2.河南省煤矿装备智能检测与控制重点实验室，河南 焦作 454000；3.许继电气股份有限公司，河南 许昌 461000；4.南京大全电气有限公司，江苏 南京 211106；5.河南平高电气股份有限公司，河南 平顶山 467000)

交联聚乙烯(XLPE)电缆作为“双碳”目标中电力传输的重要工具，在使用一定年限后绝缘性能会下降，局部放电(Partial Discharge, PD)检测作为评估XLPE电缆绝缘状态的重要手段已广泛应用。针对PD信号中存在的各类噪声问题，提出了一种基于Spearman变分模态分解(Spearman Variational Mode Decomposition, S_VMD)与空间相关递归样本熵(Spatial Dependence Recurrence Sample Entropy, Sdr_SampEn)的局部放电信号去噪方法。首先通过S_VMD将信号分解为个最优本征模态分量(Intrinsic Mode Function，IMF)，然后通过计算各IMF的Sdr_SampEn值来判定其是噪声主导分量还是PD主导分量；再对分类后的IMF分别采取改进小波阈值去噪和Savitzky-Golay (SG)滤波去噪，最后进行重构得到去噪后的PD信号。利用该方法对仿真与实测PD信号进行去噪处理，并与自适应变分模态分解(Adaptive VMD, AVMD)等去噪算法进行对比分析，结果表明该方法能有效抑制PD信号中的噪声，具有一定的工程价值。

交联聚乙烯电缆；局部放电；Spearman相关系数；变分模态分解；空间相关递归样本熵

0 引言

交联聚乙烯(XLPE)电缆作为能源转型措施中电力传输的重要工具，具有不可替代的作用。但是XLPE电缆在使用一定的年限后往往会发生一系列的绝缘故障[1-2]，造成重大经济损失，因此需要对电缆进行绝缘监测，确保其正常运行。

局部放电(Partial Discharge, PD)法作为电缆绝缘检测技术的重要手段之一，广泛应用于各种电缆在线监测设备。但通常情况下PD信号十分微弱，且在现场环境中存在大量的白噪声和周期窄带干扰[3]。这使得纯净PD信号易被噪声淹没，对监测工作造成困扰。因此，对各类噪声的抑制是提高PD信号检测精度的重要一环。

近年来，许多学者提出了去除PD信号中噪声的方法，常见的去噪算法有奇异值分解(Singular Value Decomposition, SVD)算法[4-7]、自适应滤波算法[8-9]、小波变换法[10-13]和经验模态分解(Empirical Mode Decomposition, EMD)算法[14-15]等。SVD算法通过选取合适的奇异值阈值将含噪信号的奇异值进行分类，实现了噪声的抑制，但阈值的选取十分困难。自适应滤波算法对周期窄带干扰十分敏感，但在现场环境中的干扰频率不一致，滤波效果不稳定。小波变换法对白噪声的抑制效果十分明显，但这与基函数和分解层数的选取密切相关，自适应较差。EMD算法无需人工选择基函数，有效地解决了小波变换法自适应不强的问题，但在分解时需要经过多次迭代，计算量大，存在模态混叠和端点畸变等问题[16]。随着研究的深入，集合经验模态分解(Ensemble EMD, EEMD)算法、完全集合经验模态(Complete Ensemble EMD, CEEMD)算法以及各种EMD的改进算法出现在人们的视野中[17-18]。虽然这些算法取得了一定的成效，但未从根本上解决EMD算法固有的缺陷，尤其是模态混叠问题。变分模态分解(Variational Mode Decomposition, VMD)是在传统维纳滤波的基础上提出来的[19]，具有优秀的噪声鲁棒性，既解决了小波分解自适应较差的问题，也改善了EMD算法中出现的模态混叠现象，在非线性信号处理领域得到了广泛的应用。但VMD算法的分解效果受惩罚因子和分解层数的影响较大。在多数研究中，和的选取依靠人为经验，严重影响了分解的效果，甚至会出现欠分解和过分解的现象。此外，文献[20-21]对于模态分解后的非PD分量均采取直接剔除的方法，不参与重构。但文献[22]指出高噪声分量中也包含部分真实信息，不可直接剔除。

除了上述方法外，熵作为一种度量时间序列复杂性的方法也广泛应用于非线性信号平稳性的评价，如近似熵、排列熵[18]等。但近似熵在计算过程中过度依赖数据的长度，排列熵在计算时未考虑到信号幅值之间的关系。样本熵(Sample Entropy)作为一种量化信号不规则性的常见方法，具有抗噪声干扰能力强、计算速度快等特点，但没有考虑到信号的序列信息。文献[23]的空间相关递归样本熵(Spatial Dependence Recurrence Sample Entropy, Sdr_SampEn)可以捕获信号的序列信息，能够对算法分解出的分量进行准确的鉴别，确定其所属类别。

针对以上问题，提出了一种基于S_VMD与Sdr_SampEn的局部放电信号去噪方法。通过Spearman相关系数对VMD算法中的进行优化，确定最优的值，再对含噪信号进行VMD分解。通过计算各IMF的Sdr_SampEn值，判别该IMF是PD主导分量还是噪声主导分量。对于PD主导分量，采取SG平滑滤波的处理[24]，去除信号中残余的微小噪声；对于噪声主导分量利用改进小波阈值法进行去噪，保留分量中的少部分有用信息。对处理后的两类信号进行重构，得到去噪后的PD信号。通过仿真PD信号与实测PD信号的分析，与自适应变分模态分解(Adaptive VMD, AVMD)去噪方法[3]、CEEMD- EEMD去噪方法[17]、广义S变换奇异值分解(S-SVD)去噪方法[25]进行对比，结果表明本文所提去噪方法能有效抑制PD信号中的噪声，且各类去噪指标均优于上述3种去噪方法。

1  基本理论

1.1 斯皮尔曼变分模态分解

VMD是种自适应求解的、非递归的信号处理方式，尤其对于非线性非平稳信号，效果更明显。VMD算法的核心在于变分求解，即通过不断迭代来确定各个IMF的中心频率与带宽，在使各个IMF估计带宽之和最小的情况下，将信号分解成个分量。算法中的参数和至关重要，决定了算法分解出IMF的个数，决定了IMF的频带衰减速率。当较大时，分解速率过快，使得相邻IMF之间的有效部分会被过度去除；当较小时，会出现明显的频带混叠现象。文献[26]指出，当取2000时，自适应效果最佳，去噪效果最理想。对于参数，本文利用Spearman相关系数来确定的最优值[27]。

1.2 空间相关递归样本熵

Sdr_SampEn在计算时可以获取信号的序列信息，对于区分IMF的类型具有十分明显的效果。具体求解过程如下。

图1 最优参数K的确定流程

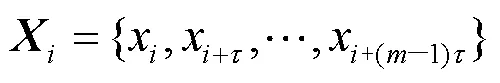
构建相空间的递归矩阵如式(2)所示。

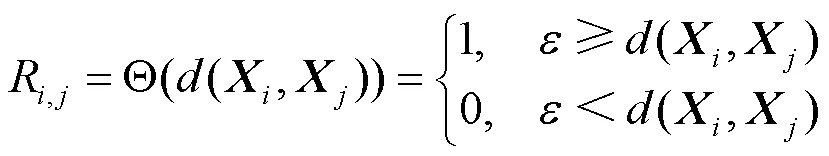
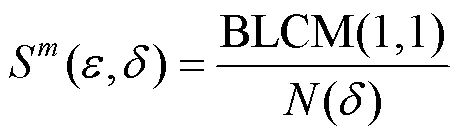
综上，Sdr_SampEn法可以在切比雪夫距离与空间方向两个标准下衡量时间序列的不规则性，如式(5)所示。

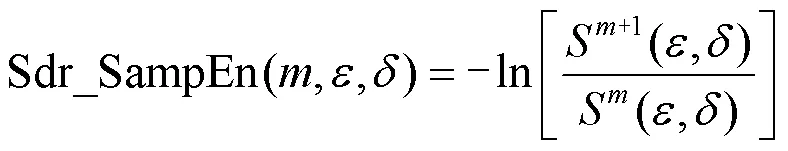
计算Sdr_SampEn的步骤如下：

2) 通过切比雪夫距离得出递归图；

1.3 改进小波阈值去噪与Savitzky-Golay滤波

对于噪声主导分量，本文采取小波阈值去噪的方法进行处理。小波变换的思想是对含噪信号进行小波变换，得到一组小波系数，然后选取合适的阈值，对各层小波系数进行相应的筛选变换，最后对处理后的小波系数进行重构。在整个小波变换的过程中，小波阈值的确定和阈值函数的选取对最终的去噪效果影响极大。本文提出了一种新型的小波阈值去噪方法，阈值函数如式(6)所示。

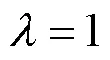
图3 软硬阈值函数与改进阈值函数的对比

对于PD主导分量，本文采取SG滤波去噪。SG滤波也称最小二乘原理的多项式平滑滤波，是一种时域类型的滤波。这种方式被广泛用于数据流的平滑去噪，可以在保证信号形态不变的情况下，对噪声进行滤除。具体方法是先选取一个滑动窗口，接着用一元多阶多项式对数据进行拟合，该多项式的系数可根据最小二乘法准则来确定。最后窗口沿着最佳的拟合值滑动，达到去噪的效果。

2  本文提出的去噪算法

2.1 参数的确定

由第1节所述原理可知，本文还需确定两个关键的参数，一是VMD算法中经Spearman相关系数优化后的，二是Sdr_SampEn算法中区分噪声主导分量和PD主导分量的阈值。

对于参数，根据图1的流程，进行大量仿真实验后，可得到值与Spearman相关系数的关系,如图4所示。

图4 K与Spearman相关系数的关系

为了使阈值更具代表性，本文选取正弦信号与混沌洛伦兹信号进行模拟，由式(7)和式(8)实现。

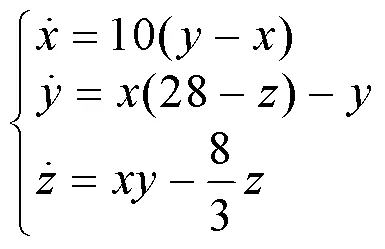
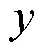
图5 含噪声的正弦信号与混沌洛伦兹信号

由图5可知，当两种含噪信号的信噪比低于0 dB时，两种信号的波形均埋没在噪声中，无法辨别其特征信息。当信噪比大于0 dB时，信号的部分特征才有所显现。因此取信噪比为0 dB时的Sdr_SampEn值为阈值，并作为区分噪声主导分量与PD主导分量的指标。在两种信号中加入-10 dB到20 dB的高斯白噪声，步长取1 dB，每个步长测试20次，求得其Sdr_SampEn的平均值，得到如图6所示的关系图。

图6 含噪声正弦信号与混沌洛伦兹信号的Sdr_SampEn值

图7 本文去噪方法流程图

2.2 去噪评价标准

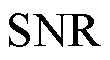
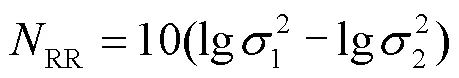
3  仿真信号分析

3.1 PD信号仿真模型

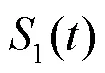
仿真中设置采样频率为50 MSa/s，采样时间为40 µs，得到纯净PD信号如图8(a)所示。在此基础上再加入信噪比为-1 dB的高斯白噪声和周期窄带干扰，其中周期窄带干扰是由不同频率、不同幅值的正弦信号产生，如式(15)所示。叠加噪声后的波形如图8(b)所示，可以看出，原始PD信号已经完全被噪声淹没，无法识别。

式中：为幅值；为频率；为初相角。具体取值如表1所示。

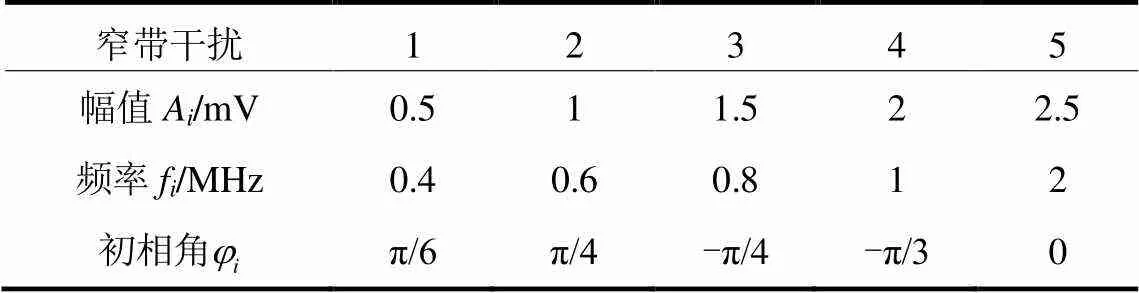
表1 窄带干扰参数设置

3.2 仿真PD信号去噪

由图7可知，首先对含噪PD信号进行S_VMD分解，分解后的IMF1—IMF7如图9所示，其Sdr_ SampEn值如表2所示。

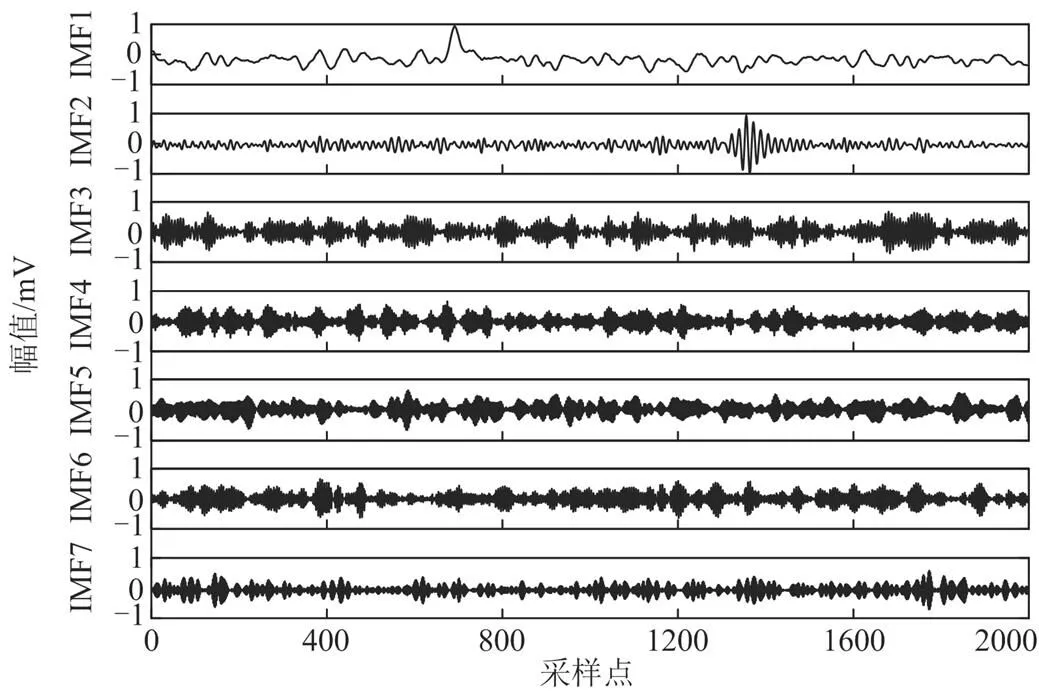
图9 S_VMD分解

表2 IMF的Sdr_SampEn值

由表2可知，IMF1、IMF2、IMF7的Sdr_SampEn值均小于1.94，属于PD主导分量。其中IMF7的Sdr_SampEn值相对于IMF1和IMF2有很大差距，说明IMF1和IMF2中所包含的PD信息更多，其具有PD主导分量的特征较IMF7也更加明显。其余IMF的Sdr_SampEn值均大于1.94，属于噪声主导分量。对PD主导分量采取SG滤波处理，对噪声主导分量采取改进小波阈值降噪处理，再进行重构得到去噪后的PD信号。此外，本文选取AVMD算法[3]、CEEMD-EEMD[17]算法、S-SVD[25]算法与所提方法去噪效果进行对比，结果如图10所示。

图10 仿真PD信号去噪结果

由图10(a)可知，含噪PD信号在经AVMD处理后还存在大量白噪声，去噪效果不理想；由图10(b)可知，CEEMD-EEMD算法虽能改善模态混叠现象，但无法完全消除；图10(c)中S-SVD的去噪效果要明显好于前两者，但第一个PD信号出现了放电起始点偏移的现象，影响后续的处理(定位、模式识别等)；由图10(d)可知，经过本文方法去噪后的波形与原始PD信号基本一致，能有效去除高斯白噪声与周期窄带干扰。

为了研究在不同程度白噪声下本文方法的去噪效果，在图8(a)的纯净PD信号中加入不同程度的白噪声，使其信噪比分别为-3 dB、0 dB、3 dB，再叠加相同程度的窄带干扰，利用2.2节中提到的指标对不同去噪方法进行评价，结果如表3所示。可以看出，本文提出的方法在相同条件下的去噪评价指标要优于其他3种算法。此外，由于本文方法整体结构较为复杂，在仿真时调用了大量外部函数，使得算法的运行时长较长，其中数次仿真时长达5 s，在后续对Sdr_SampEn值的计算中可对算法参数进行优化，提高时效性。

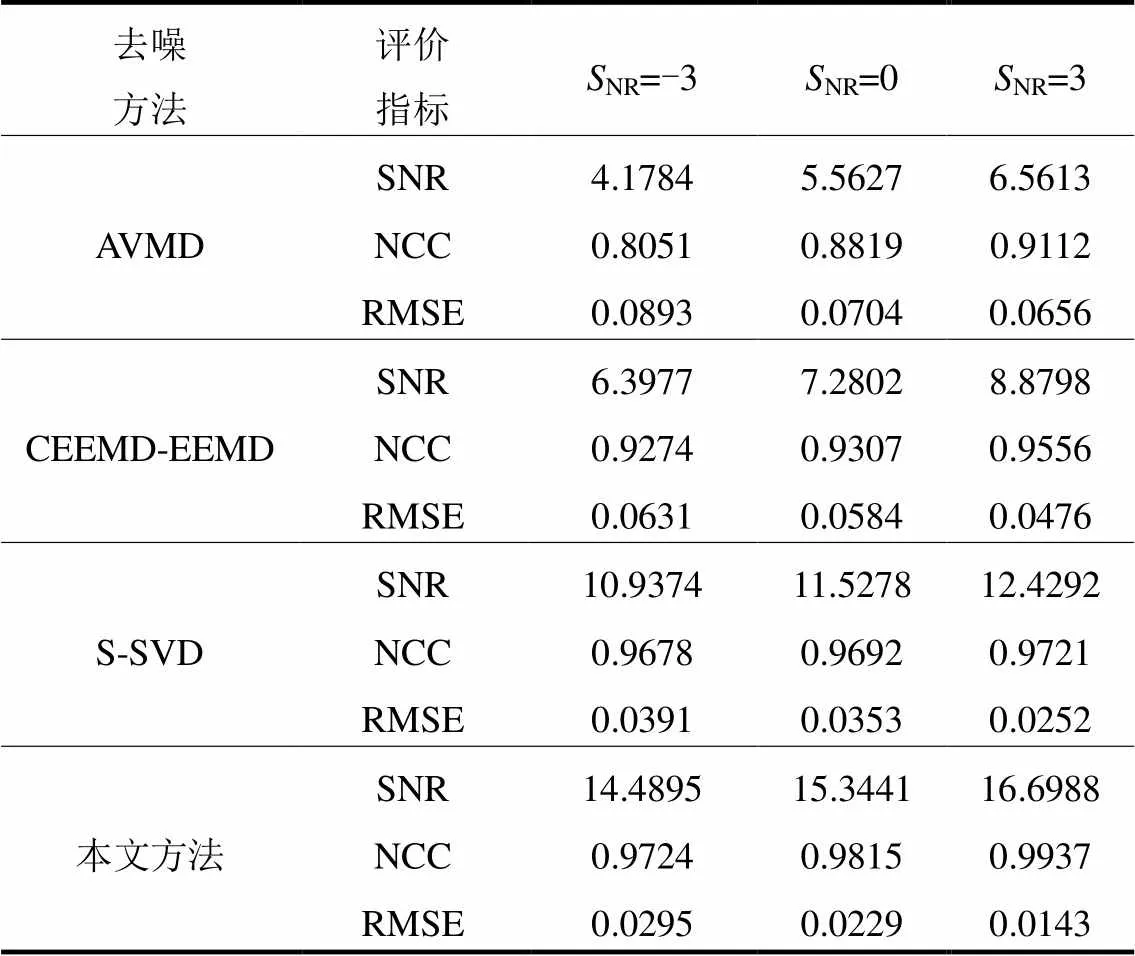
表3 不同信噪比下仿真PD信号去噪效果对比

4  实测信号分析

为进一步验证本文所提去噪方法的有效性，在实验室搭建了如图11所示的局部放电测试平台对10 kV电缆的实测PD信号进行处理。将采样频率为50 MHz的高频电流传感器(High Frequency Current Transformer, HFCT)套在锤击电缆处的接地线上，通过示波器和PC得到局部放电的脉冲波形，如图12所示。

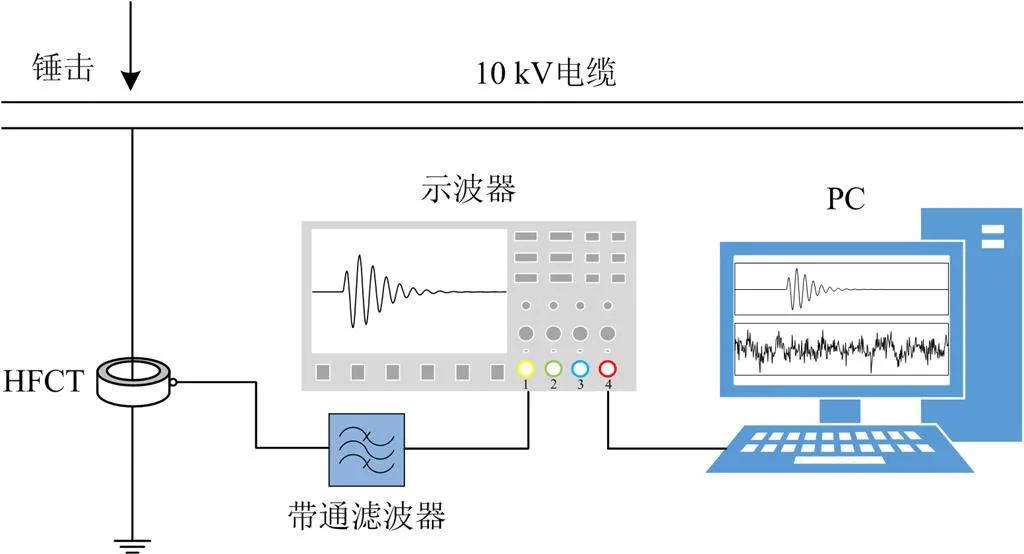
图11 局部放电测试平台

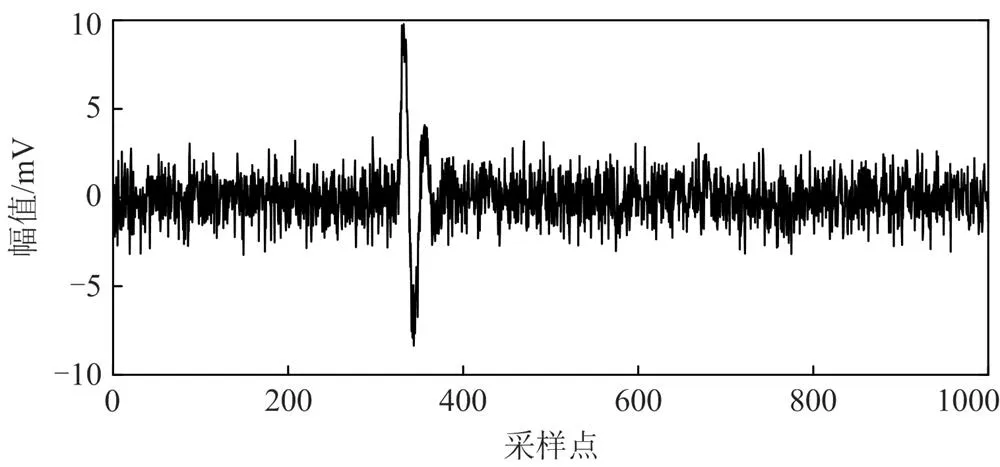
图12 实测PD信号

由于实验室测得的PD信号信噪比较高，因此在原始PD信号上人为添加幅值和频率分别为0.5 mV、1 mV、1.5 mV和0.8 MHz、1 MHz、2 MHz的窄带干扰，得到信噪比较低的含噪信号，如图13所示。

图13 叠加窄带干扰的PD信号

由图13可知，原始PD信号已完全被噪声淹没，无法辨别，且与图8(b)的含噪PD信号相类似，因此阈值的选取也相同。本文方法与其他3种去噪方法对实测PD信号进行去噪处理，结果如图14所示。

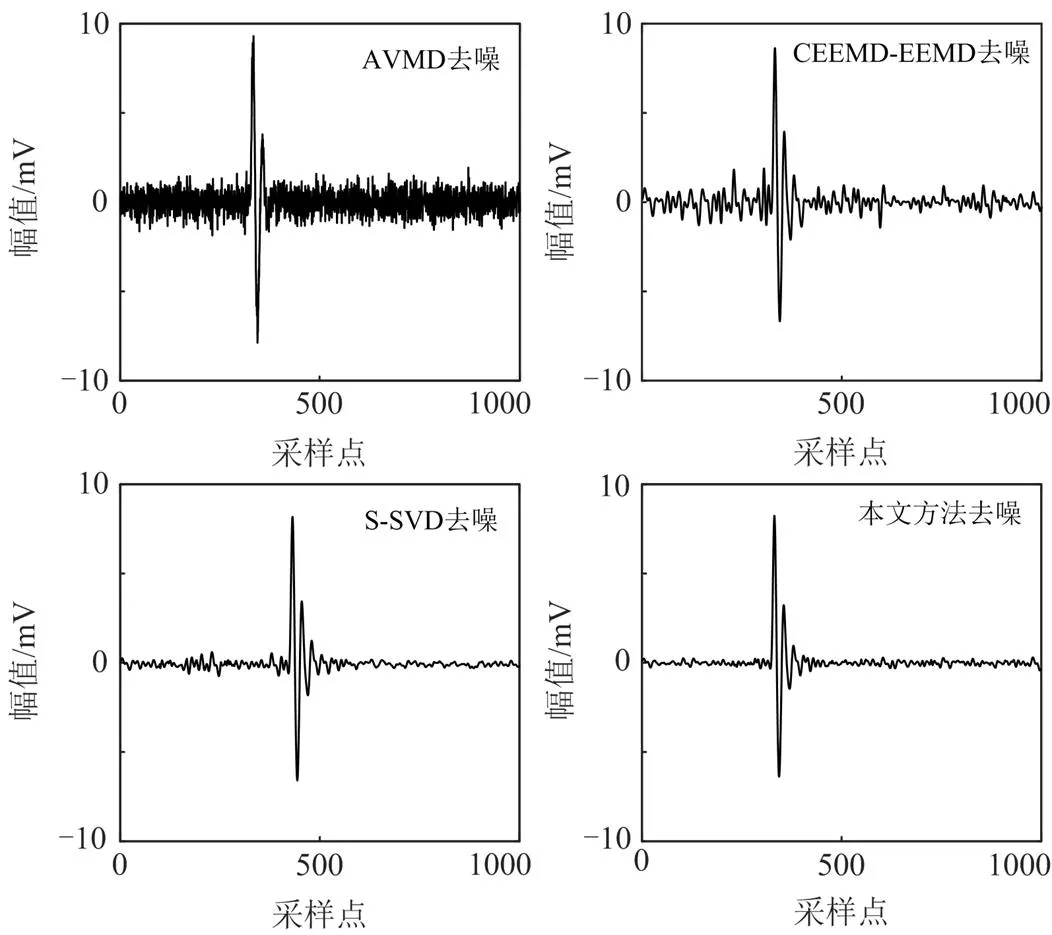
图14 实测PD信号去噪结果

由图14可知，经AVMD算法处理后的波形还有大量底噪；CEEMD-EEMD算法无法将白噪声和周期窄带干扰彻底去除，影响了PD信号的辨识；S-SVD去噪后，脉冲的起始点发生变化，影响后续的一系列工作。本文去噪方法的效果要明显优于上述3种方法，能有效抑制实测信号的噪声。分别计算4种去噪方法的NRR如表4所示，可以看出本文去噪方法的NRR最大，即对实测信号的去噪程度最大。

表4实测PD信号去噪效果对比

Table 4 De-noised results evaluation of lab-measured PD signal

5  结论

本文提出了一种基于S_VMD与Sdr_SampEn的局部放电信号去噪方法，通过对仿真与实测信号的分析，验证了本文去噪方法的效果，得出以下结论：

1) 本文去噪方法能有效抑制PD信号中的白噪声与周期窄带干扰，且去噪效果优于AVMD、CEEMD-EEMD和S-SVD算法。

2) VMD算法经Spearman相关系数优化获得最优参数后，能够对含噪信号完全分解。

3) 噪声主导分量中也含有部分PD信息，不可直接将其剔除，改进小波阈值算法能最大程度保留其中有用的PD信息。

4) 该方法通过求取各个IMF的Sdr_SampEn值，能准确辨别IMF的类别。

[1] 罗俊华, 杨黎明, 史济康, 等. 电力电缆及试验技术回顾[J]. 高电压技术, 2004, 30(增刊1): 81-82, 98.

LUO Junhua, YANG Liming, SHI Jikang, et al. Review of power cable and test technology[J]. High Voltage Engineering, 2004, 30(S1): 81-82, 98.

[2] 陶玉宁, 陈皇熹, 赵国伟, 等. 10 kV电缆中间接头典型施工缺陷的电场及局放特性研究[J]. 电力工程技术, 2021, 40(5): 114-120.

TAO Yuning, CHEN Huangxi, ZHAO Guowei, et al. Electric field and local discharge characteristics of typical construction defects of 10 kV cable intermediate joint[J]. Jiangsu Electrical Engineering, 2021, 40(5): 114-120.

[3] 吴童, 孙抗, 师文文. 基于AVMD-自适应小波包法的电缆局部放电去噪研究[J]. 电力系统保护与控制, 2020, 48(14): 95-103.

WU Tong, SUN Kang, SHI Wenwen. Research on cable partial discharge denoising based on an AVMD-adaptive wavelet packet method[J]. Power System Protection and Control, 2020, 48(14): 95-103.

[4] ABDEL-GALIL T K, El-HAG A H, GAOUDA A M, et al. De-noising of partial discharge signal using eigen- decomposition technique[J]. IEEE Transactions on Dielectrics & Electrical Insulation, 2008, 15(6): 1657-1662.

[5] 陶顺, 郭傲, 刘云博, 等. 基于矩阵束和奇异值分解的间谐波检测算法[J]. 电力系统保护与控制, 2021, 49(2): 57-64.

TAO Shun, GUO Ao, LIU Yunbo, et al. Interharmonic detection algorithm based on a matrix pencil and singular value decomposition[J]. Power System Protection and Control, 2021, 49(2): 57-64.

[6] 饶显杰, 周凯, 汪先进, 等. 基于改进SVD算法的局部放电窄带干扰抑制方法[J]. 高电压技术, 2021, 47(2): 705-713.

RAO Xianjie, ZHOU Kai, WANG Xianjin, et al. Suppression of narrow-band noise of partial discharge based on improved SVD algorithm[J]. High Voltage Engineering, 2021, 47(2): 705-713.

[7] 徐永干, 姜杰, 唐昆明, 等. 基于Hankel矩阵和奇异值分解的局部放电窄带干扰抑制方法[J]. 电网技术, 2020, 44(7): 2762-2769.

XU Yonggan, JIANG Jie, TANG Kunming, et al. A method of suppressing narrow-band interference in partial discharge based on Hankel matrix and singular value decomposition[J]. Power System Technology, 2020, 44(7): 2762-2769.

[8] 杨韬, 罗萍萍, 龚锦霞, 等. 基于改进无迹卡尔曼滤波的短线路同杆并架双回线参数辨识[J]. 电力系统保护与控制, 2021, 49(5): 36-45.

YANG Tao, LUO Pingping, GONG Jinxia, et al. Parameter identification of short parallel double-lines based on a modified unscented Kalman filter[J]. Power System Protection and Control, 2021, 49(5): 36-45.

[9] 赵彤, 梁家碧, 夏天翔, 等. 基于LMS自适应滤波算法的电力变压器有源降噪系统[J]. 高电压技术, 2016, 42(7): 2299-2307.

ZHAO Tong, LIANG Jiabi, XIA Tianxiang, et al. Active noise control system based on LMS adaptive filter algorithm for transformer power noise reduction[J]. High Voltage Engineering, 2016, 42(7): 2299-2307.

[10] LI Zhenxing, WAN Jialin, WANG Pengfei, et al. A novel fault section locating method based on distance matching degree in distribution network[J]. Protection and Control of Modern Power Systems, 2021, 6(2): 253-263.

[11] 唐炬, 樊雷, 卓然, 等. 用最优谐波小波包变换抑制局部放电混频随机窄带干扰[J]. 中国电机工程学报, 2013, 33(31): 193-201, 24.

TANG Ju, FAN Lei, ZHUO Ran, et al. Suppression of the random narrow-band noise with mixed frequencies in partial discharge with the optimal harmonic wavelet packet transform[J]. Proceedings of the CSEE, 2013, 33(31): 193-201, 24.

[12] 米翰宁, 王昕, 任广振, 等. 自适应小波阈值去噪算法用于局部放电白噪声去噪[J]. 高压电器，2021, 57(6): 94-101.

MI Hanning, WANG Xin, REN Guangzhen, et al. De-noising for white noise in partial discharge signals by adaptive wavelet threshold estimation[J]. High Voltage Apparatus, 2021, 57(6): 94-101.

[13] 王永强, 谢军, 律方成. 基于改进量子粒子群优化稀疏分解的局放信号去噪方法[J]. 电工技术学报, 2015, 30(12): 320-329.

WANG Yongqiang, XIE Jun, LÜ Fangcheng. PD signal denoising method based on improved quantum-behaved particle swarm optimization sparse decomposition[J]. Transactions of the China Electrotechnical Society, 2015, 30(12): 320-329.

[14] CHAN J C, MA H, SAHA T K, et al. Self-adaptive partial discharge signal de-noising based on ensemble empirical mode decomposition and automatic morphological thresholding[J]. IEEE Transactions on Dielectrics & Electrical Insulation, 2014, 21(1): 294-303.

[15] 孙博, 张建文, 潘磊落. 基于EMD的局部放电去噪方法的研究[J]. 绝缘材料, 2014, 47(3): 89-93.

SUN Bo, ZHANG Jianwen, PAN Leiluo.Study on de-noising method of partial discharge based EMD[J]. Insulating Materials, 2014, 47(3): 89-93.

[16] 胡爱军, 孙敬敬, 向玲. 经验模态分解中的模态混叠问题[J]. 振动·测试与诊断, 2011, 31(4): 429-434.

HU Aijun, SUN Jingjing, XIANG Ling. Mode mixing in empirical mode decomposition[J]. Vibration·Testing and Diagnosis, 2011, 31(4): 429-434.

[17] 彭炜文, 刘伟杰, 许家浩, 等. 一种基于相关系数的EEMD局部放电去噪方法[J]. 高压电器, 2021, 57(6): 203-215.

PENG Weiwen, LIU Weijie, XU Jiahao, et al. EEMD partial discharge de-noising method based on correlation coefficients[J]. High Voltage Apparatus, 2021, 57(6): 203-215.

[18] 高佳程, 田蕴卿, 朱永利, 等. 基于完全集合经验模态分解和排列熵的局部放电信号的小波包去噪方法[J]. 电力系统及其自动化学报, 2018, 30(3): 1-7.

GAO Jiacheng, TIAN Yunqing, ZHU Yongli, et al. Wavelet package denoising method for partial discharge signals based on CEEMD and PE[J]. Proceedings of the CSU- EPSA, 2018, 30(3): 1-7.

[19] 汤吉鸿, 朱军飞, 李勇, 等. 基于变分模态分解的电力系统泛频带振荡辨识方法[J]. 电力系统保护与控制, 2019, 47(2): 1-8.

TANG Jihong, ZHU Junfei, LI Yong, et al. VMD based mode identification for broad-band oscillation in power system[J]. Power System Protection and Control, 2019, 47(2): 1-8.

[20] LI G, YANG Z, YANG H. Noise reduction method of underwater acoustic signals based on uniform phase empirical mode decomposition, amplitude-aware permutation entropy, and Pearson correlation coefficient[J]. Entropy, 2018, 20(12).

[21] 孙抗, 张露, 王福忠. 基于变分模态分解和奇异值分解的局部放电信号去噪方法[J]. 河南理工大学学报(自然科学版), 2020, 39(6): 119-126.

SUN Kang, ZHANG Lu, WANG Fuzhong. Partial discharge signal denoising method based on variational mode decomposition and singular value decomposition[J]. Journal of Henan Polytechnic University (Natural Science), 2020, 39(6): 119-126.

[22] 王文波, 张晓东, 汪祥莉. 基于独立成分分析和经验模态分解的混沌信号降噪[J]. 物理学报, 2013, 62(5): 27-34.

WANG Wenbo, ZHANG Xiaodong, WANG Xiangli. Chaotic signal denoising method based on independent component analysis and empirical mode decomposition[J]. Acta Physica Sinica, 2013, 62(5): 27-34.

[23] PHAM T D, YAN H. Spatial-dependence recurrence sample entropy[J]. Physica A Statistical Mechanics & Its Applications, 2018, 494: 581-590.

[24] 王勇, 邓四二, 王恒迪. 基于SG滤波器和组合窗STFT的滚动轴承故障诊断方法[J]. 轴承, 2011(8): 43-46.

WANG Yong, DENG Si'er, WANG Hengdi. Fault diagnosis method for rolling bearings based on SG filter and STFT with combining window functions[J]. Bearing, 2011(8): 43-46.

[25] 刘宇舜, 周文俊, 李鹏飞, 等. 基于广义S变换模时频矩阵的局部放电特高频信号去噪方法[J]. 电工技术学报, 2017, 32(9): 211-220.

LIU Yushun, ZHOU Wenjun, LI Pengfei, et al. Partial discharge ultrahigh frequency signal denoising method based on generalized S-transform modular time-frequency matrix[J]. Transactions of the China Electrotechnical Society, 2017, 32(9): 211-220.

[26] 庞曦, 王晨晨, 孙伟翔. 基于多分辨VMD算法的大地电磁信号去噪效果研究[J]. 煤炭科学技术, 2021, 49(5): 227-233.

PANG Xi, WANG Chenchen, SUN Weixiang. Study on removing noise effect of magneto telluric signals based on multi-resolution VMD algorithm[J]. Coal Science and Technology, 2021, 49(5): 227-233.

[27] 张大海, 杨宇辰, 刘艳梅, 等. 基于EMD与Spearman相关系数的混合直流线路纵联保护方法[J]. 电力系统保护与控制, 2021, 49(9): 1-11.

ZHANG Dahai, YANG Yuchen, LIU Yanmei, et al. Hybrid HVDC line pilot protection method based on EMD and Spearman correlation coefficient[J]. Power System Protection and Control, 2021, 49(9): 1-11.

[28] 佘昌佳, 梅飞, 叶昱媛, 等. 基于优化VMD与噪声估计的间隔阈值局部放电去噪方法[J]. 高压电器, 2020, 56(3): 141-149.

SHE Changjia, MEI Fei, YE Yuyuan, et al. Partial discharge signal denoising method based on optimized VMD and noise estimation for interval threshold[J]. High Voltage Apparatus, 2020, 56(3): 141-149.

[29] 李天云, 高磊, 聂永辉, 等. 基于经验模式分解处理局部放电数据的自适应直接阈值算法[J]. 中国电机工程学报, 2006, 26(15): 29-34.

LI Tianyun, GAO Lei, NIE Yonghui, et al. A new adaptive direct-threshold algorithm to partial discharge data processing based on empirical mode decomposition[J]. Proceedings of the CSEE, 2006, 26(15): 29-34.

[30] 张悦, 陈孝信, 钱勇, 等. XLPE电缆交叉互联系统中局放脉冲时域特征仿真研究[J]. 高压电器, 2021, 57(7): 112-118.

ZHANG Yue, CHEN Xiaoxin, QIAN Yong, et al. Simulation study on time domain feature of partial discharge pulse in XLPE cable cross-bonding system[J]. High Voltage Apparatus, 2021, 57(7): 112-118.

A denoising method for a partial discharge signal based on S_VMD and Sdr_SampEn

MA Xinghe1, 2, KONG Weidong1, LI Ziqiang3, WANG Wansong4, BAO Jingwen5

(1. School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo 454000, China;2. Henan Key Laboratory of Intelligent Detection and Control of Coal Mine Equipment, Jiaozuo 454000, China;3. XJ Electric Co., Ltd., Xuchang 461000, China; 4. Nanjing DAQO Electric Co., Ltd., Nanjing 211106, China;5. Henan Pinggao Electric Co., Ltd., Pingdingshan 467000, China)

XLPE cables, an important tool for power transmission in the carbon peaking and carbon neutrality goals, suffer from a decline in insulation performance after a number of years. Partial discharge (PD) detection has been widely used as an important means to evaluate the insulation status of XLPE cables. To solve the problem of various types of noise in PD signals,a PD signal denoising method based on Spearman variational mode decomposition (S_VMD) and spatial dependence recurrence sample entropy (Sdr_SampEn) is proposed. First, the signal is decomposed intooptimal intrinsic mode functions (IMF) through S_VMD. Secondly, the Sdr_SampEn value of each IMF is calculated to determine whether the IMF is the noised-dominated IMF or the PD-dominated IMF. After classification, the IMF will be denoised by improved wavelet threshold denoising and Savitzky-Golay (SG) filter denoising. Finally, the processed IMF will reconstructed, and the noise-reduced signal is acquired. This method is used to denoise the simulated and lab-measured PD signals, and it is further compared with many denoising algorithms such as adaptive variational mode decomposition (AVMD), etc. The results prove that the proposed method can effectively remove various types of noise, and thus shows engineering value.

XLPE cable; PD; Spearman correlation coefficient; VMD; Sdr_SampEn

10.19783/j.cnki.pspc.211572

2021-11-22；

2022-02-25

马星河(1979—)，男，博士，副教授，研究方向为电气设备状态监测；E-mail: maxinghe@hpu.edu.cn

孔卫东(1998—)，男，通信作者，硕士研究生，研究方向为电力系统优化与控制。E-mail: kongweidong101@ 126.com

国家自然科学基金项目资助(U1404522)；河南省科技攻关项目资助(182102310936)

This work is supported by the National Natural Science Foundation of China (No. U1404522).

(编辑 姜新丽)