人体关键点升维算法及其在游戏交互中的应用

李长鑫，黄海于

（西南交通大学 计算机与人工智能学院，成都 610031）

0 引 言

随着信息技术的不断进步，人机交互技术在计算机领域的作用显得越发重要。目前，对于符合人类交流习惯的“自然”智能人机交互技术研究已经引起学界高度关注，大量科研人员投身到人体姿态、手势、肢体动作、人脸表情、语音等方式的人机交互研究中。人机交互技术正在逐步从以计算机为中心转变为以人为中心。

在游戏娱乐方面，使用键盘、鼠标操作的游戏已然无法满足用户体验的多样化需求。因此，为了提高用户体验，VR游戏应运而生。传统的VR游戏通常需要笨重的辅助设备，在加大了游戏玩家负担的同时，也增加了成本。为了解决上述问题，基于计算机视觉技术的体感游戏已日益受到人们的关注重视。该交互方式通常依赖于人体关键检测算法，通过算法得到人体关键点坐标信息，控制游戏内玩家角色的运动，从而实现与游戏内容的交互。

针对人体关键点检测算法只能对单一RGB图像进行2D关键点检测的问题，本文提出了一种将像素坐标系下2D人体关键点坐标升维至世界坐标系下3D人体关键点坐标的方法，实现了仅通过2个RGB摄像头，便可实时获取游戏玩家在世界坐标系下的3D关键点信息，从而控制游戏中玩家角色的骨骼动画，以此达到控制游戏中玩家角色位置移动、姿态变化、操作触发等一系列交互操作的目的。

1 相关研究

在基于人体关键点检测的游戏交互应用中，如何实现对人体关键点在现实空间中的三维定位、尤其是深度信息的获取，即已成为研究的重点和难点。按照定位原理的不同，这类游戏的交互主要采用结构光、TOF和双目立体视觉等交互方式。

1.1 基于结构光的游戏交互

结构光的交互方法是通过投影仪，将IR红外光投射到被测物体表面，用摄像机拍摄被测物体采集结构光图像。若已知摄像机坐标系与投影仪坐标系之间的相对位置关系，则可求解出被测物体上的光条在摄像机坐标系或者投影仪坐标系中的具体坐标。该方法的精度范围为mm到cm之间，由于需要投影和摄像机等辅助设备，该类产品价格普遍都比较贵，通常在几千到几十万不等，代表产品有Kinect1.0、RealSense。此外，应用该类方法的产品还存在受光照影响较大、响应较慢的缺点。

1.2 基于TOF的游戏交互

时间飞行法（Time of Flight，TOF）通过发射连续的光脉冲到被观测物体上，并接收从物体反射回来的光脉冲。通过探测光脉冲的飞行时间，计算被测物体与相机间的距离。该方法的精度范围为μm到cm之间，需要发射器和检测器作为辅助设备，存在价格昂贵（高精度的设备价格可达上百万）、受强光影响大的缺点。代表性产品有Kinect2.0。

1.3 基于双目立体视觉的游戏交互

双目立体视觉是将2个完全相同的摄像头平行放置，同步采集前方图像。由于2个摄像头位置不同，对同一目标点所采集的图像必然存在一定的像素差（视差），由视差可计算出目标点到双目摄像头的距离，该类方法的精度通常在cm级。考虑到传统的双目立体视觉方法需要借助于立体匹配，即使得该类方法存在算法复杂度高、受光照影响大、精度不高的缺点。代表性产品有Leap Motion等。由于此类方法的效果并不理想，因此目前没有典型的应用场景，大多只用于学术研究。

2 本文方法

本文方法是对传统基于双目立体视觉方法的改进。本方法依托于2D人体关键点检测算法，直接对2D人体关键点检测结果升维，得到该关键点在世界坐标系下的三维坐标。与传统的基于双目立体视觉方法相比，该方法不需要立体匹配算法，只依赖于深度学习算法对人体关键点的检测结果，受光照等环境影响小，故可以应用于复杂场景。并且，也同样都不需要建立视差图，因此大大减小了算法的时间复杂度，在保证结果精度的同时，极大提升了算法的效率，更适用于游戏的实时应用场景。此外，直接对2D关键点进行升维，也在一定程度上避免了误差的累积。

2.1 坐标系与坐标转换

在计算机视觉领域主要有4种坐标系，分别是：世界坐标系（X，Y，Z）、相机坐标系（X，Y，Z）、图像坐标系，( )、像素坐标系（，）。

从世界坐标系到像素坐标系之间的转换关系可表示为：

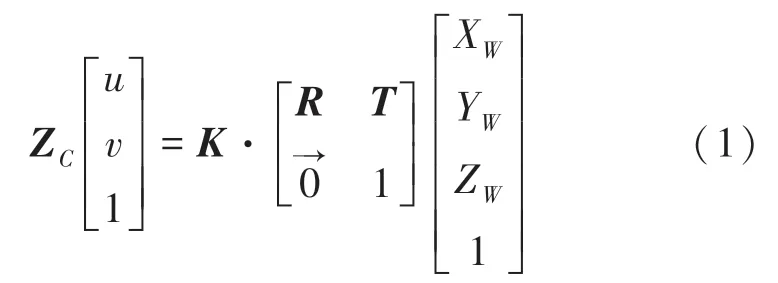
其中，为相机的内参矩阵；为旋转矩阵；为偏移向量（、又称作相机的外参）；Z表示尺度因子。

由此可见，如果知道相机的内参矩阵、旋转矩阵和偏移向量，就可以实现从像素坐标系到世界坐标系的转化。相机的内参矩阵和外参均可以通过相机标定得到。

2.2 相机外参标定

内参矩阵是相机的固有属性，可通过张正友标定来获得，通常情况下不会改变，因此只需要标定一次。

外参表示的是相机在世界坐标系中的位置和姿态，需要将相机悬挂好后，再进行标定，而且只要移动一次相机，就必须重新对外参进行标定。

本文以地面作为标定的基准面进行相机外参标定，建立如图1所示的世界坐标系。因地面上所有点的坐标均为0，则只需要知道相机相对于地面的关系，就可求出相机外参。由于确定一个平面至少需要3个点，因此只需要指定4个地面上的参考点，再通过相机的内参矩阵代入式（1）即可求得旋转矩阵和偏移向量。

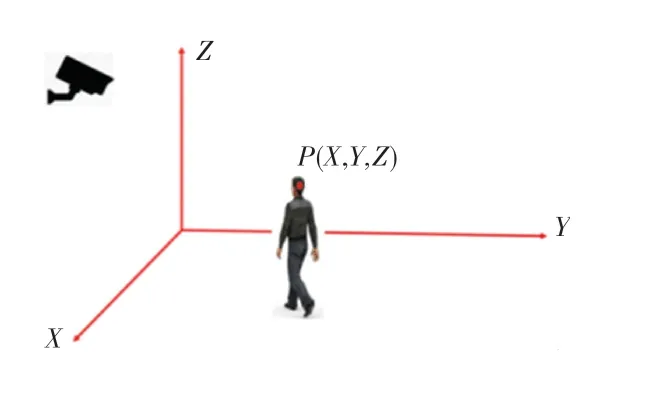
图1 指定的世界坐标系Fig.1 Specified world coordinate system

2.3 升维原理

为了实现通过像素坐标系（，）反求该空间点所对应的世界坐标系（X，Y，Z），可将式（1）变形得到式（2）：

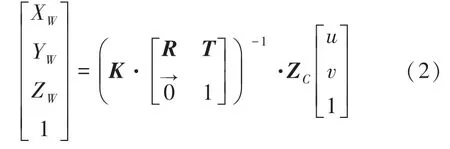
通过分析式（2）可知，内参矩阵、旋转矩阵、偏移向量均已通过相机标定得到，只有尺度因子Z未知。

为求得尺度因子Z，还需要借助世界坐标系到相机坐标系的转换关系，其数学公式见如下：

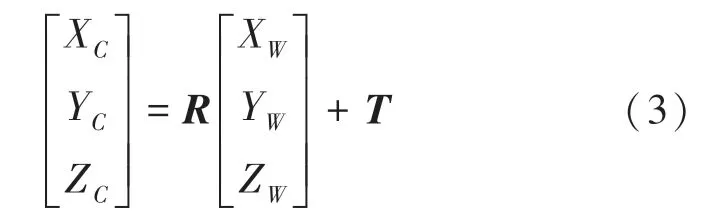
在已知Z的情况下，可求出Z。而当被测点在地面上时，即Z＝0，通过式（3）即可求得尺度因子Z，再将尺度因子Z代入式（2）就可求得（X，Y，Z＝0）。

综上所述，在已知Z＝0时，可以实现从像素坐标（，）到世界坐标（X，Y，Z）的转换。

在实际应用中，并不能保证被测点一定是在地面上，即被测点的Z≠0，Z的值通常未知，该情况需要采用双镜头对该点同时检测的方式求得，原理如图2所示。

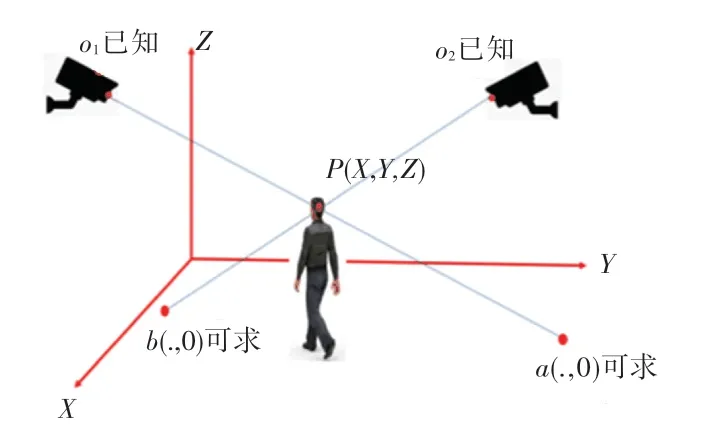
图2 双目定位原理Fig.2 Binocular positioning principle

设待定位的空间点为，摄像头1、2的相机坐标系原点分别为为、；通过摄像头1、2的投影点分别为、。此时点、的世界坐标的坐标Z均为0，投影点的世界坐标（X，Y，Z＝0）与投影点的世界坐标（X，Y，Z＝0）均可通过式（2）求出，摄像头的世界坐标（X，Y，Z）和摄像头的世界坐标（X，Y，Z）可通过式（3）求得。通过与可确定空间直线，通过与可确定空间直线，与的交点即为的世界坐标。

2.4 解空间直线方程的近似方法

在图2中，由于和是2条空间直线，当两直线平行或者不共面时，则方程无解，而在本文算法应用场景中，不会出现两直线平行的情况。由于2D关键点检测算法精度的影响，两摄像头对空间中同一点的检测总会存在偏差，因此造成两直线不共面、而方程无解的情况。为了解决该问题，本文提出以下方法求解空间直线方程。

解空间直线方程示意如图3所示，在已知、、、四个空间点的情况下，求与的交点，过点作平行四边形，根据相似三角形法则，可知S／S＝AO／AB。而三角形与三角形的面积可以通过空间向量的叉积公式求得，即可求出与的比例关系，最终求得交点的三维坐标。

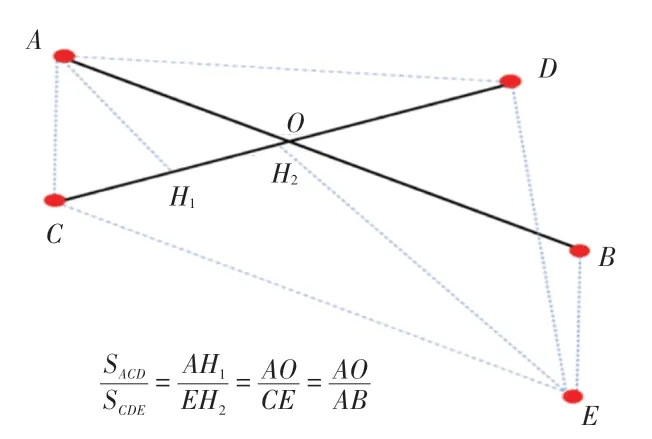
图3 解空间直线方程示意图Fig.3 Schematic diagram of solving the equation of a straight line in the space

在图2中，已知摄像头的世界坐标（X，Y，Z）和的世界坐标（X，Y，Z），投影点的世界坐标（X，Y，Z＝0）与的世界坐标（X，Y，Z＝0）。根据上述原理，空间点的世界坐标（X，Y，Z）可通过式（4）求出：

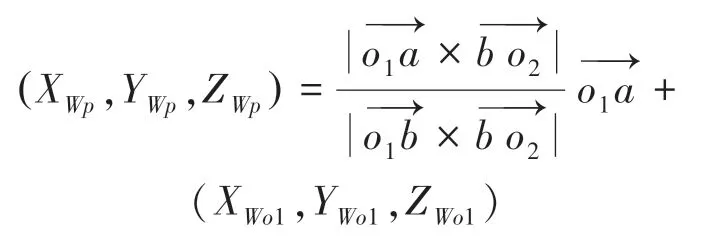
其中：

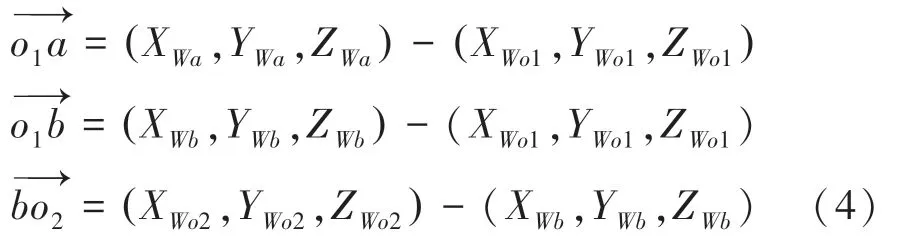
该方法在有解情况下与常规方法结果相同，在两直线不共面的情况下，也可以得到一个近似解，而且易于编程，满足应用需求。但是，解的精确度与两摄像头的摆放位置相关，当两摄像头的光轴越接近于平行，解的误差越大。因此实际应用时，悬挂摄像头时应使两光轴有一定角度，并经过多次测试选择解的精度最高的悬挂方式。

2.5 算法流程及复杂度分析

该升维算法可划分为相机标定、升维结果计算两个阶段。对此拟做阐释分述如下。

（1）相机标定阶段。是整个算法流程的准备阶段，仅需进行一次，因此该阶段所耗费的时间可以忽略不计，误差主要来自于张正友标定方法本身的误差和测量误差。该阶段的目的是为获取两摄像头的内参矩阵、旋转矩阵和偏移向量，并由此计算出两摄像头原点的世界坐标。计算世界坐标的伪代码。

该阶段为整个算法流程的核心，所耗费的时间主要取决于2D人体关键点检测算法，其余部分时间复杂度均为常数。误差主要来源于2D人体关键点检测算法的误差以及求解空间直线方程时产生的误差。

3 实验结果与分析

3.1 定量结果分析

为定量测试升维算法的准确度，对该升维算法在250 cm*250 cm的空间内进行了测量。测量详情见图4。图4中，在一把椅子上标注4个检测点，不断移动椅子的位置，通过升维算法对椅子的检测点进行定位，并比较预测位置与实际位置的误差。

图4 升维算法定量测试Fig.4 Quantitative test of dimension-ascending algorithm

共进行了9组实验，具体结果见表1。表1中，单位均为cm，且保留整数。分析表1中数据，可得出结论：在本文实验条件下，该升维算法的平均绝对误差为2.105 cm。

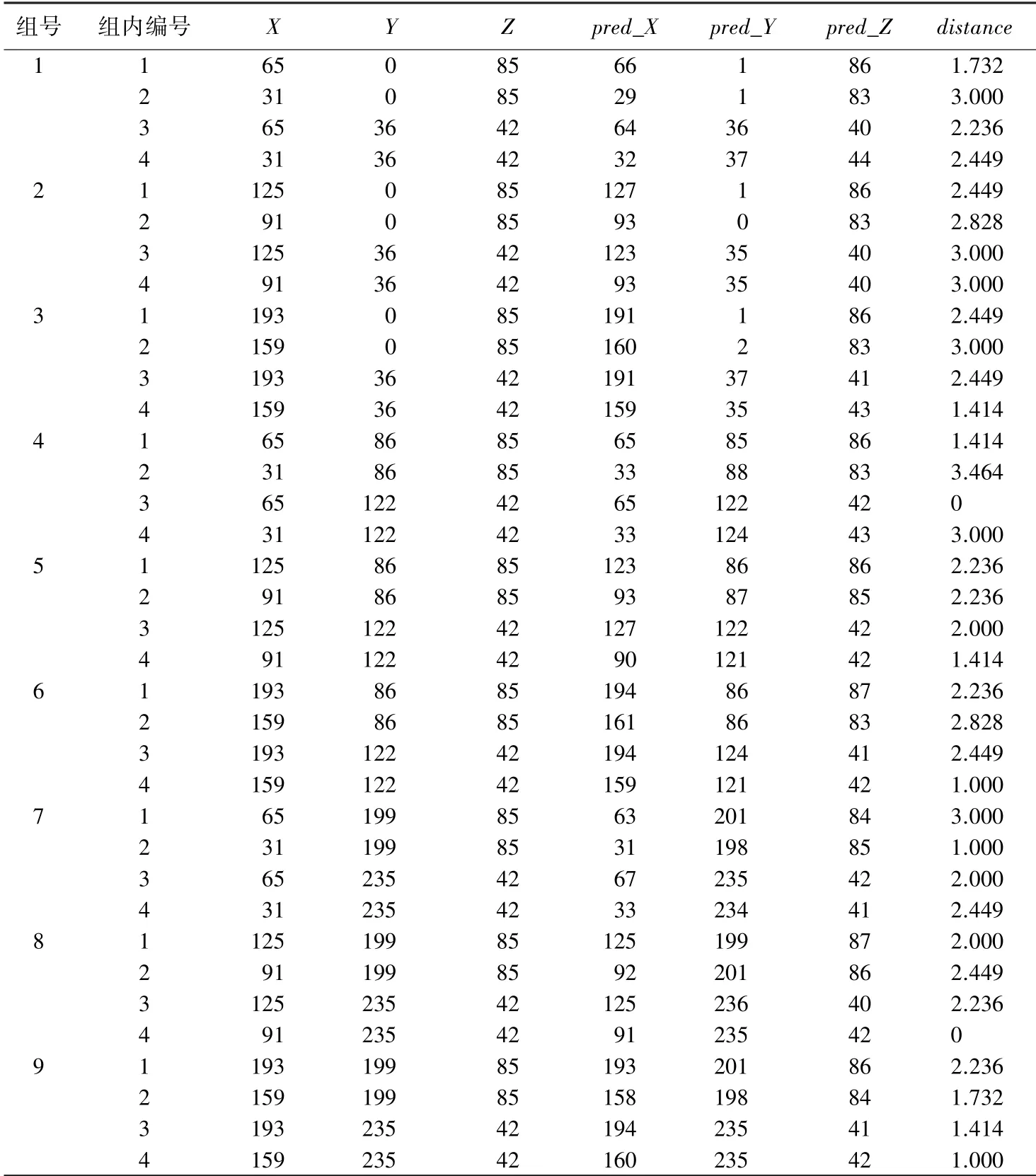
表1 升维算法定量测试结果Tab.1 Quantitative test results of dimension-ascending algorithm cm

3.2 可视化结果分析

本文将作为2D人体关键点检测器，并定义了一系列的关键点，见表2。同时，又将的检测结果进行升维，得到每个关键点的三维世界坐标。

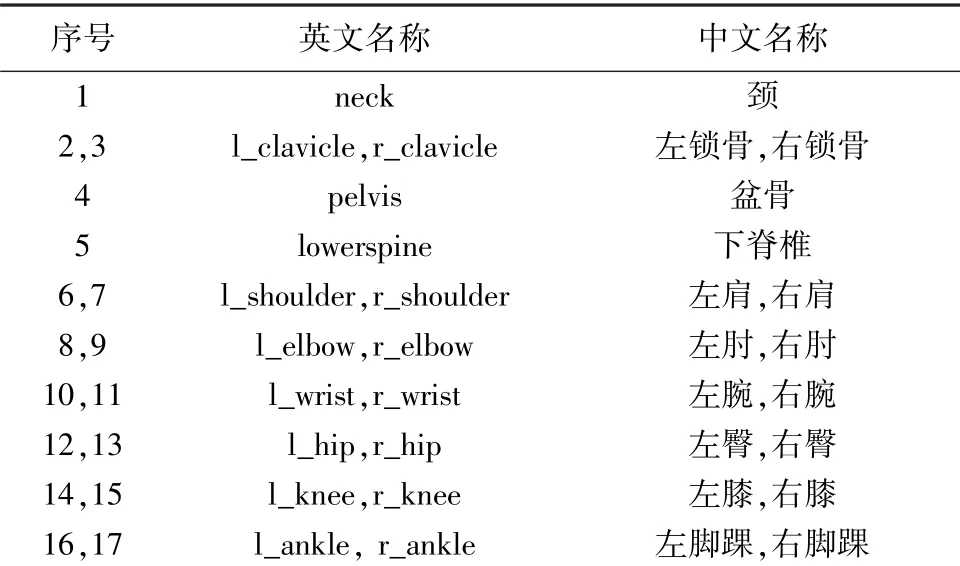
表2 关键点定义Tab.2 Key points definition

本文通过2个RGB摄像头先进行2D人体关键点检测、再进行升维的方法，能够得到较好的效果，并达到实际项目应用要求，测试效果如图5所示。

图5 升维效果Fig.5 Dimension-ascending effect

3.3 交互测试结果分析

为了达到游戏玩家通过动作变化来控制第三人称游戏中玩家角色模型运动、从而实现人机交互的目的，本文将上述通过关键点升维得到的3D人体关键点数据，作为游戏交互信息进行了测试。本地客户端将3D关键点数据以一定格式发送给游戏运行平台。游戏运行平台得到人体关键点的3D坐标数据后，通过内插或运动学分析等处理方法，来完成对游戏内玩家模型的控制。交互效果如图6所示。文中经交互测试可看出，对于通过升维算法得到的3D关键点数据，能够有效地用于游戏交互，并得到较好的效果。

图6 交互结果Fig.6 Interaction results

4 结束语

针对RGB图片只能进行2D关键点检测问题，提出了一种通过2个普通RGB摄像头对同一关键点检测，再根据两摄像头的空间关系对像素坐标系下的2D坐标进行升维，得到其在世界坐标系下3D坐标的升维方法。经过测试，通过该方法得到的3D坐标有较高的准确度，并且可以用于对第三人称游戏玩家角色的交互。在保证玩家游戏体验的同时，降低了体感类游戏的硬件成本。此外，该升维方法有较好的拓展性，可用于各种场景。