基于能量距离法的多维分类变量的分布差异检验
2022-09-27彭东海张留伟
彭东海,张留伟
(1.中山职业技术学院数学教研室,广东 中山 528404;2.中山大学测绘学院,广东 珠海 519082)
0 引言
分类数据又称定性数据,它是反映对象的属性特征,是非量化的数据。例如,社会调查数据中的性别、职业、学历、婚姻状况等;医学研究数据中病人的血型、吸烟与否、采取的治疗方案的类别、检测结果的阳性与阴性等。可见,分类数据是我们实际生活中广泛存在的一类数据类型,因而比较两组分类数据的分布差异也就成了我们经常遇到的问题。例如,比较两个不同行业从业人员的学历结构差异,或比较不同性别职业分布差异等。这类问题概括来说,就是要比较两个独立的分类变量的分布差异,用数学语言表述如下:
假设X与Y是两个独立的离散型随机变量,概率分布列分别为:
P(X=ai)=pi,i=1,2,…,r,
与
P(Y=ai)=qi,i=1,2,…,r.
其中,pi≥0,qi≥0, ∑ipi=1,∑iqi=1.它们对应的分布函数分别为F与G,考虑检验问题:
H0∶F=G
(1)
即
H0∶pi=qi,∀i=1,2,…,r.
(2)
假设X1,X2,…,Xm是来自X的简单随机样本,Y1,Y2,…,Yn是来自Y的简单随机样本。对各样本进行汇总后,可得频数分布如表1、2:

表1 X的样本频数分布表
检验问题(1)的经典方法为卡方检验,卡方检验将X的样本X1,X2,…,Xm与Y的样本Y1,Y2,…,Yn进行合并,并对每个样本添加标签,标注它是来自X的样本还是来自Y的样本。因此,检验X与Y是否同分布等价于检验标签变量与分类值是否相互独立,从而,我们可将表1的X的样本频数分布表与表2的Y的样本频数分布表合并成一个新的如表3所示的列联表:

表2 Y的样本频数分布表

表3 X与Y的样本的频数列联表
基于此表,可构造卡方检验统计量:

众所周知,卡方检验仅适用于大样本情形,它要求列联表中小于5的理论次数不能多于20%.因此,当X与Y取值的类别比较多,而样本量又不够大时,容易出现列联表中很多单元格频数小于5,甚至为0.此时,如果我们仍采用卡方检验来检验两个分布的差异,则可能会得到错误的结论。在此情形下,可参考文献[1]关于卡方检验的一些传统的修正方法。
能量距离 (Energy distance,ED)的概念由Székely 与Rizzo 在文献 [2]中提出,它是由两个独立随机向量的特征函数之差的模构造的,在选取一个特殊的权重函数进行积分之后,它可以表示成距离函数的期望形式。ED等于0当且仅当两个分布相同,因此,ED是度量两个独立随机向量分布差异的一个很好的测度。而样本的ED只涉及两点之间的距离的计算,它可以用来检验两个独立样本是否同分布,它检验的对象可以是任意有限维数的随机向量,只须满足有限一阶矩的条件即可,并且检验方法具有一致性。Székely 与Rizzo 在文献[3~8]中分别展示了将ED用于处理诸如独立样本同分检验、单样本分布检验、聚类分析等一系列经典统计问题的结果。这些研究结果表明,相比传统的方法,ED方法计算简便、适用于更广泛分布类型的数据,且能处理多变量情况。近年来,ED方法引起了国内不少学者的关注。文献[9]讨论了基于ED推广的Ward聚类算法研究,文献[10]对ED做了几点补充讨论,文献[11]则将ED用于二维列联表的独立性检验问题中,得到了一个比传统卡方检验计算更简便、在小样本情形下具有更功效的检验统计量。
本文受文献[1]启发,基于独立变量的ED概念,通过引入虚拟向量的方式,给出了两个分类变量的ED的总体形式与样本估计,基于该样本估计,我们得到了一种新的检验方法,并采用置换程序计算该方法的检验p值。数值模拟显示,相比传统的卡方检验法,我们的方法不受列联表中单元格的频数影响,因此,大部分时候具有更高的功效。最后,我们将方法应用于一份涉及两个多维分类向量的分布差异检验的数据中。
1 能量距离(ED)方法简介
我们先回顾一下文献[1]提出的两个独立的随机变量的能量距离(ED)的定义及主要结果。
定义1[1]设X、Y为取值于d的两个独立的随机向量,并且E|X|+E|Y|<∞,则X与Y的能量距离(ED)定义为:
ε(X,Y)∶=2E|X-Y|-E|X-X′|-E|Y-Y′|
其中|.|表示欧氏距离,X′是与X独立同分布的随机变量,Y′是与Y独立同分布的随机变量。


假设X1,X2,…,Xm是来自X的简单随机样本,Y1,Y2,…,Yn是来自Y的简单随机样本,则ε(X,Y)的样本估计为

(7)
文献[1]证明了εm,n(X,Y)如下的大样本性质:

定理2[1]设X与Y为取值于d的两个独立的随机变量,X,Y分别有分布函数F,G,且E|X|+E|Y|<∞.则当X与Y的分布相同时,有

(8)

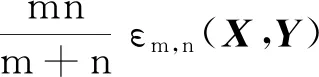
步骤1:由原始样本{X1,X2,…,Xm}和{Y1,Y2,…,Yn}计算检验统计量Tm,n;
步骤2:对联合样本{Z1,Z2,…,Zm,Zm+1,…,Zm+n}={X1,X2,…,Xm,Y1,Y2,…,Yn}随机地重新排列得
{Zπ(1),Zπ(2),…,Zπ(m),Zπ(m+1),…,Zπ(m+n)}

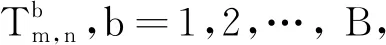

(9)
2 分类变量的能量距离
定义1中给出的能量距离的概念针对的两个随机向量X、Y要求为数值型变量,若X与Y为分类变量(向量),我们无法直接用(8)式给出的Tm,n统计量来检验X与Y的分布差异。为此,我们首先对X与Y构造相应的虚拟变量,将X与Y的分布差异检验问题等价地转换成对两个虚拟向量的分布差异的检验。具体地,记ei,i=1,2,…,r为r空间中第i个分量元素为1,其他位置元素均为0的单位向量,引入虚拟向量eX与eY如下:
eX=ei,若X=ai,i=1,2,…,r,
及
eY=ei,若Y=ai,i=1,2,…,r.
显然,P(eX=ei)=P(X=ai)=pi及P(eY=ei)=P(Y=ai)=qi,i=1,2,…,r.因此,检验X与Y是否同分布等价于检验eX与eY是否同分布。即我们将分类变量X与Y的分布差异检验问题等价地转换成了Rr空间中两个随机向量的eX与eY的分布差异的检验问题。此时,eX与eY的能量距离有表达式:
ε(eX,eY)=2E|eX-eY|-E|eX-eX′|-E|eY-eY′|
其中,eX′是与eX独立同分布的随机向量,eY′是与eY独立同分布的随机向量。ε(eX,eY)的样本估计相应为:
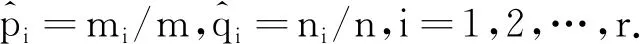
3 数值模拟
在这一节中,我们利用R软件通过几个简单的模拟实验来比较本文提出的方法与传统的卡方检验的表现。考虑以下6个例子:

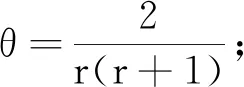
例3:X与Y独立,均以q,q2,…,qr-1, 1-(q+q2+…+qr-1) 的概率分别取a1,a2,…,ar,其中
q=1/2;


1-(q+q2+…+qr-1)的概率分别取a1,a2,…,ar,其中q=1/2;

显然,上面例子中,例1至例3为X与Y同分布的情形,而例4至例6为X与Y不同分类的情形。类别个数考虑r=3, 5, 10, 20, 40五种情况,设定显著性水平α=0.05,Tm,n通过499次置换计算p值,样本容量考虑:1)m=30,n=50; 2)m=50,n=80; 3)m=80,n=100; 4)m=100,n=100; 5)m=100,n=150五种情况。所有的模拟都通过1 000次重复试验来近似相应的第一类错误与功效。表4给出了各种情形下卡方检验与Tm,n的模拟结果。
从表4中我们可以看到,对于例1至例3,Tm,n在各种情形下都能将第一类错误很好地控制在名义水平0.05附近,而卡方检验在r=20与r=40的情形下,当样本量较小(如m=30,n=50与m=50,n=80)的时候,第一类错误远小于名义水平0.05.这是因为,当分类的类别个数较多,而样本量较小时,列联表中可能会出现很多单元格的期望频数小于5,从而导致卡方检验统计量近似卡方分布的效果不好,因此第一类错误不准确。很明显,在样本量增大的过程中,这种情况稍微得到了改善,卡方检验的第一类错误逐渐靠近名义水平。对于例4至例6,在类别个数r≤10,且样本量较大(如m=80,n=100及以上)时,大部分时候卡方检验的功效稍微高于Tm,n,但在样本量较小(如m=30,n=50)时,或类别个数较多(如r=40)时,卡方检验的功效均不如Tm,n.总的来说,我们的方法Tm,n在小样本或类别个数较多时相比卡方检验更有优势。

表4 6个例子在不同样本容量下卡方检验与Tm,n检验法的第一类错误与功效比较(α=0.05)
4 实例分析
本小节中,我们利用本文提出的方法来分析一份实际数据。数据来源于R软件的MASS包中的birthwt数据集,该数据集记录了1986年在马萨诸塞州斯普林菲尔德的Baystate医疗中心产妇与新生儿的信息,共189条观测与10个变量。各变量的意义及取值如表5所示。
我们提取其中的race、smoke、ht、ui、ftv这5个分类变量与离散变量来做分析,看看低体重产儿(low=0)的母亲与正常产儿(low=1)的母亲的这些指标之间是否存在差异。下面的图1至图5分别给出了两组产妇之间的这5个指标的分布差异对比图。从这些图中,我们可以看到,低体重产儿的产妇与正常产儿的产妇之间的这些指标的分布有明显的差异。比如,相比正常产儿的母亲,低产儿母亲中黑人比例、吸烟比例、有高血压史的比例、存在子宫刺激的比例以及在怀孕前三个月未看过医生的比例都偏高。下面我们采用本文提出的方法与经典的卡方检验来检验两组样本的这5个分类变量的联合分布的差异。

表5 birthwt数据集中各变量名称及其意义与取值
显然,两组的race、smoke、ht、ui与ftv这5个变量的联合分布都是取值在3×2×2×2×7=168个类别上的离散分布,理论上的联合列联表为2×168的二维表,但由于单元格中大部分元素为0,去掉整行或整列为0的行或列后,只剩下2×46的列联表。此时,我们采用卡方检验对此列联表做独立性检验,可得卡方统计量的值为54.688, 相应的p值为0.1527.这说明,卡方检验结果显示,低体重产儿的产妇与正常产儿的产妇之间的这5个分类指标的联合分布没有明显的差异。接下来,我们采用本文提出的Tm,n重新对两组的5个分类指标的联合分布做差异性检验,可得统计量的值为 28 447.99,在499次置换样本的情况下,得到相应的p值为0.024.因此,我们的方法说明,低体重产儿的产妇与正常产儿的产妇之间的这5个分类指标的联合分布是有明显的差异的,这跟图1至图5展示的结果是一致的。

图1 低体重产儿与正常产儿的产妇的种族分布对比图

图2 低体重产儿与正常产儿的产妇是否吸烟的分布对比图


图5 低体重产儿与正常产儿的产妇是在怀孕前三个月看医生次数的分布对比图
5 总结
本文基于独立随机向量的能量距离(ED)的概念给出了分类变量(向量)的能量距离(ED)的定义,由此给出了一种新的检验两个分类变量(向量)的分布差异的检验统计量。该检验方法的检验统计量只涉及两组样本频数的差距,因此计算非常简便,且适用于任意有限维的分类的随机向量。数值模拟结果说明,在小样本或类别变量较多的情形下,该方法比经典的卡方检验法能更好地控制第一类错误,同时具有更高的功效。
