水准网线性混合效应模型建立与参数估计研究
2022-09-27陈军红王炳燕
陈军红,王炳燕
(1.西安建筑科技大学华清学院 土工程学院,陕西 西安 710043;2.海南灵宇地理信息有限公司,海南 571138)
0 引言
随着各地城市建设加快发展,城市规模不断扩大,中高层建筑越来越多。在这种发展形势下,楼层的增加、荷重的增大,引起建筑物发生沉降变形的可能风险也加大。在建造与运营过程中,沉降测量发挥主要监测与保障作用,减少安全隐患发生[1]。在建筑物沉降监测方法中,水准测量是最常规,使用最频繁的方法[2]。文献[3]~[6]均表明,到目前为止,利用精密电子仪器,采用水准测量技术,依据工程作业规范,对建筑物实施沉降监测是工程实践中的普遍做法,被应用于不同类型的中高层建筑物的沉降监测。但由于受工程施工、外业观测保障措施不到位以及数据优化处理方法欠佳等诸多因素的影响,导致数据信息精度与可信度较低。根据沉降测量高精度监测要求,观测数据不能准确反映建筑物的沉降量实际情况。本文主要对现有水准测量数据平差处理中存在的不足,进行改进处理,提高沉降观测数据的精度。
在水准网测量数据处理环节中,针对测量误差,正确定权是参数估计的重要一步。一般做法,依靠水准路线长度、测站数以及定权数学模型。实践中发现,不同定权方法对估计结果影响很大,结果之间存在较大差异性。文献[7]以实例说明,水准控制网的观测数据按照测段距离与按测站数定权平差存在差异。且对建筑沉降观测而言,按照测段距离定权平差并不合适,而按照测站数定权平差计算,既有失权比之间的准确性,又严重影响参数估值的精确性。针对此问题,本文摒弃定权的常规思维,另辟蹊径,从水准网误差方程出发,对路线长度与高程两变量之间的函数关系重新研究。尝试基于微分思想与中值定理,建立水准网线性混合效应模型,使用最小二乘法统一理论进行参数估计。经过模拟试验以及工程案例分析,结果表明,水准网利用线性混合效应模型进行平差计算较传统间接平差具有无需定权、参数估计精度高、沉降趋势特征明显等优势,为其应用与推广奠定理论基础。
1 模型建立与参数估计
1.1 模型建立


图1a 水准网示意图

(1)
依照微分中值定理的几何意义可知,f′(ζ1)为切线斜率,如图1b所示,ζ1处切线e′f′与直线mn平行。但若测量数据含有误差,导致切斜e′f′有θ1角偏转,切线e′f′旋转到ef处。记直线ef倾斜角α1,则改正后切线e′f′倾斜角α1-θ1,斜率tan(α1-θ1)。则利用三角函数和差角公式与泰勒公式,可得(2)式。
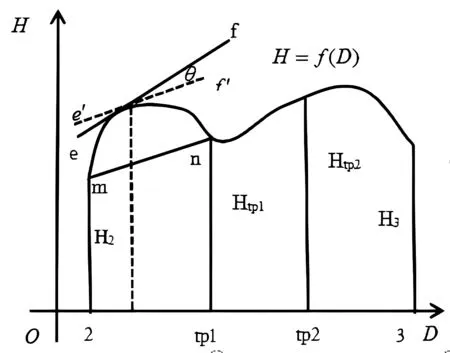
图1b 水准网测段D-H函数关系

(2)


(3)
同理。第二、三测站改正高差

(4)
将第一、二、三个测站高差求和,则测段2-3的改正高差

(5)

(6)
写出水准网所有测段A-2、2-3、B-1、1-3、3-C的改正高差

(7)
写成矩阵形式:

(8)
从而,概括水准网线性混合效应模型,可用(9)表示:
y=Ax+Bk+Cε
(9)
其中,y为观测量Y与待定高程近似值的差值,x为固定效应,k、ε为随机效应,假定满足正态分布,均值E(k)=0,E(ξ)=E(k2)≈σ2[1,1,…,1]T,σ2一般是10-6左右(参照模拟算例),可近似看成0,E(y)=Ax.k、ε具有相关性,联合方差

(10)
即
(11)
1.2 待定点高程估值与w权重的确定



(12)


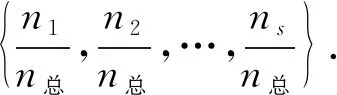

(13)
1.3 参数估计
1.3.1 固定效应的最小二乘估计 对于水准网线性混合模型y=Ax+Bk+Cξ,令V=y-Ax=Bk+Cξ,V~N(0,∑),则

(14)
一般情况下,M是正定矩阵[9],即
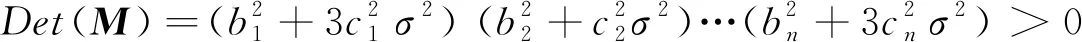
(15)
依据最小二乘法统一理论,可构造Q(x,σ)函数,

(16)
进行如下线性变换

(17)

(18)
根据普通最小二乘法原理,得到LS解

(19)

所以

(20)

图估计算法流程图
2 模拟试验
为检验水准网混合效应模型的平差计算有效性与优势,本文模拟实际施工现场,在室内进行试验,将试验结果与传统算法进行比较。试验设计过程如下:
1)采用某沉降监测工程中某条单一闭合水准路线,除观测高差h以外其他数据不变,包括起算数据HA、测站数ni与测站视距Di(i=1,2,…,50),具体数据如表1.

表1 模拟试验起算数据与其他数据
2)利用函数H=HA+A*sin(2π*Di/D总),A=0.003(D总为水准路线总长)插入50个高程点,计算出每个点的高程真值Hi,包括模拟沉降观测点HB=37.4979m、HC=37.6849m、HD=33.7414m、HE=32.0109m.利用相邻两点高程真值求得每测站高差真值hij=Hj-Hi(i≠j).


4)采用模拟观测数据,建立线性混合效应数学模型,按照最小二乘算法对模型参数进行估计,结合参数值,计算出B、C、D、E四个点高程估计值。
5)B、C、D、E四个点高程估计值与真值比较,算出之间的不符值VB、VC、VD、VE,


表2 试验结果比较(间接平差)
从表2与表3、图3(为突出数据差异性与数字表示清晰,图3a数据扩大1 000倍,取一位小数)对比可看出,水准网采用线性混合效应模型平差计算,结果更优。第一,残差方差估计值更小。传统算法的方差估值处于1.41~4.73 mm2之间,而线性混合效应模型则在0.05(10-6)~7.45(10-6) mm2之间。第二,在同一种观测条件下,线性混合效应模型平差结果相比较真值,误差更小,估值精度高,即沉降观测点的高程估值更接近真实值。比如在编号6的观测条件下,线性混合效应模型估计精度为2.22 mm2,而传统算法为115.12 mm2.第三,在非相同观测条件下,观测精度越高,线性混合效应模型的估计精度越高,优势越明显。比如,编号4比编号5的估计精度多了6.66 mm2.第四、传统平差方法平差结果受距离或测站定权的因素影响,估计精度表现出差异性。而线性混合效应模型无需定权,完全避免这种因素影响,估值只与外业观测条件有关。总之,对于精密水准测量(尤其沉降观测工作)来说,采用线性混合效应模型进行平差计算更为合适。

表3 试验结果(线性混合效应模型)

图3a 参数估计真误差对比

图3b 残差方差估计与参数估计精度对比
3 建筑物沉降观测数据处理与分析
3.1 工程概况与施测工作
该建筑物位于新疆地区某路人群密集地段,占地5万平方米,建筑面积8 453平方米,为地上6层、钢筋混凝土框架结构。因管线跑水造成地基下沉,建筑物中部以及西部墙体多处出现裂缝。现需通过监测建筑物底部各结构点的沉降量、沉降差值及沉降速度,预测沉降发展趋势。根据现场实际情况与规范要求,5个基准点均布设在建筑物的沉降区域之外的安全地点。监测点的埋设采用深埋加基础底盘现浇的方法,深度约为15~20 cm.根据建筑物特点,在其上共布设18个观测点(编号从J1~J18),均布设在距离地面0.5 m高左右的墙柱上。基准点与观测点分布情况详见图4.

图4 基准点及沉降观测点布置图
监测网按照一等水准规范要求施测,5个监测点组成一条闭合的环形线路,基准0点为起始高程点,H0=835.3705 m.沉降观测点的施测组成环形线路,按规范二等水准技术要求进行施测。15天一周期,共测40 个周期,测量成果各项限差均符合技术要求。
3.2 数据处理方法与结果对比分析
每期数据都采用间接平差与线性混合效应模型进行平差处理,求得每期J1~J18沉降观测点的高程估值。根据相邻两期高程估值的变化,计算沉降量、累计沉降量、沉降速率等数值,依据数据绘出累计沉降量图(图5a)、沉降累积量与时间关系图(图5b)、沉降观测点速率变化图(图6)。通过对图5b观察,发现沉降观测点表现出明显直线下降趋势,于是对沉降累积量最大的J11点,通过一元线性回归方程进行拟合,求出沉降预测方程。

间接平差模型

线性混合效应模型

图6 沉降点速率变化(间接平差模型(左)/线性混合效应模型(右))
从图5、图6、图7比较可以看出,采用上述两种方法平差计算,1)沉降观测点高程估计存在一定的差异性,而且这种差异会引起沉降量、沉降累积量、沉降速率等计算量的不同。2)与传统算法相比较,通过线性混合效应模型计算的沉降观测点高程估值以及用估值计算的沉降量、累计沉降量与沉降速率,受误差影响较小,沉降趋势特征明显。3)通过两种方法计算的观测高程估值,虽然存在一定程度的差异,但不影响建筑物下降趋势特征的判断。但是会影响到预测方程以及预测结果,比如,预计J11点在615天的累计沉降量,传统算法结果为31.18 mm,新算法为28.87 mm,之间有2.31 mm的差别。这点差别不容小觑,因为时间越长,这种差别更大,最终会影响建筑物倒塌临界点的判断,应予重视。

图7 两种方法沉降预测差异对比
4 结束语
本文提出的线性混合效应模型以及参数的确定方法为水准网平差计算增加了一条新的途径。本文通过模拟试验以及沉降监测数据处理与分析表明,水准网线性混合效应模型较传统间接平差模型具有无需定权、参数估计精度高、沉降趋势特征明显等优势。另外,二维、三维空间是否也存在线性混合效应模型,有待进一步探讨与研究[11,12]。
