改进的边坡最小势能法及潜在滑动方向研究

2022-09-23温树杰赖光甜孙自立

铁道科学与工程学报 2022年8期

温树杰，赖光甜，孙自立

(1.江西理工大学土木与测绘工程学院，江西赣州 341000；2.江西理工大学江西省环境岩土与工程灾害控制重点实验室，江西赣州 341000)

最小势能法用来分析边坡稳定性最先由MAULDON等[1]提出，按照坡体发生位移时势能最小的原理进行坡体的稳定性分析。不需要对滑体划分成许多条块，大大避免了迭代计算，具有计算过程简单、容易编制程序和便于工程应用等优点。但当时最小势能法的适用性较窄，李小强等[2-4]看到了最小势能法在分析边坡稳定方面的优势，开始不断地完善。将最小势能原理推广运用在一般的二维边坡和非稳定非饱和渗流下边坡的稳定性分析等方面，并验证了其具有合理性。但以上的研究工作，在计算势能时都没有考虑滑裂面上的剪切势能，实际情况中剪切势能真实存在。温树杰等[5]引入了一些假设通过定义主滑面确定滑裂面上剪力的方向，考虑了滑裂面上的剪切势能，使计算的安全系数和其他方法得到的结果更接近；蒋建国等[6]将改进的最小势能法运用于水平-竖向立体筋边坡稳定性分析，沿虚位移方向建立平衡方程得到剪应力，进一步得到线弹性范围内剪切势能函数。这些学者认识到了考虑剪切势能的重要性，先通过平衡方程求解剪力和剪应变，再进一步计算剪切势能，但当滑体受到的外力较多时，会导致解方程变得困难，所以，有必要发展一种简洁且合理的剪切势能计算方式。孙加平等[7-8]运用最小势能法研究滑体整体滑动方向，指出将虚位移方向作为潜在滑动方向还要讨论；郭明伟等[9]提出了边坡的3种整体下滑趋势方向，并表明定义不同的下滑趋势方向得到不同的矢量法安全系数；刘素锦等[10]采用最小势能原理得到了边坡的主滑方向，认为主滑方向对边坡整体稳定性的评估有着直接的影响。本文对边坡滑体的潜在滑动方向进行进一步的探索。前人的研究表明用最小势能法评估边坡的稳定性是可行的，同时极大地促进了最小势能法在边坡稳定性分析方面的发展和应用。本文基于最小势能法现有的研究工作，给出了计算滑体系统弹性势能的新方式，根据功能原理直接计算弹性压缩势能和剪切势能，提出了改进的最小势能法，并通过对比分析4种可能的潜在滑动方向，给出了推荐采用的潜在滑动方向。相比以前的工作，文中方法计算剪切势能时无需引入假设，通过岩土体弹性模量E和泊松比μ可直接得到剪切势能，计算过程简洁，便于安全系数的求解；此外，确定了推荐采用的潜在滑动方向，解决了对于不同的潜在滑动方向最小势能法所得安全系数不一致的问题，便于推广应用。

1 基于功能原理的势能计算

图1所示为边坡势能计算模型示意图，滑裂面方程为y=f(x)。运用最小势能法分析边坡稳定性时，将滑体刚度视为无限大而滑床是弹性的，在合外力R=(Rx,Ry)作用下，滑体发生一个虚位移d=(dx,dy)后边坡处于稳定平衡状态，认为此时边坡系统的总势能最小，同时系统储存了弹性压缩势能和剪切势能[2-3]。图中，i代表滑裂面上某一微单元，Li是微单元i的长度，Ni和Ti分别为滑裂面某一微单元i上的法向力和剪力。

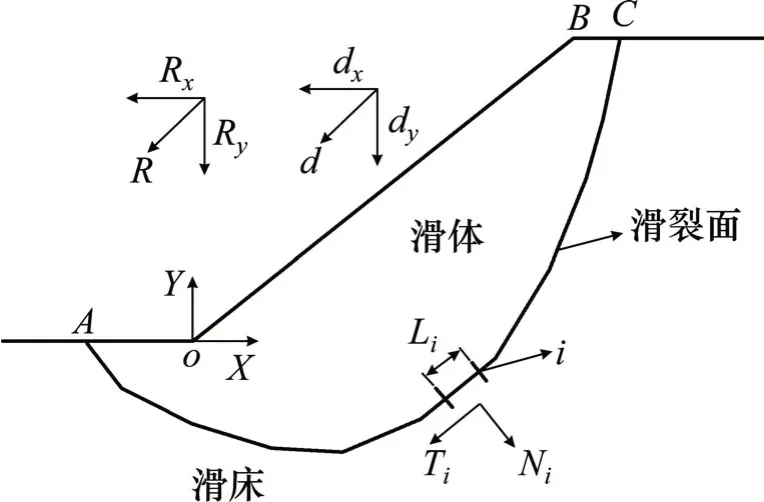
图1 边坡势能计算模型Fig.1 Slope potentialenergy calculationmodel

1.1 弹性压缩势能计算

根据功能原理求解弹性压缩势能，计算示意图如图2所示，Δhi是微单元i上的压缩变形量，n i=(nxi,nyi)是外法线方向单位向量[5]，指向压缩变形方向，nxi和nyi分别是n i在X轴和Y轴方向上的分量，h是滑床上微单元受变形扰动的深度。

图2 弹性压缩势能计算示意图Fig.2 Schematic diagram of elastic compression potential energy calculation

微单元i上的压缩变形量等于虚位移在外法线方向上的投影：

微单元i上弹性压缩变形储存的弹性压缩势能为：

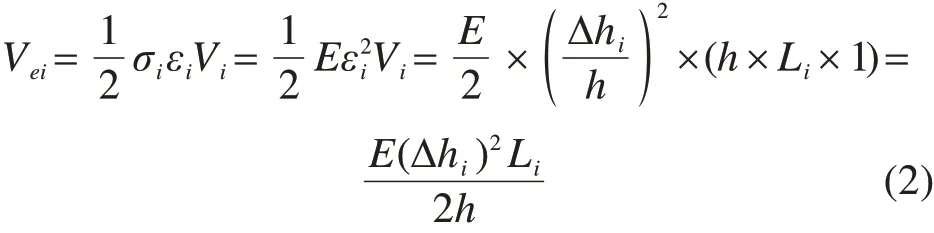
式中：σi和εi分别是微单元i上的法向应力和应变，，E是弹性模量，Vi是微单元i的体积。

把式(1)代入式(2)得：

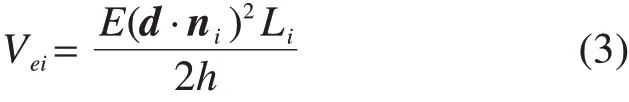
对滑裂面上所有微单元体的弹性压缩势能进行求和，得到总的弹性压缩势能：

1.2 剪切势能的计算

当前最小势能法计算剪切势能的方式是：在某个计算方向上通过力的平衡得到剪应力的表达式，进一步得到剪切势能的函数表达式，但当合外力较多时，会导致剪切势能表达式复杂，不利于虚位移的求解。因此，本文给出了一种剪切势能新的计算方式。示意图如图3所示，ΔLi是微单元i上的剪切变形量，t i=(txi,tyi)是外切线方向单位向量[5]，指向剪切变形方向，txi和tyi分别是t i在X轴和Y轴方向上的分量，h是滑床上微单元受到扰动的深度。

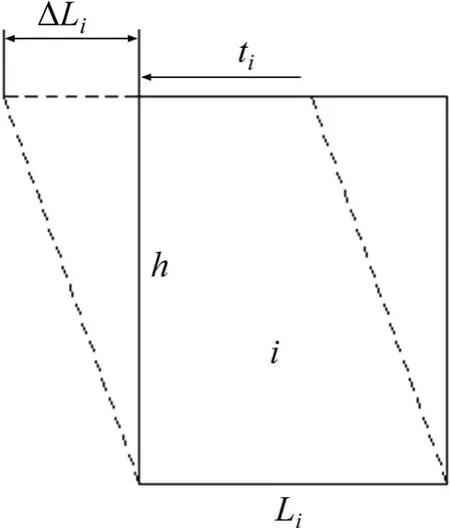
图3 剪切势能计算示意图Fig.3 Schematic diagram of shear potentialenergy calculation

微单元i上的剪切变形量等于虚位移在剪切变形方向上的投影：

微单元i上剪切变形储存的剪切势能为：

式中：τi和γi分别是微单元i上的剪应力和应变，τi=Gγi。微单元体发生的扰动位移很小，所以近似认为G为剪切模量，Vi为微单元i的体积。

把式(5)代入式(6)得：

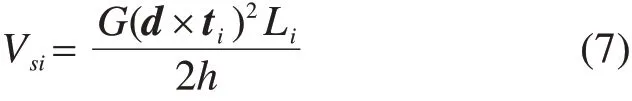
剪切模量G与弹性模量E有如下关系：

式中：μ为泊松比。

把式(8)代入式(7)得：

滑裂面上所有微单元体剪切势能的总和为：

2 虚位移及滑面上力的计算

2.1 虚位移求解

滑体的总势能来源有3个方面，滑裂面的弹性势能，滑床的剪切势能，合外力做功，则总势能为：

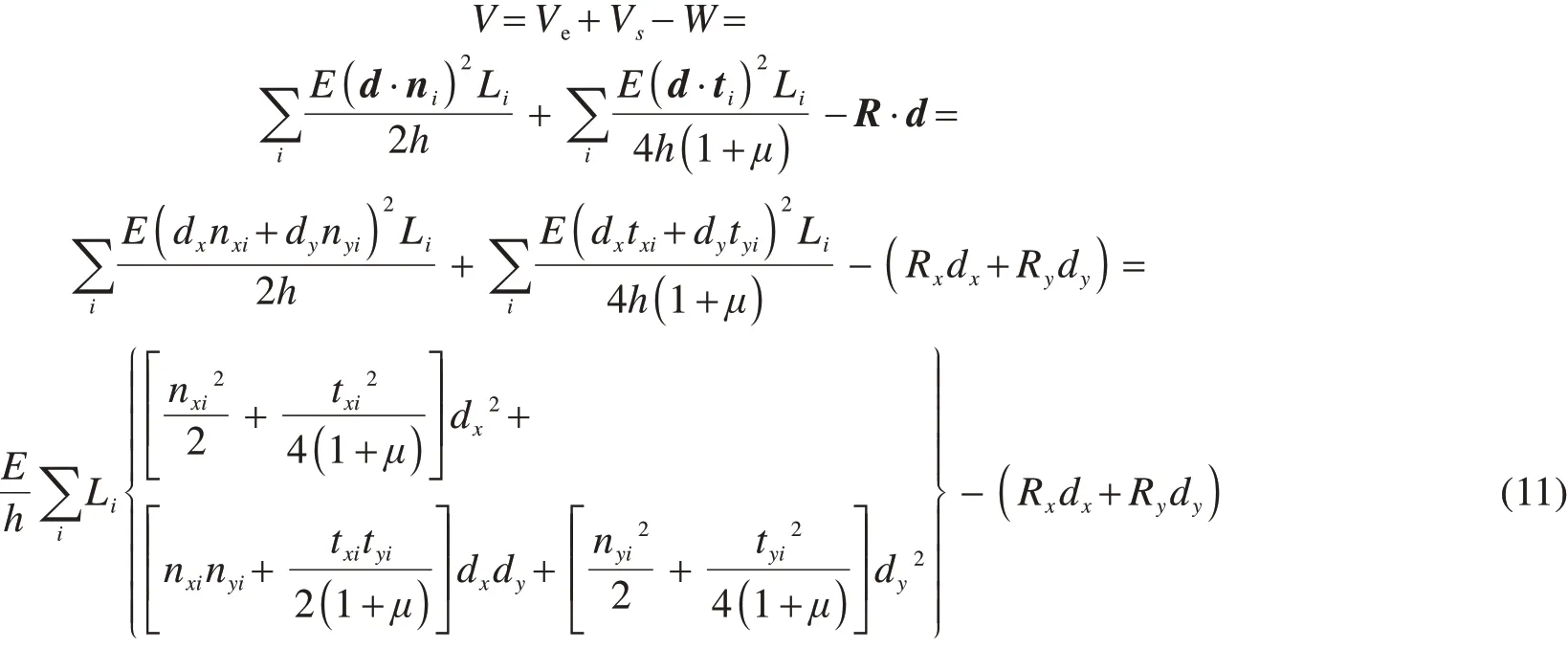
基于最小势能原理，此时边坡的总势能最小，可以求得对应的虚位移：

由式(12)可得：

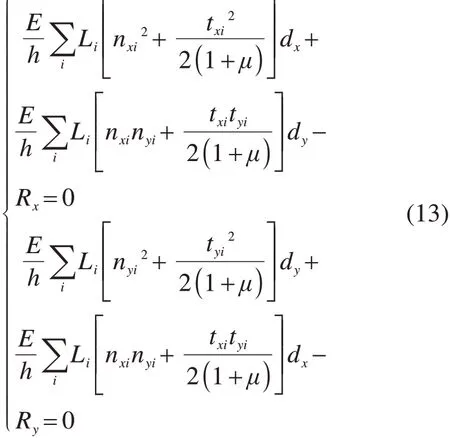
为了简化计算，引入λ：

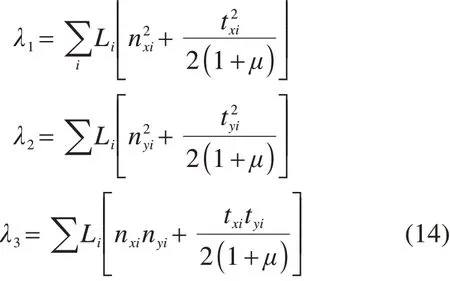
将式(14)代入式(13)中：

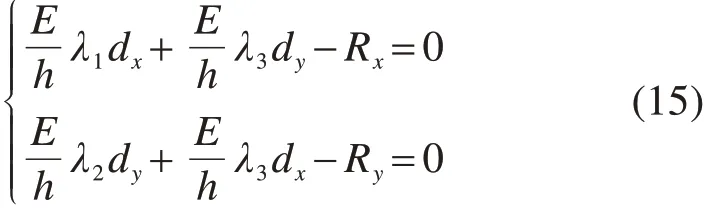
求解式(15)，虚位移最终可得：

2.2 滑面上力的计算

滑面微单元i上的法向力Ni为：

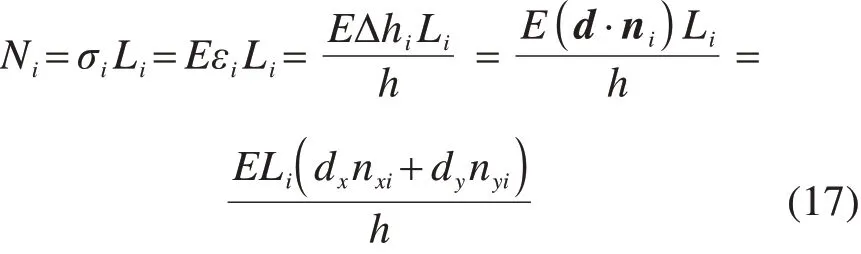
滑面微单元i上剪力Ti表示为：

由莫尔库伦准则可得滑面微单元i上的抗剪力为：

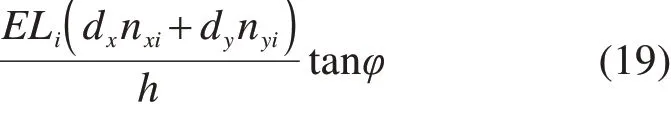
式中：c是岩土体的黏聚力；σ′i是微单元i上滑床作用于滑体的反向法应力，在数值上与σi相等；φ是岩土体的内摩擦角。

3 安全系数的计算

安全系数是边坡稳定性评价的一个关键指标，边坡安全系数的计算方式有很多种，众多学者[11-13]开展了计算安全系数的探究工作。对比了多种方法，本文以滑体沿潜在滑动方向上的抗滑力与下滑力之比计算安全系数[13]。抗滑力由滑床对滑体产生的法向反力和抗剪力在潜在滑动方向上的分量组成，下滑力是合外力在潜在滑动方向上的分量，这种定义方式意义明确。

安全系数K可按下式计算：

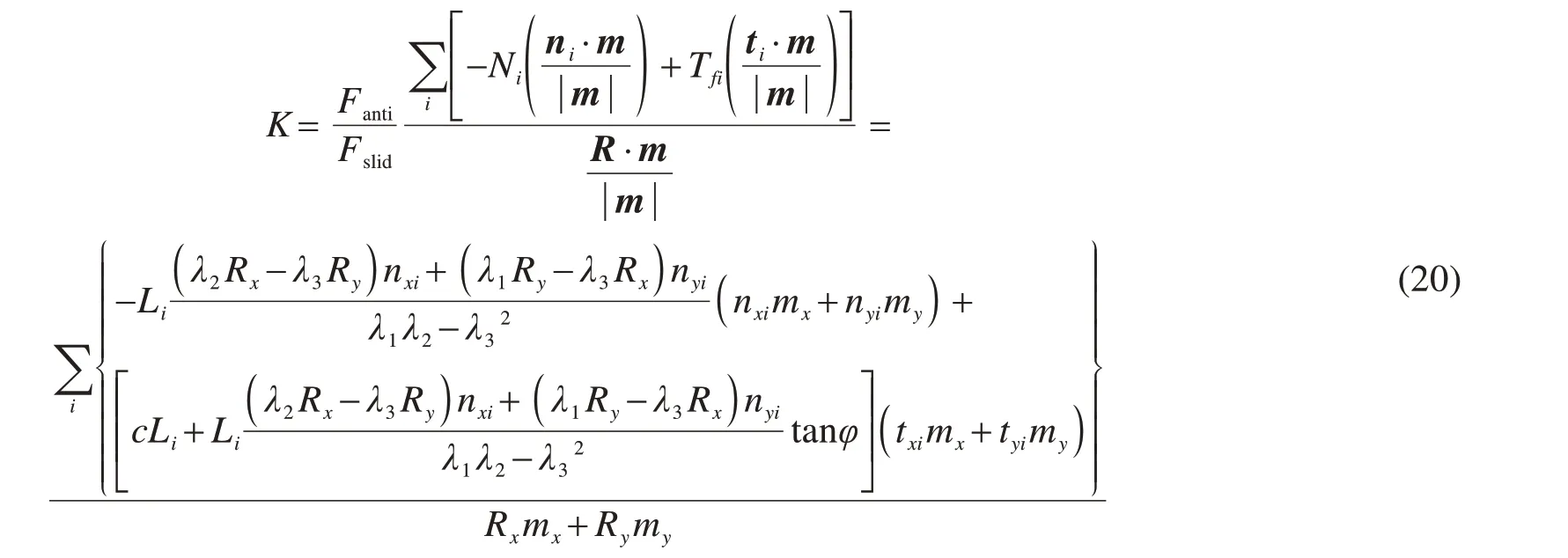
式中：Fanti为抗滑力；Fslid为下滑力；m=(mx,my)为滑体潜在滑动方向。

上式中滑体潜在滑动方向还是未知的，通过查阅文献[9-10]，列举出边坡4种可能的潜在滑动方向。

1)剪入点到剪出点方向

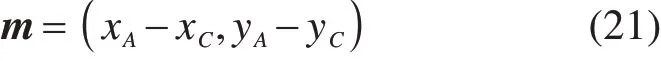
式中：(xA,yA)为滑面上剪出点坐标；(xC,yC)为滑面上剪入点坐标。

2)滑体虚位移方向

3)滑面上抗剪力矢量和反方向

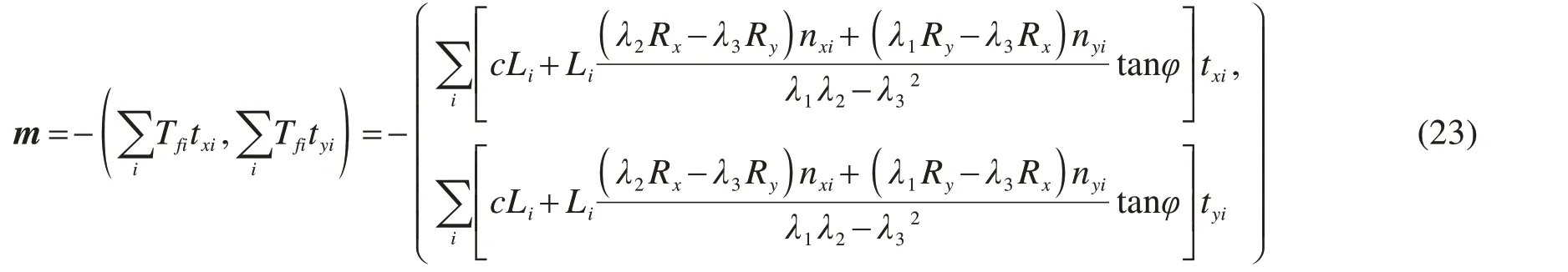
4)滑面上剪应力矢量和方向

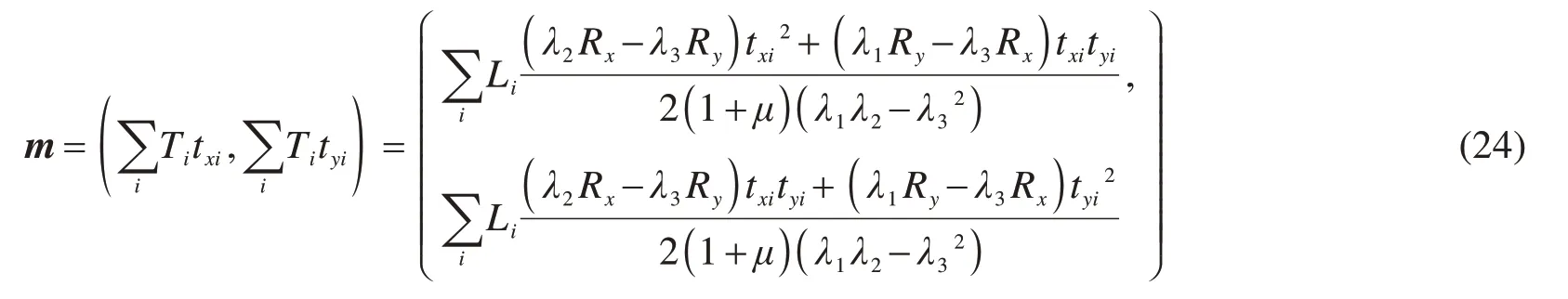
将式(21)，(22)和(24)分别代入式(20)，即可得到不同潜在滑动方向的安全系数。

4 算例分析与考题验证

4.1 滑体潜在滑动方向的探讨

根据文献[7,9]发现，计算安全系数时选取不同的潜在滑动方向得到的结果都是不一样的，因此为了确保计算的安全系数是可靠的，必须确定合理的潜在滑动方向。引入4个均质圆弧滑面边坡的经典算例和1个折线型滑面的边坡算例，这5个算例[2,13-15](见图4)被较多学者用在验证边坡稳定性分析方法的合理性。利用开发的安全系数计算程序，输入各算例的边坡及滑面参数，计算中泊松比取0.3，得到了各算例采用文中方法在4种可能的潜在滑动方向的安全系数(见表1)。极限平衡法作为工程实践中使用最广泛的方法具有代表性，所以本文将传统极限平衡法的结果作为参考值与改进的最小势能法计算结果对比分析，探讨滑体合理的潜在滑动方向，根据文献[2-3,13-15]得到5个算例采用简化Janbu法和简化Bishop法的安全系数(见表1)。

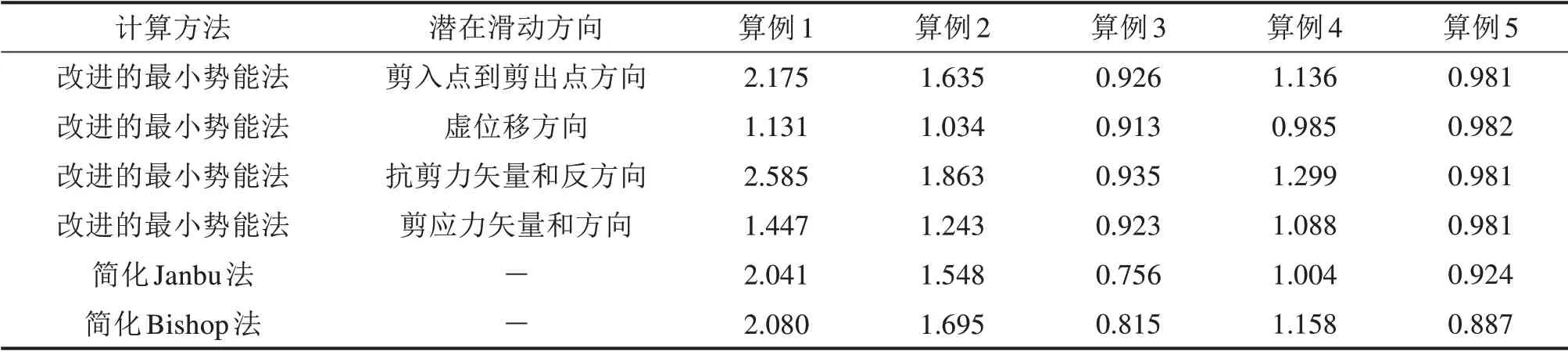
表1 各潜在滑动方向对应的安全系数与极限平衡法结果对比Table 1 Comparison of the safety factor corresponding to each potentialsliding direction and the resultof the lim itequilibrium method

图4 各算例边坡剖面形状及边坡参数Fig.4 Slope section shape and slope parametersof each example

从表1的数据可以看出，算例3，4和5中根据改进的最小势能法计算的安全系数和传统极限平衡法的结果基本接近。程序显示，算例3和4中在整个滑面上产生的抗剪力在4种潜在滑动方向上力的分量都是阻止滑体下滑的效果，下滑力的方向也是不变的，所以计算的安全系数变化不是很大；算例5中在各种可能的潜在滑动方向计算的安全系数看似基本相等，是由于4种潜在滑动方向与水平方向形成的夹角很接近，导致计算的安全系数前几位有效数字是一样的。算例3，4和5的计算结果表明了本文改进的最小势能法分析边坡稳定性是合理可行的。

对比算例1和2根据改进的最小势能法计算安全系数的结果，发现4种潜在滑动方向对应的安全系数之间有较大的变化。原因是：若按虚位移方向计算算例1和2的安全系数，虚位移方向与水平方向形成的夹角相比其他3种潜在滑动方向与水平方向形成的夹角是最大的。部分滑床对滑体产生的抗剪力在虚位移方向上力的分量发生了反向，使得总的抗剪力减小，而下滑力的方向是不变的，因此沿虚位移方向计算的安全系数减小。再对比其他3种潜在滑动方向，发现算例1和2分别按照抗剪力矢量和反方向和剪入点到剪出点方向计算的安全系数更接近传统极限平衡法。

上述5个边坡算例具有一定的代表性，不仅包含了形状、尺寸和物理力学参数各异的圆弧滑面边坡也有折线形滑面的边坡。且极限平衡法作为边坡工程中最常用的稳定性分析方法，计算的安全系数具有一定的说服力，所以常被用来作为其他算法的参考值。综合上述5个算例对比分析，发现沿其中2种方向计算的安全系数最接近传统极限平衡法结果，分别是抗剪力矢量和反方向和剪入点到剪出点方向。但是从运动学的方向考虑，边坡滑体在自重作用下会沿着阻力最小的方向滑动，而边坡丧失稳定性时在土体中形成的连续的滑动面就是最危险滑动面，在此临界状态下滑动面上各点的剪应力都达到了土的抗剪强度。由于坡体滑动方向与抗剪力方向是相反的，所以把滑体的潜在滑动方向视为该滑动面上抗剪力矢量和反方向是符合常理的。并且根据这个方向计算的安全系数也非常接近传统极限平衡法的结果，所以本文推荐采用抗剪力矢量和反方向作为滑体的潜在滑动方向。

4.2 考题验证

为了进一步验证本文计算方法和推荐采用的潜在滑动方向的合理性，选择澳大利亚计算机应用协会(ACADS)发布的10道边坡稳定分析考题中有较强代表性的EX1(a)考核题[2]，边坡的材料参数见表2。

表2 考题EX1(a)材料性质Table 2 Exam question EX1(a)Materialnature

考题要求确定临界滑裂面和最小安全系数，利用边坡稳定性分析软件选取简化Bishop法求出最危险圆弧滑动面的位置，得出安全系数为0.985。发现计算所得的临界滑裂面(形状和参数见图5)与各个裁判程序求得的临界滑裂面[2]都落在一个很窄的区域内，并且计算的安全系数与推荐的裁判答案1.000很接近。所以，本文采用此临界滑裂面作为考题的滑裂面，再用文中改进的最小势能法计算考题的安全系数，验证本文方法是否合理，将安全系数计算结果列于表3。

图5 程序计算ACADS考题EX1(a)的临界滑裂面Fig.5 Program calculates the criticalslip surface of ACADS testquestion EX1(a)

表3 考题EX 1(a)安全系数计算结果Table 3 Testquestion EX1(a)safety factor calculation result

由表3的数据可知，本文改进的最小势能法计算的安全系数与推荐的裁判答案1.000相差6.8%，差值在合理范围内，表明了本文改进的最小势能法和确定的潜在滑动方向在边坡稳定性分析中是合理的。

4.3 泊松比对安全系数的影响分析

从文献[16]中发现，有限元安全系数随着泊松比的调整其大小发生了变化。和弹性模量E一样，泊松比μ也是材料固有的弹性常数。根据热力学原理，不同岩土体的泊松比不一样，岩土体作为常规、传统的材料，μ在0到0.5之间，当泊松比接近0.5时，材料是不可压缩的，类似于液体。为了分析泊松比的取值对改进的最小势能法和确定的潜在滑动方向的影响，将文中算例1-5的泊松比分别取0.1，0.2，0.3，0.4和0.49，计算的安全系数见表4。

由表4可知，5个算例中随着泊松比的增大安全系数略有增大，泊松比为0.49时相比泊松比为0.1时安全系数最大增幅在8.583%～13.086%之间，这是泊松比取极大值和极小值下的情况。然而在实际工程中，虽然根据岩土体的类别难以精确确定泊松比的数值，但选取的泊松比与岩土体真实情况下的泊松比在一个很小的区域内，计算得到的安全系数相差很小。从上可以得出结论，按文中改进的最小势能法计算安全系数时不同的泊松比对应的安全系数不一样，但在实际工程中泊松比只要按岩土体类别在合理范围内取值，就对计算结果影响很小，采用本文方法得到的边坡安全系数是可行的。