基于FFT的感应测井信号频谱分析软件设计

杨晨，吴银川，曹亢

西安石油大学 陕西省油气井测控技术重点实验室（陕西 西安 710065）

0 引言

感应测井技术是现阶段我国在石油开采过程中应用最广泛的一项技术[1]，该技术通过发射不同频率下的激励信号来对应不同地层的探测深度，当采用多种频率信号同时激励时，在加快勘探进程的同时还可以得到地层的多维信息从而提高精细勘探能力[2]，其中接收传感器的精密检测是感应测井仪器设计的关键技术之一。常见的幅度相位检测方法有相敏检测和快速傅里叶变换两种[3]，相敏检测技术是通过锁相检测确定频率信号的幅度和相位，在实时检测系统中可实现边采集边计算，不需要大量的内存空间，实时性好。但根据相敏检测原理可知在进行多频信号检测时，每1次检测只能检出1种频率信号的幅度和相位，几个频率的信号则需要做几次相敏检波，因此效率不高。快速傅里叶变换（FFT）作为传统的频谱检测方法，具有原理简单易实现的特点，是数字信号处理中频谱分析最常用的方法[4]，并且可一次检测出多种频率信号的幅值及相位，提高检测效率。

本文基于感应测井技术的特性，研究设计了基于FFT的阵列感应信号测量分析软件。阐述了软件实现信号频谱计算的原理，推导了FFT算法实现信号频率、幅值、相位公式，测试并分析了在噪声环境下进行整周期和非整周期采样时，软件检测结果的误差范围；基于检测结果，量化分析了软件的精确度和稳定性。

1 信号频谱计算原理

1.1 信号频谱计算的方法

本文采用FFT方法对信号频谱进行检测，目前面向实际应用层面，基2和基4 FFT算法是使用最广泛的FFT算法[5]，其中基4时分FFT算法的复数乘法为基2时分FFT算法的3/4，但基4时分FFT算法较基2时分FFT算法可变换的数据长度更少，灵活性较差。为使软件具有更广泛的数据处理宽度，本文采用DIT-FFT（基2时间抽取快速傅立叶变换）算法来实现正弦信号的频谱分析要求。基2 FFT算法是利用旋转因子的对称性，将有限长序列不断进行奇偶抽取，直至分解成长度等于2的短序列，最终只需计算长度等于2的短序列的DFT变换[6]。

1.2 频谱计算的具体实现

设被测信号为：

式中：A为信号幅度，V；f0为信号频率，Hz；θ是信号初相位，（°）。

在满足奈奎斯特采样定理的情况下，以采样频率fs=1/Ts对信号进行采样，可得离散正弦信号为：

式中：n=0,1,2,…,N-1,N为采样点数。根据基2时分FFT算法性质采样点数N应满足2的整数次幂，对式中的N个采样点进行FFT运算，其变换结果见式（3）。

根据积化和差公式，可得式，令N=lfs，l为整数，可得式（4）：

则式（5）可化简为式（7）所示

根据离散正弦信号的周期性可知当lf0+k≠0时必为0；当lf0-k≠0时必为0。当lf0+k=0时，必有f0=k=0；当lf0-k=0时，有：

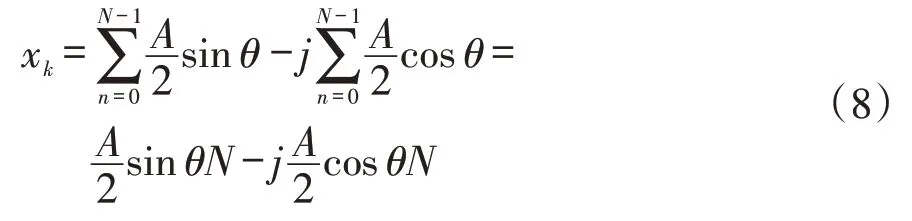
其中Ak是根据复数序列第k点所求得的幅值，V，采样数据经FFT变换后，生成的复数序列xk实部及虚部组成与被测信号相位的关系，见式：式中：θ为被测信号相位（°），信号频谱分析中频率值的计算与频谱分辨率有关，频谱分辨率是指频谱分析时能够分辨的两个频谱分量的最小间隔，频谱分辨率F与采样点数及采样频率有关，实际设计中应根据被测信号频率大小，设计采样点数及采样频率，防止频谱分辨率过大，以产生频谱泄露现象，分辨率公式如式（11）所示，根据频谱分辨率的概念，可推出频率轴第n点所代表的频率值为：

2 软件设计

2.1 软件界面和功能

本文基于Visual Studio 2015开发平台C#语言对软件进行开发与设计，C#语言是一种安全、稳定、简单易操作同时不失效率性和鲁棒性的面向对象编程语言[7-9]，软件设计框图及界面运行图如图1和图2所示。

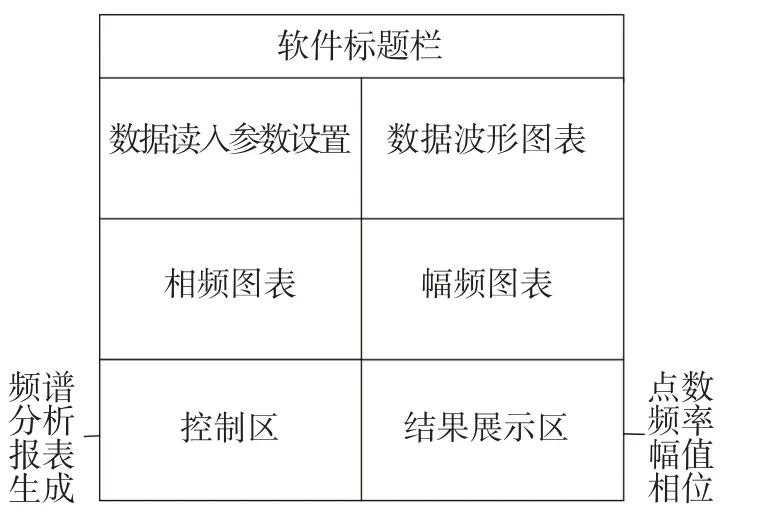
图1 设计框图

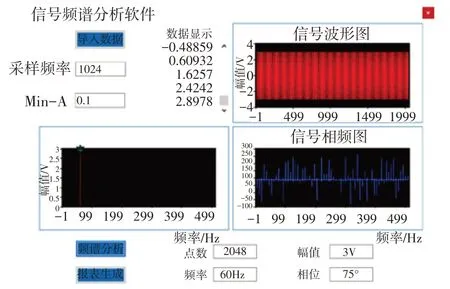
图2 运行界面

软件功能包含数据读取、频谱分析和报表生成，数据读取功能支持读入以TXT格式存储的正弦信号数据。频谱分析功能在精确测量被测信号频率、幅值和相位的同时生成幅频图和相频图，多正弦信号叠加情况下测量的频率、幅值和相位以空格分割显示。报表生成功能支持将信号幅频、相位值以及幅频图相位图存入用户指定文件中，软件默认以报表生成时间及当前读入数据点数及信号采样频率为文件命名。

2.2 数据文件读入方法

软件数据读取展示及功能流程图如图3所示。

图3 数据文件读取流程图

软件利用C#OpenFileDialog类实现在用户点击界面数据导入按钮时，软件界面弹出文件选择对话框，用户选定数据文件后软件逐行读取所选文件内容。采用VS中的Textbox控件显示读取数据的同时将数据存入到字符数组并计数，当读取的数据文件行内容为空时停止读取和计数，使用C#中的Convert类将字符型数组逐个转换为浮点型数组，遍历数组将数据点数作为chart图表数据源绘出数据波形图，完成数据读取、绘图和计数功能。

2.3 信号频谱计算

根据奈奎斯特采样定理，当采样频率fs大于有限带宽信号x(t)带宽f0的两倍时，信号可以由其采样值重构，否则信号会在x(n)中产生混叠，易得采样数据x(n)能表示的频谱最高模拟频率为fs2 Hz，因此本文幅频、相频图皆采用半边频谱。软件频谱计算整体流程图如图4所示。

图4 频谱计算整体流程图

通过软件界面选择数据文件读入采样数据，设置采样频率等参数，继而对读入的采样数据进行DIT-FFT运算得出复数数组，根据公式可得FFT算法变换后的复数序列（数组）xk与幅值序列（数组）Ak以及信号相位序列（数组）关系，利用公式（12）可得信号频率，使用峰值算法提取幅值数组各个峰值，将高于阈值的峰值保留下来，通过C#Array.In⁃dexOf方法峰值所对应的幅值数组序列号（相位数组序列号）提取出信号幅值和相位，利用式点数与频率分辨率的关系得出信号分量频率，为了消除软件采用的浮点型数据所带来的测量幅值的波动性，利用用户在软件中输入的信号测量阈值筛选掉干扰峰值，精确得出信号各分量幅频及相位数值。

3 实验结果及分析

3.1 实验结果

实验选用MIT阵列感应测井仪器[10]的26.325、52.65、105.3 kHz的3种频率信号进行软件仿真验证。采用随机高斯白噪声，取信噪比变换范围为5～30 dB，信噪比定义为信号功率与噪声功率之比。取信号采样频率为5 391.36 kHz，采样点数为2 048，所选参数满足整周期采样要求，测50次取其平均值作为最终检测值，观察整周期采样情况下的测量精度，幅值及相位检测相对误差（表1、表2）。其次取采样点数2 048，信号采样频率取3 080.777 kHz，测50次取其平均值，观察非整周期采样对检测结果的影响，见表3及表4。

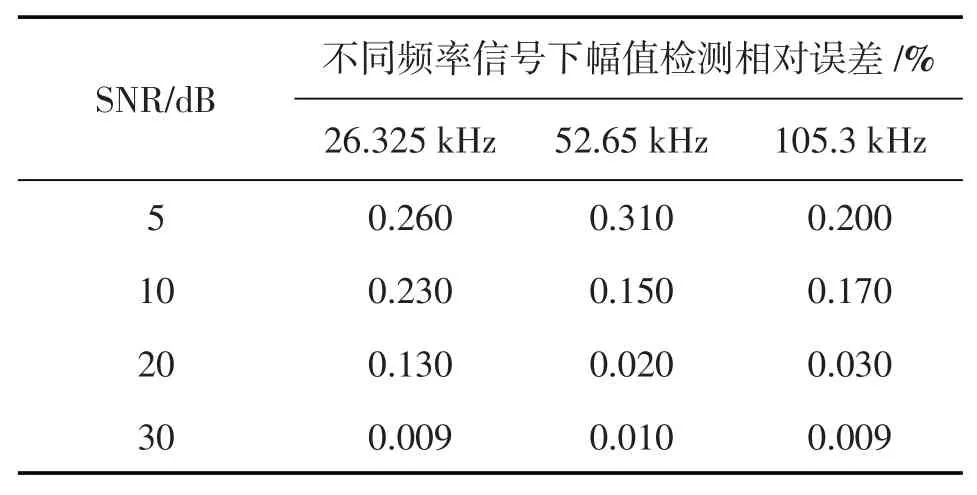
表1 整周期采样检测的幅值相对误差

表2 整周期采样检测的相位相对误差

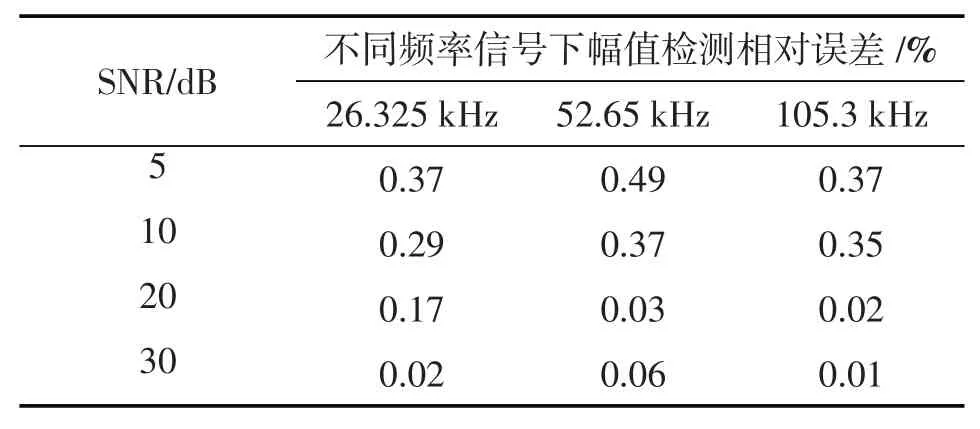
表3 非整周期采样检测的幅值相对误差

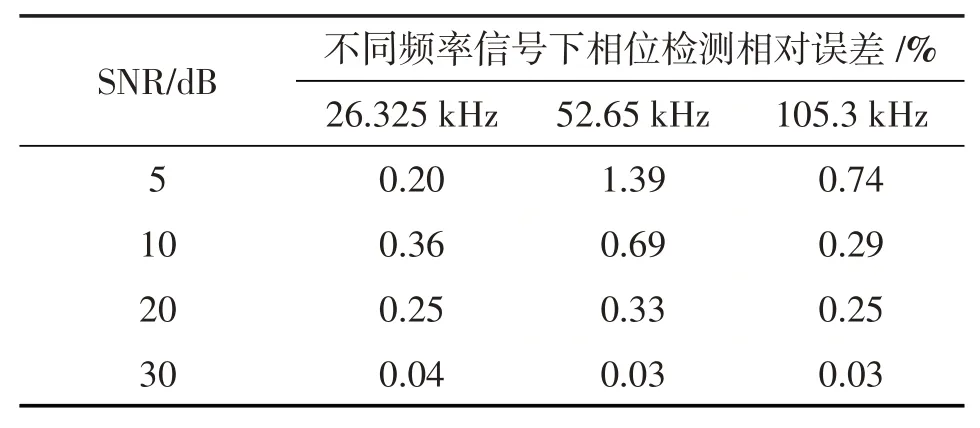
表4 非整周期采样检测的相位相对误差

3.2 结果分析

由表1及表2可得出,在满足整周期采样时，在软件信噪比低至5 dB的噪声环境下，当采样频率取5 391.36 kHz，采样点数取2 048，满足整周期采样的情况下，信号幅值检测相对误差不超过0.31%且相位相对误差不超过1.14%，验证了本文推导的FFT算法计算频率、幅度、相位等参数的理论计算公式准确性。通过表3及表4可得该软件在信噪比低至5 dB噪声背景下，当信号采样频率取3 080.777 kHz，信号采样点数不变的非整周期采样情况下，幅值相对误差不超过0.49%，相位相对误差不超过1.39%，相较整周期采样检测精度有所下降，但检测误差仍保持在1.39%以下，这表明该软件在噪声环境下以及非整周期采样等非理想情况下仍可实现信号频谱的精确测量分析功能。

4 结论

针对感应测井信号的处理与分析，设计实现了一种可量化分析信号幅频相位参数值的频谱分析软件，引入DIT-FFT、寻峰算法及C#语言构建软件频谱分析功能及软件界面。通过在噪声环境下以整周期及非整周期两种采样方式，对软件测量性能进行验证与分析。结果表明，该软件在信噪比低至5 dB的高噪声环境下，在整周期及非整周期两种采样方式下，软件测量的幅值及相位误差皆不超过1.39%，软件检测精度及稳定性高，满足实际工程使用要求，为测井信号数据分析提供了一种辅助手段。