基于模态试验的对接圆柱壳结构有限元模型修正

魏 莎，郑冰月，张 忠，李旭龙，陈立群

(1.上海大学 力学与工程科学学院，上海 200444；2.上海市应用数学和力学研究所，上海 200072；3.北京强度环境研究所 可靠性与环境工程技术重点实验室，北京 100076)

随着航空航天领域的迅速发展，圆柱壳结构因其特有的结构优势已得到了广泛应用[1-2]。为保证实际结构的安全可靠运行，往往需对其进行动力学环境试验。基于实际结构的试验预测结果真实可靠，是目前航天工程主要采用的预示方法。然而试验件存在制造周期长、成本费用高、操作复杂和试验环境难以搭建等问题。为解决上述缺陷，研究人员利用成熟的有限元软件进行数值模拟仿真。通过有限元软件进行仿真计算，可有效提高分析效率，节约研制成本[3]。然而，采用有限元仿真软件进行动力学预测要求有限元模型具有很高的近似精度，可以反映实体结构的力学特性。但是，仿真计算结果往往与实际试验数据存在一定的差异[4-6]。由于试验中存在的操作误差、测量误差和试验条件偏差等可通过规范试验人员的操作来减小，因此认为试验数据是准确可靠的。根据试验数据对有限元模型进行修正是一类广泛使用的模型修正方法[7]。有限元模型的误差包括模型阶次误差、模型结构误差和模型参数误差[8]。其中，前两种误差可通过精准建模和细化单元网格来控制。模型参数误差是模型修正主要考虑的因素。根据试验数据对有限元模型参数进行修正以缩小仿真和试验结果的偏差。基于试验数据修正后的有限元仿真模型具有较高的精度，可以代替实际结构进行分析计算和响应预测[9]。

根据不同的修正目标，有限元模型修正方法可分为基于静力试验、基于模态试验以及基于频响试验三种方法。其中，基于模态参数的修正方法将试验测试与仿真计算的模态参数之差作为目标函数对模型进行修正，是一类广泛使用的模型修正方法[10]。例如，苏忠亭等[11]基于模态试验和支持向量机响应面修正方法对火炮身管组件有限元模型进行修正。徐张明等[12]基于试验测试和预测的有限元模型得到系统频响函数，进而提出了一种改进的基于频响函数的模型修正方法。陈德朋[13]以某紧凑型轿车白车身为研究对象，采用响应面法对白车身有限元模型进行替代，并结合模态试验数据对模型进行修正，结果表明修正后的有限元模型精度明显提高，可用于后期的优化设计。

另一方面，根据修正算法的不同，有限元模型修正方法可分为基于有限元模型的灵敏度分析法以及基于数学模型的响应面法。基于灵敏度分析的方法将模态参数对修正参数的灵敏度表示为一阶泰勒级数展开的形式，进而构造特征量残差目标函数并采用优化算法对有限元模型进行修正。这种方法实际上是基于有限元软件不断迭代直至达到精度要求。对于复杂模型多次调用有限元计算会使效率大大降低。响应面法则是以显式的响应面函数来拟合结构特征量与修正参数之间的复杂隐式关系，通过建立一个替代有限元模型的代理模型进行优化迭代过程。这种方式可以避免多次调用有限元软件进行计算，从而保证精度的同时有效提高修正效率。麻越垠等[14]采用响应面法对叶栅摆动装置进行模型修正，修正后的前三阶模态频率误差均在1%以内。秦仙蓉等[15]分别采用二次多项式响应面和高斯径向基函数响应面模型对塔式起重机有限元模型进行修正，结果表明对于塔机结构，二次多项式响应面的拟合精度和修正效果比高斯径向基函数响应面更好。鲍诺等[16]采用响应面法对GARTRUR飞机有限元模型进行模型修正，结果表明修正后的模型在测试和预测频段具有良好的复现和预测能力。

本文以对接圆柱壳结构为研究对象，对结构进行模态试验获取模态参数并建立其对应的有限元模型，构建其二次多项式响应面模型，并利用构建的响应面函数替代有限元模型，实现对接圆柱壳结构的有限元模型修正。

1 对接圆柱壳结构模态试验

1.1 模态试验方案

试验所研究对接圆柱壳结构如图1所示，其基本参数如表1所示，采用6061铝合金进行加工制作。该结构由两个对称圆柱壳体连接在法兰基盘两侧，圆柱壳体与法兰盘在连接处采用焊接形式连接。法兰圆盘周向等距分布8个直径为12.5 mm的圆孔，圆孔在试验过程中用以螺栓连接两个带法兰圆柱壳。

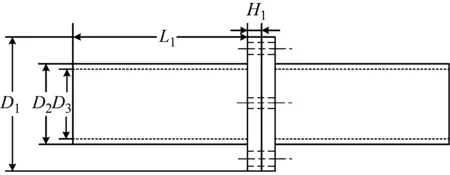
(a) 主视图

试验测试仪器选用LMS数据采集仪、B&K冲击锤和B&K三轴加速度传感器。模态试验过程采用单点激励多点响应的形式[17]，利用冲击力锤所施加的脉冲激励，采集各测点的响应信号，结合输入、输出信号进行曲线拟合，进而识别系统模态参数，模态试验测试系统如图2所示。本次试验采用弹性绳进行贯穿方式悬挂，以实现自由边界条件下的模态测试，悬挂方式如图3所示。模态试验中传感器测点的布置，根据工程经验结合预分析结果进行。在LMS Test.Lab软件中，总共划分112个测点，依次对测点进行x方向激励并进行5次有效平均，以保证能够激励出尽量多的模态。

图2 模态试验测试系统Fig.2 Schematic diagram of experimental modal test system

图3 模态试验方案及悬挂方式Fig.3 Modal test scheme and suspension mode of system

1.2 试验结果分析

基于上述试验测试方案，计算得到结构的前14阶模态频率与振型，结果如表2所示。模态阶次通过mode(m,n)描述，其中m表示轴向的节点数，n表示周向节点数，“*”表示结构振型呈轴对称分布。由表2可知，对于周向节点数相同的模态，模态频率有多组。此外，周向的半波数和轴向波数随着模态阶数的增加而增加，表现出圆柱壳结构的一般振动特性。但由于结构为对接形式，振型呈现出以法兰面为分界的对称振动和非对称振动。

表2 对接圆柱壳结构前14阶模态参数Tab.2 The first 14 order modal parameters of butted cylindrical shell structure

为了评价模态测试结果的正确性，通过模态置信度(model assurance criterion,MAC)进行评价。它是一种评价试验模态振型相关性的重要指标[18]，可以表示为

(1)

式中,φi、φj为模态振型向量。

MAC的取值范围为0～1，多数情况采用百分数表示。MAC值越接近于0，表示两个振型向量之间越不相关；MAC值越接近于1，则表示两个振型向量之间相似度越高。对于模态置信度矩阵而言，矩阵非对角线元素越小，各阶模态振型的独立性越好。图4给出了本次模态试验的MAC矩阵结果。由图4可知，MAC矩阵对角线元素接近于1，非对角线上元素都接近于0。这说明各阶模态振型均相互独立，试验模态测点选择和布置合理，试验模态分析得到的模态并无虚假模态。

图4 试验模态的MAC值矩阵Fig.4 MAC matrix of test mode

2 对接圆柱壳结构有限元建模

2.1 有限元模型

针对对接圆柱壳试验件，采用ANSYS有限元软件对其进行了有限元建模、网格划分以及动力学特性分析。在ANSYS中建立的有限元模型如图5所示，采用四面体单元划分网格，采用15 mm网格尺寸进行有限元网格划分，共划分32 639个节点，9 699个单元。对接圆柱壳的密度为2 750 kg/m3，弹性模量为71 GPa，泊松比为0.33，所采用的边界条件为自由边界。

图5 系统有限元模型Fig.5 Finite element model of system

在有限元建模过程中，法兰实体单元与圆柱壳壳体单元因为单元自由度不匹配，不能直接进行连接。在ANSYS Workbench有限元软件中提供了三种接触方式，六种接触类型。针对法兰SOLID186单元和圆柱壳SHELL181单元的连接接触面问题，选择面-面的手动接触绑定，连接界面采用罚函数算法[19]实现不同类型单元的连接。其中壳体端选用targe170单元，法兰端选用conta174单元来定义3-D接触对模拟。

2.2 有限元结果及对比

使用有限元软件ANSYS对结构进行模态分析，并采用Block Lanczos模态提取法[20]提取结构前14阶模态频率。与试验模态分析结果进行对比分析以确定有限元结果的准确性，模态频率的对比结果如表3所示。从表3中结果可以看出：对接圆柱壳结构的试验模态分析结果与有限元模态分析结果相对误差最大为6.33%，超出了可接受的误差范围。此外，由于实际结构和材料参数的误差波动，建立的有限元模型一般存在一定误差。因此，有必要对有限元模型进行模型修正。

表3 试验模态结果与有限元模态结果的对比Tab.3 Comparison of experimental modal results with finite element modal results

3 对接圆柱壳结构的有限元模型修正

对接圆柱壳结构的有限元模型修正流程如图6所示。其具体流程包括参数筛选、试验设计、响应面模型构造、响应面拟合精度分析、模型修正及结果分析5部分。具体地，选择合适的设计参数；根据数理统计方法在参数的设计空间内确立样本点；由样本点计算响应值获得完整的样本数据；由样本数据选择合适的响应面模型；依据实测试验数据确定合适的目标函数,根据响应面模型进行迭代修正，最后获得修正后的有限元模型并进行修正精度分析。

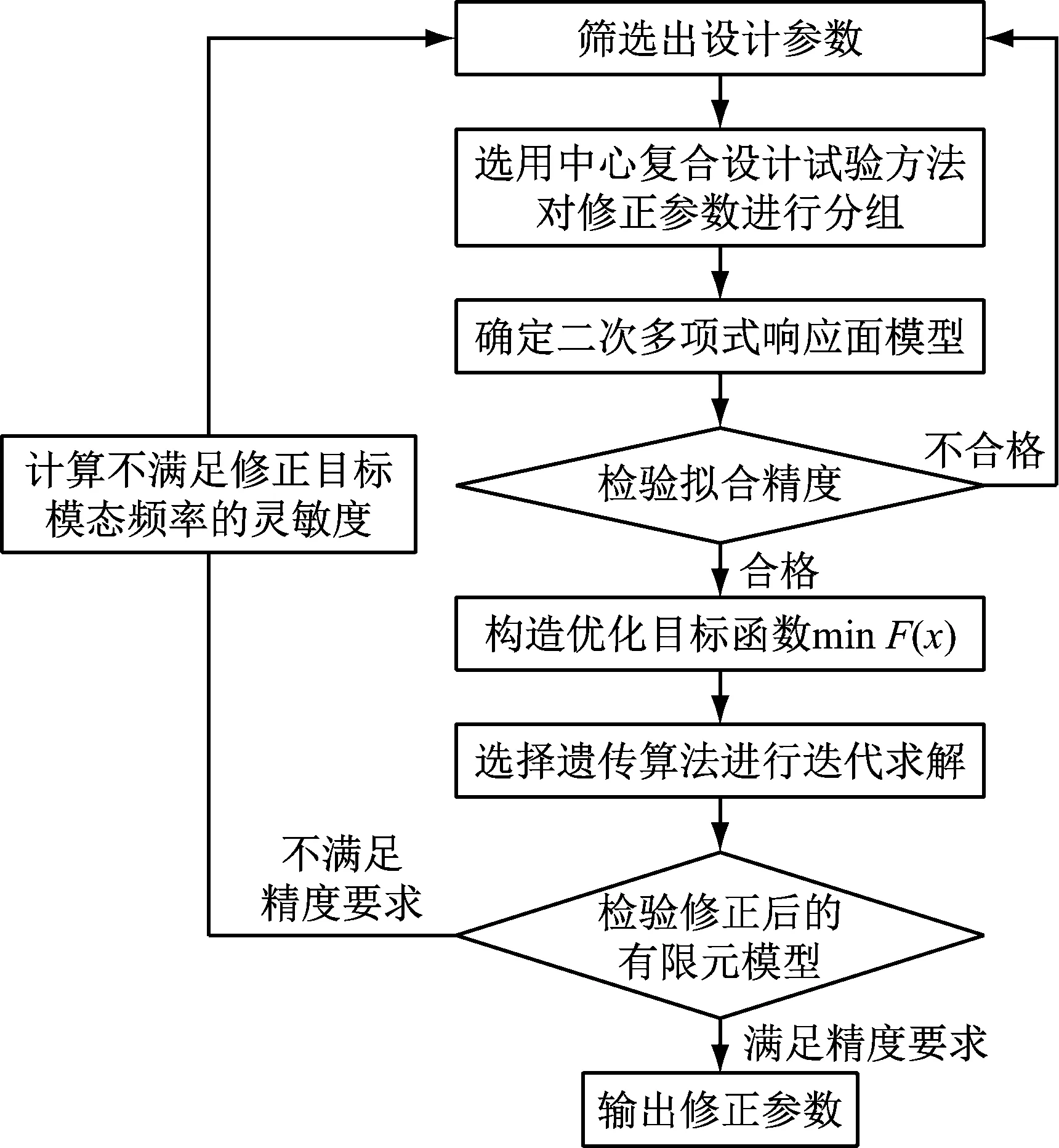
图6 对接圆柱壳结构的模型修正流程图Fig.6 Model updating flow chart of butted cylindrical shell structure

3.1 参数筛选和试验设计

由于单个圆柱壳结构由法兰和圆柱壳两部分焊接构成，而对接圆柱壳结构的圆柱壳部分采用同种材料锻造而成。根据工程经验，选择弹性模量、密度和泊松比作为待修正参数，对其进行上下10%的取值。随后采用三因素、五水平的中心复合设计试验方法[21]，三个因素的水平数如表4所示。选取的15组设计方案如表5所示，根据不同方案更新有限元模型，并分别计算模态频率，获得完整的样本数据。

表4 设计变量因素水平表Tab.4 Design variable factor level table

表5 中心复合设计试验表Tab.5 Central composite design test table

3.2 响应面模型构造

目前，二次多项式[22]、BP神经网络[23]、高斯径向基函数[24]、Kriging模型[25]和支持向量机是比较常见的响应面模型。本文采用常用的不考虑交叉项的二次多项式响应面[26]。其响应面模型可表示为

(2)

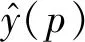
(3)

式中，k为试验次数。

A=[a,b,c]T，

a为单量，b=[b1,b2,…,bn]，c=[c1,c2,…,cn]。

当k>2n+1时，则PTP非奇异，由最小二乘法可得响应面模型的系数

A=(PTP)-1PTY

(4)

得到模型系数之后，进而可得到二次多项式响应面模型。

3.3 响应面拟合精度分析

在响应面模型建立之后，需要评价响应面函数与有限元结果之间的拟合程度和响应面模型的有效性。常用的评价因子有决定系数R2和均方根误差ERMS(root mean square error,RMSE)两种检验标准[27]。

(5)

(6)

对拟合后的响应面模型进行拟合精度分析，表6给出了对应的决定系数和均方根误差。结果显示各阶模态频率的决定系数均为1，均方根误差值则在10-6数量级，这表明响应面模型与有限元模型的差异很小，响应面模型的精度符合要求，可代替有限元模型进行后续的修正计算。

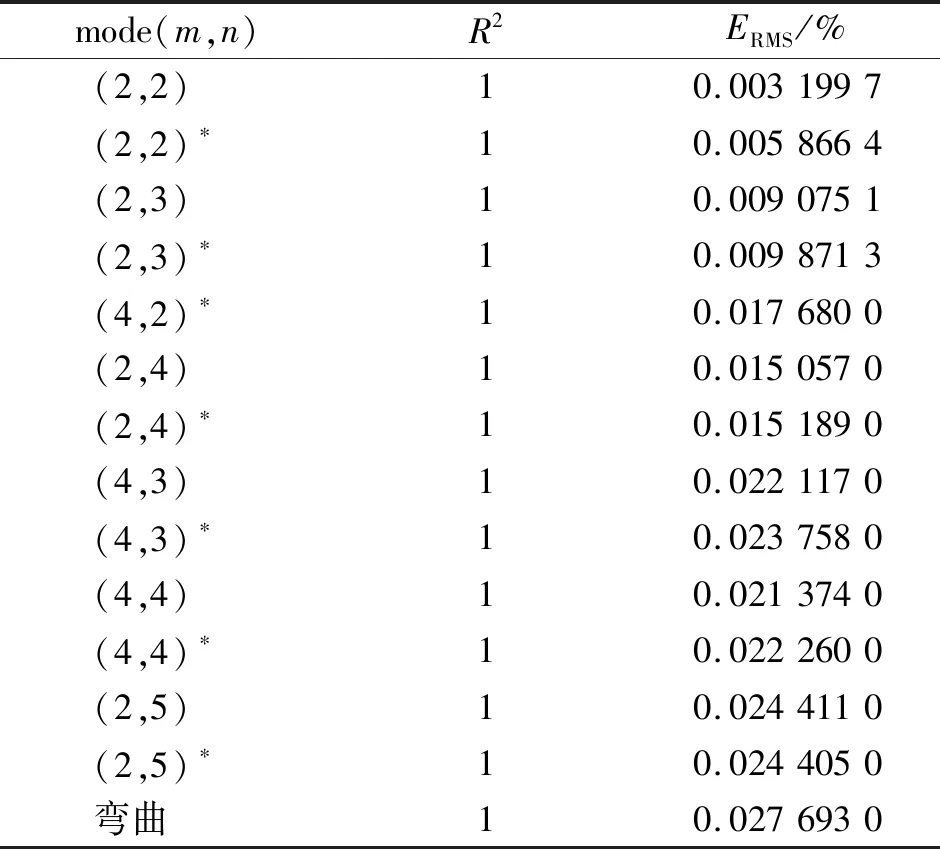
表6 模态频率决定系数和均方根误差Tab.6 Determination coefficient and root mean square error of modal frequencies

3.4 模型修正及结果分析

在得到满足精度要求的响应面模型之后，将根据响应面模型和试验的目标响应值构造目标函数，选择优化算法进行优化求解。本文选择多目标遗传算法[28]，该算法是非支配排序遗传算法的一种变体。它支持多个目标和约束，旨在找到全局最优值[29]。以响应面模型和试验结果的各阶模态频率相差最小作为目标函数[30]，目标函数可以表示为

(7)

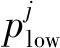
图7给出了修正前后的有限元模型计算得到的模态频率与试验模态频率的相对变化率，其中样本点为200，最佳修正密度为2 659.6 kg/m3，最佳修正弹性模量为70.627 GPa，最佳修正泊松比为0.305 22。从图7中结果可以看出,修正后的有限元模型得到的各阶模态频率与试验结果相比总体有所减小，但第7阶模态频率与试验值的相对误差仍大于5%。第5阶、第6阶模态频率与试验值的相对误差接近5%。这说明需要在现有修正基础上进行二次模型修正。

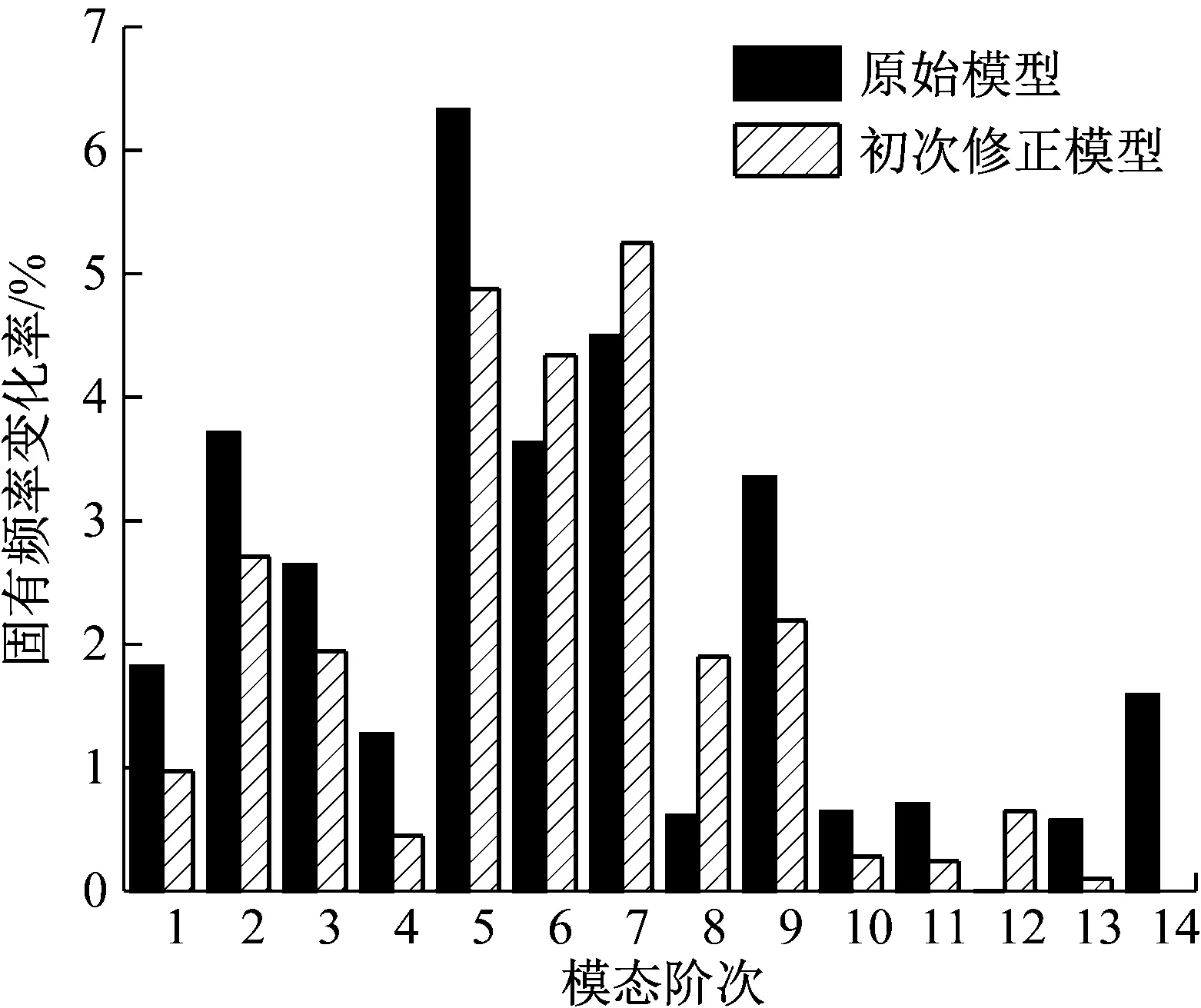
图7 初次模型修正前后的模态频率变化率Fig.7 Change rate of modal frequency before and after the first model updating

在上述响应面模型修正的基础上，分析第5阶、第6阶、第7阶模态频率对设计参数的灵敏度。图8给出了初次修正后第5、6、7三阶模态频率对设计参数的灵敏度情况。从图8中结果可以看出，这三阶模态频率对泊松比最灵敏，密度和弹性模量的影响较小可以忽略不计。

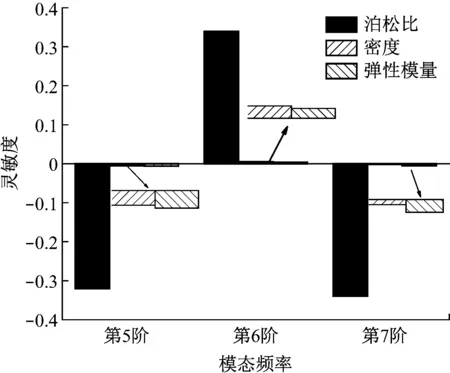
图8 初次修正后第5、6、7阶模态频率对设计参数的灵敏度Fig.8 The sensitivity of the 5th,6th and 7th modes frequencies to design parameters after the first model updating

表7给出了模型修正前后的模态频率相对误差情况，其中样本点为200，最佳修正泊松比为0.263 77。表7中还给出了灵敏度分析方法的结果。从表7中结果可以得出：(1)与修正前的误差相比，响应面法得到的各阶模态频率最大误差由6.33%变为4.63%，其相对误差均在5%以内，已满足工程实际的计算需求。(2)与修正前的误差相比，灵敏度分析方法得到的各阶模态频率最大误差由6.33%变为5.50%，误差有所下降，但不符合工程实际计算要求。(3)灵敏度分析方法得到的各阶模态频率最大相对误差为5.50%，响应面法得到的最大相对误差为4.63%。两种方法相比，响应面法的修正效果更明显，精度要更高，进一步验证了响应面法的有效性。此外，灵敏度分析方法实际上是基于有限元软件的不断迭代，直至达到精度要求，对于复杂化的模型多次调用有限元计算会使计算效率大大降低。响应面法通过建立一个代理模型替代有限元模型，在计算效率方面具有明显的优越性。

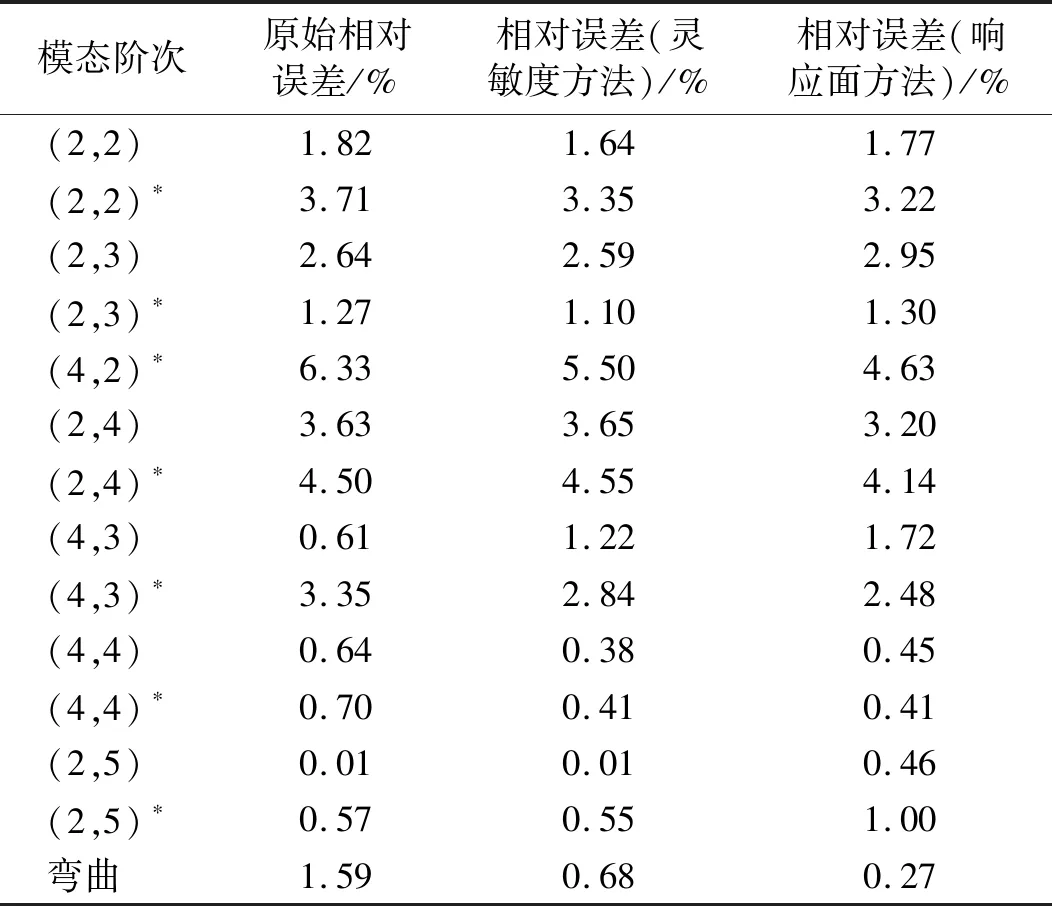
表7 模型修正前后的模态频率相对误差Tab.7 Relative error of modal frequency before and after model updating

图9给出了模型修正前后的模态频率相关性分析结果。将试验模态频率和有限元修正后的模态频率分别作为直角坐标系的横纵坐标，如果各阶频率值在对角线附近，说明各阶模态频率对应的比较好。从图9中结果可以看出,计算的各阶模态频率与试验值接近，说明了响应面法的有效性。图10给出了重点修正的模态频率对应的模态振型，也给出了试验模态振型结果。由图10可知,修正后的有限元模型计算结果与试验振型具有较好地一致性，进一步说明采用响应面法对对接圆柱壳结构进行有限元模型修正具有较高精度。

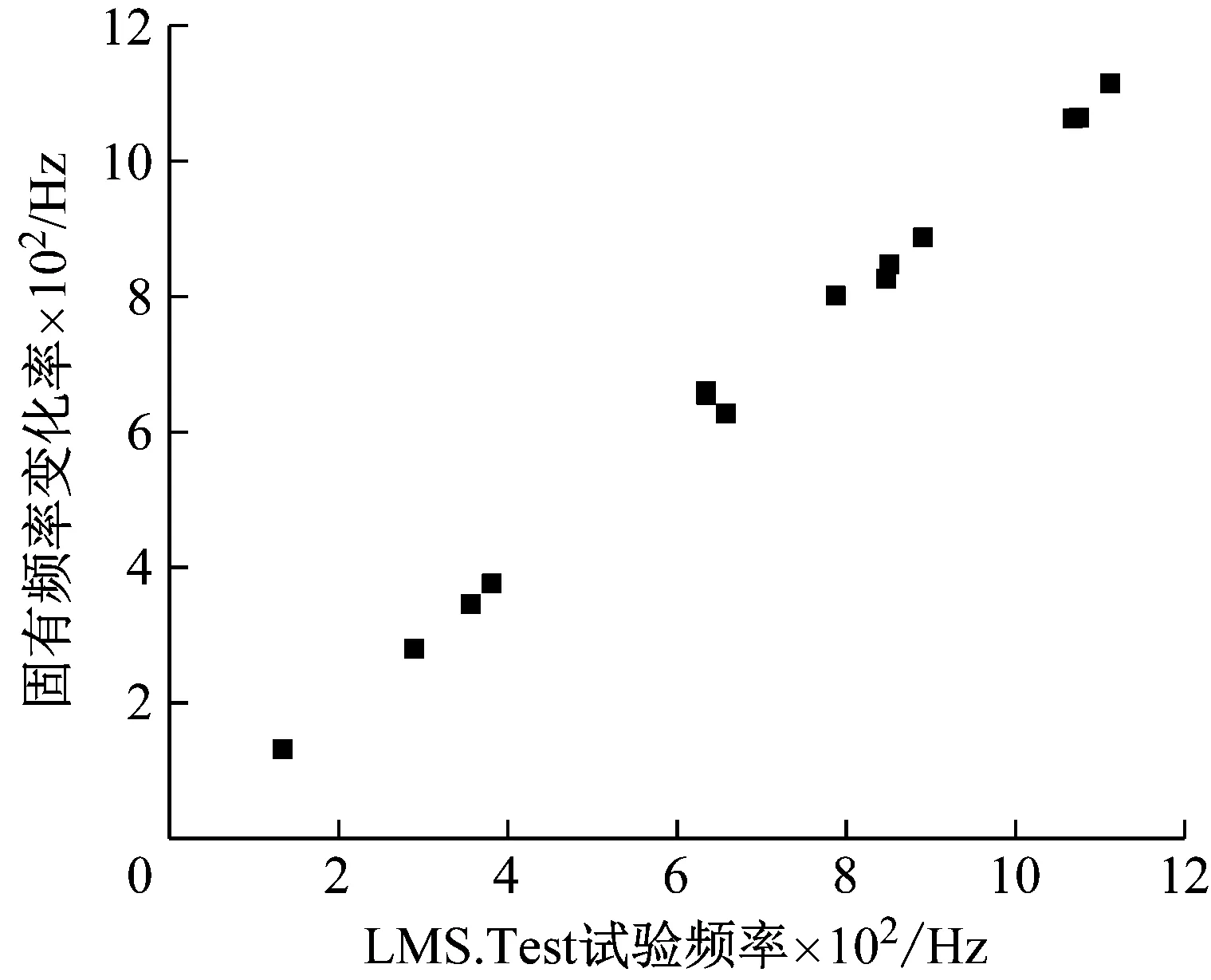
图9 模型修正前后的模态频率相关性分析Fig.9 Modal frequency correlation analysis before and after model updating

(a) 试验模态振型(4,2)*

4 结 论

本文以对接圆柱壳结构为研究对象，采用LMS数据采集分析系统进行了结构的模态试验，另一方面利用ANSYS有限元软件建立结构的有限元模型并进行模态分析，对比模态试验结果和有限元仿真结果以确定有限元模型的准确性。根据模态试验得到的模态频率与响应面计算结果之差构造修正目标函数，选择待修正参数并采用多目标遗传算法对对接圆柱壳结构有限元模型进行了优化修正，并利用模态试验数据对修正后的有限元模型进行验证。根据模态试验与有限元模型修正的结果，可得以下结论：

(1) 通过对对接圆柱壳结构自由边界条件下的模态试验结果进行分析，得到了对接圆柱壳的振型特点。对于周向节点数相同的模态，模态频率有多组。此外，周向的半波数和轴向波数随着模态阶数的增加而增加，表现出圆柱壳结构的一般振动特性。但由于结构为对接形式，振型呈现出以法兰面为分界的对称振动和非对称振动。

(2) 采用响应面法修正后得到的有限元模态频率与实测模态频率间相对误差明显减小，具体地，与修正前的误差相比，响应面法得到的各阶模态频率最大误差由6.33%变为4.63%，其相对误差均在5%以内，已满足工程实际的计算需求。结果表明,采用响应面法进行模型修正有效提高了对接圆柱壳有限元模型的准确度，取得更好的预测效果，进而验证了基于响应面法在对接圆柱壳有限元模型修正中的有效性。

(3) 灵敏度分析方法得到的各阶模态频率最大相对误差为5.50%，响应面法得到的最大相对误差为4.63%。两种方法相比，响应面法的修正效果更明显。此外，灵敏度分析方法实际上是基于有限元软件的不断迭代，直至达到精度要求，对于复杂化的模型多次调用有限元计算会使计算效率大大降低。响应面法通过建立一个代理模型替代有限元模型，在计算效率方面具有明显的优越性。