基础激励下磁悬浮转子系统动力学建模与分析

2022-09-23马彦超徐园平

振动与冲击 2022年17期

沈权，周瑾，马彦超，徐园平，张越

(南京航空航天大学机电学院，南京 210016)

近年来随着磁悬浮技术的发展，磁悬浮轴承逐渐被广泛应用于车载飞轮，航天控制力矩陀螺，船用涡轮机等旋转机械设备中[1-3]。尽管许多国内外学者已经从各个方面开展了以主动磁悬浮轴承(AMB)支承的转子系统的动力学特性研究，但基本集中在静止基础条件下[4-6]，基础激励下磁悬浮转子系统的相关研究还不够充分。当转子安装在船舶，车辆，飞机等基础发生运动的设备上时[7-8]，与基础固连的轴承定子运动所引起的基础激励会影响磁悬浮转子正常工作。这个问题可以归结为基础激励下的磁悬浮转子振动问题，因此建立基础激励下磁悬浮转子的动力学模型，分析转子系统的动力学特性有着重要意义。

Duchemin等[9-10]考虑传统轴承支承(例如滚动轴承，滑动轴承)的柔性转子，基于拉格朗日方程建立了基础激励下转子运动方程；Das等[11-12]基于机动车辆上的转子进行拉格朗日建模，将磁悬浮轴承作为作动器，用于抑制转子振动，得到了基础简谐激励下的转子运动方程，但方程未考虑重力变化与转动引起的附加力矩影响。蒋科坚等[13-14]首先推导了基础激励下单自由度磁悬浮轴承支承模型，进一步推广到多自由度转子模型，研究表明不考虑陀螺效应，基础正弦激励可以等效为转子受到一个由基础加速度决定的强迫振动，但转子模型未考虑基础转动的影响。Li等[15]基于航天器中磁悬浮控制力矩陀螺，利用欧拉动力学等力学理论建立了双框架运动下的转子运动方程，然而框架顺序影响着转子受到的耦合力矩，并且转子陀螺效应明显，并不适用于一般转子。

在动力学分析方面，Zheng等[16]基于基础激励下的磁悬浮转子数学模型，在模型稳定性分析基础上，从转子渐近稳定性和区域稳定性两方面进行了讨论。Soni[17]利用线性时变系统的稳定性分析方法，通过转子数学模型的状态矩阵，求解近似状态转移矩阵进行稳定性分析，得到了不同基础激励参数下的转子稳定区间。Xu等[18]在建模中考虑了基础平动与基础转动，探究了系统与激励各参数对磁悬浮转子位移幅值的变化规律。姜豪等[19]讨论了应用在船舶设备中不同基础倾斜工况下的磁悬浮转子动力学特性，通过仿真和试验得出基础倾斜工况不仅会使转子响应出现倍频成分，基础倾斜引起的重力变化也不可忽略。杨红进等[20]以车载飞轮为研究对象，并不基于转子数学模型，而是利用ADAMS与Simulink进行基础激励下磁悬浮转子的联合仿真，分析了车辆加减速、转弯、爬坡、路面颠簸引起的横向，俯仰等工况下转子的振动位移响应，并简要分析了不同基础激励下转子的运动状态。

通过对各学者研究工作的介绍，还存在以下问题需要深入探究：(1)部分磁悬浮转子建模只考虑了基础平动激励，未考虑基础转动影响；(2)尽管部分研究通过拉格朗日方程建模考虑了基础转动影响，但未考虑基础转动引起的重力变化与附加耦合力矩影响，同时并未辨明磁悬浮轴承支承力在方程中的关系；(3)在稳定性分析中未考虑磁悬浮轴承电磁力变化的影响；(4)动力学分析中并未深入研究转速，附加偏心等参数变化以及基础激励参数之间对转子振动产生的耦合影响。

基础激励也是十分复杂的，从分类上讲，基础激励可以分为平动激励与转动激励；与转子作用方向相结合，也可以分为径向激励和轴向激励。不同的基础激励作用形式也不相同，例如简谐激励、冲击激励、随机激励等，简谐激励主要由频率与振动幅值决定，冲击激励主要由冲击脉宽与冲击幅值决定，而随机激励主要由功率谱密度决定等等。

针对上述问题，选取在船舶车辆中常见的基础简谐激励，首先考虑不平衡、重力、非定点转动的附加惯性力矩影响，建立了基础激励下磁悬浮转子的动力学模型；搭建了磁悬浮转子系统机电一体化模型；然后利用等效刚度阻尼模型分析了各参数对磁悬浮转子系统的稳定性的影响；最后从转子轨迹，振动幅值两方面分析了不同基础激励参数对磁悬浮转子的影响。

1 基础激励下磁悬浮转子动力学建模

在进行转子动力学建模之前，首先需要明确传统轴承支承的转子建模与磁悬浮轴承支承的转子建模在原理上是相似的，只是对轴承支承力处理方法不同。

1.1 磁悬浮转子动力学分析

一般转子运动方程有两种建模方法，一种是利用牛顿力学与欧拉动力学方程等力学理论，另一种则采用拉格朗日方程。两者在结论上是等价的，但第二种方法逻辑简单直接，较为常用，因此本文将采取拉格朗日方程进行转子建模。

无论基础是否运动，利用拉格朗日方程建模的思路是不变的。首先确立转子及其相关坐标系，然后求解转子动能，势能，耗散能以及广义力，最后代入方程求解计算，拉格朗日方程的一般形式如下：

(1)

式中：T为系统的动能；R为系统的耗散能；V为系统的势能；x为广义坐标；Q为系统受到的各种广义力。

磁悬浮轴承支承力在拉格朗日方程中的应用与传统轴承不同，磁悬浮轴承电磁力一般做广义力处理，而不作为刚度阻尼项施加到转子运动方程中。由于电磁力的支承特点，支承刚度引起的势能与支承阻尼所引起的耗散能由广义力代替，故只分析转子动能即可。

径向磁轴承采用8极差动结构，由于磁悬浮转子径向与轴向耦合很小，所以只需求解径向四自由度磁悬浮转子运动方程，轴向可以按照单自由度磁悬浮转子建模。

1.2 转子及相关坐标系

正如1.1节中的转子建模思路，建立以下坐标系：

参考坐标系Oxyz：大地为参考的笛卡尔坐标系。

基础坐标系Obxbybzb：固连于设备基础上的坐标系，各坐标轴与参考坐标系平行，z轴为设备前进方向，基础相对大地运动的位置向量为[ubx,uby,ubz,θbx,θby,θbz]。

转子坐标系Orxryrzr：固连于转子质心的坐标系(简称b系)，初始时基础系原点与转子系原点重合，为了提高转子承载能力，磁悬浮轴承径向布置偏转45°，转子系相对基础系的位置关系如图1、2所示，转子相对基础运动的位置向量为[ux,uy,uz,θx,θy,θz]。

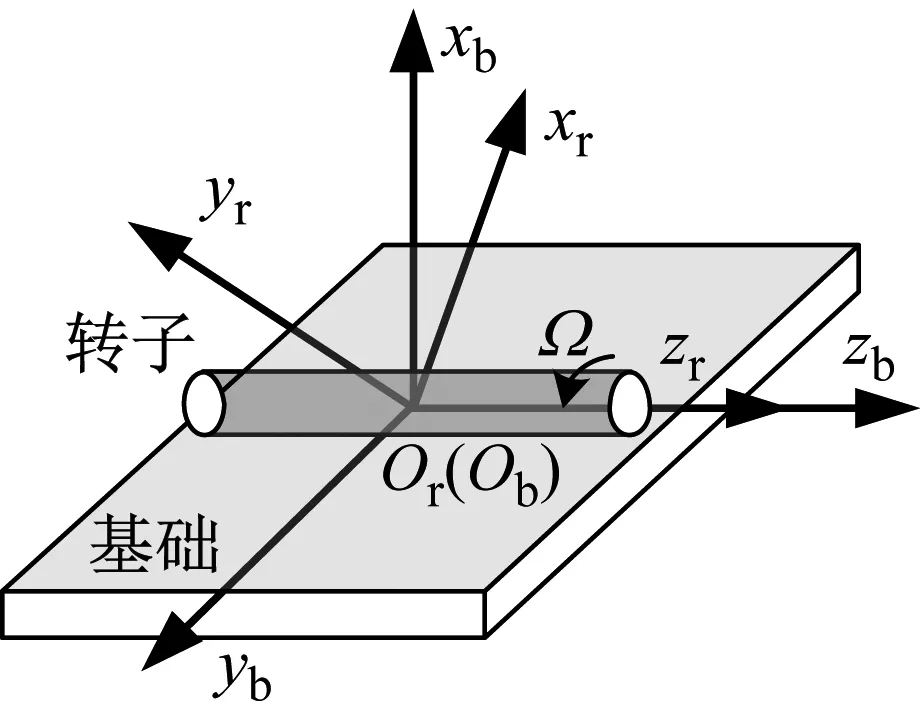
图1 转子与基础的位置关系Fig.1 Position relationship between rotor and foundation

图2 转子系相对基础系在z方向夹角关系Fig.2 Angle relationship between rotor system and foundation system in z direction

虚拟基础坐标系Obxgygzg：为了便于分析，定义固连于基础上的虚拟系(简称g系)，g系为b系绕z轴顺时针旋转45°得到，应用虚拟基础系后，即与最终转子坐标方向保持一致。虚拟基础对应的位置向量为[ugx,ugy,ugz,θgx,θgy,θgz]，而虚拟基础位置向量与基础位置向量变换关系为

(2)

则g系到b系的变换矩阵为

(3)

1.3 转子动能与动力学方程

转子动能有平动动能与转动动能两部分组成，对于转子的平动动能，基础g系相对大地参考系的位置向量为rg=[ugx,ugy,ugz]，转子质心在基础g系下的位置向量为ri=[ux,uy,uz]。

则转子速度向量表示为

(4)

这里ωg×ri为叉乘，其中ωg为坐标系耦合矩阵，表示为

(5)

则转子平动动能为

(6)

在转子的转动动能求解中，转子的角速度需要用欧拉角表示，在这里选取常应用于航空航天领域的克雷洛夫角(也称卡尔丹角)。

转子角速度向量为

(7)

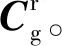
(8)

(9)

式中，α，β，γ为惯用表达，α=θx，β=θy，γ=θz。以ωr为例，欧拉角转动关系如图3所示

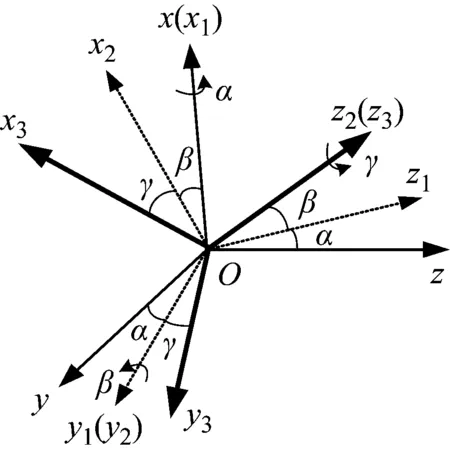
图3 欧拉角转动次序关系Fig.3 Euler angle rotation order relation

(10)

则转子转动动能为

(11)

将转子动能代入拉格朗日方程中，取转子质心q=[ux,uy,θx,θy]作为广义坐标，以基础g系为参考，经公式推导及简化处理后得到转子径向四自由度动力学方程

(12)

式中，q=[x,y,α,β]=[ux,uy,θx,θy]。q表示质心处转子的位移，f=[fx1,fx2,fx3,fx4]T表示磁悬浮轴承提供的电磁力，M为广义质量矩阵，G为陀螺矩阵，B为电磁力作用矩阵，Fg为基础振动所产生的等效广义力向量，具体简化及矩阵形式详见附录A。

1.4 附加惯性力矩与重力扰动建模

转子转动动能建模过程中，大部分学者都忽略了非定点转动对转子产生附加力矩的影响。实际上基础并非围绕基础系原点定点转动，结合刚体动量矩定理[21]，附加惯性力矩实质上表现为转子的附加刚度矩阵Kg以及广义力矩阵Fg，具体形式见附录B。

同样地，学者们也忽略了基础运动引起的重力扰动的影响。实际上基础平动不会产生重力扰动，基础转动的两个自由度会产生重力扰动影响，基础转动下重力载荷变化如图4所示

(a) z向转动

重力扰动实质上影响径向x、y方向磁悬浮轴承的承载平衡，通过简单推导，重力扰动FG表示为

(13)

1.5 转子不平衡建模

转子由于制造或安装误差等，质量不平衡是必然存在的，但这并不影响基础振动建模，所以转子不平衡可以单独建模。

假设不平衡质量点为qg，则质量不平衡可以表示为

(14)

式中:e和φ表示静不平衡的的幅度和相位；ε和γ表示动不平衡的的幅度和相位。推导得到由于转子不平衡等效的惯性力矢量为

(15)

由于本文中磁悬浮转子轴向长度要远大于径向长度，故Jz忽略不计。不平衡力简化为

(16)

1.6 转子运动方程

综合考虑了附加惯性力矩，重力扰动以及不平衡力之后，代入基础b系到虚拟g系的坐标变换Cgb，最终基础激励下转子动力学方程为

(17)

其具体矩阵形式详见附录C。

通过上述方程可以看到，基础激励下的磁悬浮转子除了受到电磁力、不平衡力、重力扰动作用之外，还受到基础激励引起的广义外力作用，同时还产生了附加刚度和阻尼矩阵。

由于转子运动方程的复杂性，为了便于后续仿真研究，这里对方程各参数进行分析和简化处理。方程的运动参数主要由转子运动参数和基础运动参数组成，本文主要分析径向四自由度下转子动力学行为，由于轴向磁悬浮轴承位移很小，忽略转子轴向位移uz的影响，即对Fb简化处理，矩阵详见附录D。

基础运动参数主要有径向平动激励(以位移参数表示为ux,uy)、径向转动激励(θx,θy)、轴向平动激励(uz)、轴向转动激励(θz)，径向基础激励在x和y方向自由度上作用是等价的，因此仿真主要讨论ux，θy，uz，θz以及它们的复合运动，从激励频率与幅值两个方面分析转子的影响规律。

2 磁悬浮转子系统机电一体化建模

2.1 磁悬浮转子系统模型

磁悬浮转子系统作为典型的闭环反馈系统，主要由五部分组成，分别是转子、磁悬浮轴承、控制器、功率放大器、传感器。本文所使用的磁悬浮轴承参数见表1；转子结构图如图5所示，参数见表2。

表1 磁悬浮轴承主要参数Tab.1 Main parameters of magnetic bearing

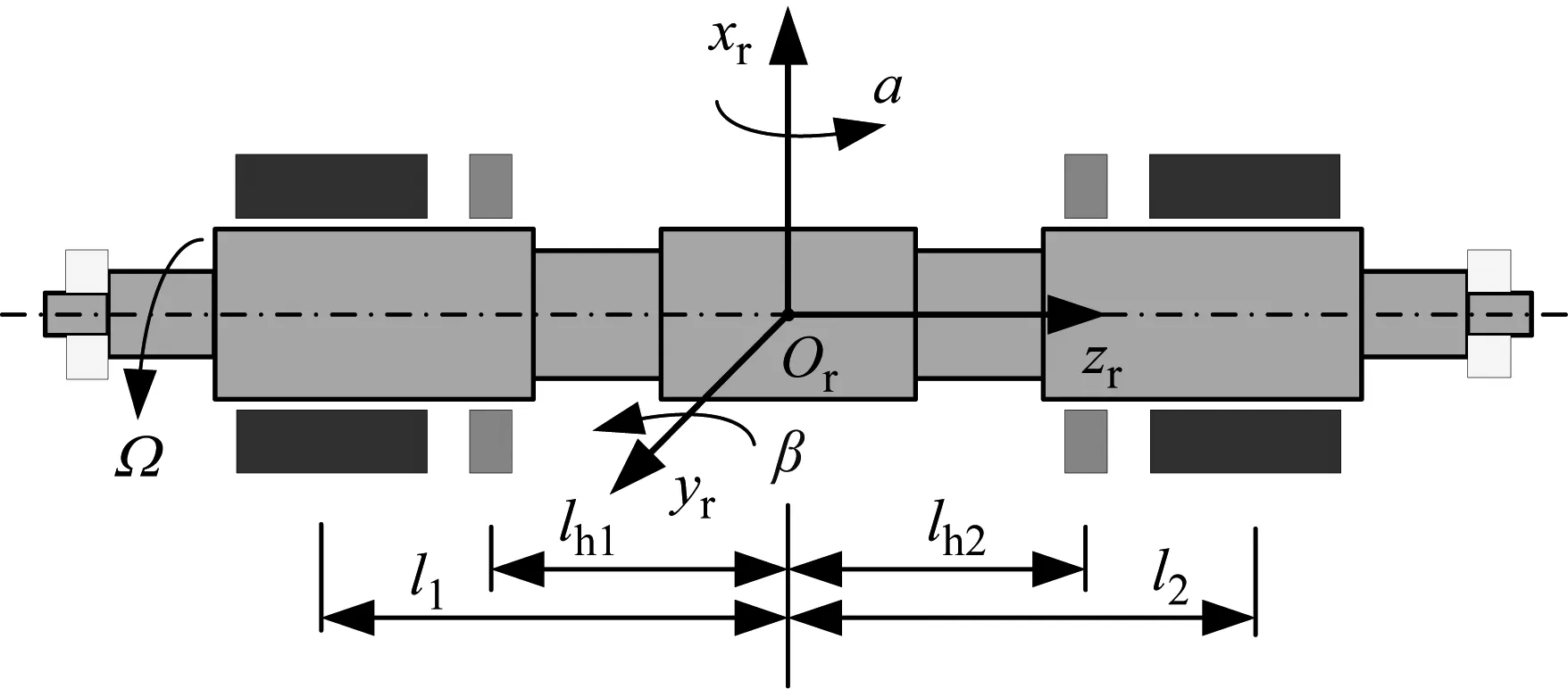
图5 磁悬浮转子结构尺寸Fig.5 Structural dimensions of magnetic levitation rotor

表2 转子结构各参数尺寸Tab.2 Parameters and dimensions of rotor structure

在磁悬浮转子系统中，传感器为实际测量转子变化量的部件，转子输出的径向位移需要通过控制器输出控制电流在磁悬浮轴承处进行控制，然而传感器、控制器、磁悬浮轴承作用点并不在同一位置。为描述转子受基础激励的响应特性，转子位移统一表示为传感器处转子的位移。令磁轴承处转子位移为qd=[x1,y1,x2,y2]T，传感器处的转子位移表示为qh=[xh1,yh1,xh2,yh2]T，则质心位移q与qd，qh之间转换矩阵为

qc=Rqd,qc=Hqh

(18)

为了建立磁悬浮转子机电一体化模型，应从电磁力入手，因为系统各部分最终体现于磁悬浮轴承的电磁力中，电磁力与转子位移q有着密切的关系，实际磁悬浮轴承产生的为非线性电磁力，一般磁悬浮轴承在线性工作区[22]，线性化后电磁力为

f=KiI-Kxqd

(19)

式中，Ki=diag[kix1,kiy1,kix2,kiy2]T为各个磁轴承的力-电流刚度组成的矩阵，Kx=diag[kxx1,kxy1,kxx2,kxy2]T为各个磁悬浮轴承的力-位移刚度组成的矩阵，I=[ix1,iy1,ix2,iy2]T为磁轴承的控制电流组成的向量。

电磁力主要由控制电流决定，其包含了闭环控制系统各个环节的作用，本文采用的位移传感器和功率放大器均可以视为理想的比例环节，控制器采用经典的PID控制，其传递函数为

(20)

式中，kP为控制器比例系数，kI为控制器积分系数，kD为控制器微分系数。

则控制电流在时域下表达为

(21)

式中，ka为功放增益系数，ks为传感器增益系数，ka和ks均为常数。

2.2 等效刚度阻尼与状态空间模型

将电流表达式代入到转子运动方程的电磁力中，可以看到方程既有二阶微分项同时也存在积分环节，为了便于稳定性分析以及探究控制系统各环节对系统的影响，建立电磁力等效刚度阻尼的概念，利用频域变换求解磁悬浮轴承的等效刚度阻尼，建立完善的状态空间模型。

利用推导的转子动力学方程，转子坐标统一用广义坐标系q(即质心坐标系)表示，将控制电流项代入，转化到频域得

s2Mqc+s(G+Cb)qc+(BKiGsGcGaH-1+

BKxR-1+Kb)qc=Fu+Fb+Fg

(22)

根据电磁力等效支承力

(23)

代入转子运动方程(17)中可得

Fu+Fb+Fg

(24)

转化到频域得

s2Mqc+s(G+Cb+BCR-1)qc+(Kb+BKR-1)qc=

Fu+Fb+Fg

(25)

然后令s=jω代入得

[(-Mω2+Re(BKiGsGaGc)H-1+BKxR-1+Kb)+

j(Gω+Cbω+lm(BKiGsGaGc)H-1)]qc=

Fu+Fb+Fg

(26)

[(-Mω2+BKR-1+Kb)+j(Gω+Cbω+

BωCR-1)]qc=Fu+Fb+Fg

(27)

由此可得等效刚度阻尼为

(28)

令

CB=G+Cb+BCR-1

KB=Kb+BKR-1

FB=Fu+Fb+Fg

(29)

则转子状态空间模型表示为

(30)

3 系统稳定性分析

3.1 稳定性分析理论

稳定性分析的方法有很多，如传统控制理论进行分析(例如利用劳斯判据，奈奎斯特判据，bode判据等)，也有现代控制理论的分析(利用李雅普诺夫稳定性理论)，也有利用近似求解模型的状态转移矩阵的特征值来判别稳定性[23]，本文研究的磁悬浮刚性转子系统实际上是一个二阶系统，在经过电磁力线性化之后，磁悬浮转子的动力学方程为二阶线性微分方程，只需要考虑齐次方程。

结合转子系统的状态空间模型，根据特征方程判断特征值来进行稳定性的分析。

由现代控制理论可知，对形如

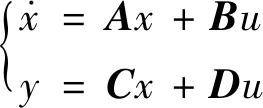
(31)

上述状态空间模型，其传递函数形式为(一般D阵为零阵)

(32)

即系统特征方程为det(sI-A)=0，当其特征根实部为负值，则证明系统是稳定的。

需要注意的是矩阵A中的陀螺矩阵项以及等效刚度阻尼项均与转速相关，不同转速下对应的特征值并不相同，不同转速对系统稳定性的影响并不是本文的研究重点，而是重点研究基础运动参数以及闭环系统控制器参数对于系统稳定性的影响。在仿真计算中为使PID控制器稳定，引入不完全微分Tf，系统电控模型相关参数如表3，各参数表达详见2.1节。

表3 系统电控模型参数Tab.3 System electric control model parameters

转子转速取固定转速ω=50 Hz，通过等效刚度阻尼模型计算，该转速下径向磁悬浮轴承等效刚度约为5.6×105N/m，等效阻尼约为525.6 N·s/m。

3.2 基础激励参数对系统稳定性影响

通过特征方程可知，影响转子稳定性的参数主要有两部分，一部分为基础运动参数，一部分为转子系统参数，例如控制参数，偏置电流等。

表4 不同基础激励的稳定性仿真参数Tab.4 Stability simulation parameters of different foundation excitation

图6(a)为x方向基础平动频率变化对转子系统稳定性的影响，特征根固定于复平面的某一位置，振动频率的变化并没有导致特征根发生偏移，从图中可以看出虽然振动频率很高(工况中难以达到)，特征根仍然居于负半平面，系统是稳定的。

图6(b)为y方向基础转动频率变化对转子系统稳定性的影响，可以看出随着振动频率的升高，一组特征根趋近并越过虚轴进入正半平面，临界振动频率约为340 Hz，即y向基础转动达到该频率以上，系统发生失稳。

图6(c)为z方向基础平动频率变化对转子系统稳定性的影响，虽然随着基础振动频率的升高，特征根发生了轨迹偏移，但和图6(a)类似，特征根仍然居于负半平面，系统是稳定的。

(a) x方向基础平动根轨迹

图6(d)为z方向基础转动频率变化对转子系统稳定性的影响，可以看出与其他基础激励不同，由于z向转动二次项的影响，特征根的轨迹更加复杂，随着振动频率的增加，两组特征根趋近并越过虚轴进入正半平面，通过计算在120 Hz左右系统开始在正半平面出现了特征根，系统失稳。

上述分析讨论了基础激励单参数对系统稳定性影响，当考虑存在多个基础激励参数变化时，经过计算分析并验证，系统特征根轨迹主要由影响较大的基础激励参数决定，其余激励参数的增大只会进一步加快轨迹点向正半平面移动。同时，从激励方式来看，基础振动幅值变化与振动频率在稳定性分析上是等价的，因此不必再分析基础振动幅值变化对转子系统稳定性的影响。

综合来看，不论是径向还是轴向，基础平动变化不会引起转子系统的失稳，基础转动在一定参数下会使系统发散，但需要注意的是，本节稳定性分析并未考虑外力矢量与电子器件饱和的限制，往往当基础激励还未到达失稳的基础频率或振动幅值，系统因外力过载和器件限幅就已失稳，在工程应用中应综合考虑外部条件的限制。

3.3 系统参数对系统稳定性影响

本节讨论系统参数对系统稳定性影响，功率放大器与位移传感器参数在转子系统中默认为常值，由此主要讨论控制参数kP，kI，kD与偏置电流i0对转子系统稳定性的影响，为了控制变量，给定初始基础激励为分别为x向平动与y向转动的固定参数。图7分别为kP，kI，kD，i0四种系统参数变化的特征根轨迹，仿真参数如表5所示。

表5 控制仿真参数与偏置电流仿真参数Tab.5 Control simulation parameters and bias current simulation parameters

图7(a)为比例系数对转子系统稳定性的影响，在一定的基础激励下，当kP小于0.8时，存在特征根位于正半平面，系统是失稳的；随着参数增大，位于正半平面的特征根轨迹向负半平面移动，系统趋于稳定，这与PID控制特性是一致的，当kP较小时，导致转子系统刚度不足，系统发生失稳。

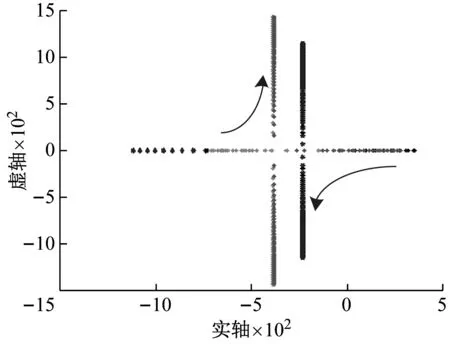
(a) 比例系数kP特征根轨迹

图7(b)为积分系数对转子系统稳定性的影响，从图中可以看出，随着参数kI增大，根轨迹虽然向正半平面发生偏移，但整体处负半平面，可见积分系数对系统稳定性的影响并不大，这也和PID特性是一致的。

图7(c)为微分系数对转子系统稳定性的影响，从图中可以看出，在微分系数取零时，特征根正好位于虚轴上，系统处于临界稳定；随着微分系数的增大，特征根轨迹向负半平面移动。关于系统临界稳定的原因是虽然微分系数为零，但系统仍具备刚度支承力，实际上转子没有阻尼会发生剧烈震荡，工程实践中临界稳定也是不可取的。

图7(d)为偏置电流对转子系统稳定性的影响，从表4偏置电流仿真参数可以看出，电流不能为零，这是由于偏置电流要支承转子重力载荷。从图中可以看出在偏置电流参数范围内，特征根始终位于负半平面，系统是稳定的；随着偏置电流参数的增大，根轨迹逐渐向负半平面移动，但偏置电流也不宜过大。

整体来看，控制参数对转子系统稳定性影响可以从PID控制特性来分析，比例系数主要影响支承刚度，微分系数主要影响支承阻尼，kP过小，系统刚度不足发生失稳，kD过小，系统阻尼不足会引起振荡。而积分系数对系统稳定性影响很小，偏置电流实质上决定着轴承支承力大小，偏置电流不宜过小否则不足以支撑转子重力，同时也不宜过大否则导致电子器件饱和。

3.2、3.3节讨论了基础激励参数，系统参数对转子稳定性的影响，确定参数范围，可以为后续控制设计提供指导。

4 基础激励仿真研究

上一节主要讨论了各参数对转子系统稳定性的影响，本节重点研究转子系统的位移响应特性，分别从转子轨迹与振动位移幅值两个方面探究基础激励参数对转子位移响应的变化规律。

4.1 基础激励对转子轨迹影响

与第3节分析类似，虽然转子系统模型参数众多，较为复杂。但径向各基础激励参数具有类比性，故只研究一半参数即可，从变量个数上讲，分别是x向平动，y向转动，z向平动，z向转动以及它们的复合运动，转子位移取1，2路位移参考信号。

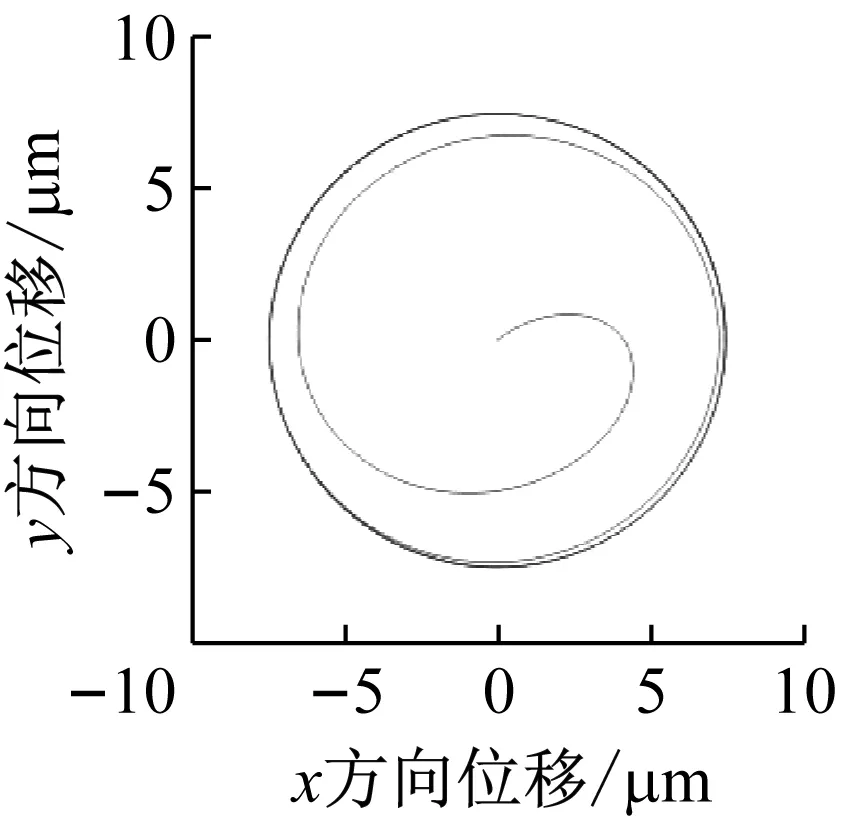
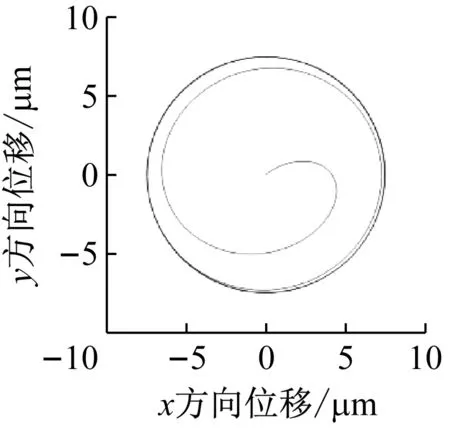
为了方便对比分析，以固有不平衡作为转子位移轨迹参考，仿真时间取2 s，静偏心取5×10-6m，转子转速为100 Hz，该转速下径向磁悬浮轴承等效刚度约为5.45×105N/m，等效阻尼约为524.4 N·s/m。磁悬浮转子仿真如图8、9所示。

(a) 无基础激励

(a) 基础z向平动

图8(a)为无基础激励转子的位移轨迹，从图中可以看出，转子轨迹为呈规则圆形，稳定后位移达到8 μm，这是由于转子不平衡导致的。

图8(b)为x方向基础平动激励下转子的位移轨迹，激励参数取振动幅值为2 mm，振动频率为5 Hz，可以看出在转子不平衡位移的基础上，转子在x方向发生了位移偏移，幅值达到了12 μm，仿真表明x方向基础平动和转子不平衡并不存在耦合。

图8(c)为y方向基础转动激励下转子的位移轨迹，激励参数取偏摆幅度为3°，振动频率为5 Hz，从位移方向上看，y向转动主要影响x方向位移，位移幅值约为15 μm，但不同于图8(b)，转子轨迹不仅在x方向有振动位移，在y方向也存在小范围的位移，相比只有不平衡作用下的8 μm位移，转子在y方向的位移达到11 μm左右，可见径向基础转动对转子径向另一自由度产生了耦合影响，这是基础转动区别于基础平动的又一特质。此外，转子轨迹的对称轴(图中红线)并不关于x轴对称，实际上存在很小的偏移，这是由于基础转动下重力扰动引起的，但偏移影响并不明显，由此表明重力扰动作用对转子影响并不大。

由于实际运动往往是复合运动，同时考虑基础x向平动与y向摆动时，转子轨迹如图8(d)所示，相比图8(c)，在引入x向平动后，复合运动并没有使x向位移增加，反而使位移减小了3 μm，可以看出复合运动使径向耦合作用进一步加剧。

图9主要讨论了轴向基础激励参数对转子轨迹的影响，基础轴向参数往往与实际应用参数相结合，以车辆船舶为例，基础轴向(z向)运动与前进方向相同，并且轴向平动往往处于加速或匀速状态，而轴向转动也比径向转动幅值更大。

图9(a)为z方向基础平动激励下转子的位移轨迹，激励参数为5 m/s2的加速运动，从图中可以看出，转子位移轨迹与图8(a)相同，只存在不平衡的作用，即z向基础平动并不对转子位移产生影响。当然，只存在z向基础平动与不平衡作用的转子是理想情况，当转子偏离质心位置，基础运动引起的附加耦合力矩作用于转子，也会影响转子运动。

图9(b)为z方向基础转动激励下转子的位移轨迹，激励参数取偏摆角度为3°，转动频率为5 Hz，可以看出，基础z向偏摆增大了y向位移，增幅约为7 μm，同时也对x向位移有小幅度影响，仿真表明基础z向转动对转子径向产生了耦合作用，且主要影响转子y向位移。

从附录C，D中表明z向平动常伴随着径向转动项，故引入基础z向平动加速度和y向转动的复合运动，转子轨迹如图9(c)所示，图中转子轨迹是混乱无序的，且有逐步增大的趋势，即系统发散。从能量机理分析，当基础一直处于加速状态，即能量不停输入给转子系统，转子质心发生偏移时，施加在转子上的作用力不断增大，直至系统发生失稳。

改变基础z向平动参数，当基础z向是匀速状态，取速度为5 m/s，同时施加y向的基础转动，转子轨迹如图9(d)所示，对比图9(c)可以看出，系统不再发散，复合运动分别使转子x向和y向位移增加了8 μm、13 μm，仿真表明在z向平动中径向基础转动的耦合作用更加明显。

本节主要研究了基础激励参数对转子轨迹的影响，其主要结论如下：从激励类型上看，径向平动激励使转子在平动方向上发生振动偏移；而径向转动激励不仅影响对应方向的转子振动，还在径向另一自由度上产生耦合作用；径向平动与转动之间也存在耦合作用，甚至可能减弱转子在对应方向上的位移。当只存在轴向平动激励时，虽然会对轴向位移产生影响，但并不影响径向转子位移轨迹；而轴向转动激励还会对径向自由度产生耦合作用；特定的轴向与径向的复合运动可能导致系统发散，在工程应用中应当考虑特定基础激励的影响。

4.2 转子系统位移幅值的变化规律

4.1节重点讨论了转子轨迹的变化规律，本节则主要研究转子振动的位移幅值，为了探究参数之间对转子振动位移幅值的变化规律，参数变化与位移幅值用响应面表达，仿真取基础平动与转动的复合运动，转子转速与不平衡同4.1节，参数变化选取径向平动，径向转动，轴向转动，轴向平动4个变量，转子位移响应如下：

x方向基础平动激励变化下转子位移幅值响应如图10所示，取基础复合运动为x方向平动与y向转动，基础y向转动取5 Hz，0.05 rad的固定参数。从图中可以看出，转子位移幅值随着振动幅值与频率的增大逐渐增大，在低幅值下，近似呈线性关系；在低频率下，位移随幅值变化不大，而在高频率下，位移增长呈现非线性。需要注意的是，在5 Hz与10 Hz处，由于基础y向转动在相等频率以及倍频处与基础x向平动作用相反，转子位移出现塌陷，这是基础复合运动在特定频率下对转子耦合作用的一个特征。

y方向基础转动激励变化下转子位移幅值响应如图11所示，复合运动仍然取x向平动与y向转动，基础x向平动参数取5 Hz，2 mm的固定参数，与图10的变化规律类似，转子位移幅值随着转动幅值与频率的增大也在逐渐增大，同时基础转动与平动的复合作用使得转子位移在频率5 Hz处存在塌陷，但在10 Hz倍频处并不明显，这一现象有待后续进一步探究。

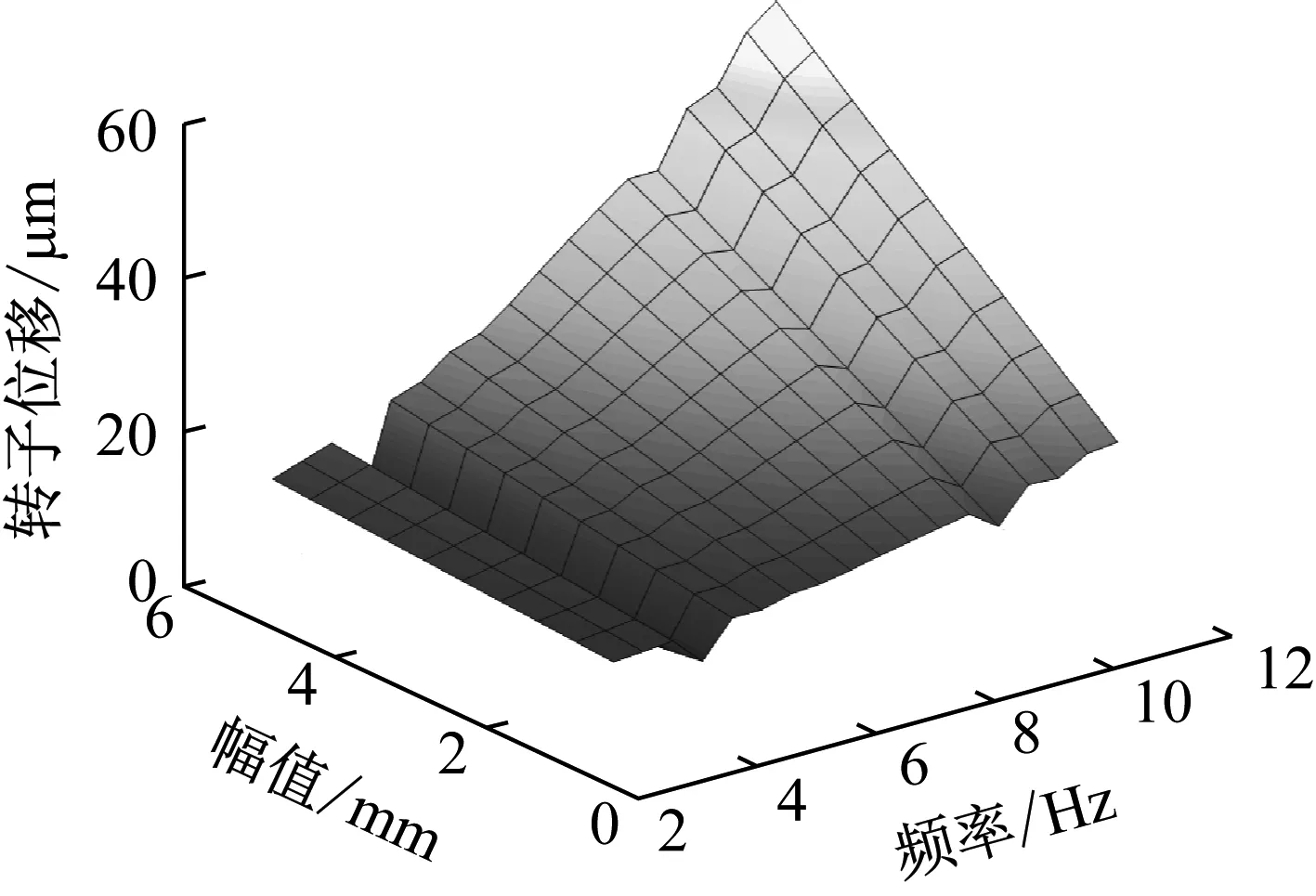
图10 x方向基础平动激励下转子位移幅值Fig.10 Displacement amplitude of rotor under translational excitation of foundation in x direction

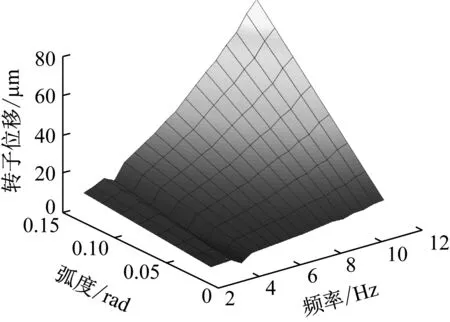
图11 y方向基础转动激励下转子位移幅值Fig.11 Displacement amplitude of rotor under foundation rotation excitation in y direction

z向基础平动激励与径向基础激励有所不同，从4.1节已知，z向平动加速度与y向转动的复合运动会使系统发散。若讨论z向速度参数，并没有幅值和频率两个变量，故选取转子转速作为另一个变量。转子位移幅值响应如图12所示，可以看出前进速度在5～25 m/s变化范围内，基础运动对转子位移幅值的影响近似呈线性关系，转速变化并不影响其线性度，但随着转速的升高，由于刚体模态(约75 Hz)的影响使转子位移先增大后减小。由此仿真结果表明前进速度与转速均独立作用于转子，两者之间并不存在耦合作用。

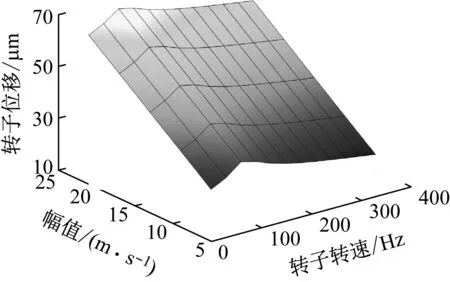
图12 z方向基础平动激励下转子位移幅值Fig.12 Rotor displacement amplitude under z-direction foundation translational excitation

z方向基础转动激励变化下转子位移幅值响应如图13所示，复合运动取x向平动与z向转动，x向平动参数同图11。从仿真结果可以看出，与径向基础转动不同，z向基础转动虽然在转动幅值和频率上取值均大于y向基础转动，但其转子位移幅值远小于径向基础转动产生的几十微米，最高只达到了8 μm。z向转动频率变化对转子位移幅值影响并不大，但基础平动与转动的复合作用在频率5 Hz和10 Hz处依然明显，且在倍频处影响更大；而转动幅值的影响近似呈线性关系，并不受频率变化影响。

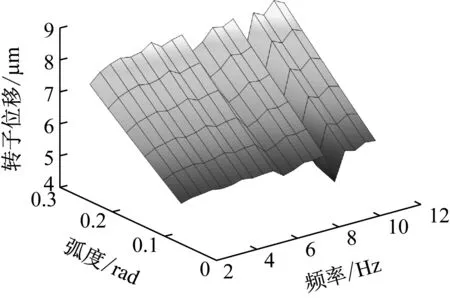
图13 z方向基础转动激励下转子位移幅值Fig.13 Rotor displacement amplitude under z-direction foundation rotation excitation

本节讨论了基础激励参数对幅值的影响规律，基本结论如下：基础径向平动、转动在影响规律上是一致的；基础激励频率对转子位移影响要比振动幅值更大，呈非线性关系，但同时要注意基础复合运动在同频及倍频的转子位移衰减；对于基础轴向运动，振动幅值变化则需要重点关注，虽然转子在刚性转速范围内，但需要注意在转值升速过程中刚体模态的影响。