任意边界条件下弹性梁耦合振动特性分析
2022-09-23李海虹郭山国刘志奇李王铎
李海虹,王 昊,郭山国,刘志奇,李王铎
(1.太原科技大学 机械工程学院,太原 030024;2.河北机电职业技术学院 机械工程系,河北 邢台 054000)
电主轴是数控机床和某些工业机器人的核心功能部件,建立主轴单元横向、纵向以及扭转耦合振动模型对加工精度的量化分析具有重要意义。振动特性研究中,主轴单元多简化为弹性梁模型,并通过有限元方法求解。有限元方法是一种纯数值方法,当模型边界条件和几何参数发生改变,需要对模型进行重构[1],所以在振动机理及参数特性分析等方面,理论建模对结构动态设计及优化是必要的。
理论建模中,不同的位移函数的构造推导出不同的分析模型。Zemskov等[2]基于传统傅里叶级数形式的解研究了Euler-Bernoulli梁的非定常振动。Motaghian等[3]基于正弦和余弦傅里叶级数形式的解研究了变截面梁的自由振动。Yayli[4]基于传统傅里叶级数形式的解研究了具有旋转约束边界条件的纳米梁的自由振动。Li[5]提出了一种改进傅里叶级数方法(improved Fourier series method)分析任意边界支撑下梁结构的弯曲振动特性,通过引入辅助函数解决传统傅里叶级数在整个求解区域内周期展开时在边界上存在的不连续现象。Lü等[6]引入能量原理,将改进傅里叶级数方法应用于任意弹性边界条件下梁结构的横向振动分析。杜敬涛等[7-9]采用改进傅里叶级数法研究了任意边界条件下弹性杆的扭转振动以及非局部弹性杆和变截面弹性杆的纵向振动。Chen等[10]采用改进傅里叶级数法研究了具有弹性边界支撑的旋转梁的横向振动。赵雨皓等[1]采用改进傅里叶级数法对轴向载荷条件下弹性边界约束梁结构的横向振动进行了研究。Zhang等[11]采用改进的傅里叶级数法研究了三维耦合梁的自由振动特性。Nie等[12]采用改进傅里叶级数法研究了不同边界条件下弯曲梁的平面内和平面外自由和受迫振动。Mahapatra等[13-14]采用改进傅里叶级数法研究了弹性边界下有阻尼和无阻尼Euler-Bernoulli梁的受迫振动响应以及矩形板的面内振动特性。
Shi等[15]基于改进傅里叶级数法进一步提出了谱几何方法(spectro-geometric method)。该方法构造的位移函数的辅助函数采用三角级数形式,在满足收敛性要求的同时使得方程积分和微分运算更加简便。Shi等[16]采用谱几何法研究了T形板的面内自由和受迫振动。Wang等[17-18]采用谱几何法研究了弹性板浸入水中以及与声腔耦合振动的声辐射特性。鲍四元等[19-20]采用谱几何法研究了弹性边界下非局部梁的横向振动和纳米杆的纵向振动。但是现有文献尚且没有对梁结构扭转振动,及其横向、纵向和扭转耦合振动采用谱几何法进行分析。
本文将谱几何法扩展到弹性梁的扭转振动建模,统一弹性梁横向、纵向和扭转振动位移函数表示形式,建立了任意边界条件下弹性梁横向、纵向和扭转振动模态特性的统一参数化求解模型,完成模型验证,并研究边界约束弹簧刚度对弹性梁横向、纵向和扭转振动特性的影响。
1 理论模型
1.1 模型描述
本文使用弹性梁模型模拟主轴单元模型,采用边界约束弹簧组模拟任意边界条件,相应的全局坐标系如图1所示。在直角坐标系的梁模型两端使用6组连续的边界约束弹簧,包括3组线性约束弹簧,分别沿x-、y-、z-方向,3组旋转约束弹簧,分别绕x-、y-、z-方向。通过将相应的边界约束弹簧刚度值设定为0到无穷大数可以模拟任意边界条件。弹簧形式见表1。
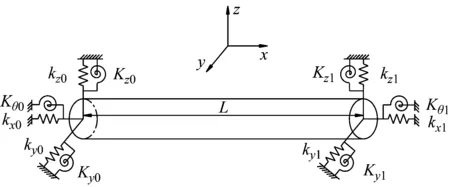
图1 任意边界条件下弹性梁耦合振动分析模型Fig.1 Coupling vibration analysis model of the elastic beam with arbitrary boundary conditions

表1 弹簧组刚度变量定义表Tab.1 Definition table of spring group stiffness variable
1.2 位移函数的级数表示
假设弹性梁模型为Euler-Bernoulli梁。以往研究中采用改进傅里叶级数法构造的位移函数多使用多项式或者多项式与三角级数相乘的形式作为傅里叶级数的辅助函数。此方法所构造的位移函数会使得结构振动特性的求解运算过程相对复杂,不利于提高计算效率。本文采用谱几何法描述弹性梁耦合振动的位移函数。位移函数的主函数和辅助函数都表示为三角级数形式,三角级数在微分和积分操作中的“偶不变性”使得整个计算更加简便。
本文将弹性梁耦合振动离散为沿x-纵向振动、沿y-、z-横向振动和绕x-轴线扭转振动。将弹性梁沿x-、y-、z-方向的位移函数和绕x-轴线的转角函数分别表示为
(1)
(2)
(3)
(4)
(5)
式中:An,Bn,Cn和Dn分别代表位移函数的未知傅里叶级数展开系数;ω为圆频率;eiωt为简谐时间因子;在后续推导中为了简化将忽略该时间因子。
由Euler-Bernoulli梁理论可知,梁模型沿x-纵向振动控制微分方程和绕x-轴线扭转振动控制微分方程都是二阶偏微分方程。当位移函数采用传统傅里叶级数形式表示时,在梁两端会出现位移函数一阶导数不连续和二阶导数跳跃现象,对任意边界条件并不适用。因此,每个位移函数在沿x-纵向和绕x-轴线扭转方向的分量除了无穷项余弦级数外还需要增加两项正弦级数(对应于式(1)和(4)中的n=-2)作为辅助函数。Li[21]从数学上验证可知,位移函数的级数表达式对于∀(x)∈R:(0,L)能够展开并且一致收敛于任意函数f(x)∈C1。因此可以实现在任意边界条件下位移函数一阶导数连续和二阶导数各点存在。
同理,梁模型沿y-横向振动控制微分方程和沿z-横向振动控制微分方程都是四阶偏微分方程。通过在每个方向上增加四项正弦函数(对应于式(2)和(3)中的n=-4)作为辅助函数,从数学上可知,位移函数的级数表达式对于∀(x)∈R:(0,L)能够展开并且一致收敛于任意函数f(x)∈C3。因此可以实现在任意边界条件下位移函数三阶导数连续和四阶导数各点存在。
本节采用基于改进傅里叶级数法的谱几何法建立了弹性梁纵向、横向和扭转振动的位移函数,在满足边界连续性的同时实现了弹性梁纵向、横向和扭转振动位移函数表示形式的统一。
1.3 模型求解
在采用谱几何法建立弹性梁模型纵向、横向和扭转振动的位移函数之后,需要求解相应位移函数的未知级数展开系数。本文基于Hamilton原理从能量角度建立包含弹性梁纵向、横向和扭转振动的系统拉格朗日函数,采用Ritz方法对未知系数取驻值,再通过求解即可分别获得弹性梁结构纵向、横向和扭转振动的模态特性参数。在求解过程中,4个位移函数的傅里叶级数表达式需要按照n=N进行截断。
Hamilton原理的表达式为

(6)
式中:V为弹性梁的总势能;T为弹性梁的总动能。
对于图1所示的弹性梁模型,总势能的表达式为
V=Vp+Vs
(7)
式中:Vp为弹性梁自身的应变势能;Vs为两端约束弹簧的弹性势能;表达式分别为
(8)
(9)
式中:E为弹性模量;S为横截面面积;Iy、Iz分别为对y轴、对z轴的惯性矩;G为切变模量;J为极惯性矩。
弹性梁模型的总动能表达式为
(10)
式中:ρ为材料密度;S为横截面面积;J为极惯性矩。
弹性梁模型的拉格朗日函数可以表示为
L=Vp+Vs-T
(11)
将位移函数式(1)~(4)代入到函数式(11)中,采用Ritz方法使式(11)对其中的傅里叶级数展开系数An,Bn,Cn和Dn求极值
(12)
求解式(12)得到4个方程的线性方程组,将方程组写为矩阵表达形式
(K-ω2M)X=0
(13)
式中:K为系统的刚度矩阵;M为系统的质量矩阵;X为包括所有未知傅里叶级数展开系数的向量,可表示为
(14)
通过求解式(13)所示的标准特征值问题就可以得到弹性梁模型纵向、横向和扭转振动的模态特性(固有频率及其对应的特征向量)。将每阶固有频率所对应的特征向量系数代入至位移函数式(1)~(4)即可得到相应的物理模态振型。由建立的理论模型可知,本文统一了弹性梁纵向、横向和扭转振动特性计算模型,即统一了弹性梁纵向、横向和扭转振动模态特性求解方程。
2 模型验证与分析
在本章中,对不同边界条件下弹性梁结构横向、纵向和扭转振动特性进行计算分析,通过将本文计算结果与文献解结果进行对比,验证所建立的理论模型和运算程序的正确性。随后分析边界约束弹簧刚度值对弹性梁耦合振动固有频率的影响。表2给出了弹性梁模型的材料和几何参数。
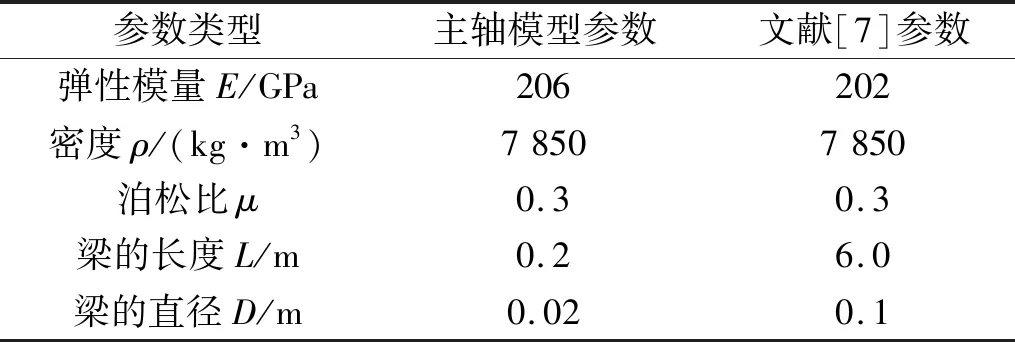
表2 梁模型的材料和几何参数值Tab.2 Material and geometric parameters of beams
2.1 收敛性研究
在计算过程中,需要首先验证构造的位移函数及确定的级数截断数的收敛性和计算精度。本小节首先对弹性梁结构采用本文方法得到的扭转和纵向振动的固有频率收敛性进行分析,然后对其横向、纵向和扭转耦合振动对应的模态振型特性进行分析。
将本文弹性梁扭转振动固有频率求解结果与文献[7]计算结果和有限元求解结果进行对比,计算中梁模型参数都按文献选取如表2所示。选择固支-固支边界条件,选取边界约束弹簧刚度值如表3所示,通过将边界约束弹簧刚度值设定为0模拟自由边界,设定为无穷大数模拟固支边界。通过预计算,当相应边界旋转约束弹簧刚度值设定为1010时,弹性梁固支-固支边界下扭转振动固有频率趋于定值,满足相应固支边界模拟。同理,当相应边界约束弹簧刚度值设定为1015时,满足弹性梁纵向振动和横向振动固支边界模拟。表4为弹性梁的位移函数取不同级数截断数时得到的前6阶扭转振动的固有频率。

表3 不同边界条件和振动类型对应约束弹簧的刚度值Tab.3 Stiffness values of restraint springs under different boundary conditions and model types
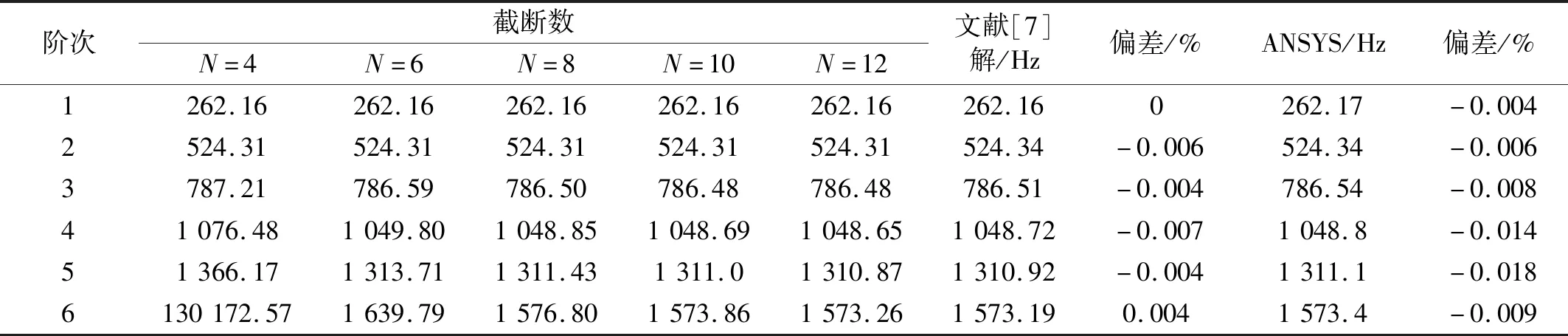
表4 固支-固支弹性梁在不同截断数下前6阶扭转振动固有频率Tab.4 The first 6 torsional vibration natural frequencies of the clamped-clamped elastic beam with different truncation numbers
由表4可以看出当截断数取N=12时,弹性梁扭转振动的固有频率计算结果与文献[7]解最大偏差为-0.007%,与ANSYS解最大偏差为-0.018%,验证了本文方法的正确性。同时,随着截断数的增大,计算精度逐渐提高,文献中取N=35,而本文较小的截断数即可得到较高的计算精度,表明本文方法具有较快的收敛性。后面的计算中,本文截断数均取N=12。
将本文弹性梁纵向振动固有频率求解结果与文献[22]中经典解结果进行对比。选择固支-固支边界条件,计算中弹性梁参数按主轴简化模型参数选取如表2所示,边界约束弹簧刚度值选取如表3所示,得到弹性梁前6阶纵向振动的固有频率如表5所示。
由表5可以看出本文弹性梁纵向振动的固有频率计算结果与文献[22]经典解最大偏差为0.02%,验证了本文方法求解弹性梁纵向振动固有频率的正确性。应用谱几何法求解梁模型横向振动固有频率的收敛性已在文献[19]中研究,本文将不再单独分析。
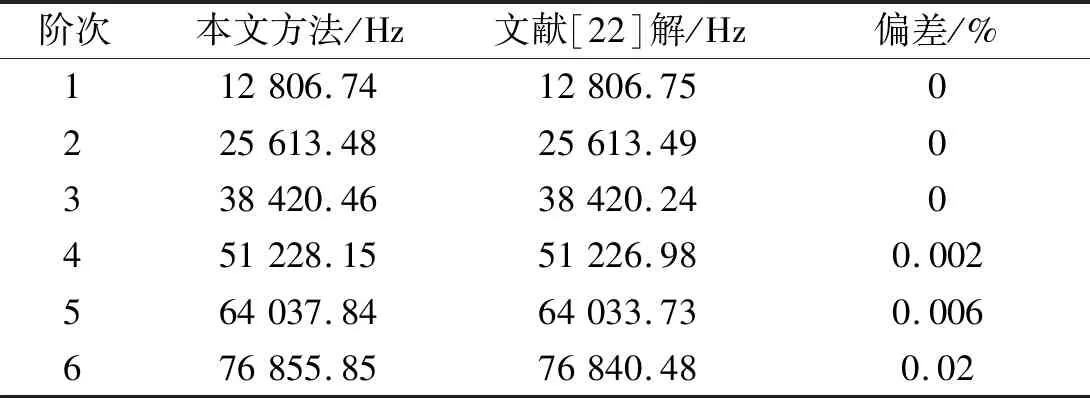
表5 固支-固支弹性梁前6阶纵向振动固有频率Tab.5 The first 6 longitudinal vibration natural frequencies of the clamped-clamped elastic beam
由上述分析可知,当梁模型的材料和几何形状改变时,无需重新进行理论推导和建模,仅需要改变相应参数值,可以实现弹性梁结构参数化研究,方便结构优化设计。
通过将特征方程(13)求解所得到的弹性梁纵向、横向和扭转振动的每阶固有频率对应的无量纲化特征向量系数代入位移函数式(1)~(4)便可得到相应阶次的无量纲化模态振型图。弹性梁参数按主轴简化模型参数选取如表2所示,边界约束弹簧刚度值选取如表3所示,得到固支-自由边界条件下弹性梁纵向、横向和扭转振动的前4阶无量纲模态振型如图2所示。

(a) 第一阶
由图2可以看出弹性梁纵向、横向和扭转振动模态振型左端位移为0,右端存在位移,符合固支-自由边界条件。从弹性梁前4阶模态振型图可以看出,弹性梁每一阶振动中存在纵向模态、横向模态和扭转模态,说明弹性梁的振动是由3种振动耦合而成。此外,根据弹性梁结构特性,在低阶模态中,横向模态(弯曲模态)为主导模态。
2.2 边界约束弹簧刚度对弹性梁耦合振动特性影响
本节对弹性梁在不同边界约束弹簧刚度下的横向、纵向和扭转振动的第一阶模态特性进行研究,以实现本文方法对任意边界条件下的弹性梁耦合振动特性进行分析。计算中弹性梁参数按主轴简化模型参数选取如表2所示。
(1)边界约束弹簧刚度对弹性梁扭转振动影响
为模拟弹性梁扭转振动从两端自由到两端固支的边界条件,将两端约束弹簧旋转刚度Kθθ,Kθ1从0.000 1 N·m/rad增加到1010N·m/rad,其它边界约束弹簧刚度设置为0。图3是弹性梁扭转振动第一阶固有频率随边界约束弹簧旋转刚度变化的三维图,其中坐标轴取边界约束弹簧刚度值的对数,以下小节坐标轴设置同理。

图3 边界约束弹簧旋转刚度对弹性梁扭转振动的影响Fig.3 Influence of boundary restraining rotational stiffness on the torsional vibration of elastic beam
由图3可知,随着边界约束弹簧旋转刚度的增大,弹性梁第一阶扭转振动固有频率逐渐增大。当约束弹簧旋转刚度在0~105N·m/rad范围内变化时,弹性梁固有频率变化明显,当约束弹簧旋转刚度增大至105N·m/rad以上时,弹性梁固有频率变化微弱且趋于一个定值。因此可知弹性梁第一阶扭转振动固有频率随旋转刚度值变化存在敏感区间,该区间为0~105N·m/rad。
(2)边界约束弹簧刚度对弹性梁纵向振动影响
为模拟弹性梁纵向振动从两端自由到两端固支的边界条件,将两端约束弹簧平动刚度kx0,kx1从0.000 1 N/m增加到1015N/m,其它边界约束弹簧刚度设置为0。图4是弹性梁纵向振动第一阶固有频率随边界约束弹簧平动刚度变化的三维图。
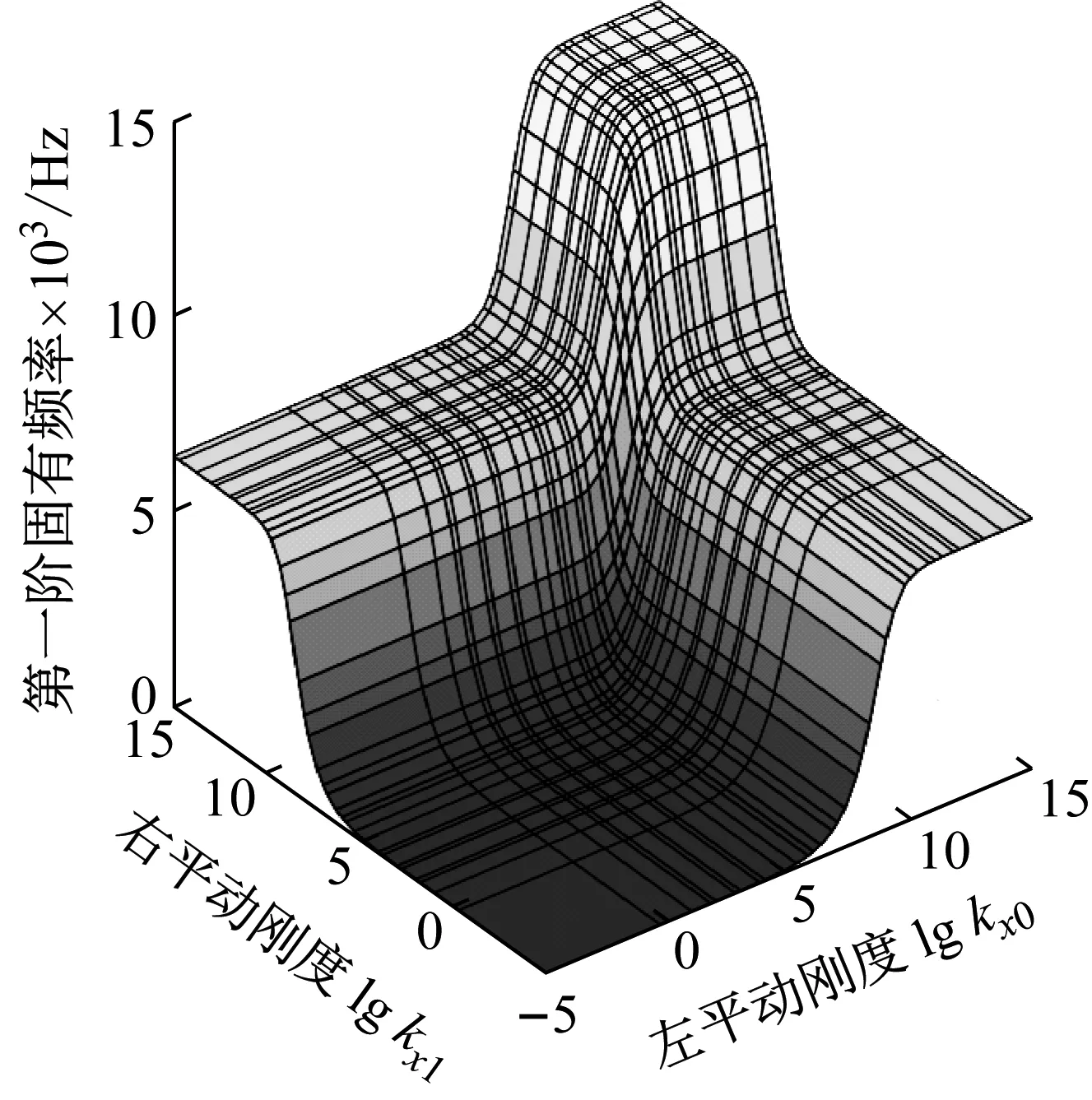
图4 边界约束弹簧平动刚度对弹性梁纵向振动的影响Fig.4 Influence of boundary restraining translational stiffness on the longitudinal vibration of elastic beam
由图4可知,弹性梁第一阶纵向振动固有频率随约束弹簧平动刚度的增大而增大。当约束弹簧平动刚度在105~1011N/m范围内变化时,弹性梁固有频率变化明显,当约束弹簧平动刚度增大至1011N/m以上时,弹性梁固有频率变化微弱且趋于一个定值。因此可知弹性梁第一阶纵向振动固有频率随平动刚度值变化存在敏感区间,该区间为105~1011N/m。
(3)边界约束弹簧刚度对弹性梁横向振动影响
本小节首先研究边界约束弹簧平动刚度对弹性梁y-向横向振动的影响,对弹性梁z-向横向振动的影响同理。将约束弹簧旋转刚度设置为Ky0=0 N·m/rad,Ky1=0 N·m/rad,将约束弹簧平动刚度ky0,ky1从0.000 1 N/m增加到1015N/m,其它边界约束弹簧刚度设置为0,模拟弹性梁y-向横向振动从两端自由到两端简支的边界条件。图5是弹性梁y-向横向振动第一阶固有频率随边界约束弹簧平动刚度变化的三维图。

图5 边界约束弹簧平动刚度对弹性梁横向振动的影响Fig.5 Influence of boundary restraining translational stiffness on the transverse vibration of elastic beam
由图5可知,弹性梁第一阶y-向横向振动固有频率随约束弹簧平动刚度的增大而增大。当约束弹簧平动刚度在102~109N/m范围内变化时,弹性梁固有频率变化明显,当约束弹簧平动刚度增大至109N/m以上时,弹性梁固有频率变化微弱且趋于一个定值。因此可知弹性梁第一阶y-向横向振动固有频率随平动刚度变化存在敏感区间,该区间为102~109N/m。
其次研究边界约束弹簧旋转刚度对弹性梁y-向横向振动的影响。通过将约束弹簧平动刚度设置为ky0=1015N/m,ky1=1015N/m,将约束弹簧旋转刚度Ky0,Ky1从0.000 1 N·m/rad增加到1015N·m/rad,其它边界约束弹簧刚度设置为0,模拟弹性梁y-向横向振动从两端简支到两端固支的边界条件。图6是弹性梁y-向横向振动第一阶固有频率随边界约束弹簧旋转刚度变化的三维图。
由图6可知,弹性梁第一阶y-向横向振动固有频率随约束弹簧旋转刚度的增大而增大。当约束弹簧旋转刚度在102~107N·m/rad范围内变化时,弹性梁第一阶固有频率变化明显,约束弹簧旋转刚度增大至107N·m/rad以上时,弹性梁固有频率变化微弱且趋于一个定值。因此可知弹性梁第一阶y-向横向振动固有频率随旋转刚度变化存在敏感区间,该区间为102~107N·m/rad。
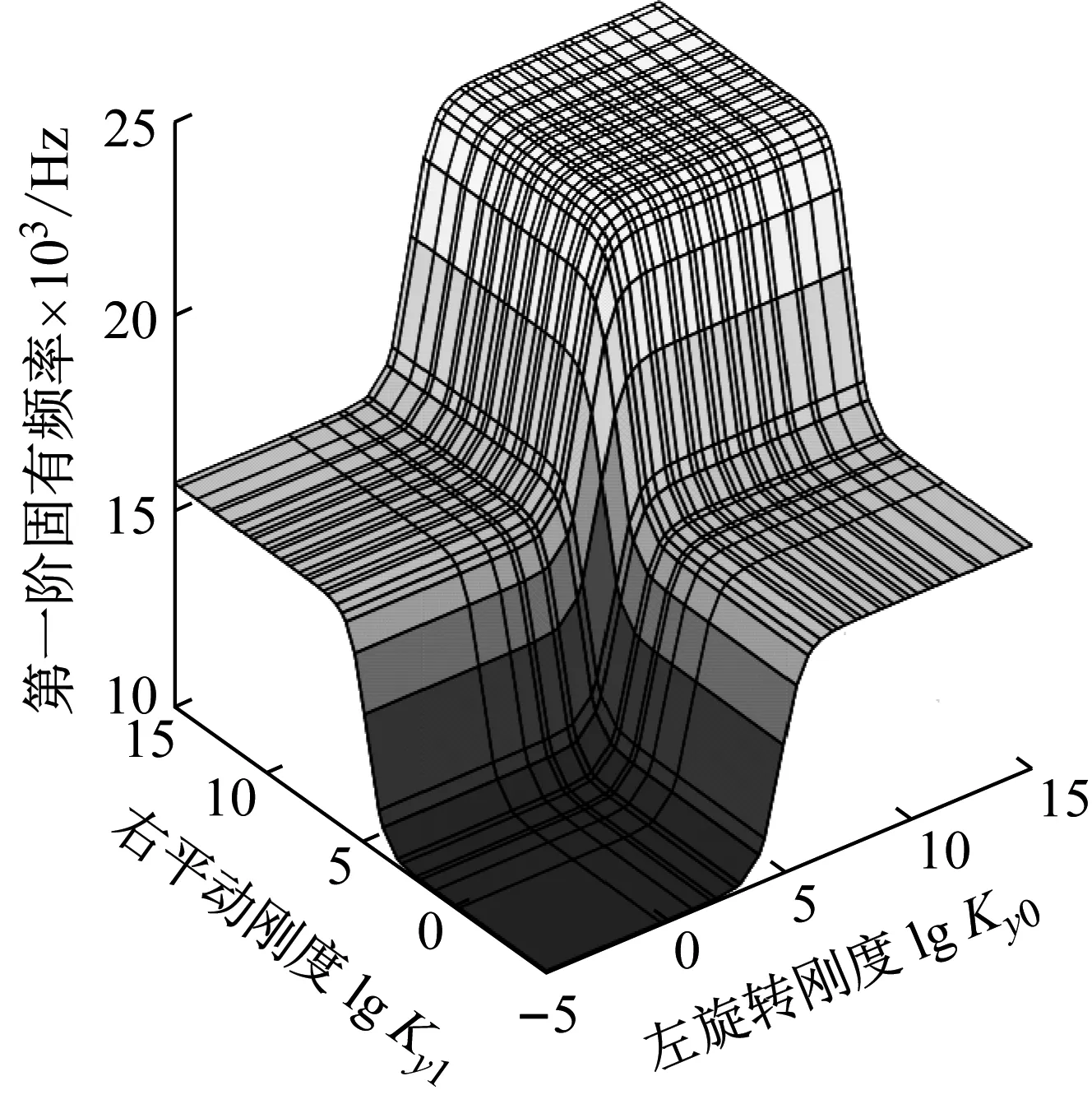
图6 边界约束弹簧旋转刚度对弹性梁横向振动的影响Fig.6 Influence of boundary restraining rotational stiffness on the transverse vibration of elastic beam
综上所述,通过更改弹性梁两端相应边界约束弹簧的平动刚度、旋转刚度值即可实现模型在任意边界约束条件下的横向、纵向和扭转振动特性分析。同时由上文分析可知,弹性梁耦合振动固有频率随边界约束弹簧刚度变化都存在刚度影响敏感区域,当刚度值在此范围内变化时可以调整弹性梁耦合振动特性。
3 结 论
本文将基于改进傅里叶级数法的谱几何法应用到弹性梁的扭转振动分析并建立了任意边界条件下弹性梁的横向、纵向和扭转耦合振动特性统一计算模型。结论如下:
(1)弹性梁模型的横向、纵向和扭转振动位移函数都表示为一种谱几何形式的改进傅里叶级数,统一了弹性梁横向、纵向和扭转振动位移函数的表示形式和模态特性的求解方程。
(2)在数值计算中,较小的位移函数级数截断数即可得到较高的计算精度,表现出较快的收敛性。
(3)在弹性梁结构两端引入边界约束弹簧组,当边界条件改变时,通过改变其刚度值大小从0到无穷大模拟。通过改变弹性梁几何参数和材料参数可以实现相应参数化研究,不需要重新进行理论建模和更改程序,方便对结构进行优化设计。
(4)计算出弹性梁横向、纵向和扭转振动特性随两端边界约束弹簧刚度变化的敏感区间。结构耦合振动特性可以通过在此区间内改变弹簧刚度值进行调整。为实际工程中改变结构边界约束刚度以避免在外部激励下发生共振提供参考。
