基于相位补偿的非理想无线轨道角动量复用通信系统研究

王 洋 修艳磊 胡 韬 施盼盼 廖 希

(重庆邮电大学通信与信息工程学院 重庆 400065)

(移动通信教育部工程研究中心 重庆 400065)

(移动通信技术重庆市重点实验室 重庆 400065)

1 引言

随着现代移动通信技术的发展，传统以时间、频率和空间为主体的复用技术几乎被开发到了极限，而智能终端设备的爆发式增加，使得无线通信系统对信道容量的需求急剧增长[1,2]。为了满足日益增加的通信容量需求，亟需一种新的复用通信技术。轨道角动量(Orbital Angular Momentum, OAM)作为第6代移动网络(the 6th Generation mobile networks, 6G)中的潜在技术之一，其不同整数模态间存在的正交性，使得无线通信系统可以在不依赖时间、空间和频率等资源的情况下，极大地提升系统信道容量，为解决当前无线通信系统面临的资源短缺问题提供了一个全新的选择[3-6]。因此，OAM在无线通信领域受到了许多学者和机构的研究。

然而，实际无线通信环境通常是复杂多变的，传输路径损耗、极端天气影响、多径效应和收发端天线阵列未对齐等都会对无线OAM通信系统性能造成严重影响。为了研究多径效应的影响，Jie等人[12]建模了一种典型峡谷6径OAM-MIMO通信模型，分析了多径效应对OAM相位、模态谱和接收信号功率造成的影响。Yan等人[13]在毫米波频段进行了两径信道OAM复用通信实验，其结果表明，多径效应会造成严重的OAM模态间干扰，降低系统性能。为了解决多径效应造成的影响，Liang等人[14]联合正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)技术，并在接收端采用全相位补偿法来减轻多径效应带来的干扰。此外，收发端天线非对齐也会影响OAM通信系统性能，2014年，Shin等人[15]建模了LoS条件下收发天线阵列非对齐时的OAM通信系统，其研究结果表明，非对齐同样会使OAM模态间产生严重干扰，从而降低系统性能。为了减轻非对齐带来的影响，Chen等人[16]在2018年提出了一种波束控制方案，该方案通过调整收发波束的相位，以此减轻了非对齐造成的相位偏差，提升了非对齐OAM通信系统性能。Jing等人[17]在2019年提出了一个信道独立的波束赋形方案，通过将非循环矩阵转换为循环矩阵来将收发天线阵列等效为理想对齐，以此提升系统性能。综上所述，尽管当前对多径或者收发天线未对齐场景的OAM-MIMO通信进行了一定的研究，然而在实际通信环境中，多径效应和非对齐通常同时存在。因此，如何改善非理想条件OAM-MIMO复用通信系统性能值得进一步研究。

本文考虑非对齐和多径效应同时存在的场景，如会议室、走廊、地下通道、巷道和楼梯间等室内点对点通信，建立了一种常规峡谷毫米波OAM-MIMO 10射线传播模型，针对非对齐和多径效应造成的模态间干扰问题，提出了一种平均相位补偿和迭代功率分配(Average Phase Compensation and Iterative Power Allocation, APC-IPA)联合优化方案。其中，APC方案是利用泰勒展开法求得各条路径的相位偏差与其均值，并通过在接收端对各信道相位偏差进行补偿来减轻系统中的干扰，与文献[14]中的全相位补偿方案相比，系统计算复杂度得到了较大的降低；IPA方案则是基于每个子信道的信干噪比(Signal to Interference Noise Ratio, SINR)不断迭代优化其所分配的功率以进一步提升系统信道容量，并且与传统方法相比，APC-IPA方案的算法迭代次数更低。

2 系统模型

本文建立的峡谷OAM-MIMO 10射线传播模型如图1所示。其中，发射机(Transmitter, Tx)位于峡谷一侧的钢架上，接收机(Receiver, Rx)则为用户的移动设备。Tx和Rx均采用均匀圆形天线阵列(Uniform Circular Array, UCA)，并且它们的阵元数都为N。假设Tx和Rx都垂直于地面放置，且只在高度上存在一定差距，即Tx和Rx在Z轴方向上会存在着轴偏差。此外，本文采用镜面法来对不同路径电磁波的传播进行建模[18]。由于高阶OAM反射信号有着超高的路径损失，因此，本文只考虑1阶和2阶OAM反射信号。基于此，该模型下的MIMO信道矩阵可以建模为[19]

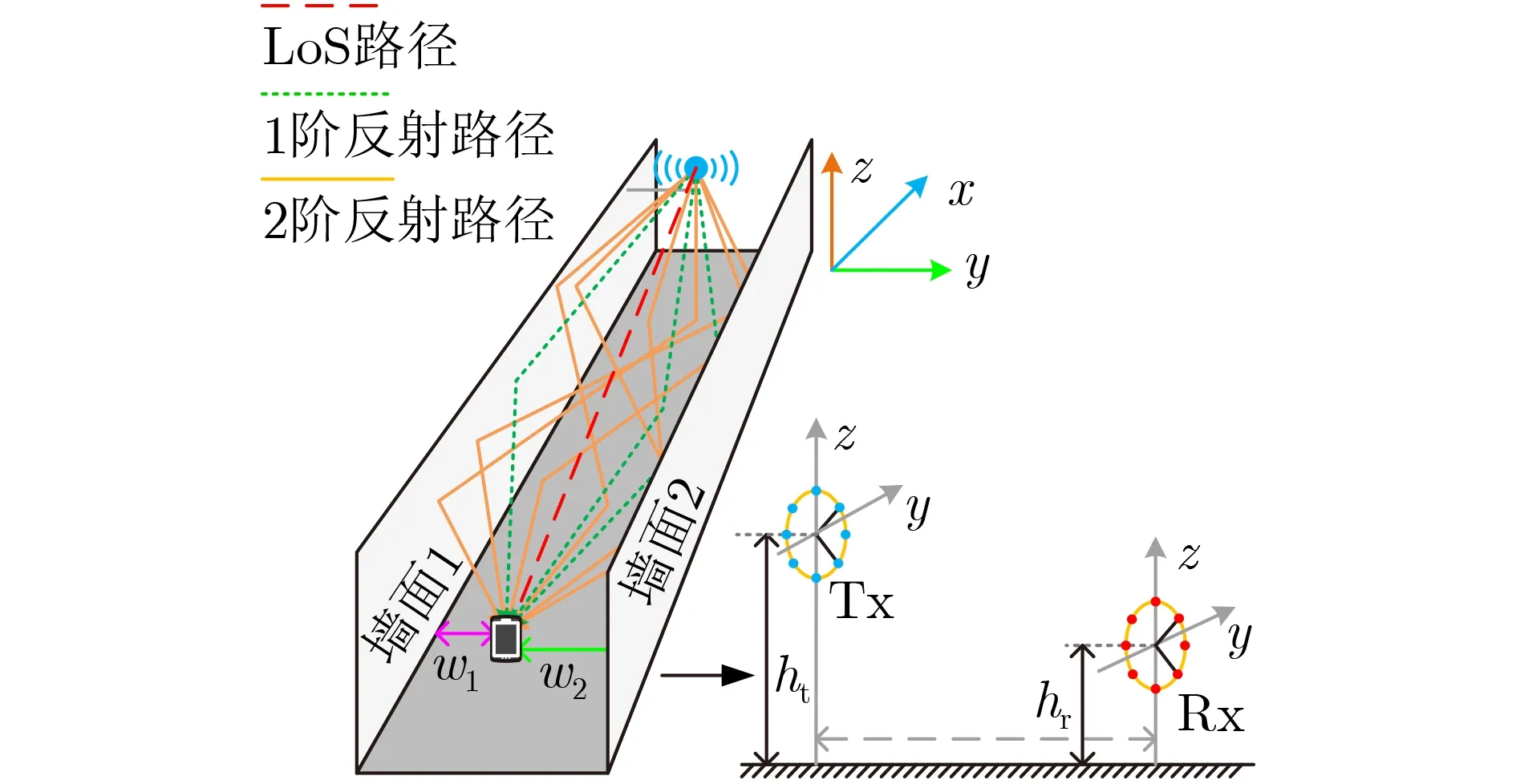
图1 基于未对齐收发天线阵列的街道峡谷OAM-MIMO 10射线传播模型

其中，dR(m, n)是第n个发射天线单元与第m个接收天线单元在反射路径下的传输距离，ΔtR(m, n)= [dR(m ,n)-dLoS(m, n)]/c为反射路径与LoS路径之间的传输时延，c为光速。γR是反射系数。

因此，对于图1的各条1阶反射路径，其发射天线单元n到接收天线单元m的传输距离分别表示为

其中，dR2,1(m, n)表示信号先后经过地面和墙面1反射后到达接收天线单元的传输距离，dR2,2(m, n)表示信号先后经过地面和墙面2反射后到达接收天线单元的传输距离，dR2,3(m, n)表示信号先后经过墙面1和墙面2反射后到达接收天线单元的传输距离。

基于上述所求得的传输距离，对于图1的10射线模型，其LoS路径的时域信道响应可表示为式(2)，其1阶反射路径和2阶反射路径的时域信道响应则可分别将dR1,v(m, n)和dR2,k(m, n)代入式(4)求得。然后，可分别得到LoS路径、1阶反射路径和2阶反射路径在频域下的信道响应为

3 相位补偿与功率分配联合优化方案

在OAM-MIMO复用通信系统中，当只考虑LoS传播路径且收发天线阵列正对齐时，信道矩阵HLoS是一个循环矩阵，它可以被OAM模态复用矩阵WLoS和OAM模态解复用矩阵Wr对角化[16]。此时，收发端通过对涡旋信号的复用和解复用能够实现各个OAM模态的相互正交，使得系统拥有良好的通信性能。然而，当收发天线阵列未对齐或者存在多径传播时，如图1所示OAM-MIMO 10射线的传播模型，系统信道矩阵H的相位会产生一定偏差。这将导致信道矩阵H不再是一个循环矩阵，无法被OAM模态复用和解复用矩阵对角化，从而使得不同OAM模态间的正交性被破坏。因此，对于多模态OAM-MIMO复用系统，此时传输的OAM模态间会发生严重的串扰，系统性能也会急剧下降。

为了更加清晰地说明这一现象，图2对比了LoS路径和非视距(Non-Line of Sight, NLoS)路径的信道容量，以及收发阵列未对齐对LoS路径信道容量的影响。从中可以看到，在LoS路径，当收发天线由对齐变成未对齐时，系统在SNR = 20 dB处的容量由约1.9133 bit/(s·Hz)下降到了约0.0493 bit/(s·Hz)；而在NLoS路径，其在SNR = 20 dB处的系统容量更是降低到了约1.35×10-4bit/(s·Hz)。

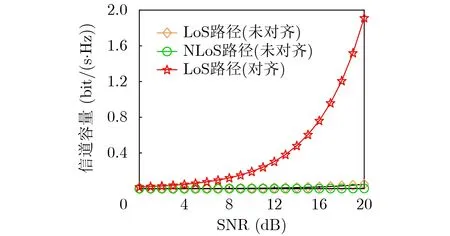
图2 不同路径下的信道容量比较

3.1 APC方案

为了解决上述收发阵列非对齐和多径效应带来的性能问题，本文提出了一种APC方案，其原理是对来自非对齐和多径效应的相位偏差进行补偿，以此尽可能大地减少它们所造成的模态间干扰，提升系统性能。

当接收端已知信道状态信息(Channel State Information, CSI)时，各条路径来自非对齐和多径的相位偏差可以很容易地利用式(22)到式(28)的方法提取出来，从而在接收端利用相位补偿消除上述的相位偏差。当只考虑LoS路径时，利用该相位补偿法得到OAM信道矩阵HOAM一共会有3N次复数乘法(其中，收发阵元数都为N)[21]，然而，在多径场景中，当对每条路径的偏差进行相位补偿时，由于每条路径CSI的不同，一共需要做S × 3N次复数乘法，其中，S是路径数。另外，接收端实际收到的是来自各条路径的和信号，要把每条路径的信道信息HLoS,HR1,v和HR2,k等从H中分离出来并得到相位偏差，这对系统硬件的计算能力有着较大需求。为了降低实际中的计算复杂度，降低成本，本文采用了APC法，即将所有路径的平均相位偏差作为相位补偿因子，相比于前文中对每条路径进行单独相位补偿，平均相位补偿法求取HOAM时相当于只有1条路径，一共只需要做3N次复数乘法，降低了S倍，并且对于路径越多的场景，计算复杂度的降低越大。此外，在求取平均相位偏差时，也不再需要单独求取每条路径信道状态信息，总相位偏差可直接从H中得到，这无疑也大大降低了系统计算复杂度。因此，基于APC方案，所有路径的相位偏差均值表示为

3.2 基于SINR的IPA算法

3.1节提出的平均相位补偿法能够减轻系统中多径效应和非对齐造成的相位偏差，降低模态间干扰，但由于OAM模态的发散性，不同OAM模态信道间的通信质量仍存在着较大的差距。因此，为了进一步提升系统的性能，还需要对系统的功率分配方案进行优化。

由于本文中多径效应和非对齐造成的干扰会影响系统信道容量，而常规的注水功率分配算法是基于信号的信噪比(Signal Noise Ratio, SNR)来进行功率分配的[14]，并未考虑来自干扰项的影响。因此，本文充分考虑OAM模态间干扰，提出了一种基于SINR的IPA算法，其主要步骤为：

Pt为总发射功率。

(3) 计算前后两次不同功率分配方案得到的信道容量差值，即ΔC(i)= C(i)-C(i-1)，判断差值ΔC(i)与极小值ε的大小。若ΔC(i)≤ ε，则将第i-1次的功率分配方案作为最终输出的功率分配方案，若ΔC(i)＞ ε，则回到步骤2继续更新功率分配方案，直至满足输出条件。

最后，算法的详细步骤如表1所示。

表1 IPA算法

4 实验与仿真

实验仿真参数设置如下：传输信号频率设置为毫米波频段，频率f = 30 GHz，发射天线阵列半径Rt和接收天线阵列半径Rr都为5λ，发射机高度ht为200λ，接收机高度hr为150λ，接收机到左右墙面的宽度w1和w2分别为180λ和120λ，发射天线阵列和接收天线阵列的阵元数N为8，传输的OAM模态集合为L = {-3, -2, -1, 0, 1, 2, 3}，传输距离D为20λ。

图3给出了不同优化方案下信道容量随信噪比的变化情况。其中，图3(a)对比了不采用APC方案时，分别采用EPA算法和IPA算法进行功率分配所得到的信道容量。图3(b)则对比了常规MIMO、采用APC-EPA方案、APC-IPA方案和IPA-全相位补偿方案的信道容量。从图3(a)可以看到，随着信噪比的增加，采用IPA功率分配得到的信道容量要明显高于采用EPA方案的，但是由于相位偏差的存在，它们在SNR = 20 dB处的信道容量都低于0.1 bit/(s·Hz)。然而当APC方案被采用后，系统信道容量得到了明显提升，在SNR = 20 dB时，采用APC-IPA方案的信道容量约为2.461 bit/(s·Hz)，采用APC-EPA方案的信道容量约为0.852 bit/(s·Hz)，它们分别是EPA方案(0.051 bit/(s·Hz))的约48倍和16倍。并且与传统MIMO相比，尽管APC-EPA方案得到的信道容量要略低于MIMO信道容量(在SNR = 20 dB处为1.536 bit/(s·Hz))，但是APC-IPA联合方案却仍明显优于MIMO信道容量。这表明本文所提APC-IPA联合方案有效降低系统中来自非对齐和多径效应造成的干扰，提升系统信道容量，使得无线OAM-MIMO通信能够在多径和非对齐环境实现比传统MIMO更高的信道容量。此外，与文献[14]的全相位补偿法相比，尽管APC-EPA方案得到的信道容量有所减少，但减少的幅度较小，但是计算复杂度却有大幅度的降低，这对于实际通信系统是可接受的。

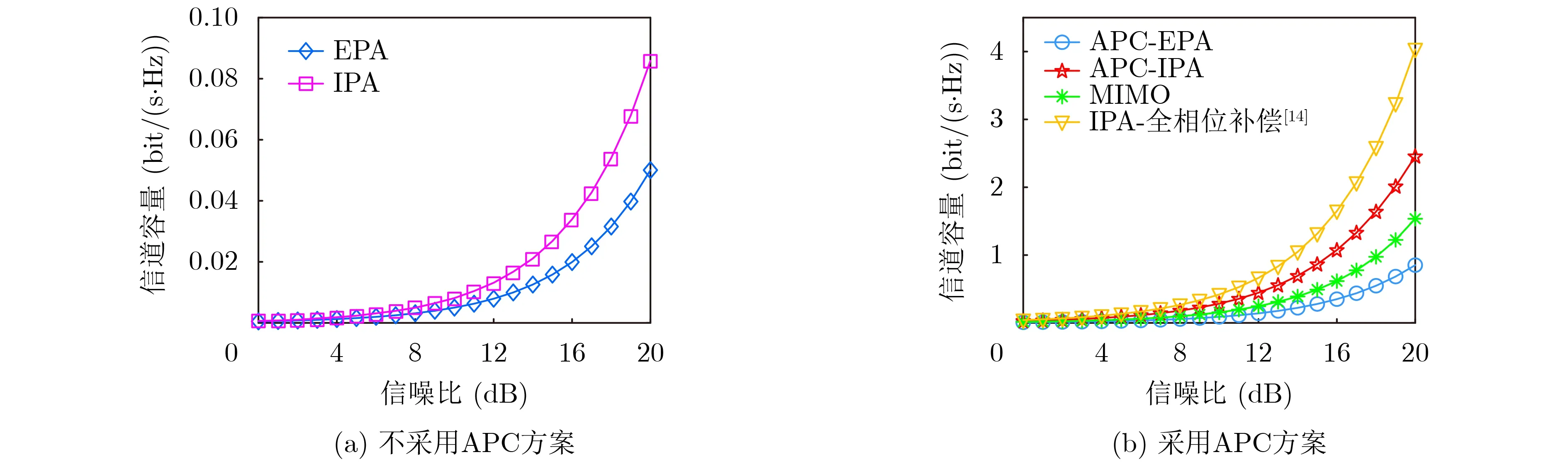
图3 不同方案下信道容量随信噪比的变化曲线

图4对比了不同OAM子信道数下IPA算法和APC-IPA联合方案的迭代次数。从图中可以看到，随着OAM子信道数的增加，两种方案的迭代次数都在增加，这是因为OAM子信道数增加代表收发天线阵列数也在增加，由此会使得信道矩阵变得更加庞大和复杂。另外还可以看到，IPA算法迭代次数增加的趋势更快，例如在OAM子信道数分别为12和36时，IPA算法的迭代次数分别是6次和12次，而APC-IPA联合方案的却只有3次和5次，这是因为在理想情况下，OAM各模态子信道的通信质量存在着较大差异，然而当遭受到来自非对齐和多径效应的干扰时，其各个子信道的通信质量和差异会大幅下降，本文所提的APC方案消除了部分来自非对齐和多径效应的相位偏差，使得各OAM模态间的干扰得到了减轻，因此，各OAM子信道的通信质量得到了提升，IPA算法的迭代次数也会降低。

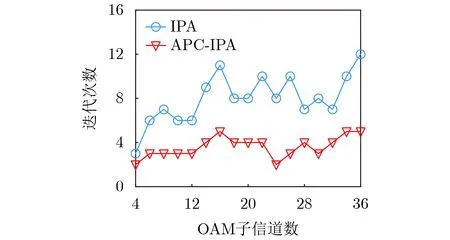
图4 算法迭代次数随OAM子信道数的变化曲线

图5比较了在LoS路径和所有反射路径下分别采用EPA方案和APC-IPA联合方案的信道容量。从图中可以看到，当采用EPA方案时，在SNR =20 dB处，LoS路径的信道容量约为0.0493 bit/(s·Hz)，是同方案下反射路径信道容量(1.35×10-4bit/(s·Hz))的约365倍；然而，当采用APC-IPA方案后，在SNR = 20 dB处，LoS路径的信道容量增加到了约0.7746 bit/(s·Hz)，反射路径的信道容量则增加到了约0.6281 bit/(s·Hz)，并且它们间的差距也减小到了约1.23倍。这是因为本文所提APC方案消除了部分来自非对齐和多径效应的相位偏差，有效减轻了系统中遭受的干扰，使得各条路径特别是反射路径的通信质量得到了大的提升，并且IPA算法还优化了功率分配方案，因此，相比于LoS路径，反射路径的信道容量会得到更大的提升。

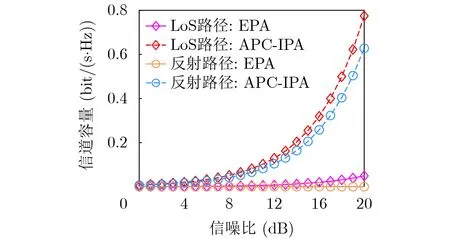
图5 LoS路径与反射路径下信道容量随信噪比的变化曲线

5 结论

本文针对无线轨道角动量通信系统在多径和收发天线非对齐场景遭受的性能损失问题，提出了一种APC-IPA联合方案。其中，APC方案不仅减轻了多径和和非对齐造成的相位偏差，也将相位补偿时的复数乘法计算次数从S × 3N降低到了3N次；IPA方案则在优化功率分配方案的同时降低了系统迭代次数。结果表明，系统性能受多径和收发天线非对齐影响较大，本文所提APC-IPA联合方案能够有效降低来自多径和非对齐不利影响，提升信道容量，如当系统SNR = 20 dB时，采用APC-IPA联合方案后，系统信道容量从0.051 bit/(s·Hz)增加到了2.461 bit/(s·Hz)，并且相比于传统MIMO系统，采用该APC-IPA联合方案后的OAM-MIMO通信有着更高的信道容量，这为无线OAM通信在实际中的应用提供了一定理论支撑。然而，该方案是在系统CSI已知的情况下实现的，并且研究也未考虑多用户、信道时变特性等问题，在下一步工作中，我们将针对上述问题，进一步完善对非理想无线OAMMIMO通信系统的研究。