复合高斯杂波条件下存在干扰时的反对称贝叶斯检测器
2022-09-22杨海峰李振兴胡晓琴狄源水
杨海峰 李振兴 胡晓琴 李 琼 狄源水
①(空军预警学院 武汉 430000)
②(93856部队 兰州 730000)
1 引言
目标检测是雷达的核心功能之一。针对高斯背景下目标导向矢量已知时的目标检测问题,Kelly[1]根据广义似然比检验(Generalized Likelihood Ratio Test, GLRT)准则推导了自适应检测器,并指出该检测器具有恒虚警率(Constant False Alarm Rate, CFAR)特性。针对高斯背景下的目标检测问题,学术界展开了深入研究[2,3]。然而随着雷达分辨力的提高和擦地角的减小,高斯杂波模型已不能较好地拟合杂波,这导致高斯杂波背景下的自适应检测器在非高斯杂波背景下的目标检测性能有一定程度的下降[4,5]。针对这个问题,人们根据实测数据提出了Weibull、对数Weibull分布、K分布以及复合高斯分布等多种杂波分布形式。其中,复合高斯分布通过相互独立的散斑分量和纹理分量的乘积来描述杂波。通过合理设置纹理分量,复合高斯模型可包含Weibull分布、对数Weibull分布和K分布等多种分布形式[6-8]。因此,复合高斯背景下多通道雷达自适应检测问题已经成为一个研究的热点问题。
日益复杂的战场电磁环境使得雷达必须面对各种有意或无意干扰,但目前大部分针对高斯背景下存在干扰的问题进行研究[9-12],对于复合高斯背景下存在干扰时的自适应检测器也有一定研究[13]。此外,自适应检测需要足够多独立同分布(Independent Identically Distributed, IID)的训练样本才能保证较好的目标检测性能[14],而干扰的存在会导致IID训练样本更加难以获取。为解决样本数不足的问题,文献[15, 16]通过假设杂波协方差矩阵服从逆威沙特分布,然后利用贝叶斯准则得到贝叶斯检测器,可有效提高训练样本数不足时检测器的性能,但当先验信息存在误差时贝叶斯检测器的性能会有较大的下降。此外,文献[17-20]基于杂波协方差矩阵的反对称特性,推导了高斯背景下存在干扰时的反对称检测器,可有效提高训练样本数较少时的检测性能。但反对称检测器要求训练样本数为系统自由度的一半以上才能适用。为了进一步提高检测器在复合高斯背景下存在干扰且训练样本很少时的性能,本文同时利用杂波协方差矩阵先验信息和反对称特性设计检测器,可有效提高检测器在训练样本严重不足时的检测器性能。此外,通过利用杂波协方差矩阵反对称特性,也可有效改善先验信息不准确时的目标检测性能。
本文结构如下:第2节给出了该问题的信号模型,第3节根据贝叶斯准则和反对称特性推导了该模型下的自适应检测器,并在随后的第4节利用仿真验证了本文提出的检测器的有效性,最后在第5节对全文进行了总结。
2 信号模型

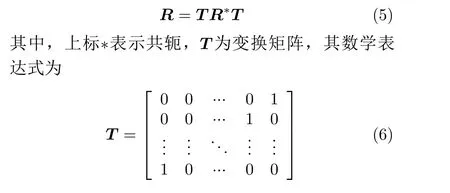
3 检测器设计

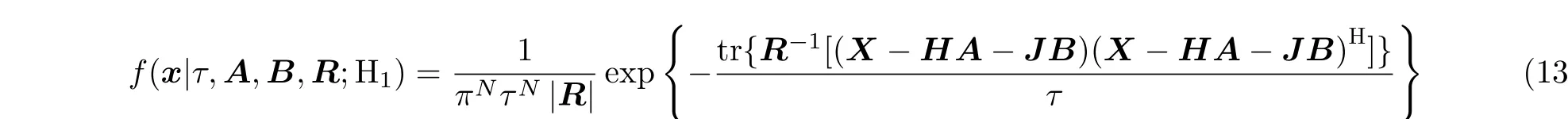



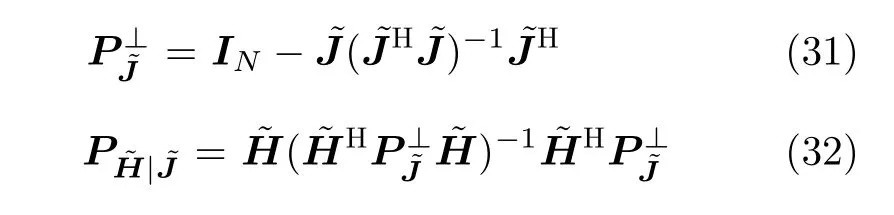
4 仿真分析
复高斯杂波的协方差矩阵建模为具有单一滞后相关系数的指数相关随机向量,即R的第(i,j)个元素 为ε|i-j|,i,j=1,2,...,N。令N=15 ,ε= 0.9,τ服从逆伽马分布,且形状参数和尺度参数均设置为2。考虑到计算量的限制,本文虚警概率设置为10-3,检测概率和检测门限均通过105次蒙特卡罗仿真得到。信号子空间H和干扰子空间J随机选择,选定后就不再变化。假设信号坐标向量a和干扰坐

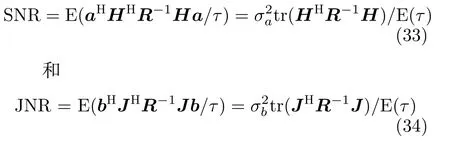
为比较本文检测器的性能,本文将文献[4]中的检测器反对称检测器进行扩展,使其能应用于干扰环境下,其检测器具体形式为

其中,R¯ 为式(2)引入的先验信息,并用“Bayes”在结果中显示。此外,本文进一步给出了杂波协方差矩阵已知时的检测器作为性能基准,用“Idea”在仿真结果中显示。为不失一般性,本文将杂波协方差矩阵先验分布的均值R¯设置为单位阵,在实际情况中通过合理设置R¯可进一步提高检测器性能。此外,杂波协方差矩阵计算中的初始值也设置为单位阵。
从图1可以看出,本文提出的检测器在样本数很少的时候就具有较好的检测性能,且检测性能随着训练样本数的增加而上升,而贝叶斯检测器由于只利用了杂波协方差矩阵的先验信息,没有利用训练样本,因此其检测性能没有随着训练样本数的增加而变化。此外,由于训练样本数很少,此时反对称检测器失效。当样本数进一步增加时,本文提出的检测器的检测性能进一步提升,同时反对称检测器生效,且检测性能随样本数增加而上升,如图2所示。但在样本数不够多时,本文检测器的检测性能强于反对称检测器的检测性能,如图2(a)。而当样本数较多时,本文提出的检测器和反对称检测器的性能接近一致,如图2(b)。此外,由于贝叶斯检测器没有利用训练样本,因此其检测性能不受训练样本数的影响,故在图2没有给出贝叶斯检测器的检测性能曲线。

图1 µ r=16, JNR=30 dB不同检测器的检测概率曲线
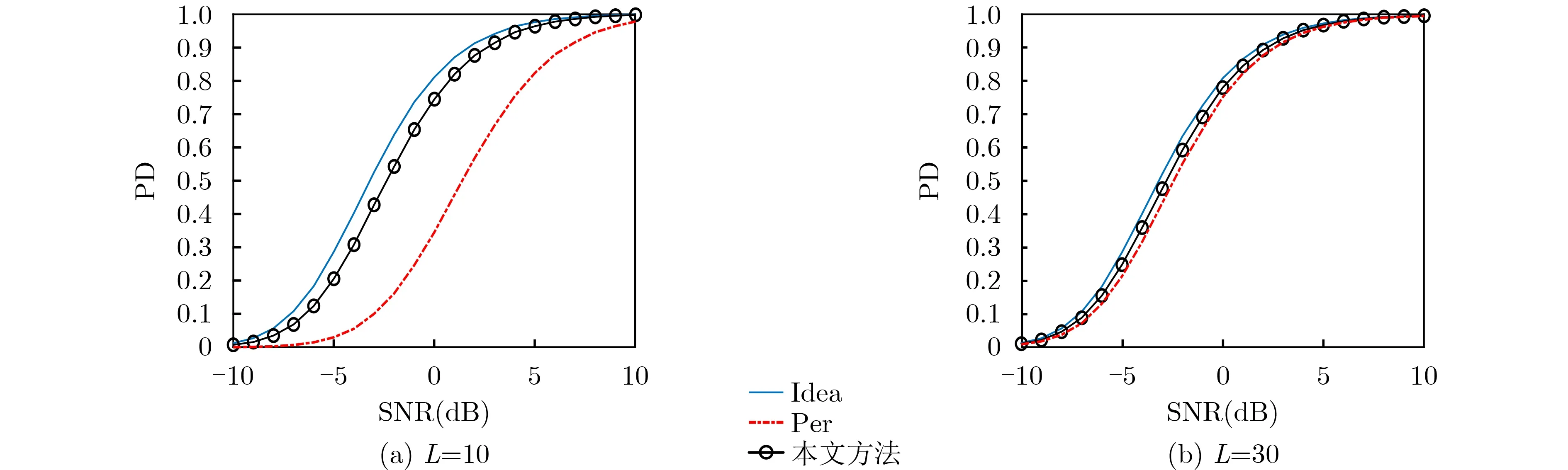
图2 µ r=16, JNR=30 dB不同检测器的检测概率曲线
对比图1和图3,可看出当样本数相同时,随着µr的增加,本文提出的检测器的检测性能有一定的下降,原因是µr决定了先验信息在检测器中的重要程度。由于协方差矩阵先验信息与实际的协方差矩阵存在差异,因此当µr增加时,检测器的性能有一定的下降。
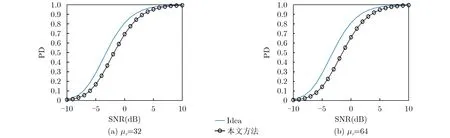
图3 L=5, JNR=30 dB不同检测器的检测概率曲线
从图4可以看出,本文提出的检测器的检测性能不受干扰强度变化的影响,这说明本文提出的检测器可完全抑制干扰。

图4 L=5, µ r=17, SNR=1 dB不同检测器的检测概率曲线
通过合理设置纹理分量,复合高斯模型可变换对数Weibull分布和K分布等多种分布形式[6-8],图5给出了不同杂波分布条件下的检测性能曲线。从图5可以看出,虽然在不同杂分布条件下,本文检测器的检测性能有一定的差异,但其仍保持较好的检测性能。
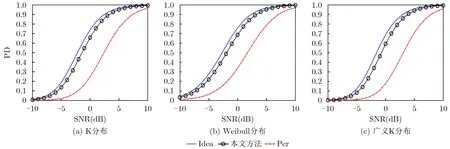
图5 L=10不同检测器不同杂波分布下的检测概率曲线
5 结论
本文针对复合高斯背景下存在干扰时的目标检测问题进行研究。根据接收阵列天线的对称特性和贝叶斯定理,基于两步GLRT推导了该条件下的自适应检测器。仿真结果表明,在干扰子空间已知的条件下,本文提出的检测器可有效抑制干扰,且在样本数量较少的情况下检测性能优于常规的反对称自适应检测器。
