合成孔径无源定位性能分析与参数设计

王裕旗 孙光才 邢孟道 张子敬

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

1 引 言

在无源电子侦察中，单站辐射源精确定位对于目标精确识别、干扰和打击具有重要的意义[1-4]。传统电子侦察设备主要通过测角进行定位[5,6]，测角定位的方位分辨能力会随着距离的增加而下降。通过平台的运动，可以实现多个位置测角联合定位[7-9]，也可以通过平台运动过程中测量侦察信号的多普勒或多普勒的变化率完成辐射源的定位[10,11]。Weiss[12]在2004年提出了直接定位法(Direct Position Determination, DPD)，通过构建与辐射源位置相关的目标函数搜索信号源的位置。直接定位技术自提出以来，受到了国内外广泛的研究[13-28]。

DPD问题主要可以分为两类。一类DPD问题是基于阵列天线的空间谱估计问题[13-33]，估计方法分为最大似然估计(Maximum Likelihood Estimation,MLE)法和高分辨谱估计法(多信号分类(MUltiple SIgnal Classification, MUSIC)、Capon等)。信号源的位置决定了不同基站接收信号的导向矢量，最大似然类的算法构造与信号源位置直接相关的导向矢量，通过最小二乘的方法实现信号源的定位[13-17]。高分辨谱估计类的算法将DPD问题和MUSIC, Capon的方法结合，通过子空间的方法，获得高分辨的直接定位空间谱[18-22]。另一类DPD问题是基于时差频差的多站DPD问题[23-28]。信号源的位置决定了发射信号在不同基站的到达时间，在基站运动的情况下，信号源的位置同时决定了不同基站接收信号的达到时间和多普勒频率。通过最大似然的方法，补偿接收信号的到达时间和多普勒频率，完成信号源的定位。DPD定位方法需要阵列天线或多个接收站，在处理方法方面，对于不同时刻接收的信号，DPD实现信号的非相参叠加。

合成孔径雷达(Synthetic Aperture Radar,SAR)是一种高分辨成像雷达，在探测与侦察中应用广泛[29-32]。雷达载体沿方位向飞行过程中，接收信号形成合成阵列，通过方位聚焦获得高的方位分辨率。合成孔径无源定位采用了合成孔径成像的工作方式，只需要利用单个接收天线，通过运动形成虚拟孔径，利用合成孔径技术，获得信号源的位置。合成孔径无源定位利用斜距历程中2次调频率和辐射源距离的函数关系，构造聚焦核函数进行距离搜索，获得信号源的距离位置，通过方位聚焦的结果获得方位位置[33]。合成孔径定位方法补偿了发射的基带信号和不同接收时刻的初始相位，实现接收信号的相参积累，获得了很高的信号增益。在低信噪比的情况下，合成孔径定位方法可以获得更好的定位效果。

无源定位中的波束宽度远大于SAR成像的波束宽度，通过合成孔径技术进行无源定位时，合成孔径的长度是重要的参数。过长的孔径长度使斜距历程的多项式近似产生误差，从而带来距离定位的误差，过短的孔径长度会使两维分辨率下降，从而影响定位的精度。针对合成孔径无源定位中孔径长度的优选问题，本文从合成孔径定位的原理出发，分析了精确的聚焦表达式，给出了定位误差估计核函数，并给出了工程应用中近似的解。通过2维分辨率分析，给出了2维分辨率的表达式。在此基础上，综合考虑定位精度和分辨率的需求，给出了合成孔径长度的优选方法。最后通过仿真对理论分析进行了验证。

2 合成孔径无源定位模型误差分析

式(8)为2次项定位的误差分析函数。图1为距离向的聚焦位置偏差，图2为式(8)的理论分析结果。

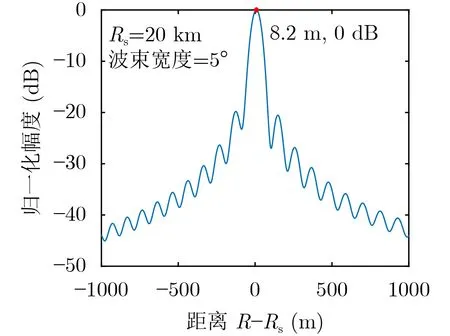
图1 聚焦位置偏差

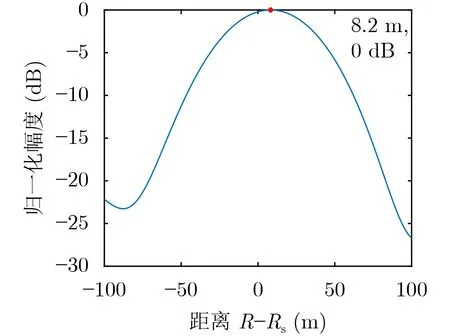
图2 误差的理论分析结果

3 合成孔径无源定位分辨率分析

合成孔径定位的主要优势是其实现信号的相干积累，且具有很高的方位分辨率。其方位分辨率和SAR成像的方位分辨率相同，和信号的方位带宽有关，其距离分辨率和SAR的分辨率有所区别，因此本节主要对其距离分辨率进行详细分析。

3.1 方位分辨率

3.2 距离分辨率

以单频信号为例，在2次近似的情况下，认为

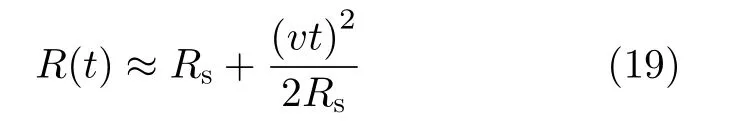
根据误差分析的部分，在波束宽度限制范围内，忽略4次以上的相位，在-3 dB处的聚焦效果为

4 线性合成孔径长度L的优化

距离分辨率决定的L(ρr)可以通过数值计算的方法，获得合成孔径长度和距离分辨率的对应曲线ρr(L)，通过此曲线确定L(ρr)。

5 仿真及性能分析

5.1 定位误差随距离和波束宽度的变化

合成孔径的长度固定为3490 m，波长为0.1 m，通过式(8)可以得到定位误差随距离的变化情况，如图3所示。固定孔径长度的情况下，高次项引起的定位误差随着距离的增加而减小，定位误差和距离呈反比的关系。当合成孔径长度固定时，远距离会使高次项的影响减小，从而定位误差更小。

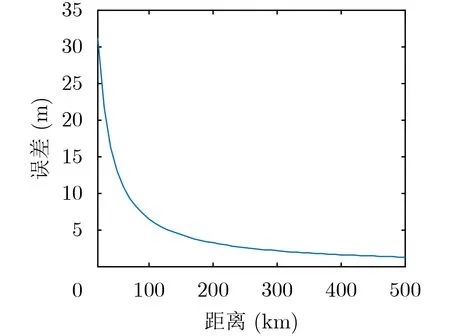
图3 定位误差随距离变化情况图

当合成孔径长度为一个波束照射的宽度时，在不同的距离处，定位误差和波束宽度的关系如图4所示。从仿真结果可以看出，高次项引起的定位误差为近似为孔径长度的2次函数的形式，并且同样波束宽度情况下的定位误差随着距离的增大而增加。

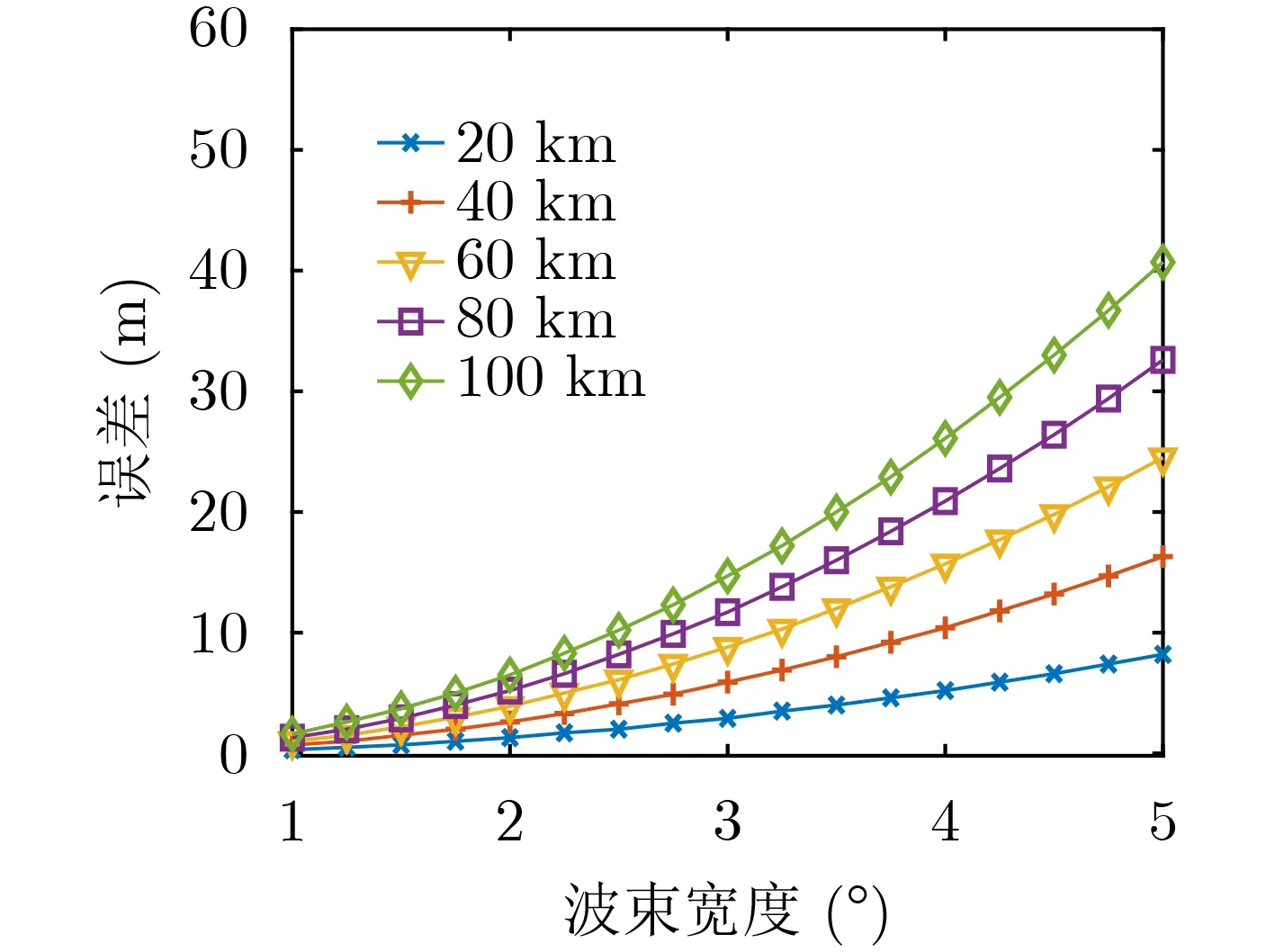
图4 定位误差随波束宽度变化情况

5.2 定位误差近似解

不同距离满足合成孔径成像中2次项匹配假设的波束宽度为

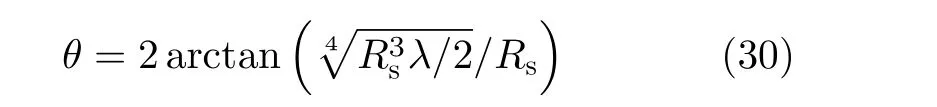
表1给出了几组不同距离，2次匹配的假设条件下的波束宽度限制。

表1 不同距离的波束宽度限制

在满足式(30)给出的波束宽度限制的条件下，本节给出通过近似计算的定位误差和通过仿真得到的定位误差的差值，在2次项匹配假设的波束宽度限制范围内，近似分析和理论值的误差趋于0，如图5所示。

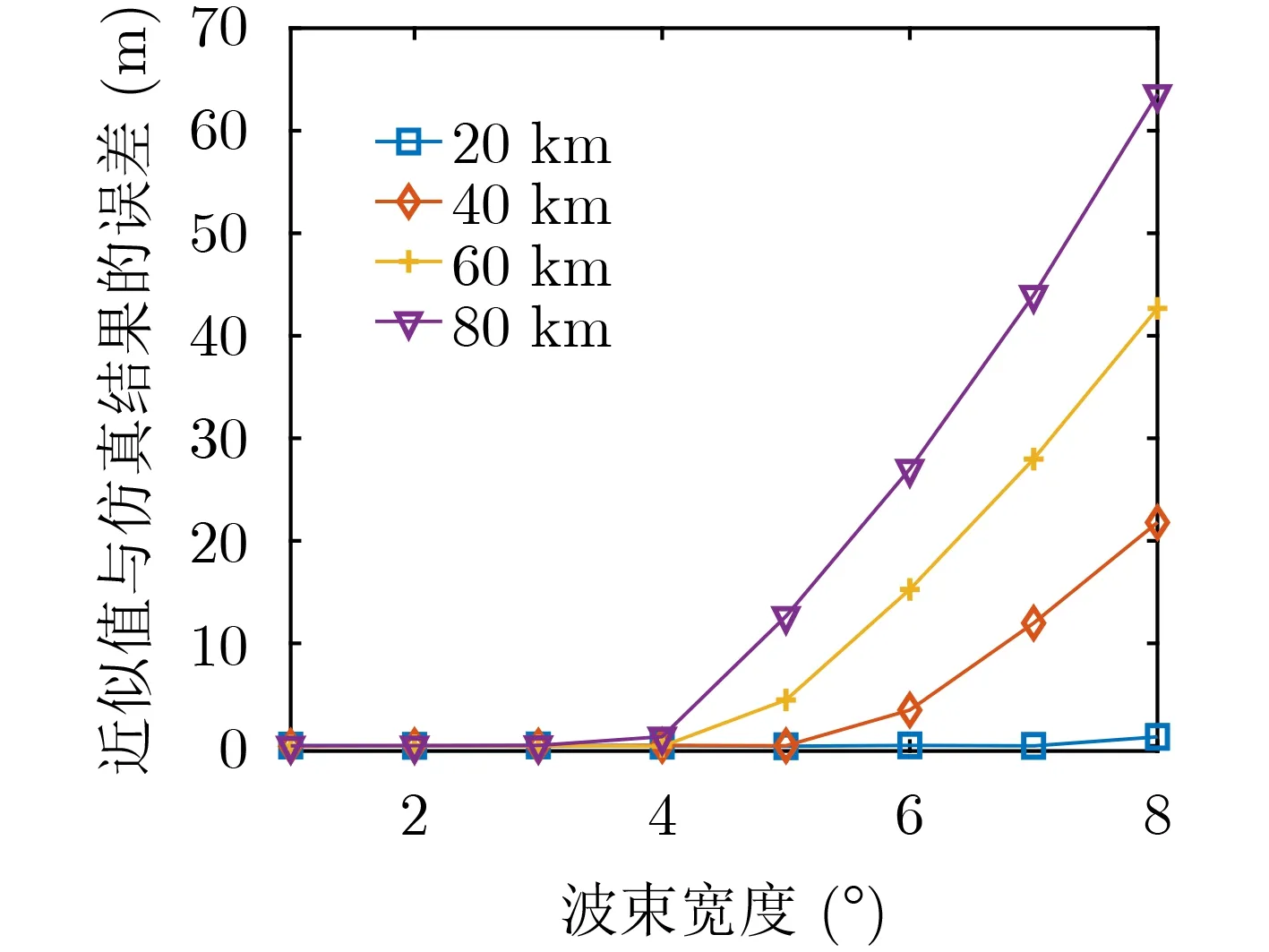
图5 定位误差近似分析结果图

5.3 分辨率分析

信号源的距离为20 km，载机的速度为100 m/s，合成孔径长度为1048 m，波长为0.1 m时，距离分辨率分析的仿真和理论分析结果如图6所示，仿真分析得到的距离分辨率为252.8 m，通过Fresnel积分计算的理论结果为252.8 m。从分辨率分析的结果可以看出，距离分辨率不以中心点Rs对称，在近距离处的分辨率略高于远距离处的分辨率。

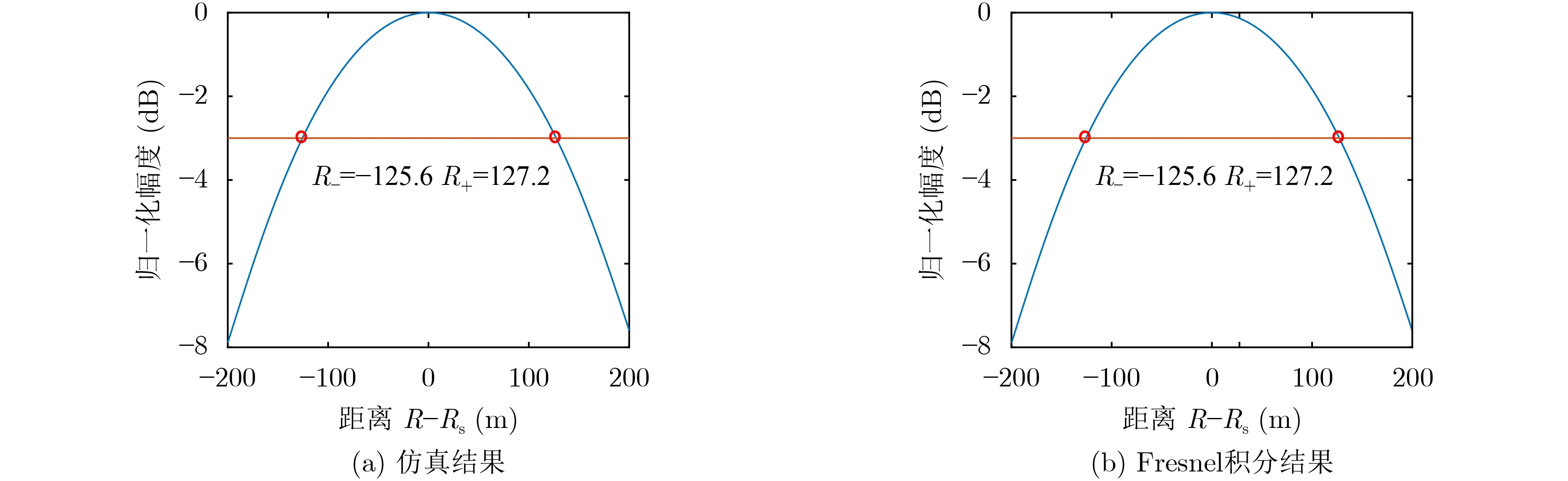
图6 距离分辨率分析结果

方位分辨率的仿真结果如图7所示，方位分辨率为1.69 m，通过式(17)计算的理论分辨率为1.69 m。仿真和分析结果可以看出，方位分辨率明显高于距离分辨率。

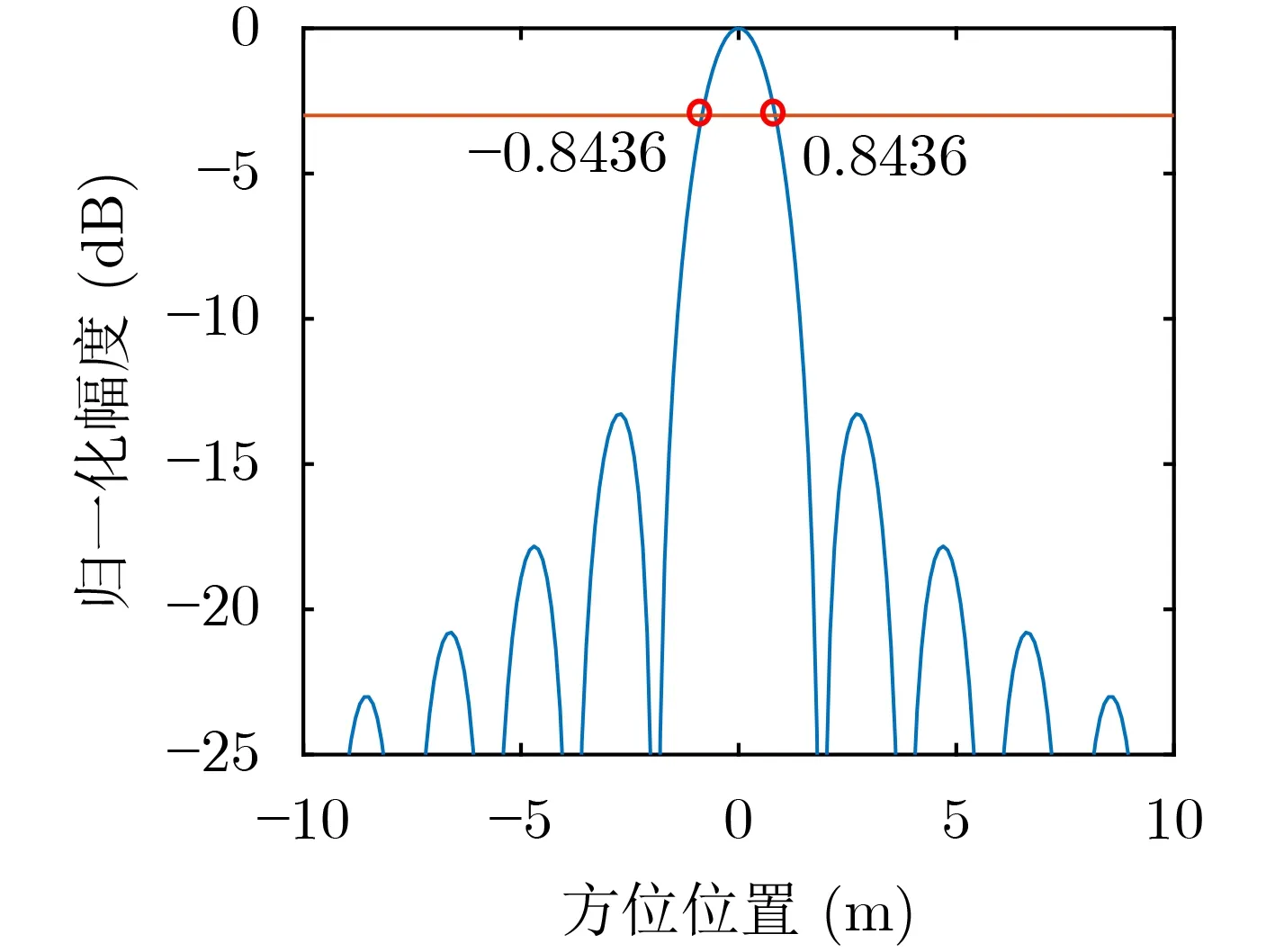
图7 方位分辨率分析结果

5.4 线性合成孔径长度的优选

合成孔径长度的优选主要考虑定位误差和分辨率两个因素，由分辨率分析的结果可知方位分辨率远小于距离分辨率，因此在优化合成孔径长度时，可以只考虑距离分辨率的影响。

首先由定位误差可以得到孔径长度的上限。仿真中设定不同的定位误差的阈值δ为1 m, 3 m, 5 m和10 m，最大合成孔径长度随距离变化的情况如图8所示。然后由分辨率要求可以得到孔径长度的下限。仿真中设定不同的分辨率要求ρr为150 m, 200 m,250 m和300 m，最小合成孔径长度随距离变化的情况如图9所示。

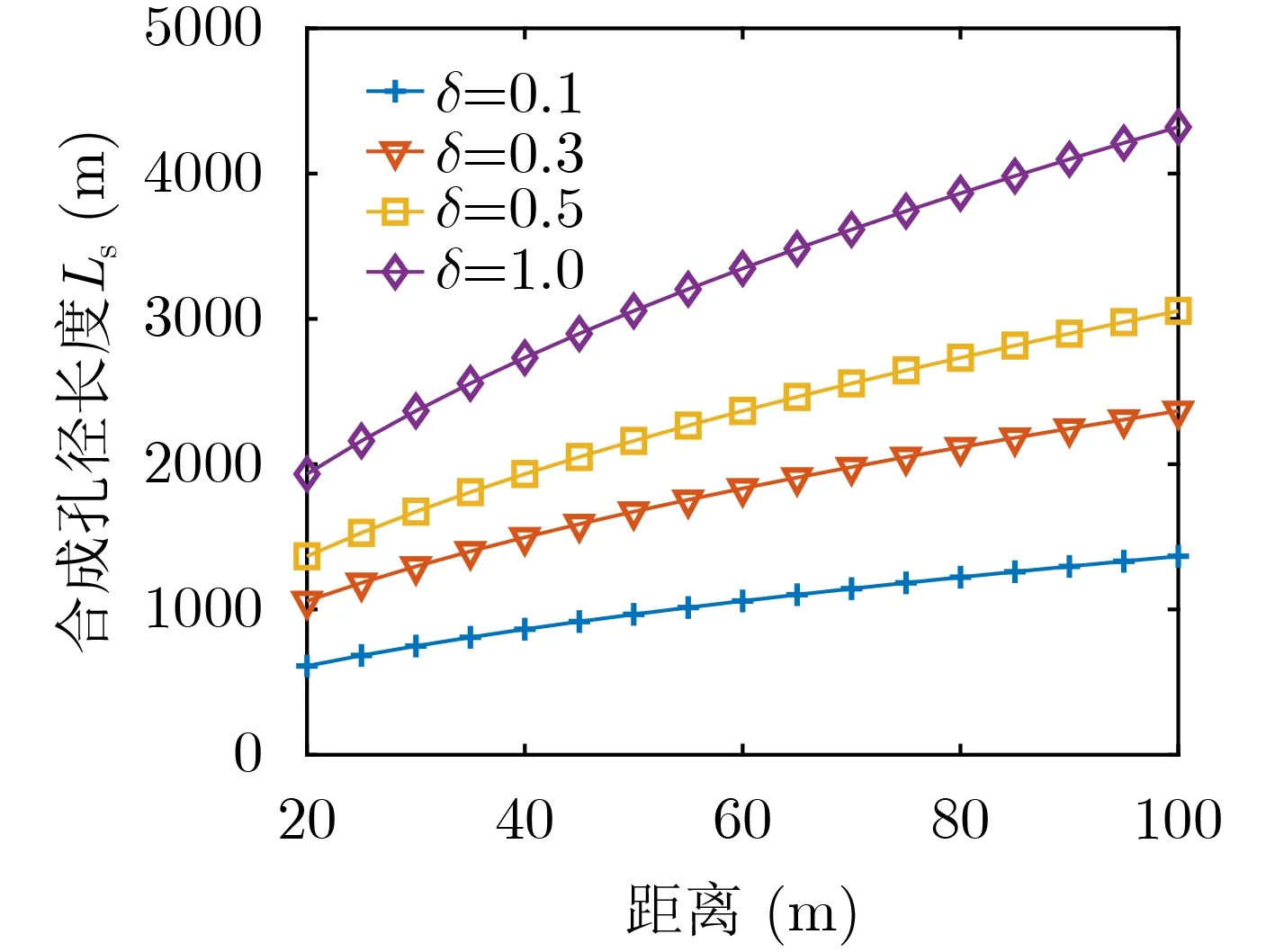
图8 合成孔径长度上限随距离变化图

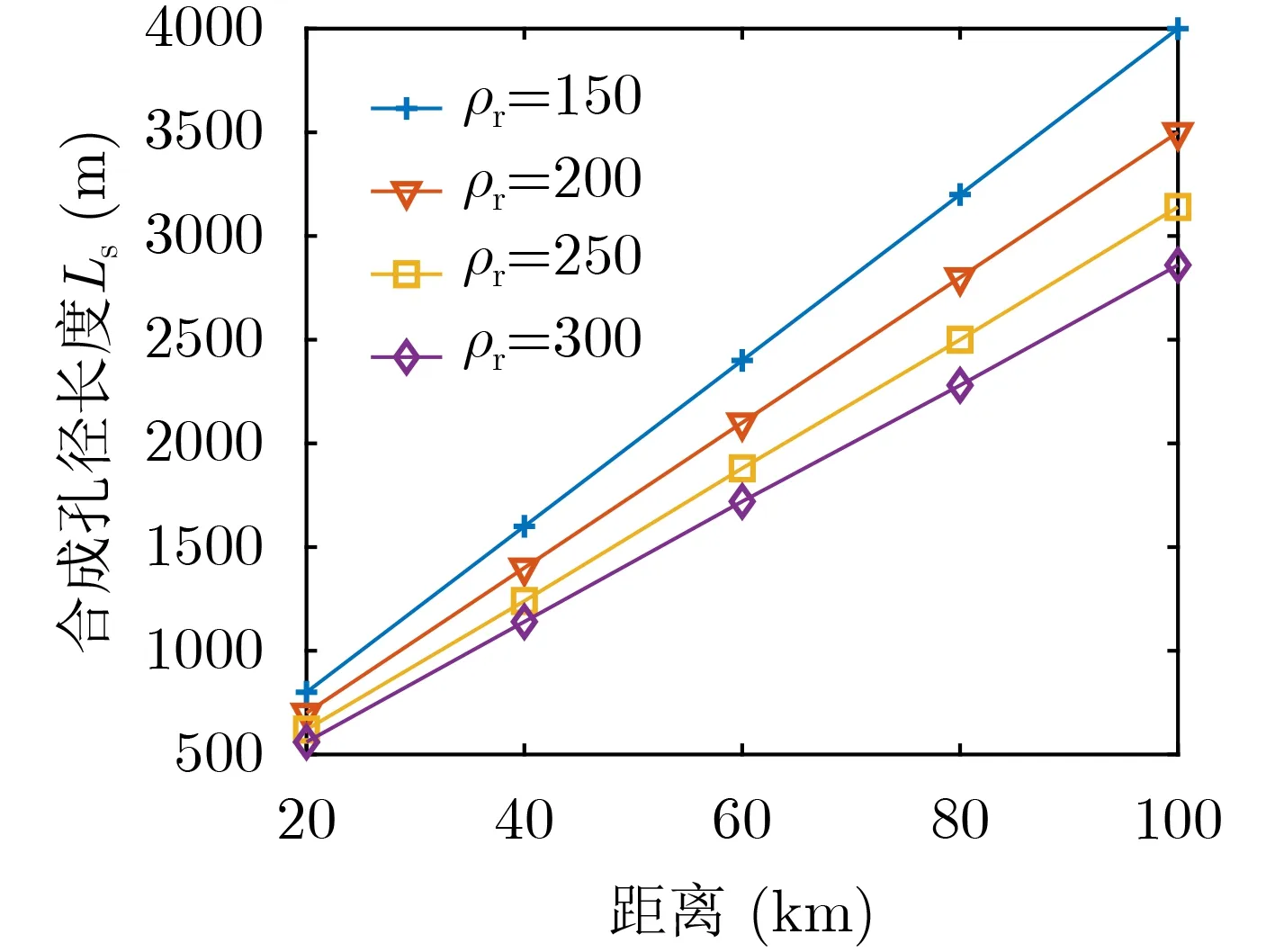
图9 合成孔径长度下限随距离变化

合成孔径长度的可选范围为合成孔径长度上下限之间，当给定定位误差和分辨率的要求时，可以获得上下限随距离的曲线。给定定位误差为5 m，距离分辨率300 m，上下限曲线如图10所示，随着距离增大，可选长度的区间逐渐减小。仿真结果表明距离越近，上下限的约束更宽松，对于近距离的信号源目标，可以在满足精度要求的前提下，设置尽量长的孔径长度，从而获得更高的定位精度。

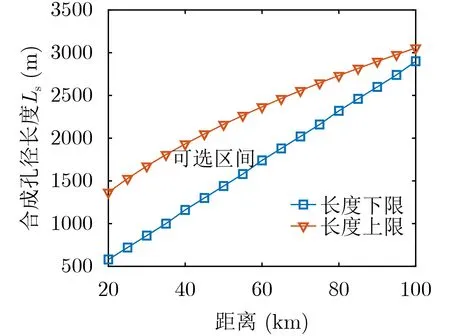
图10 合成孔径长度优选曲线

6 结束语

合成孔径无源定位中，定位的距离误差主要来源于高次项的影响，通过2次项匹配定位时，高次相位不可忽略，在偏离目标距离处的匹配函数使信号的聚焦效果最优，因此导致距离定位的误差。本文通过不同距离处匹配聚焦的函数，分析了误差的影响因素，给出了工程上近似分析的结果，在此基础上给出了合成孔径长度的上限。定位的分辨率和合成孔径的长度有关，通过分析距离和方位2维分辨率，结合分辨率的需求，给出了合成孔径长度参数设计的下限。通过本文的研究，可以根据定位误差的容忍程度和定位分辨率的需求，确定合成的孔径长度，从而获得更好的定位效果。