基于随机几何理论的多天线密集异构网络性能分析与优化
2022-09-22赵东来刘浩洋贾少波
赵东来 王 钢* 刘浩洋 贾少波
①(哈尔滨工业大学电子信息与工程学院 哈尔滨 150001)
②(郑州大学信息工程学院 郑州 450000)
1 引言
随着智能手机、可穿戴设备、物联设备等智能终端的普及以及高清视频、虚拟现实等新型业务的兴起,移动网络中的数据流量呈爆炸式增长[1,2]。传统网络已无法满足大量用户对高速、低时延无线业务的需求,而密集异构网络技术通过在宏小区覆盖范围内密集部署低功耗的小基站,实现了提高系统吞吐量、消除盲点、热点增强的目的[3,4]。因此,异构网络融合技术将在6G时代得到更广泛的应用。但多种类型基站的灵活、密集分布使得网络结构复杂化,采用多天线技术也使得干扰情况进一步复杂化。这都为系统的性能评估和分析增加了难度[5,6]。对系统性能的准确计算和有效分析是系统参数设计、性能优化的基础。因此,推导出关键性能指标准确、低复杂度的表达式是多天线密集异构网络需要迫切解决的问题。
Andrews等人[7]首次将随机几何模型引入到无线移动网络,将基站和用户的分布建模为齐次泊松点过程 (Homogeneous Poisson Point Process,HPPP),构造了一个普适的信干噪比(Signal-to-Interference-plus-Noise Ratio, SINR)统计分析框架,并推导出单层蜂窝网络覆盖率和遍历速率的闭合表达式。通过与实际网络仿真结果对比,验证了基于随机几何模型进行性能分析的准确性。此后,随机几何理论作为一种分析工具被广泛应用到无线网络中。文献[8]将文献[7]的研究成果扩展到多层异构网络,分析了在开放和闭合两种接入模式下的覆盖率性能。文献[9]研究了接入偏置因子对网络中断概率和遍历速率的影响。文献[10]分析了多层密集异构网络在Nakagami-m衰落信道下的覆盖率和频谱效率,并根据推导出的渐进表达式设计了SINR门限优化算法,使得在满足覆盖率需求的前提下最大化频谱效率。一种适用于缓存超密集网络的多请求用户关联策略在文献[11]中被提出,作者通过理论分析证明了这一策略可改善覆盖率,提高缓存命中率。文献[12]针对一种室内开放场景,例如飞机场、大型展厅及火车站,设计了基站部署方案。研究结果表明在此场景中即使密集部署规则分布的室内基站也可获得性能增益。贾向东等人[13]设计了基于无人机(Unmanned Aerial Vehicle, UAV)辅助的异构网络,将UAV建模为泊松簇过程(Poisson Cluster Process, PCP),利用随机几何理论推导了地面用户的覆盖率表达式,并进一步分析了UAV的高度及平均簇内成员数对覆盖率的影响。
以上研究成果都是采用单天线模型,即基站和用户都假设为单天线。众所周知,多天线技术可以带来诸多益处,例如复用增益及分集增益[14]。文献[15]分析了天线数对密集小小区网络关键性能指标的影响,仿真结果表明增加基站天线数可以指数级降低中断概率,从而始终提高网络吞吐量。利用矩量母函数(Moment Generating Function,MGF),文献[16,17]推导了多天线异构系统的覆盖率积分表达式,由于需要计算多重积分,复杂度很高。基于文献[8,9]的研究结果,文献[18]通过为宏基站配置大规模天线提高了异构网络速率和覆盖率,但由于微基站为单天线,宏基站天线数的增加会使得各层间负载不均衡。以上多天线场景中仅基站配置了多天线,用户侧仍假设是单天线,而实际的智能终端普遍采用了多天线,因此这一假设过于简单。此外,针对多天线多层异构网络的研究成果中均未给出覆盖率等性能指标的闭合表达式,本文提出一种适用于多天线密集异构网络的性能分析框架,其中基站和用户构成多输入多输出 (Multiple-Input Multiple-Output, MIMO)系统,主要研究成果包括:
(1)推导了覆盖率的闭合表达式和区域频谱效率(Area Spectral Efficiency, ASE)的积分表达式,并给出了相应的优化方案。还推导了复杂度较低的覆盖率渐进表达式和ASE上界。
(2)提出一种有效的算法来设计最优的基站密度,以在满足覆盖率需求的前提下最大化ASE。
2 系统模型
2.1 密集异构网络模型
考虑一个K层密集异构网络,第k(1≤k ≤K)层基站配置Mk根 天线且发射功率为Pk。每层基站的分布建模为相互独立的密度为λk的 HPPPΦk。同样,用户的分布建模为密度为λu的独立HPPPΦu。每个用户都配置了N根天线,假设Mk ≥N。每个基站共用相同的频谱,即频率复用因子为1。在每个时隙,每个基站仅服务1个用户。一个3层密集异构网络模型见图1,为了清晰简洁,图1中未画出干扰链路。

图1 密集异构网络系统模型
采用基于长时平均接收功率的小区关联规则[9],这意味着用户将在满足式(1)时连接到第k层


利用MIMO技术,可同时获得分集增益和复用增益。假设基站可获得完美的信道状态信息且基站采用迫零预编码。同时假设信道状态矩阵满秩,则利用空间复用技术,在下行链路基站可同时向用户传输N路数据流。利用HPPP的移不变性,将所研究的一个典型用户位置设为欧氏平面的原点。用户不但会接收到来自服务基站的通信信号,还会收到来自同层和跨层基站的干扰信号。若此典型用户连接到第k层位于x0处的基站,则其第n根天线的SINR可表示为

2.2 性能指标


3 覆盖率性能分析及优化
3.1 覆盖率闭合表达式



基于覆盖率的闭合表达式可分析基站密度、发射功率、天线数等系统参数对覆盖率的影响,并设计覆盖率的优化方案。由式(20)可知:
(1)覆盖率是关于基站天线数的增函数,这是因为较大的发射天线数会增加分集增益。因此,为了优化系统的覆盖率性能应该尽可能为基站配置较多的天线。


可见为了最大化覆盖率只需要激活具有最大天线数网络层的基站,并关闭其他层的基站。显然只激活部分基站会降低系统ASE,关于ASE的优化将在第4节进行讨论。
尽管通过定理1和式(20)获得了覆盖率的闭合表达式,但其形式仍然有些复杂。为了简化结构以直观地观察系统参数对性能的影响,下一节给出了一种渐进的表达式。
3.2 覆盖率渐进表达式

4 ASE性能分析及优化
为了求得ASE的精确值,本节首先推导了ASE的积分表达式。为了减少积分运算的复杂度,随后给出了一种ASE的上界闭合表达式,并以此设计了一种ASE优化算法。
4.1 ASE表达式
定理3 系统ASE的精确值可由式(27)求得

将式(29)代入式(27)可得式(28)。 证毕
无论是采用精确的积分表达式还是上界表达式,均可知ASE随基站密度线性增加,因此为了最大化ASE需要激活系统中的所有基站。但由上节分析可知,为了最大化覆盖率只需要激活具有最大天线数的基站,所以ASE和覆盖率不能同时取得最大值,系统设计需要在二者间进行折中。
4.2 ASE优化算法
本文将在满足覆盖率需求的前提下,最大化ASE,相应的优化问题可表示为


5 数值结果与分析
本节给出了由MATLAB 2016b得到的数值仿真结果以验证上文的理论分析结果。考虑一个由宏基站和微基站组成的典型两层异构网络,整个网络共享10 MHz的频带,高斯白噪声的功率为-104 dBm,宏基站发射功率P1=20 W,微基站发射功率P2=2 W,路径损耗指数α=4,其他系统参数见各图标题。仿真结果采用蒙特卡罗方法,每个仿真点共进行105次实验。各层基站泊松分布在一个2 km×2 km大小的网络区域内,典型用户位于2维平面的原点。

表1 最优基站部署方案求解算法(算法1)
图2对比分析了由定理1获得的覆盖率理论值、定理2的渐近值和仿真值,其中,[λ1,λ2]=[1,5]×102/km2, [M1,M2]=[4,2]。如图2所示,理论值和仿真值完全吻合,验证了前文推导的覆盖率闭合表达式的精确性,也验证了系统是干扰受限的。渐近值随着SINR门限的增大而逐渐与理论值吻合,且可观察到渐近值是理论值的一种上界。覆盖率随着SINR门限的增加而减小,与覆盖率的定义相符。此外,当用户天线数减小时,覆盖率反而增大了,这是因为较小的用户天线数可以获得较大的分集增益。图3给出了基站密度对覆盖率的影响,其中,λ1=1×102/km2,β=0dB,N=2。由图3可知,当各层基站的天线数相同时,安装更多的微基站不能提高网络覆盖率。当微基站的天线数大于宏基站时,覆盖率随微基站密度的增加而增加,否则,微基站密度的增加会减低覆盖率。因此,为了改善网络覆盖率,新建站应该配置尽量多的天线。
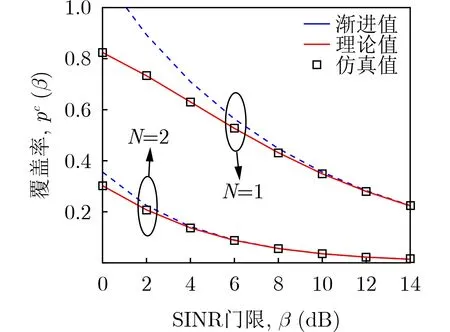
图2 覆盖率对比分析
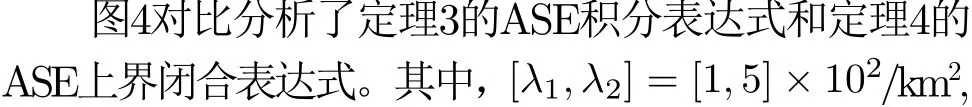

图3 基站密度对覆盖率的影响

图4 ASE精确值与上界


图5 最优激活态基站密度
6 结束语
本文提出一种适用于多天线密集异构网络的性能分析框架。通过将各层基站和用户的位置建模为HPPPs,推导了覆盖率的闭合表达式和ASE的积分表达式,为系统的性能评估提供了理论依据。为了降低计算复杂度,还给出了覆盖率的渐进表达式和ASE的上界,并进一步分析了系统关键参数对性能指标的影响。当每层基站具有相同的天线数时,覆盖率与基站密度和发射功率无关,即SINR的统计不变性仍然成立。为了提高覆盖率,最好安装或激活天线数较多的基站,这样可以带来较大的分集增益和阵列增益。此外,利用本文提出的算法1可以在满足覆盖率需求的前提下,最大化ASE并求得相应的最优基站部署密度。本文的分析结果可以推广到多用户或大规模MIMO场景,这也是下一步的研究重点。
