基于TDOA/FDOA相位条纹的高精度GPS信号跟踪方法
2022-09-22王兆瑞李建斌金声震
王 芮 王兆瑞 李建斌 金声震
①(中国科学院国家天文台 北京 100101)
②(中国科学院大学天文与空间科学学院 北京 100049)
1 引言
全球定位系统(Global Positing System, GPS)信号跟踪的目的有两个,一个是实现对卫星导航信号中伪码分量的跟踪,另一个是实现对载波分量的跟踪。传统接收机的码跟踪采用延时锁定环(Delay Locked Loop, DLL),在接收机的I, Q支路上,利用本地码发生器产生相位超前和滞后的4路信号,与接收信号做相关,比较计算结果以获得码相位误差来控制码的数字控制振荡器(Numerically Controlled Oscillator, NCO)产生与接收码相位一致的本地信号[1]。这样得到的伪距时延能精确到1%码片内,伪距测量误差大约3 m[2]。为得到更高精度的伪距测量值,国内外学者提出了诸多改善码跟踪环性能的方法。文献[3]以相关峰值点为分界点对相关峰两侧分别做最小二乘拟合,以两直线交点的横坐标与零相偏参考值的差值作为码相位的估值,以此提高精度但测量范围有限,仅适合码相位误差在一个采样点内的测量;文献[4]改进了码鉴别器,用归一化超前减滞后的功率包络型算法,有效提高了鉴相线性范围和牵引范围,但环路结构并没有得到简化;文献[5]以计算互功率相位谱的条纹频率来测量码相位,环路所需相关器减少,但在噪声较大时相位谱数据质量差,要以更长的信号时间为代价来提高鉴相精度;文献[6]在低采样率情况下,以增加热噪声为代价实现有限带宽内的码相位测量;文献[7]提出了多径干扰下的无失真码跟踪算法,不仅能抑制干扰,同时能实现码相位的无偏估计。
载波跟踪的关键技术是恢复出与载波同频的相干载波,典型的载波跟踪环由一个频率或相位鉴别器、环路滤波器和载波NCO组成。无论是锁频环(Frequency Locked Loop, FLL)还是锁相环(Phase Locked Loop, PLL),它们的环路带宽都是固定的。当多普勒动态变化较大时,无法实现频率的稳定跟踪[8]。为此,国内外学者对改进载波跟踪技术提出了诸多方法,对环路结构中的鉴频器和环路滤波器进行优化,以扩宽线性鉴频范围,减小鉴频误差[9];文献[10]设计了一种基于锁频环和锁相环的混合载波跟踪环路,环路可根据噪声环境变化自动切换工作模式,改善了环路状态转换过渡中出现频率阶跃的问题;文献[11]用平方法和差分法分别构造新的相干累加变量作为FFT运算的输入,提升了在弱信号下的频率牵引速率;将最大似然估计(Maximum Likelihood Estimation, MLE)、扩展卡尔曼滤波(Extend Kalman Filter, EKF)、无迹卡尔曼滤波(Unscented Kalman Filter, UKF)和叉积自动频率控制(Cross-Product Automatic Frequency Control, CPAFC)等自适应技术引入到载波跟踪算法,使载波跟踪环的噪声带宽根据不同的动态环境自动调节,不同程度上提高了环路的动态跟踪性能,但同时也增加了算法的复杂度[12-15]。以上方法本质上都是在I, Q支路上使用数学统计规律对状态量进行一定条件下的最优估计,鲜有学者采用统一的算法实现载波多普勒与伪码相位的测量。
本文为实现对GPS信号的精密跟踪,提出了一种兼备码相位和载波多普勒高精度测量的基带信号处理方法。将跟踪环路中解调后的伪码信号与接收机本地码发生器信号的相位差表征为TDOA,将混频信号与本振信号的多普勒频差表征为FDOA,再采用Hough变换结合一元线性回归的计算方法,分别解析这两路不同信号的时域和频域相位谱的条纹斜率,由此得到准确的TDOA和FDOA参量。该方法在低载噪比环境下跟踪精度有明显提升,即使在高动态变化时也能实现稳定跟踪。
2 相位条纹法的跟踪实现
2.1 TDOA相位条纹测量原理
TDOA测量原理是利用频域相位参数实现的。由维纳-辛钦定理可知,信号的相关函数与其功率谱密度函数互为傅里叶变换。因此,由相关函数在时域所表示的TDOA信息,可以由信号功率谱在频域的相移得到[16]。

GPS信号从卫星传输到接收机将产生一定的时延,本地码NCO生成的伪码会出现相位偏移,为实现伪码解调,在信号跟踪时通过准确测量码相位差,并对码NCO进行实时调整,达到复现出与接收信号相位一致的伪码。根据上述TDOA的测量原理,本文以TDOA相位条纹为参量实现码相位的跟踪。
首先对接收机混频解调后的基带数字中频信号进行TDOA相位条纹测量分析,可写作

通过检测TDOA频域相位谱上的条纹斜率,再除以2π即可得到码相位偏移量。因此基于TDOA相位的码跟踪环结构如图1所示。
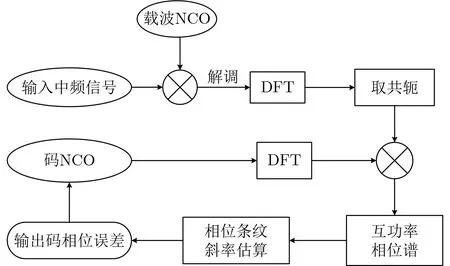
图1 基于TDOA相位条纹的码跟踪环结构
2.2 FDOA相位条纹测量原理
FDOA的测量原理是利用时域相位参数估计实现的。与TDOA的区别在于,它需要对两路频移信号分别做希尔伯特变换,再计算时域互相关功率谱,通过分析时域相位条纹的斜率,测量出信号的频偏。
由于卫星和接收机之前存在相对运动,为消除多普勒效应的影响,需要载波跟踪环准确测量载波多普勒频移,对载波NCO进行实时调整。因此根据上述FDOA的测量原理,本文以FDOA相位条纹为参量实现载波多普勒跟踪。
接收机载波跟踪环输入信号为载波多普勒频移调制下的中频信号,可写为

其中,v为卫星与接收机之间的相对速度,f0为中心频率,c为光速, Ts为采样间隔,θ为初始相位。
由于导航电文D是由±1的数据构成的,采用平方检波的方法可剥离导航电文,得到载波平方信号为

通过分析计算FDOA时域相位,将条纹斜率除以4π即可得到载波多普勒频偏,条纹截距除以2得到载波相位差。因此基于FDOA相位的载波跟踪环结构如图2所示。

图2 基于FDOA相位条纹的载波跟踪环结构
2.3 误差分析
根据上述测量原理计算BPSK信号的TDOA,得到的互相关功率幅度谱和相位谱,如图3所示。
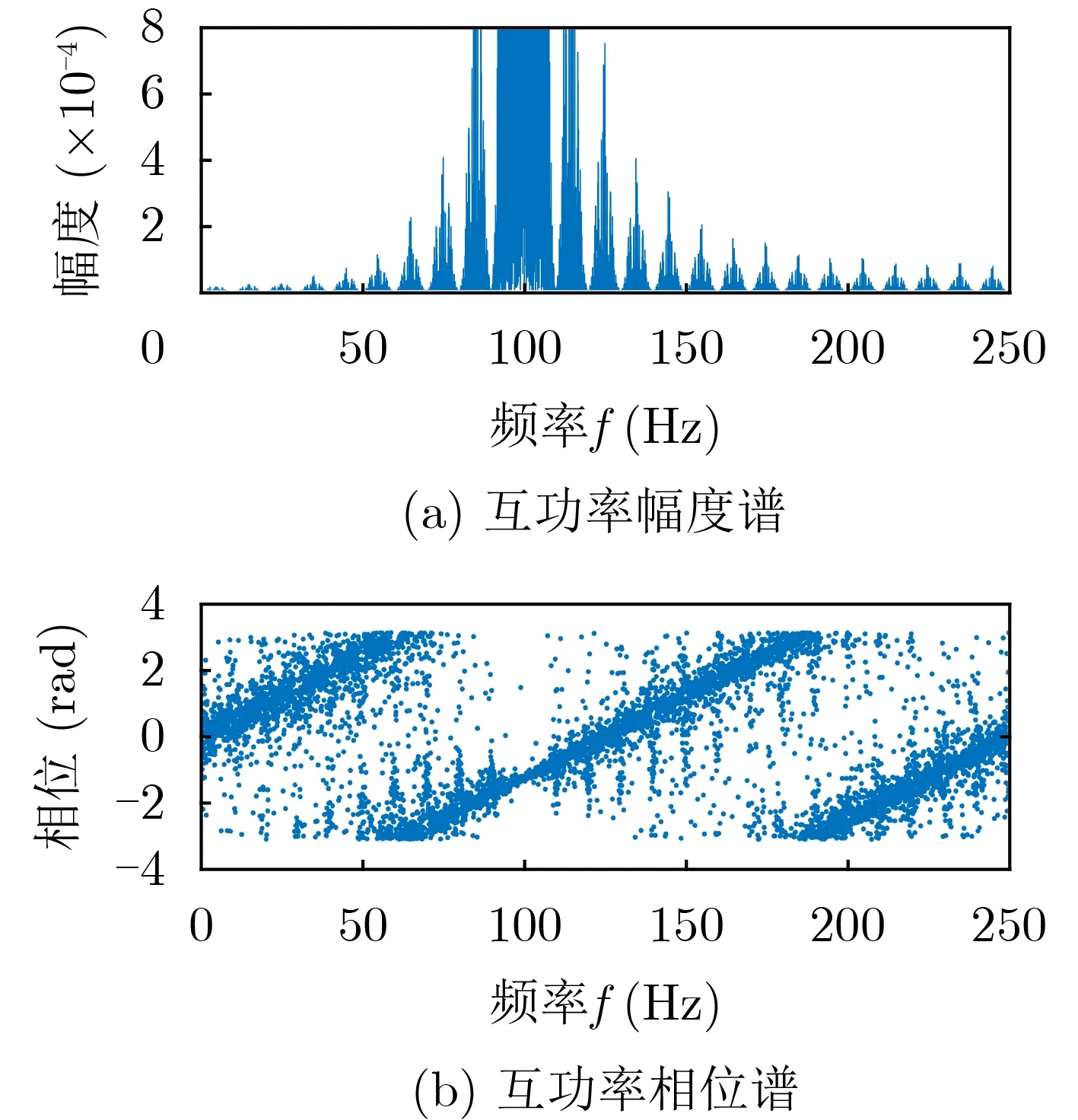
图3 BPSK信号的TDOA相位条纹
从相位谱中可以看出条纹分布并不是完全准确的直线,存在误差波动。考虑到计算机处理的信号是有限长的,当计算两路时延信号在[0,T]时间范围内的互功率谱时会引入计算误差,如图4所示。

图4 有限长信号的相关计算误差
图中xA(t)是由xB(t)延迟时间τ得到的信号,当对两个信号在t∈[0,T]上做相关运算时,可以看出zA与zB是两段多余的非相关信号;只有xA(t)在t∈[τ,T]时的信号,与xB(t)在t∈[0,T-τ]时的信号是完全相同的相关信号,故将其设为xAB。因此计算机得到的互相关功率谱结果为

由此得出结论1:TDOA/FDOA相位条纹测量算法,具有待测量越小计算结果越精确的特点。
除此之外,结合互功率幅度谱,还存在另一种计算噪声,噪声的大小与频率有关。在互功率谱幅度很小的频点处相位又明显发散,这是由于计算机的量化误差在做DFT时累积放大了。
由此得出结论2:相位谱数据的可靠性与对应频点的互功率幅度值呈正比。设置幅度阈值舍去对应幅度值较小处的相位,可提取更加清晰的相位条纹。
3 相位条纹斜率检测方法
将接收机产生的信号与接收的卫星导航信号之间的码相位差和载波多普勒频偏考虑为TDOA和FDOA,通过实时估算TDOA和FDOA的相位条纹斜率,可实现卫星导航信号跟踪。由于相位谱具有多条纹周期性排列的特点,随着TDOA和FDOA的改变,每条条纹的位置也在发生变化,因此采用一种自适应的方法识别出条纹中最清晰直线的位置,再对范围中单根条纹进行一元线性回归计算斜率,图5为相位条纹斜率的估算过程。

图5 相位条纹斜率估算过程
3.1 相位条纹的Hough变换
Hough变换是一种能有效识别多根直线的数据处理方法,其基本原理为将数据空间中以x, y为坐标轴的直线方程表达式,转变为以斜率a,截距b为坐标轴的直线方程表达式。在直角坐标系xOy中,一条直线的方程表达式为y =a*x +b*,在直线上任取一点(x0, y0),对于该点直线方程可写成b=-x0a+ y0,此时a, b为变量,定义aOb坐标系为Hough空间。若选取直线上若干点(xi, yi),即可在Hough空间中得到若干条直线方程b=-xi∙a+yi,那么所有直线都将交于点(a*, b*)。
如图6所示,数据空间中的一点,对应Hough空间中一条直线;数据空间中一条直线上的若干点,对应Hough空间中交于同一点的若干条直线,交点(a,b)就是数据空间直线的斜率和截距参数。

图6 Hough变换的直线参数估计

为避免数据空间中a趋于无穷大,将直线参数方程写成极坐标的形式其中,θ是数据空间中直线对应法线与x轴的夹角,直线斜率a=tan(θ+π/2),再根据三角函数的性质有

根据以上相位条纹Hough变换的原理,在计算机上的算法实现过程如下:

(2) 定义一个全零矩阵HN×M作为离散Hough空间的存储矩阵,矩阵的每个元素H(ρn,θm)对应离散Hough空间的一个格点。
(3) 将数据点(xi,yi)代入式(14),对方程ρ=xicosθ+yisinθ 遍历θ的M个离散取值,计算相应的ρ值,在Hough空间中寻找与其距离最近的离散点ρn,该点对应矩阵元素值H(ρn, θm)=H(ρn,θm)+1。
(4) 待相位谱中的所有数据按照步骤3执行完毕后,统计出矩阵H中的峰值H(ρ*,θ*)。
输出:确定峰值对应元素(ρ*,θ*),在相位条纹中找出以此为参数的直线

由此为接下来做直线拟合提供了相应的相位谱数据。
3.2 幅度谱加权的一元线性回归法
在Hough变换检测出条纹中有效数据范围后,需要对数据进行直线拟合。根据前面误差分析的结论,为提高相位谱数据的可靠性,采用一种基于幅度谱加权的一元线性回归算法。

4 仿真实验
首先利用MATLAB软件仿真生成GPS的L1频点基带信号,为了验证算法的静态跟踪精度,设置接收信号的中频载波频率为6.5 MHz,采样率为28 MHz,环路更新率为10 ms,经过粗捕获后进入跟踪环路的多普勒频差为200 Hz,码相位偏差10 ns。通过软件编程对相位条纹跟踪方法进行仿真实验,仿真结果如图7-图9所示。
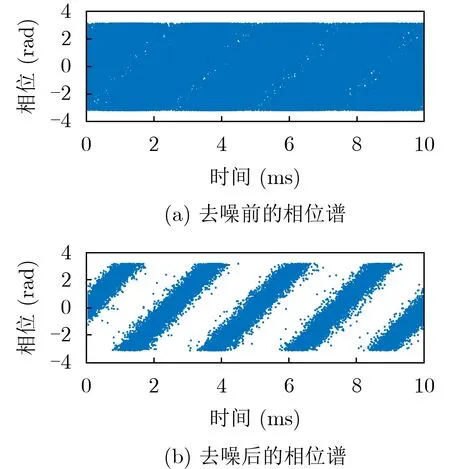
图7 GPS信号的时域相位谱
图7(a)为接收信号与本地载波信号的时域相位谱,可以看出条纹淹没在噪声中,图7(b)为依据幅度阈值去噪后的相位谱,相位条纹明显清晰了。图8为时域相位谱在分辨率为120×120 dpi的Hough空间下的数据表征,沿ρ轴看有5个峰值,表示了相位谱中有5条直线,沿θ轴可以看出ρ的5个峰值基本对应同一个θ,这表示相位条纹的5条直线都具有相似的斜率。再根据θ和ρ的最大值从相位条纹中提取出最可靠的一段数据,然后对这部分相位点做幅度谱加权的一元线性回归,如图9所示,回归直线的斜率除以4π即为载波多普勒的鉴频结果。
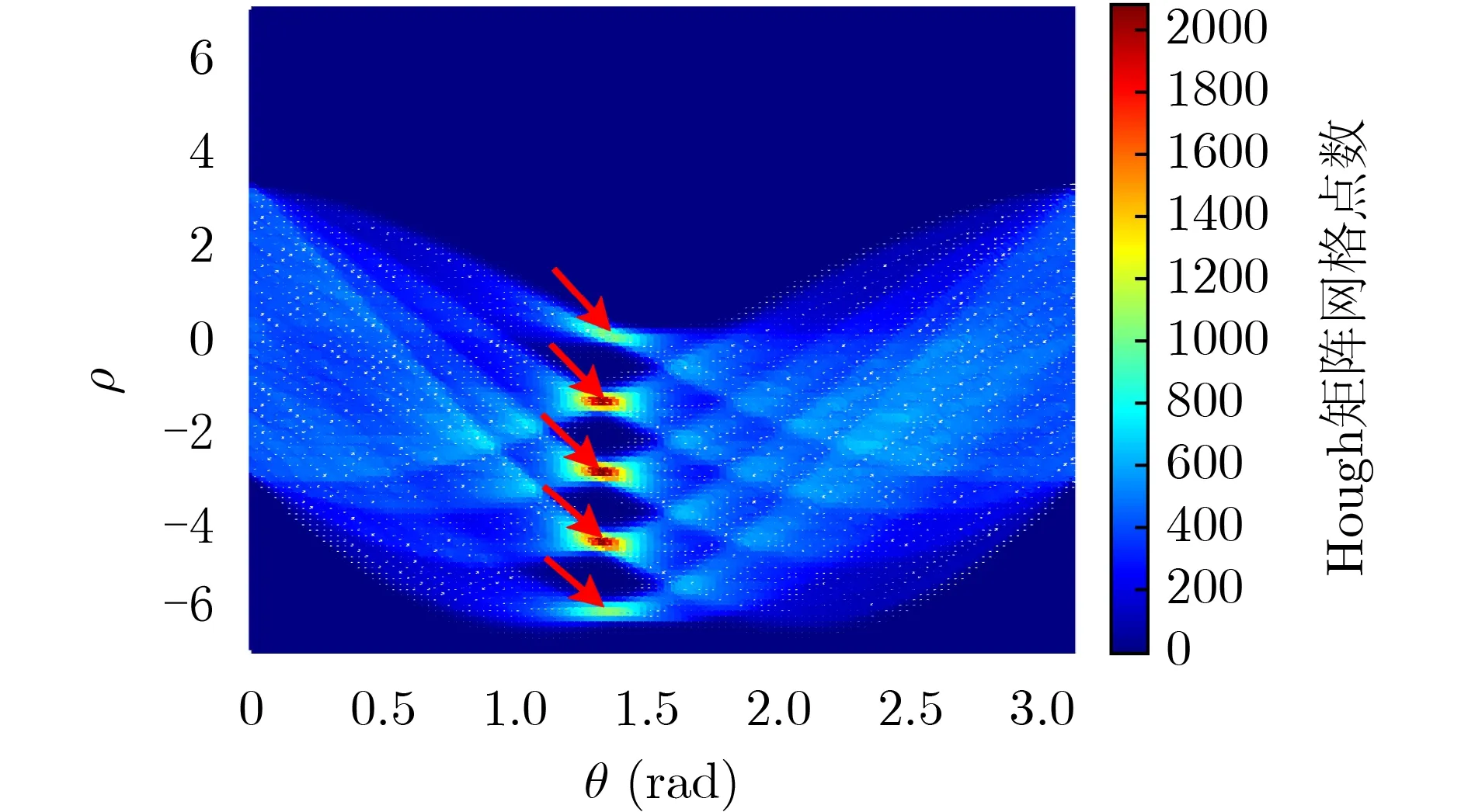
图8 相位条纹的Hough变换

图9 幅度加权的线性回归结果
然后在不同载噪比情况下分别进行1000次蒙特卡罗仿真,载波跟踪误差与环路带宽为30 Hz的2阶锁频环进行对比,其热噪声误差为[17]

仿真结果的鉴频误差均方差(RMSE)如图10所示,相位条纹算法在低载噪比时鉴频精度具有明显优势。当载噪比为32 dB-Hz时,载波多普勒频偏的跟踪误差均方差为13.42 Hz,相对2阶锁频环精度提高了约31%。随着载噪比的提高,相位条纹算法的鉴频精度与锁频环逐步接近。码相位跟踪误差与延迟锁定环进行对比,仿真结果的测量误差均方差如图11所示,相位条纹算法的鉴相精度也明显优于延迟锁定环。当载噪比为32 dB-Hz时,码相位测量误差均方差为2.92 m,相对延迟锁定环精度提高了约60%。

图10 载波多普勒测量误差均方差对比
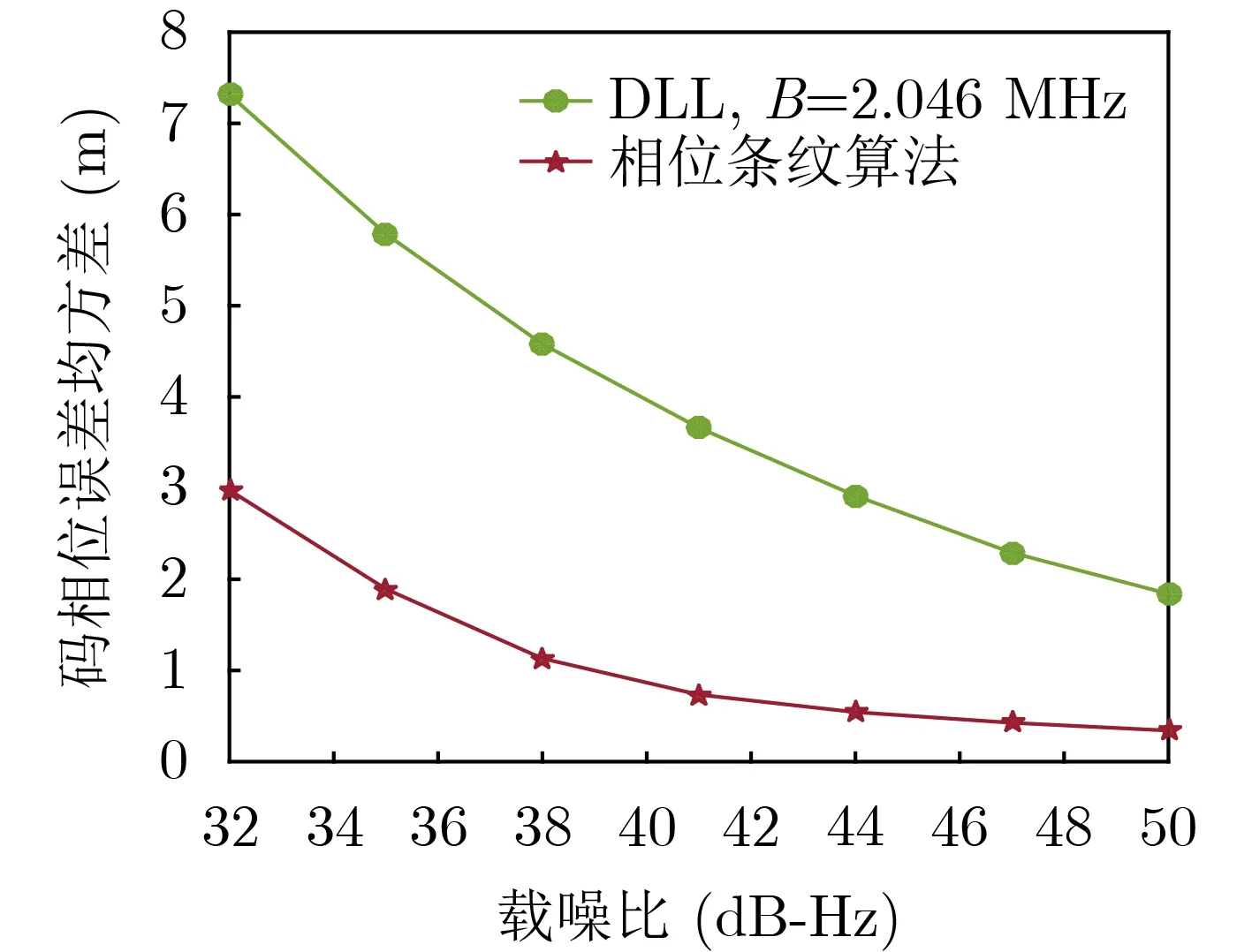
图11 码相位测量误差均方差对比
为了验证相位条纹算法的动态适应性,根据美国喷气推进实验室(JPL)的高动态模型,设置接收机与卫星的相对运动状态。初始速度为100 m/s,0~0.5 s有-25 g(1 g≈9.8 m/s2,下同)的恒定加速度,然后在0.5~1 s引入100 g/s的加加速度,输入信号载噪比设置为44 dB-Hz。此时高动态模型的载波跟踪结果如图12所示,可以看出相位条纹法能精确跟踪载波多普勒,其跟踪误差如图13所示,对比环路带宽为60 Hz的传统PLL-FLL算法,相位条纹算法的鉴频误差更小,尤其是在0.5~1 s即使有较大的加加速度它的误差也不会有明显增大。且相位条纹法的频率跟踪误差在0~0.4 s逐渐减小,0.4~0.7 s又逐渐增大,可以看出相位条纹法的鉴频误差与多普勒偏移量呈正比关系。高动态模型的码相位跟踪误差如图14所示,其中相位条纹算法相较DLL算法有明显优势,表现出和多普勒测量相同的特性。

图12 高动态信号的载波跟踪结果
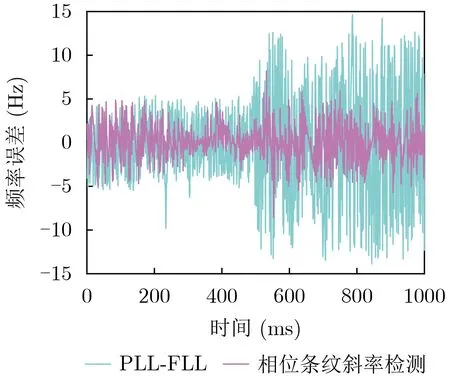
图13 高动态信号载波跟踪误差对比

图14 高动态信号码相位跟踪误差对比
5 结束语
本文提出了一种基于TDOA和FDOA相位条纹检测的GPS信号跟踪方法,并采用该算法对GPS接收机在不同运动状态下的信号跟踪进行了分析,结果表明:
(1) 算法的跟踪精度高,在32 dB-Hz的低载噪比环境下,对静态信号的码相位跟踪误差均方差为2.92 m,相对延迟锁定环精度提高了约60%;载波多普勒频偏的跟踪误差均方差为13.42 Hz,相对2阶锁频环精度提高了约31%。
(2) 算法的动态适应性优良,在载噪比为44 dB-Hz的环境下,可实现对JPL高动态模型(初始速度100 m/s,加速度25 g(1 g≈9.8 m/s2,下同),加加速度为100 g/s)的载波跟踪。且应对加加速度时,跟踪精度对比传统PLL-FLL方法具有明显优势,误差均方差减小了约50%。
(3) 算法具备同时测量码相位和载波多普勒的能力,将码跟踪环和载波跟踪环高度耦合起来,可简化接收机跟踪环路的设计。
综上所述,在高动态或低载噪比环境下,基于TDOA和FDOA的频域和时域相位条纹的GPS信号跟踪方法相比传统的码跟踪环和载波跟踪环都更占优势。同时该方法能够兼并码跟踪环和载波跟踪环,构造出一种较低成本的跟踪结构,具有重要的GPS接收机应用价值。
