双正交小波对球面渐开线螺旋锥齿轮齿面拟合的研究

2022-09-22王永旭阿达依谢尔亚孜旦刘明亮

机床与液压 2022年2期

王永旭，阿达依·谢尔亚孜旦，刘明亮

(新疆大学机械工程学院，新疆乌鲁木齐 830047)

0 前言

螺旋锥齿轮是机械传动系统中最重要的核心部件之一，用于传递空间中两相交或交错轴之间的动力，具有重合度大、传动平稳、噪声小、承载能力高、传动效率高等优势，广泛应用于汽车、航天航海、矿山机械等领域[1]。随着工程应用领域的扩展，对螺旋锥齿轮的加工精度提出了更高的要求。齿面精度直接影响传递运动的准确性、平稳性和载荷分布的均匀性，齿轮的精度越高，传递的运动精度越高，机械效率越高，承载能力越强，耐磨性越好，疲劳寿命越长，机械振动和噪声越小[2]。传统的加工方法加工复杂曲面时，既不能达到预期目的，也无法满足现代加工高精度、高柔性、高效率的要求。因此，多轴通用数控机床加工螺旋锥齿轮被提出，并成为重要的研究方向和热点。唐进元等[3-4]采用反调修正法提高了螺旋锥齿轮的加工精度。韩江等人[5]利用刀盘误差的补偿提高螺旋锥齿轮齿面加工精度。农小锐[6]提出采用先进的数控加工技术与合理的后处理是提升螺旋锥齿轮加工精度的主要途径。阿达依·谢尔亚孜旦等[7]利用电化学光整加工改变齿面几何微观形貌，从而提高了加工精度。以上方法和途径虽然提高了加工精度，但都是集中在加工过程和成形后处理，并没有建立加工前的数字化模型。由文献[8]可知用于加工的数字化模型的表面光顺性和复杂程度是最终影响加工质量的决定性因素。

根据小波理论，曲面可以分解为表示主体特征的低频曲面与表示细节特征的高频曲面，而高频细节特征曲面是影响曲面光顺性和复杂性的主要因素。因此，本文作者运用NURBS曲线曲面及其插补算法[9]在高精度数控加工中的优势，结合双正交B样条小波分解与重构，以减小高频曲面对曲面光顺性的影响，在保证设计精度的前提下，降低齿面的复杂性和提高齿面的光顺性,为利用通用多轴数控机床加工球面渐开线螺旋锥齿轮提供参考。

1 理论基础

1.1 球面渐开线理论与方程

球面渐开线是当平面在圆锥面上作纯滚动时，平面上一点的运动轨迹，该圆锥称为基圆锥。如图1所示，圆平面π与基圆锥面OAO′相切并在锥面上作纯滚动，圆平面π上的一动点K在空间的运动轨迹就是一条渐开线。由于动点K在渐开线上任意一点位置到基圆锥顶点O的距离始终相等，该渐开线是以点O为球心的球面上[10]。圆平面由初始位置OK滚动到位置OA，动点K的运动轨迹称为球面渐开线AK。

图1 球面渐开线理论

在直角坐标系中，利用空间球面几何学建立球面渐开线方程。在动直角坐标系OX1Y1Z1中，OK的方程为

(1)

其中：r为OK的长度；δ为基圆锥的根锥角。根据坐标变换原理，得到动坐标系OX1Y1Z1坐标方程：

(2)

把公式(1)代入公式(2)得到球面渐开线方程：

(3)

改变r和γ的值，可以得到齿面上不同位置点的坐标[11]。锥齿轮的齿形是由基圆锥上的起始点的集合所决定的:如果基圆锥面上的起始点的集合是一条直线，该齿轮是直齿锥齿轮;如果是一条斜线就是斜齿锥齿轮;如果是一条螺旋线就是螺旋锥齿轮。

1.2 引入螺旋线

由螺旋角的广义定义[12]可知，任一螺旋线都可以看作空间的点绕中心轴作回转运动所产生的运动轨迹。在运动轨迹上任意一动点的速度可以分解为3个方向上的速度分量，即轴向速度矢量(速矢)v1、径向速矢v2、切向速矢v3，如图2所示。

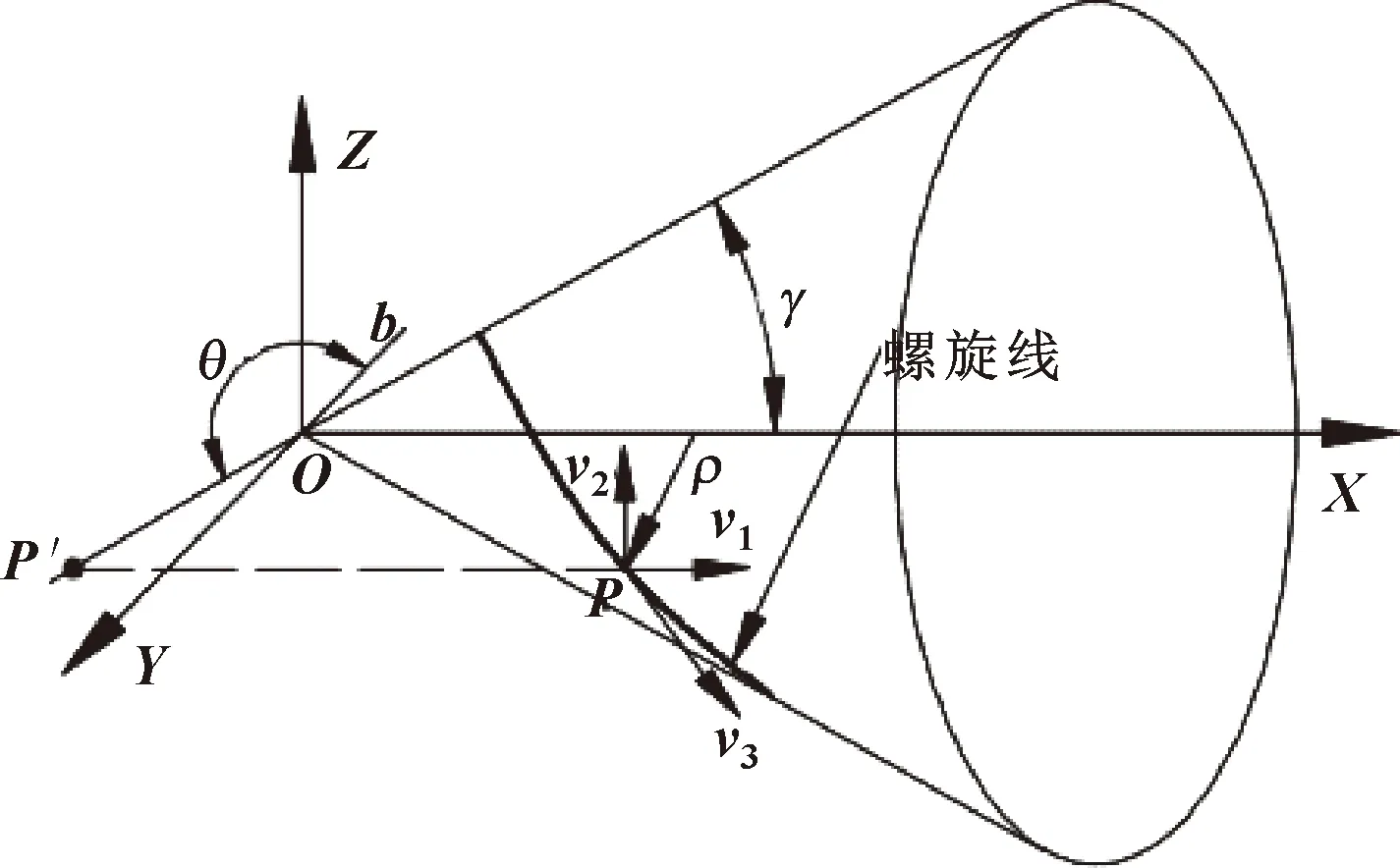
图2 螺旋线的形成过程

运动点P沿着X轴向右运动的同时作回转运动，所以点P处螺旋角广义定义为

(4)

以回转体圆锥面为例，对于每一个x值，ρ是定值。在极坐标中，ρ=ρ(x)，则可以得到3个方向的速度大小：

(5)

将式(5)代入式(4)可得：

(6)

设圆锥的半顶角为γ：

(7)

将式(7)代入式(6)可得：

(8)

所以在圆锥面上的螺旋线方程为

(9)

1.3 算例

以一副无变位的标准球面渐开线螺旋锥齿轮为例，主要参数见表1。运用MATLAB编写离散点程序，得到齿面上6×11个离散点坐标值，以大轮的凹面和凸面为例，离散点和网格如图3所示。

表1 一副啮合的螺旋锥齿轮主要参数

图3 大轮齿面离散点和网格

2 齿面的NURBS曲面拟合与小波变换

2.1 三次NURBS曲面的表达式

三次NURBS曲面的方程为

u,v∈[0,1]

(10)

式中:Pi,j是控制顶点坐标;ωi.j是权因子;Ni,3(u)、Nj,3(v)分别是u、v方向上的三次B样条基函数,可由DeBoor-cox递推公式确定。DeBoor-cox递推公式为

式中:k是方程的次数。利用NURBS插值法可以反算出权因子和控制顶点的值,反算参考文献[13]159。节点矢量u、v采用累积弦长法确定。

2.2 NURBS曲面的三次B样条小波分解与重构

小波变换本质是把信号分解成低频主体特征信息和高频细节信息，重构是对分解的逆过程。小波变换可分为离散(DWT)和连续(CWT)小波变换。若函数f(x)∈L2(R)，则CWT小波的表达式为

(11)

在实际工程中得到的大部分是离散信号,要求运算量小和运算能力强，同时还必须有较高的准确度。DWT小波表达式为

(12)

其中:T是f(x)的维度;t为离散时间抽样指数。

小波变换原理的实质是对控制坐标点的分解与重构，则对NURBS曲面进行双正交B样条小波基变换是把NURBS曲面分解为低频主体曲面(光顺性好)和高频细节曲面(光顺性差)。

(13)

(14)

S(u,v)=

(15)

(16)

由于是保留低频主体特征信息，则去除高频细节信息，令P1=0、P2=0、P3=0，从而可以得到反算坐标控制点Pi,j，把Pi,j代入NURBS曲面的方程可以去除高频细节信息的曲面，从而达到降低齿面的复杂性和提高曲面光顺性的目的。将生成的NURBS网格曲面导入到UG12.0进行建模，齿轮的装配模型见图4。在被小波处理的NURBS曲面上取50个数据点进行拟合误差计算，结果如图5所示。

图5 拟合误差

原始齿面与小波处理后的齿面的高斯曲率如表2所示。可以看出：小波处理后的齿面高斯曲率变小，同时曲面的复杂程度也随之降低并且光顺性提高。复杂曲面的复杂程度的降低，有利于减小铣削加工过程中最大残余力，从而提高加工效率和加工精度[8]。小波处理后的复杂曲面的复杂程度降低，所以对球面渐开线螺旋锥齿轮的齿面运用小波优化可以在很大程度上提高螺旋锥齿轮齿面的加工精度。

表2 齿面的高斯曲率

在加工过程中，应尽可能地减小加工误差和保证加工精度，所以可以从以下2个方面进行优化：

(1)对刀具的运动轨迹和走刀步长进行优化。在数控加工过程中，刀具运动轨迹的优化可以改善加工质量和提高材料的去除效率。走刀步长是刀具轨迹上相邻2个插补点之间的距离。由几何关系可知走刀的步长公式为

(17)

式中：Rmin为最小曲率半径；δ为误差。

其中：A=yC-yB；B=xB-xC；C=yBxC-xByC。文献[15]中证明了合理的步长可以弱化因插补方法而造成的误差。

(2)对进给速度进行优化。在加工过程中要确保加工精度，应避免造成较大的轮廓误差，插补时进给速度应该满足式(18)。在加工中，为防止加速度过大而对机床造成冲击，加速度应满足式(19)：

(18)

(19)

式中:ρi是曲率半径；δmax为最大轮廓误差；Ts为插补周期；vi为第i个插补周期的进给速度；amax为系统的许用最大加速度[9]。

3 实验验证

3.1 实验条件

以大轮为例进行实验验证，运用UG12.0构建球面渐开线螺旋锥齿轮的单齿模型,如图6所示。运用UG中特殊模块，进行数字模拟加工并导出数控加工代码，把加工代码导入到数控铣床中进行数字化加工。毛坯的材料为45号钢，尺寸为60 mm×50 mm×30 mm。加工需要运用的设备及加工参数见表3，加工过程如图7所示。

图6 数字化模型

表3 加工参数

图7 数控加工过程

对数控加工后的工件，用三坐标测量仪(TASASTAR-m)对螺旋锥齿轮的齿面(凹面和凸面)进行测量，如图8所示。首先将工件固定在三坐标测量仪的测量台面上，以工件底面的中心作为三坐标测量仪的原点并建立坐标系，均匀分布测量齿面的凹面和凸面上离散点坐标数据。

图8 测量装置

3.2 实验结果与分析

将三坐标测量仪测量的数据点与理论数据点进行比较，可以计算出齿面加工误差。小波优化后加工的球面渐开线螺旋锥齿轮齿面上凸面和凹面的加工误差分布如图9所示。图10所示为齿面加工误差。

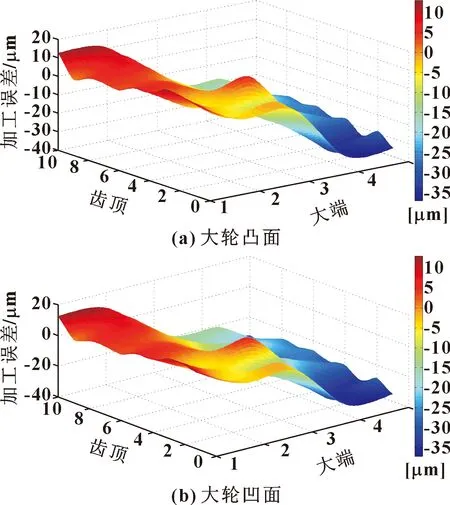
图9 小波优化加工误差分布

图10 齿面加工误差

由图9可以看出:齿面(凸面和凹面)的加工误差呈现出相同的趋势，齿根加工误差比较大,这是因为球面渐开线螺旋锥齿轮的齿根结构比较复杂，在实际加工过程中机床的振动和测量误差等因素都会对实验结果产生影响。

由图10可知:通过小波处理的齿面拟合误差近似为加工误差的1/3，而未经小波处理的齿面拟合误差近似为加工误差的1/6。经过小波处理后的齿面拟合误差比未处理的齿面大，但是较小的加工误差彰显了小波变换在齿面优化上的优势。

由表2可知:经过小波处理后的齿面的高斯曲率减小，并且原始凹面和凸面与小波处理的凹面和凸面的高斯曲率极差分别减小了1×10-3、1.01×10-3，说明降低了齿面的复杂性，提高了齿面的光顺性。由图10还可以得到经小波变换后的球面渐开线螺旋锥齿轮的齿面的凹面和凸面的平均加工误差分别减少了14.58、14.62 μm,说明齿面的复杂性越低，加工偏差越小，加工精度就越高。