基于SFS-SVM的V形件弯曲工艺参数优化研究
2022-09-22徐承亮曹志勇王大军胡吉全
徐承亮,曹志勇,王大军,胡吉全
(1.广州科技贸易职业学院产业学院,广东广州 511442;2.湖北大学材料科学与工程学院,湖北武汉 430062;3.重庆邮电大学自动化学院,重庆 400065;4.武汉理工大学物流工程学院,湖北武汉 430072)
0 前言
V形弯曲件是航空、航天、汽车工业中的一类常见零件。影响V形工件弯曲回弹的因素众多,工件尺寸、力学性能和负载条件等都使得V形件的弯曲回弹难以得到有效控制[1-2]。实际工程应用中往往采用反复试错法、有限元法[2]以及经验公式法解决这种高度复杂的非线性控制问题,但是反复试错法、有限元法非常耗时,经验公式法误差又较大。
支持向量机使用一个线性函数将原始空间映射到高维数据空间[3],但是计算较为复杂,要耗费大量的CPU时间去训练模型、提高其精度。研究表明,变量筛选算法可以产生精确的训练数据集和有效降低计算时间成本。现有的算法多是基于差分映射或梯度算法,这种算法只有在输入输出函数和目标值之间的差异较小时才能获得较好的预期效果,而实际中这种差异往往较大,从而导致模型预测精度较低。
顺序向前筛选(Sequential Forward Select,SFS)是一种精确性高、全局搜索并筛选特征变量子集的非线性降维算法。SFS法在搜素新的数据节点时都会调用支持向量回归(Support Vector Regression,SVR)进行收敛性判断,SVR 是基于回归问题的支持向量机(Support Vector Machines,SVM),其核函数参数寻优过程多采用耗时的交叉验证方法[4-5]。SFS算法部署在SVR模型框架内,搜索新的数据节点时,会快速完成特征变量子集的筛选和降维,大幅减少生成精确的SVR训练数据集的样本数据规模和计算时间成本,提升弯曲回弹元模型的生成效率,并仍能保证模型的收敛精度[5-7]。
1 实验模具与设备
V形工件在实际工程中应用非常广泛,在研究中采用的折弯模具和设备如图1(a)和(b)所示。模具主要由上、下模头组成。

图1 试验用弯曲模具和设备
一种典型V形零件弯曲模型如图2所示,在图2(a)所示的加载过程中,上模压下板料到成形终点状态,t是板料厚度,c是上模和下模之间的间隙,r是上模圆角半径(V形板料的圆角半径),θ是上模的张开角(V形板料的张开角)。由于弹性变形的存在,板料在卸载后会不可避免地发生弹性回复,也就是回弹,图2(b)显示了板料的卸载过程。对比图2(a)和(b)可以看到:卸载后板料发生了回弹,形状改变,其中V形板料的圆角半径由图2(a)中的r变成了图2(b)中的R,V形板料的张开角由图2(a)中的θ变成了图2(b)中的α,回弹大小由张开角的增量α-θ决定。板料回弹后的张开角α和圆角半径R与材料性能、上模压下量、上模下压速度、板料厚度等因素均有关系,而且之间的非线性关系复杂,内置规律的解析模型难以确定。
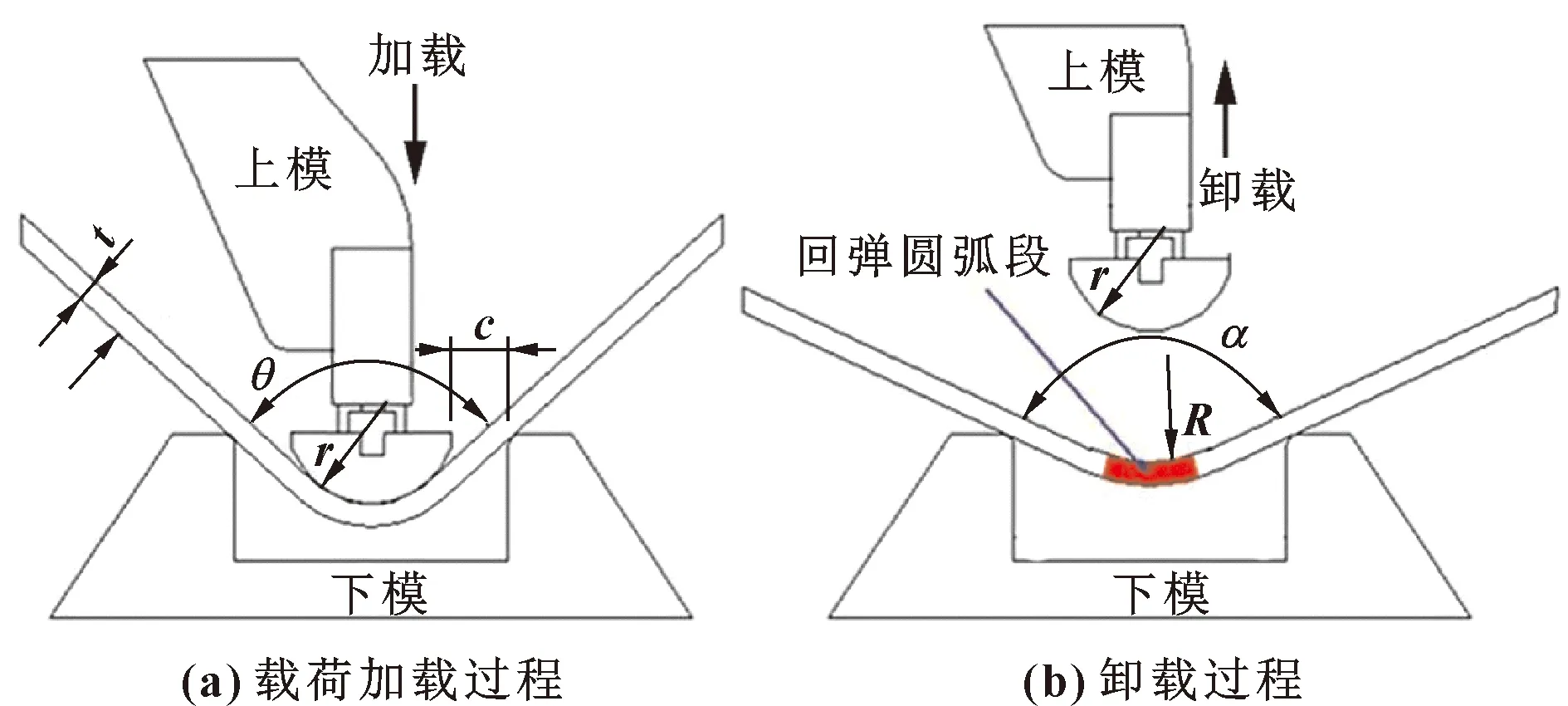
图2 一种典型V形零件弯曲模型
三维扫描测量仪用于扫描弯曲成形后的零件并获得三维的点云数据,然后将获得的数据导入计算机辅助设计软件中完成建模,最后将模型导入有限元分析软件获取弯曲成形零件的张开角α、板料圆角半径R。通过改变输入参数,重复前述过程,即可获得训练和测试用的数据样本集。
2 SFS-SVM算法
考虑以下弯曲回弹工艺参数对板料回弹后的张开角α和圆角半径R的影响:板料长度L,板料宽度B,板料厚度t,上模圆角半径(V形板料的圆角半径r),材料的力学参数σs/E,模具单边间隙c,上模行进速度v。基于以上弯曲回弹工艺参数构建支持向量机模型,并部署到顺序向前筛选算法中以高效筛选出最优的影响弯曲回弹工艺参数的特征变量参数子集,从而提高弯曲回弹模型预测结果的精度与可靠性。SFS-SVM模型算法如下:开始于空集,顺序增加特征X+使得当结合已筛选的特征Yk时能使得目标函数J(YK+X+)最优。具体描述如图3所示,主要由SVR模块和SFS变量筛选模块构成。
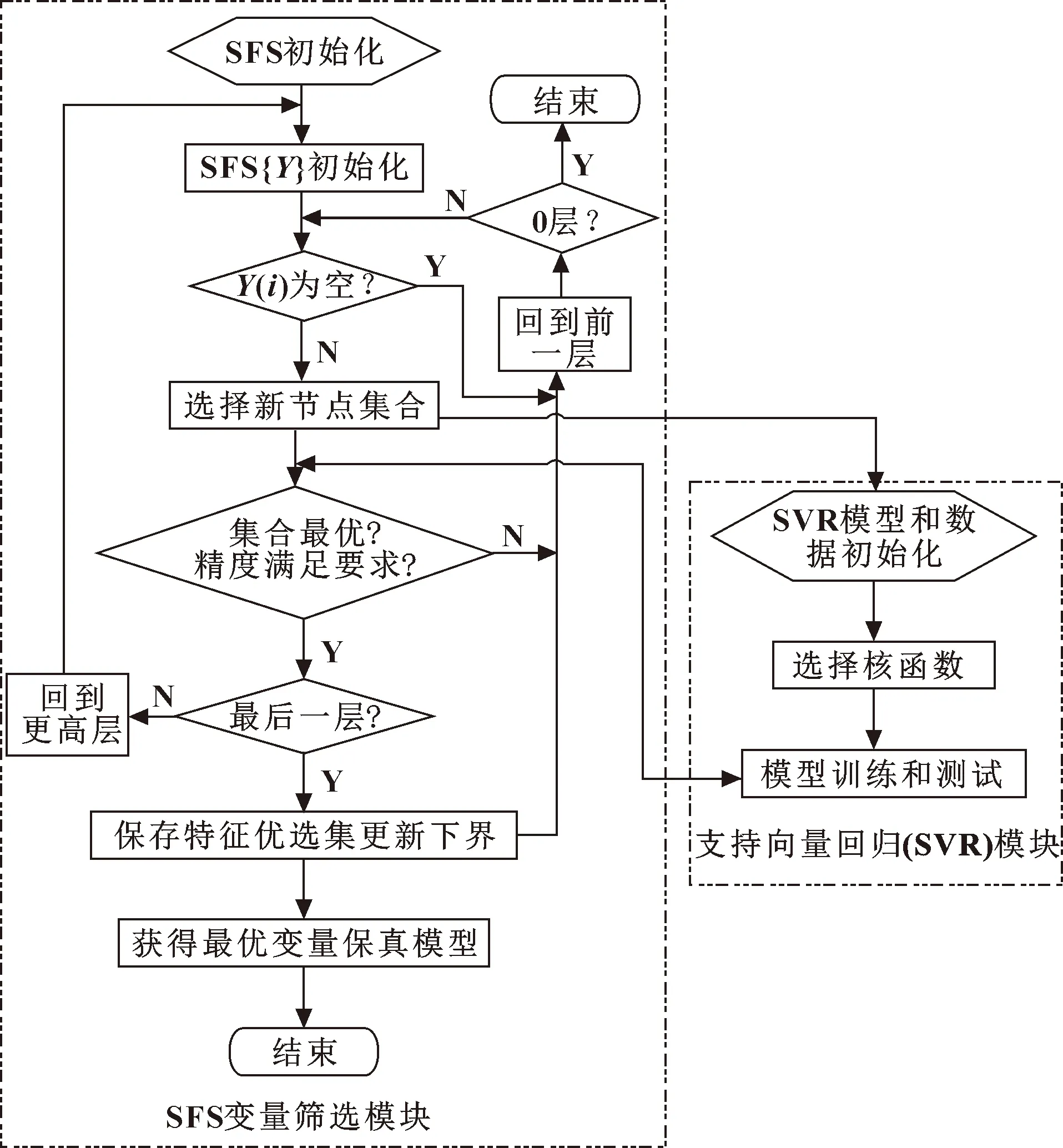
图3 基于SFS-SVM(SVR)的V形弯曲回弹算法流程
(1)开始于空集Y0={φ};
(3)采用基于递归核函数矩阵的 SVR 方法,避免耗时交叉验证与寻优的过程;
(4)更新YK+1=Yk+X+,K=K+1;
(5)返回步骤(2);
(6)对SVR 进行核参数寻优,最后对模型进行训练和测试。
3 有限元模拟
基于ABAQUS/Explicit模块求解塑性成形中非线性动力学问题,有限元模型包括上模(凸模)、板料和下模(凹模),如图4(a)所示。由于板料(工件)的长度和宽度远大于厚度,因此其塑性变形可以看着是一个平面应变过程。模拟成形过程中,将上模和下模看作刚性体,板料为拉格朗日弹塑性变形体,板料材料为表面硬化合金结构钢20MoCr4,弹性模量212 GPa,泊松比为0.3,采用厚壳小应变单元S4R,网格类型为八节点六面体线性减缩积分单元。板料尺寸取值范围:厚度t在2~5 mm内取值,长度L在80~100 mm内取值,宽度B在40~80 mm内取值,弯曲成形后V形板料的张开角α在42°~46°内变化,V形板料圆角半径R在8~12 mm内变化。板料有限元模型如图4(a)和(b)所示。
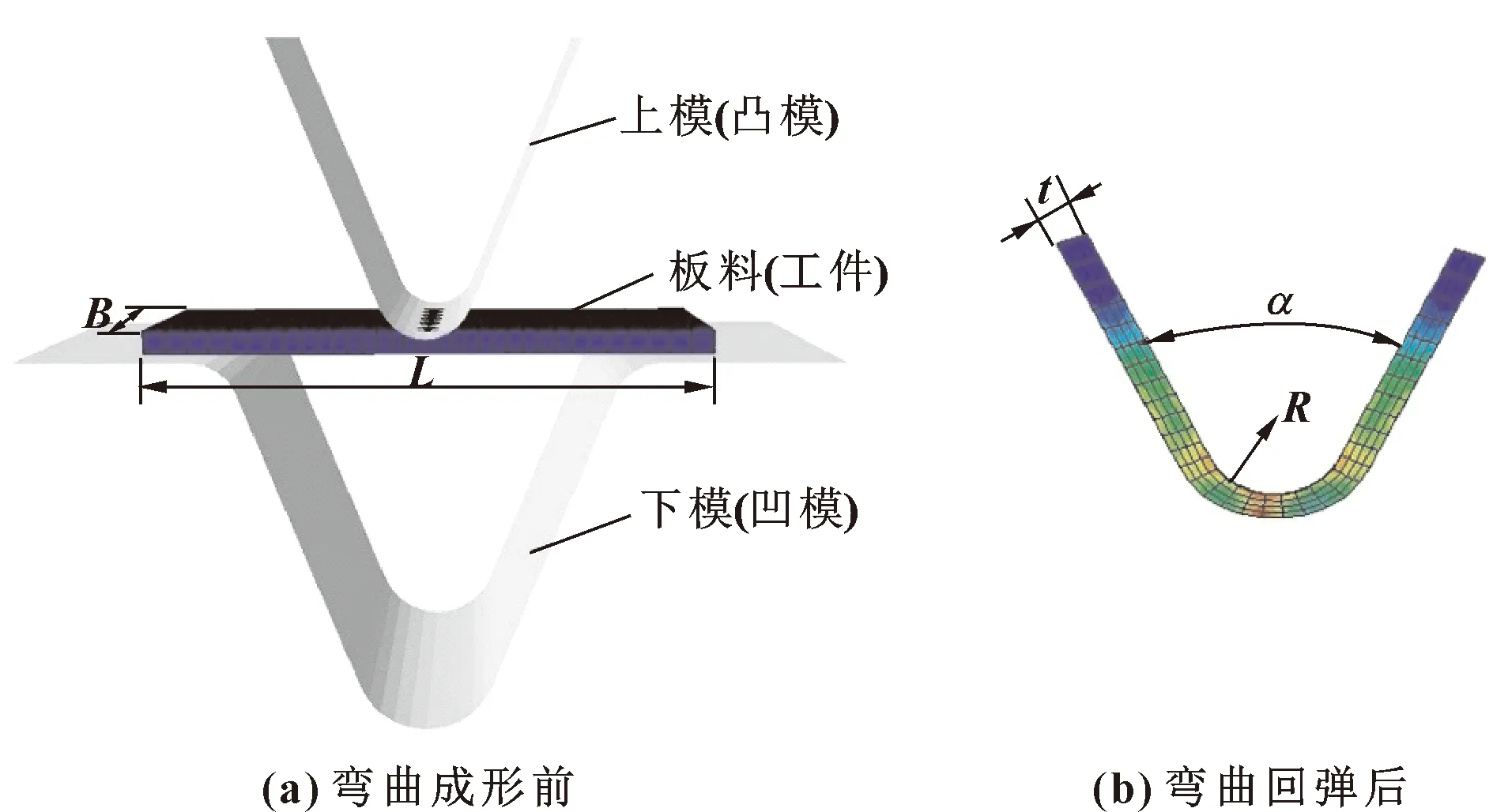
图4 实验研究用的有限元模型
4 结果与讨论
4.1 SFS-SVM算法优化结果
通过改变板料长度L和板料宽度B等7个输入参数的值,将模型导入有限元分析软件后可以求解获得弯曲成形零件回弹后的张开角α、板料圆角半径R,即可获得SFS-SVM算法训练和测试用数据样本集。实验中样本集共有95行,如表1所示。表2给出了板料长度L和板料宽度B等7个输入变量对SFS-SVR模型的目标α和R的预测结果的变量相关度排序情况,可以看出:7个输入变量中对输出结果α和R的相关度排序位于前4的分别是板料厚度t、模具单边间隙c、上模圆角半径r和上模行进速度v。
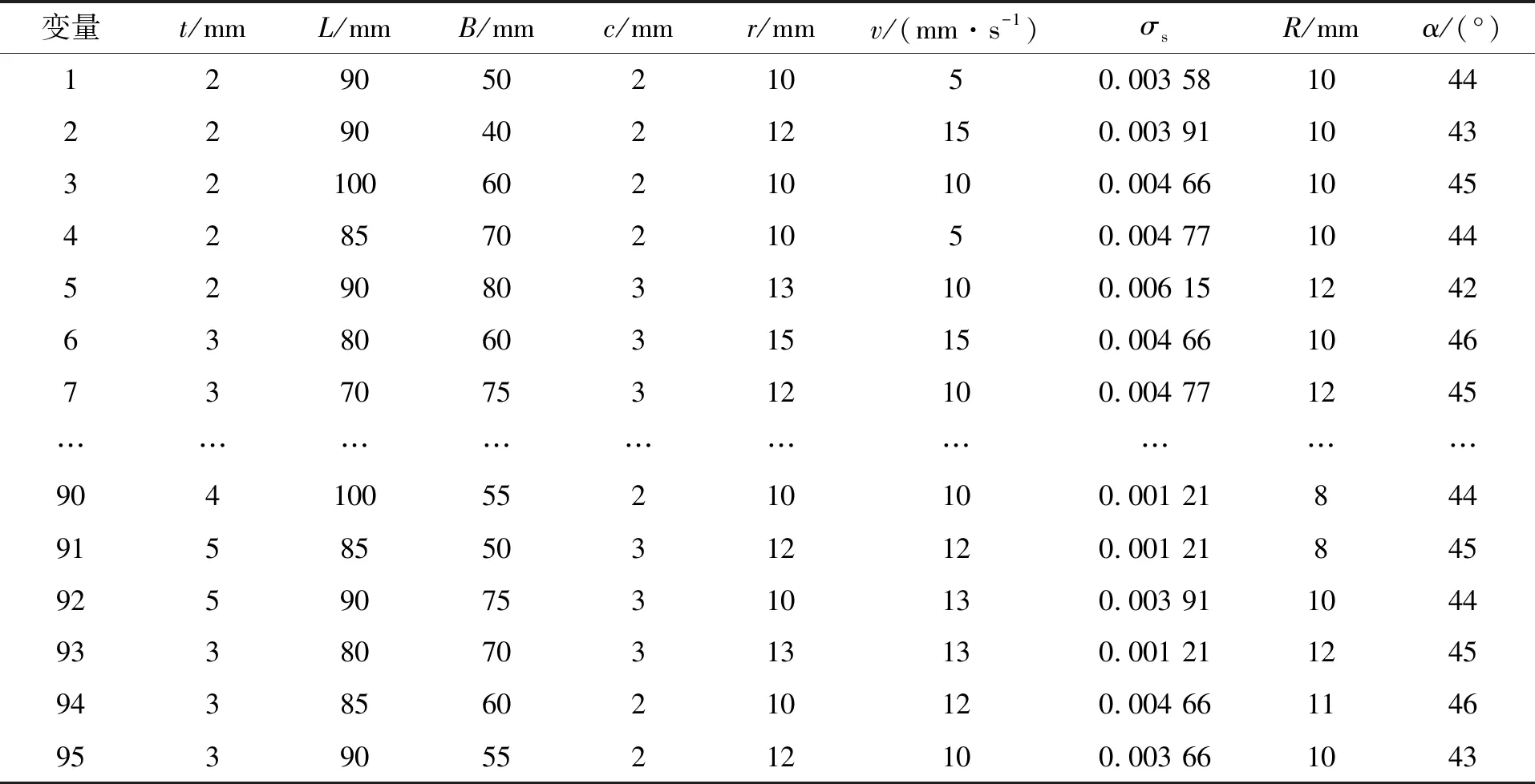
表1 SFS-SVM算法训练和测试用数据样本集
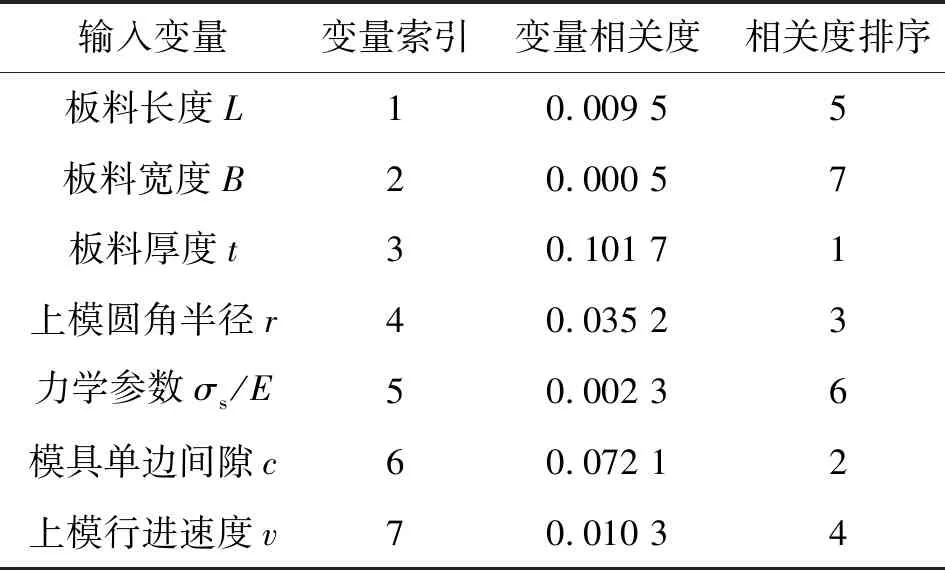
表2 输入变量的相关度排序结果
表3所示是一个由SFS-SVM 模型降维分析获得的最优变量集{t,c,r,v}的详细数据,可以看到:当维数为4时,特征变量子集由{t,c,r,v}组成时,算法拥有较高的模型决定系数(R2=0.972 213)和较低的均方误差(MSE为0.004 11),算法模型的预测精度相对较高。

表3 特征变量筛选示例(测试集)
4.2 有限元模拟结果
对V形弯曲回弹进行有限元数值分析,并对回弹试验结果进行验证。有限元分析分3个步骤进行,即加载步、保持步和卸载步。图5给出加载和保持步中上模压下到和坯料完全接触状态下坯料的Mises应力分布云图,可以清晰地看到:与加载步骤相比,圆角部分Mises应力在卸载步发生了少许增大趋势,这主要是弯曲回弹效应导致的结果。从图5还可以看到:塑性变形区主要集中在圆角处,其他区域,尤其是板料上端变形较小,甚至可以看做是刚性平移区。图6给出上模移开卸载后板料发生回弹后的示意图,板料内部在发生塑性变形时,由于弹性变形的存在,导致卸载后板料发生弹性回复。回弹后的张开角α、板料圆角半径R如图6所示。

图5 上模压下到和坯料完全接触状态下坯料的应力分布云图
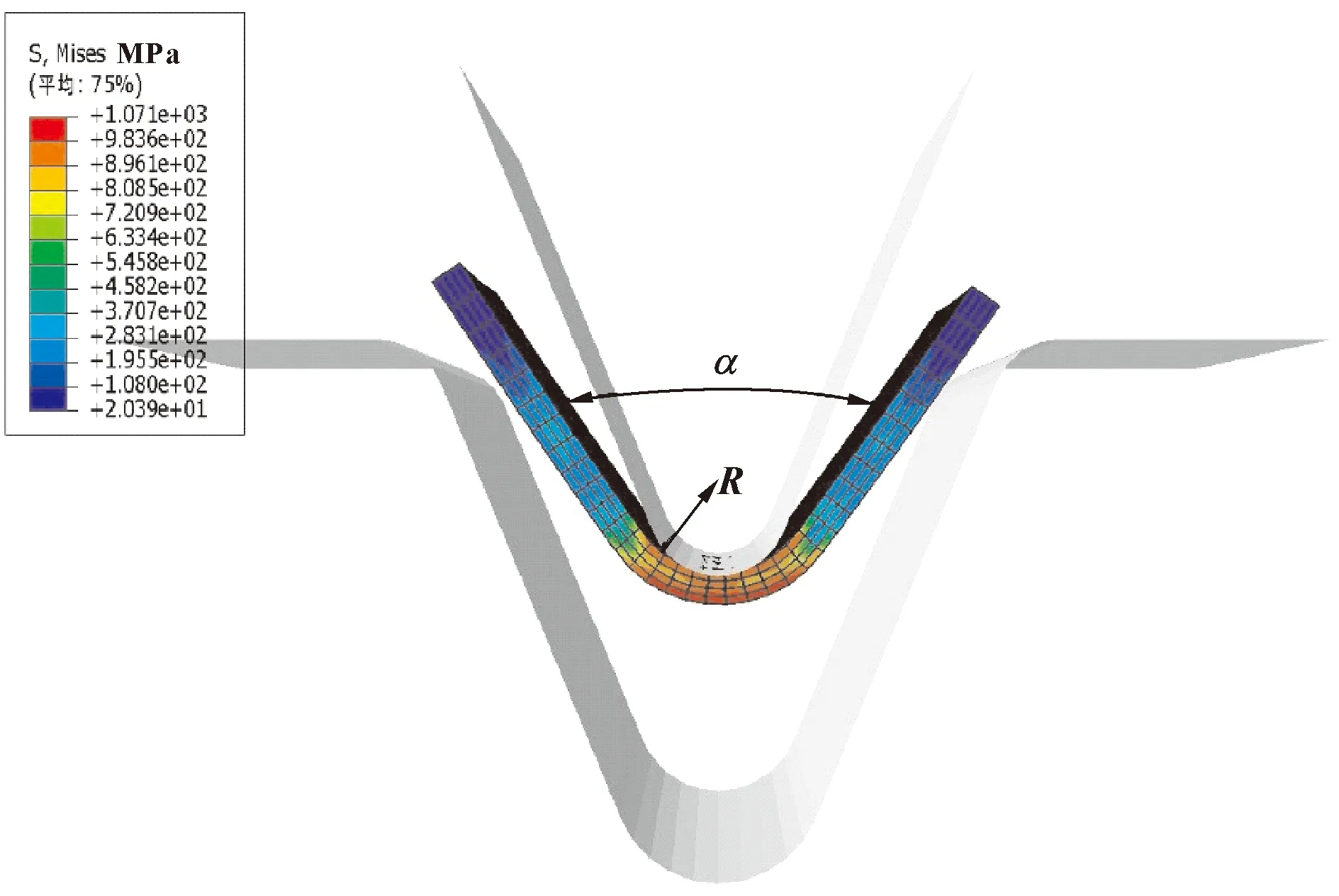
图6 上模移开卸载后板料发生回弹后的示意
4.3 实验对比
在板料长度L取80 mm、板料宽度B取60 mm、板料厚度t取3 mm、上模圆角半径r取10 mm、材料的力学参数σs/E取0.004 12、模具单边间隙c取10 mm、上模行进速度v取10 mm/s,基于图1中的实验模具和设备进行V形件弯曲实验,实测得的成形零件回弹后的张开角α、板料圆角半径R分别为44.6°和11.5 mm,如图7所示。Abaqus有限元方法、SFS-SVM算法和弯曲实验获得的弯曲成形零件回弹后的张开角α、板料圆角半径R如表4所示。可以看出:和弯曲实验结果对比,Abaqus有限元方法计算的α相对误差为4.7%,R相对误差为8.7%;而采用SFS-SVM算法的α相对误差为1.6%,R相对误差为6.9%。基于64核的CPU,进行一次Abaqus有限元计算需时为1 h 13 min 48 s,SFS-SVM算法需时12 min 13 s,时间成本远低于Abaqus有限元计算,并且精度也可以得到保证。

图7 弯曲实验获得的零件
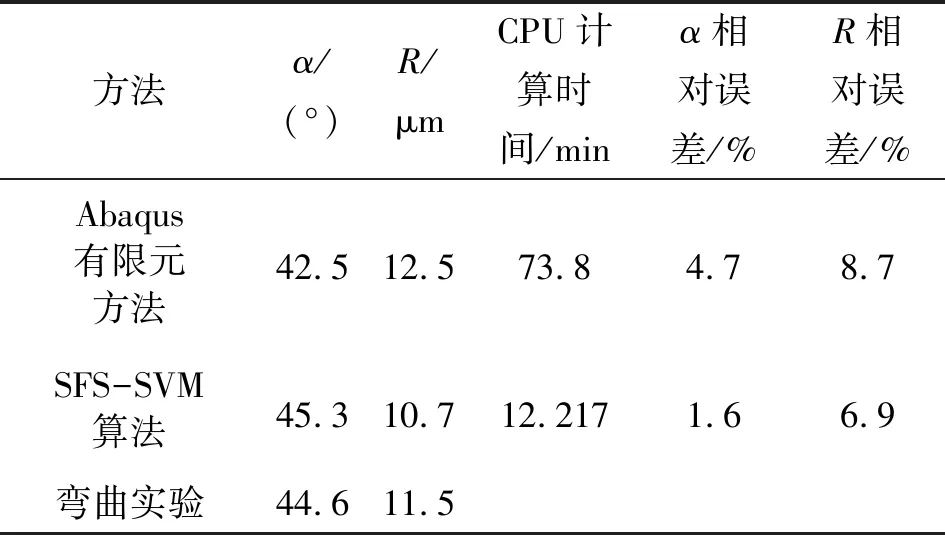
表4 不同实验方法测得的张开角α和R的结果对比
5 结论
工件尺寸和力学性能等诸多因素使得V形工件的弯曲回弹难以预测。以板料回弹后的张开角α和弯曲回弹半径R为目标函数,采用支持向量机(SVM)模型部署到顺序向前筛选算法(SFS)中以高效筛选出最优的特征变量参数子集,从而使构建出来的弯曲回弹模型具有较高的预测精度。
