仿生鲔科机器鱼多机体协同起动性能研究
2022-09-22李家坤张开升张保成
李家坤,张开升,赵 波,张保成
(中国海洋大学工程学院,山东 青岛 266100)
1 引言
仿鱼类水下推进装置的研究大大提高了现代水下机器人的功能,越来越多的研究把目光聚焦在鱼类上。然而,如何有效地研究鱼体关键设计参数对游动性能的影响规律是亟待解决的问题。
有关鱼类游动机理的研究,国内外已取得丰富的成果。文献[1-2]以细长水生生物为研究对象提出了“细长体理论”和“大摆幅细长体理论”。文献[3]提出了“二维波动板理论”来描述带有鳍的鱼类游动。在游动机理研究成熟的基础上,人们开展了对机器鱼样机设计与制作的研究。文献[4]等建立了四关节仿鲹科机器鱼的动力学模型并对其快速起动状态进行了运动规划。文献[5]利用表面镀有超磁致伸缩材料的合金薄板模拟鱼尾,建立力学模型并进行了数值模拟,达到了通过控制外磁场实现机器鱼快速起动的目的。文献[6]采用弹性材料研制出了一款能够模拟鱼类肌肉刚度和阻尼特性的柔性机器鱼样机。文献[7]通过对四自由度仿生机器鱼UC-Ika 1的水动力分析,导出运动控制方程,求解得到机器鱼的巡游速度为0.29m/s。文献[8]应用Udwadia-Kalaba理论对两关节仿鲹科推进模式机器鱼的动力学进行分析,仿真结果表明增加尾鳍摆动幅值和摆动频率可以有效地提高机器鱼的瞬时加速度。文献[9-10]结合牛顿-欧拉法与浮动框架法建立了一种新的机器鱼动力学模型,文献[11]采用递归牛顿-欧拉算法对机器鳗鱼进行了动力学分析。文献[12]提出了一种串联结构来模拟鱼类的变刚度游动,并通过数值仿真得到鱼类的游动性能与摆动频率、身体刚度和斯特鲁哈尔数有密切联系,其结果与生物观察结果一直。文献[13]用曲柄连杆机构模仿胸鳍摆动为仿生鱼提供动力,为仿生鱼的结构设计提供了一种新思路。前人已经对仿生机器鱼开展了大量研究,但仍然存在一些问题:一方面主要通过实验获取鱼类游动的关键参数,在误差控制和节省时间及资源成本方面存在很大缺陷;另一方面没有考虑鱼体与外部环境的流固耦合作用,因此现有的仿生模型与生物鱼类尚有较大差距。
针对以上不足,基于牛顿-欧拉法将鱼体离散为包括胸鳍在内的多个部分建立动力学模型。然后,基于遗传算法工具箱以起动加速度为目标进行优化,以提高多参数协同下机器鱼的起动性能。
2 鲔科鱼类的运动学特征概述
鲔科鱼类高效的游动效率归结于流线型的鱼体、较大展弦比的尾鳍以及其他鱼鳍的共同配合。在此基础上,将仿生鱼模型分为三个部分:胸鳍、尾鳍及鱼体[13],如图1所示。
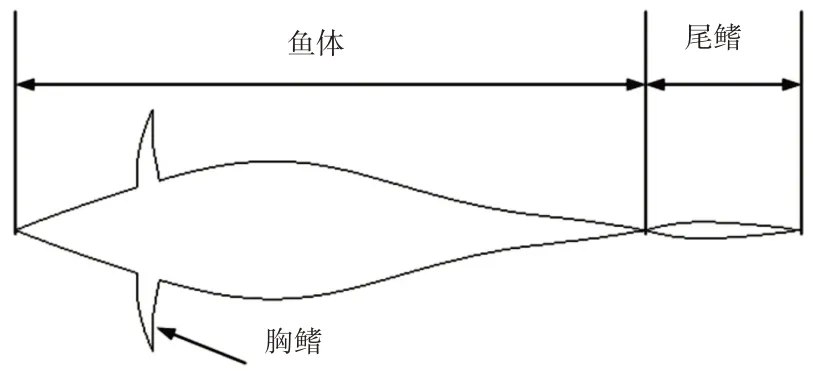
图1 模型简化Fig.1 Model Simplification
2.1 鱼体波动推进的运动学分析
鱼体的波动推进,可看作一列具有特定波长和频率的行波沿鱼体轴线从前向后传播的过程[13]。根据鱼体游动情况,鱼体波为一波幅逐渐增大的行波系列,由一个二次多项式和正弦曲线合成来近似:

式中:yb—鱼体运动方向上x处t时刻的侧向位移;
c1—线性波幅;c2—二次波幅包络线系数;
ω—鱼体波动的角频率;k—鱼体波波数。
2.2 鱼鳍摆动的运动学分析
在鱼类的起动运动中,胸鳍只起到保持鱼体平衡的作用,因此为简化模型,使胸鳍保持恒定击水角度,尾鳍摆动运动示意图,如图2所示。
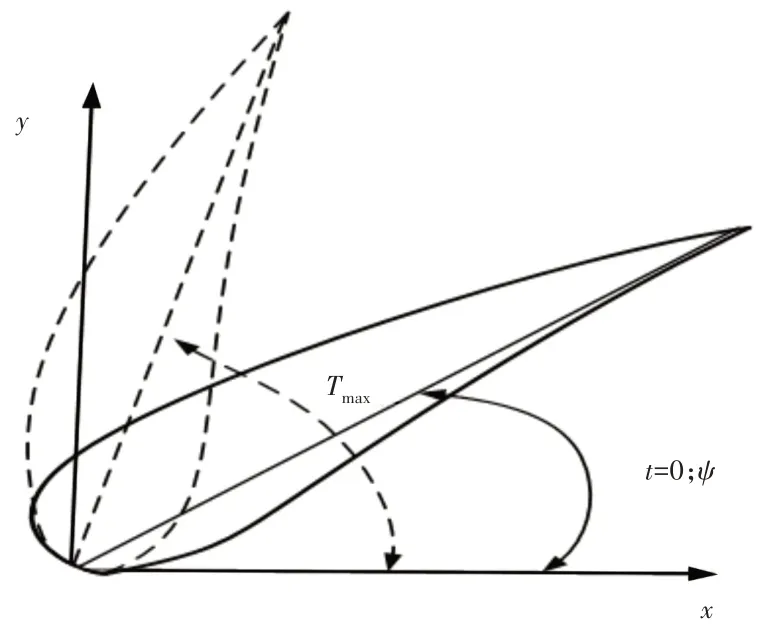
图2 尾鳍摆动运动示意图Fig.2 Caudal Fin Oscillating Motion Diagram
尾鳍的复合运动可以分为三个部分:侧向的平动运动、沿前进方向的运动和绕尾柄的摆动运动。其中—尾柄前段鱼体的推进速度,尾柄的波动运动为ybc(t)=(c1L2+c2L)sin(ωt-kL),尾鳍绕尾柄的摆动与平动运动存在一定的相位差φ。因此,可以用式(2)描述尾鳍的运动

式中:θc—尾鳍与x轴的摆动角度;Tmax—尾鳍摆动的最大幅值。
3 基于牛顿欧拉法建立动力学方程
3.1 坐标系的定义
根据上文对外形特征的分析,将鱼体划分为n个部分,分别为鱼头部分(B1)、鱼体关节部分(Bi(i=2…n))、尾鳍部分(C)及胸鳍部分(P1、P2)。仿生鱼各个部分通过铰接连接,并以Oi(i=1…n-1)表示,其中鱼头绕O1旋转,鱼体绕Oi(i=2…n-1)旋转。各关节质心与上端铰链的距离为ri。
根据需要分别建立大地坐标系S,鱼体坐标系IB及各关节的坐标系Ij(j=1…n)。上述坐标系均符合右手法则且z轴指向鱼体上方。其中,鱼体坐标系原点OB与O1点重合,OBxB指向鱼体运动的反方向,OByB沿水平面指向鱼体右侧;各关节坐标系随鱼体各部分运动,原点Oi与铰链固连,Ojxj沿各个杆单元指向下一个铰点,Ojyj垂直于各个杆单元。不考虑垂直方向上的俯仰运动。鱼体坐标系相对大地坐标系的三维速度、角速度在鱼体坐标系分别表示为(VxVyVz)T、(ωxωyωz)T。另外,定义各关节角速度为坐标系的定义,如图3所示。
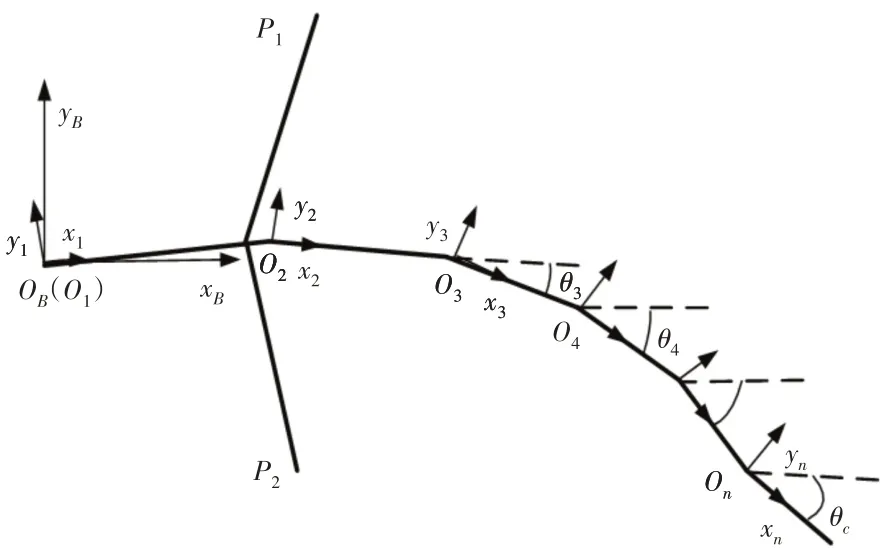
图3 坐标系定义Fig.3 Coordinate Definition
使用ZXY欧拉角ϕ、φ、ψ来描述大地坐标系与鱼体坐标系间的转换。另外,定义Ri为各关节坐标系与鱼体坐标系之间的转换矩阵,如下所示:

3.2 杆单元的运动分析
根据简化的模型和建立的坐标系,设定各个杆单元的的运动定义为:
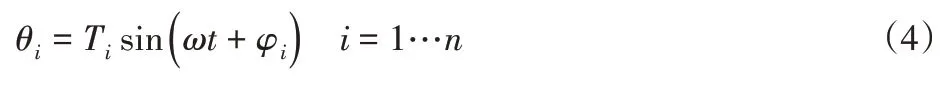
式中:Ti—第i个杆单元的摆动幅值;φi—第i个杆单元与第i-1个杆单元的相位差,特别的φ1=0。
各杆单元相对于大地坐标系的角速度在鱼体坐标系IB中可以描述为:
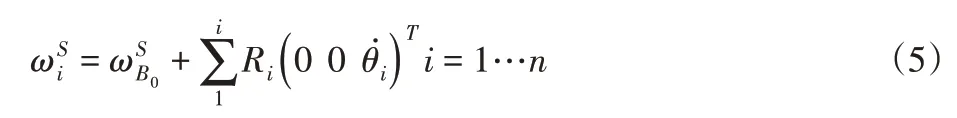
各杆单元的质心相对于大地坐标系的速度在鱼体坐标系IB中可以描述为:
各杆单元相对于大地坐标系的角加速度在鱼体坐标系IB中可以描述为:
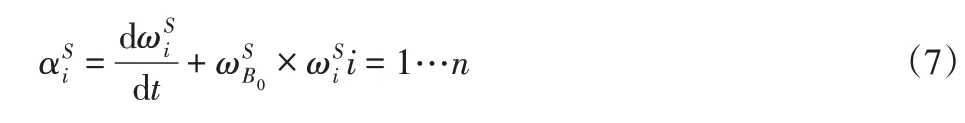
鱼体坐标系相对于大地坐标系的加速度在鱼体坐标系IB中可以描述为:

则各杆单元的质心相对于大地坐标系的加速度在鱼体坐标系IB中可以描述为:
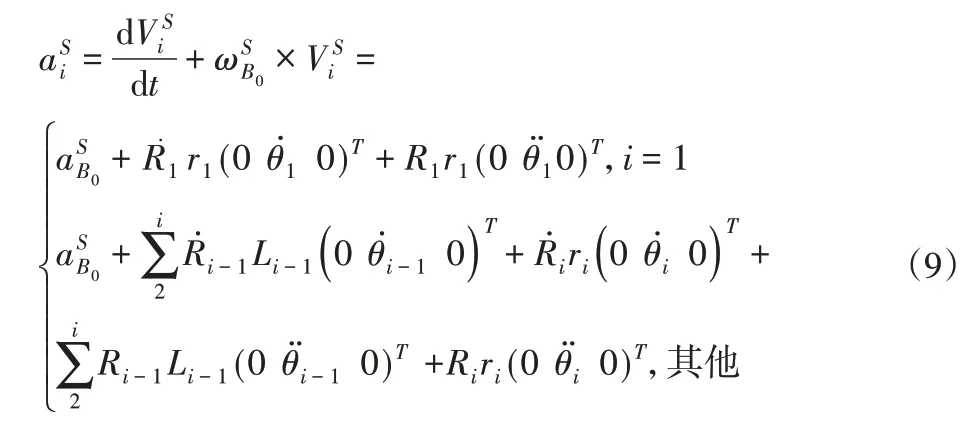
3.3 杆单元的受力分析
结合前人的结论[14]以及前文的概述,考虑仿生鱼游动受到来自重力场、周围流场和鱼体内部的相互作用。
3.3.1 重力和浮力
由于不考虑鱼体的俯仰运动,故竖直方向上的受力平衡。因此,在鱼体坐标系内,第i个杆单元的受力可描述为:

式中:Gi—第i个单元所受重力;Ffi—第i个单元所受浮力;mi—第i个单元的质量;Vi—第i个单元的体积;ρ—流体密度;g—重力加速度。
3.3.2 附加质量效应
附加质量效应可由鱼体的附加质量描述,各环节的附加质量可表示为:
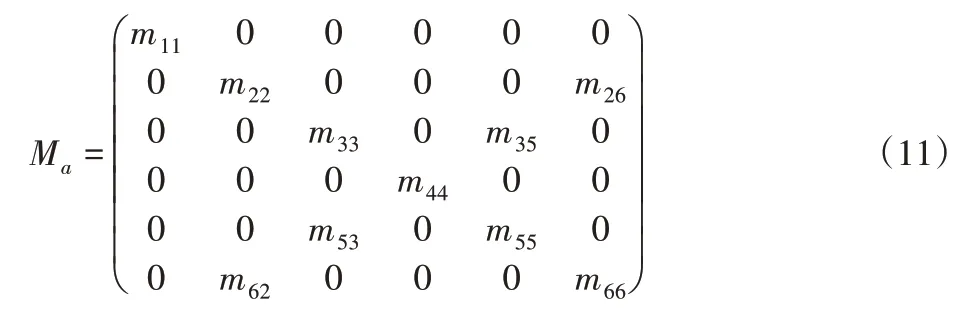
3.3.3 胸鳍升力和阻力
胸鳍受力示意图,如图4所示。
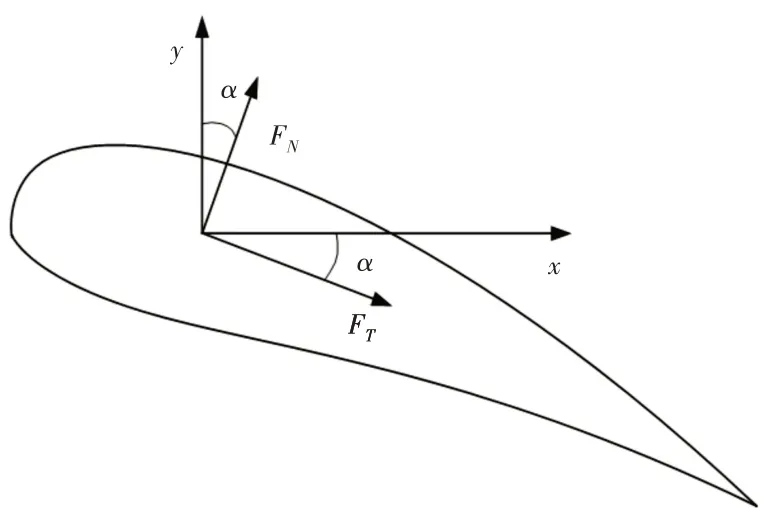
图4 胸鳍受力示意图Fig.4 Force Diagram of Pectoral Fin
通常将胸鳍近似成为机翼,因此单个胸鳍所受到的力可以描述为以下式(12)、式(13)的形式;当胸鳍击水角度为α时,可将受力合成为沿鱼体方向和竖直方向的阻力和升力,如式(14)所示。

式中:FN、FT—单个胸鳍上的法向力和切向力;Vp、Sp—胸鳍速度和面积;CN、CT—胸鳍的法向力系数和切向力系数。
3.3.4 尾鳍升力和阻力
假设尾鳍为一简易刚性平板。尾鳍受力状况,如图5所示。
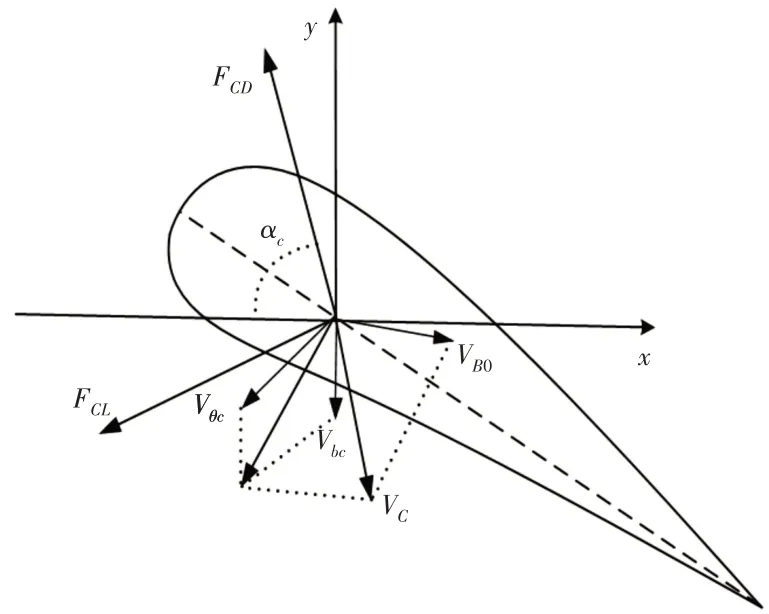
图5 尾鳍受力示意图Fig.5 Force Diagram of Caudal Fin
则鱼体所受升力阻力FcL、FcD可表示为:

式中:CcL—升力系数;CcD—阻力系数;Vc—尾鳍质心的法向速度;Sc—尾鳍迎流面积。
进一步可得到尾鳍在鱼体运动方向和竖直方向上的分力:
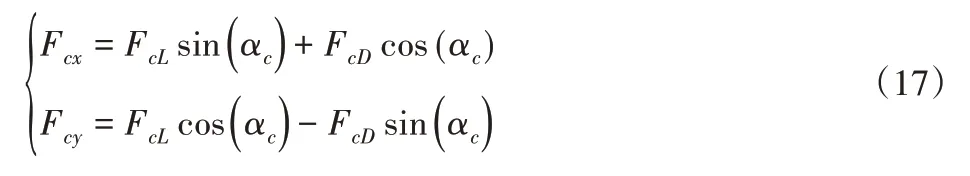
式中:αc—流体速度与水平方向的夹角。
3.3.5 鱼体阻力
可以将鱼体受到的流体阻力描述为:

式中:CDxi、CDyi—第i个关节的x、y方向上的阻力系数;Vxi、Vyi—第i个关节的速度在x、y方向上的分量;Sxi、Sxi—x、y方向上的迎流面积。
3.3.6 鱼体内部的相互作用力
鱼体各个杆单元之间还存在一相互作用的力Fi i-1与力矩,如图6所示。
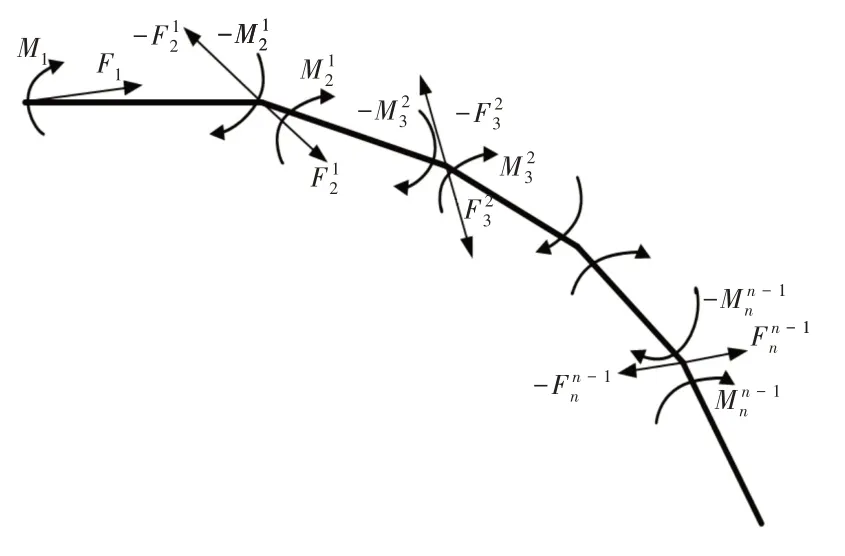
图6 各环节相互作用力与力矩Fig.6 Interaction Forces and Moments
3.4 建立动力学方程
牛顿-欧拉法具有思路清晰和便于编程的特点,由基于经典力学中的牛顿第二定律建立的牛顿方程和欧拉方程组成,根据中间连杆上的力、力矩平衡来描述各部分之间的速度和力之间的关系。建立任意关节的牛顿欧拉方程:
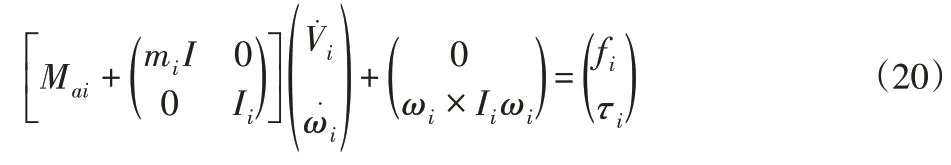
式中:Mai—第i个关节的附加质量;mi—第i个关节的质量;I—单位阵;0—0矩阵;Ii—第i个关节惯性张量;fi、τi—第i个关节外力与外力矩。
对于一个确定的运动状态,可以通过向外迭代得到各个单元的运动参数。由于尾鳍处于自由端,所以受到的力和力矩可知,因此可以通过求解鱼体自由端的动力学方程,进而完成向后的迭代求解,从而得到整体的动力学特征。
4 基于遗传算法的优化设计
遗传算法(Genetic Algorithm,GA)是一种模拟生物界进化法则演化而来的随机全局搜索算法,起源于对生物系统进行的计算机模拟研究。它通过模仿自然界生物优胜劣汰的进化规律而达到寻优的目的。遗传算法从串集开始搜索,覆盖面积大,具有内在隐并行性与良好的全局搜索能力;采用概率变迁规则寻求最优解,自动获取和指导优化搜索空间,具有自适应性、自组织性和自学习能力。所以遗传算法适合仿生机器鱼多参数协同的优化计算。
自然界鱼类进化出了不同的游动姿态以应对复杂环境。在捕食和逃脱时,鱼类采用C形起动或S形起动状态以达到快速起动的效果。北方梭鱼在快速起动时,可达25倍重力加速度,这为弥补现阶段水下潜器的不足提供了新的思路。仿生鱼起动运动的参数优化可利用遗传算法工具箱求解目标函数进而得到波动方程来实现。起动加速度可以表示为:

式中:u—鱼体加速度;m—鱼体质量;Fx—鱼体总推力,其值等于鱼体附加质量力、鱼鳍升阻力、鱼体阻力在机器鱼游动方向上分量的代数和。
为了获取起动性能较好的波动方程,将鱼体离散为6 个关节,设置最大加速度为目标函数,寻优得到仿生鱼各单元的波动幅值、摆动频率等关键参数。限定第一关节的摆动幅值为0,第二、三关节的摆动幅值小于以保证鱼体始终沿着运动方向加速起动。另外,剩余关节的摆动幅值与相位差φi均小于胸鳍击水角αi小于波动频率ω小于5π。根据机器鱼起动加速的实际情况,设置鱼体游速Vx=0,时间t=0。则优化问题可以描述为:
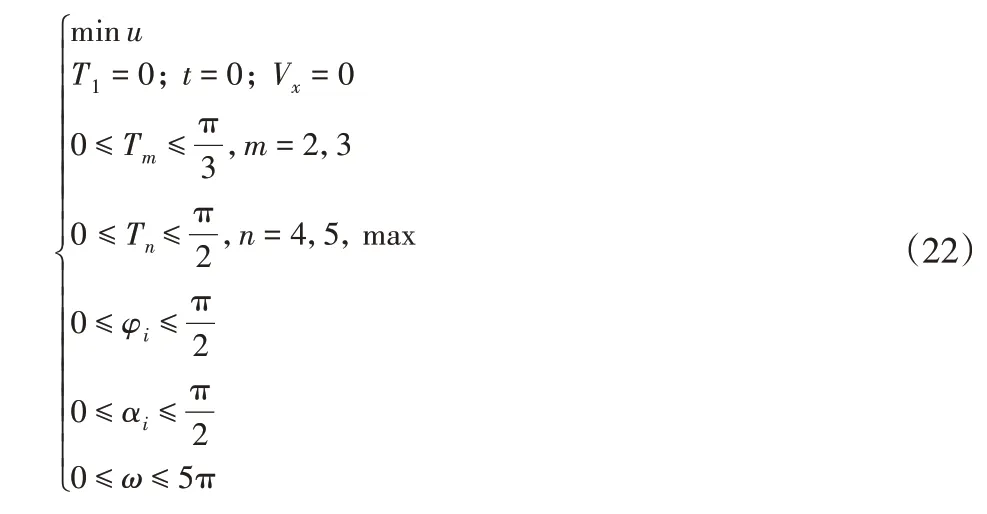
得到的优化结果,如图7、图8所示。
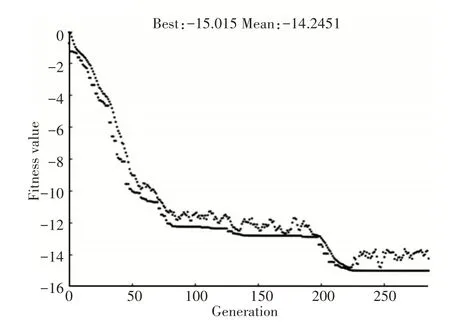
图7 最大起动加速Fig.7 The Maximum Start Acceleration
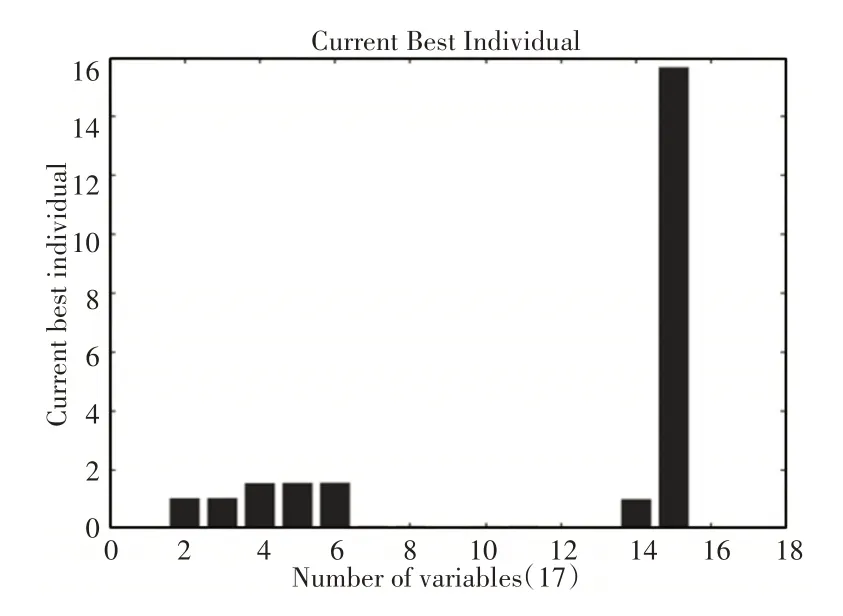
图8 最佳运动参数Fig.8 The Optimum Kinematics Parameters
最大起动加速度u=15.01L/s2,各环节摆动幅值Ti、相位差φi、胸鳍击水角αi、角频率ω分别为:T1=0;T2=1.028;T3=1.035;T4=1.541;T5=1.552;Tmax=1.554;φ2=0.064;φ3=0.063;φ4=0.054;φ5=0.061;φ=0.066;α1=0.002;α2=0.003;L=1;ω=15.693;t=0;Vx=0。机器鱼各关节的运动变化规律,如图9所示。
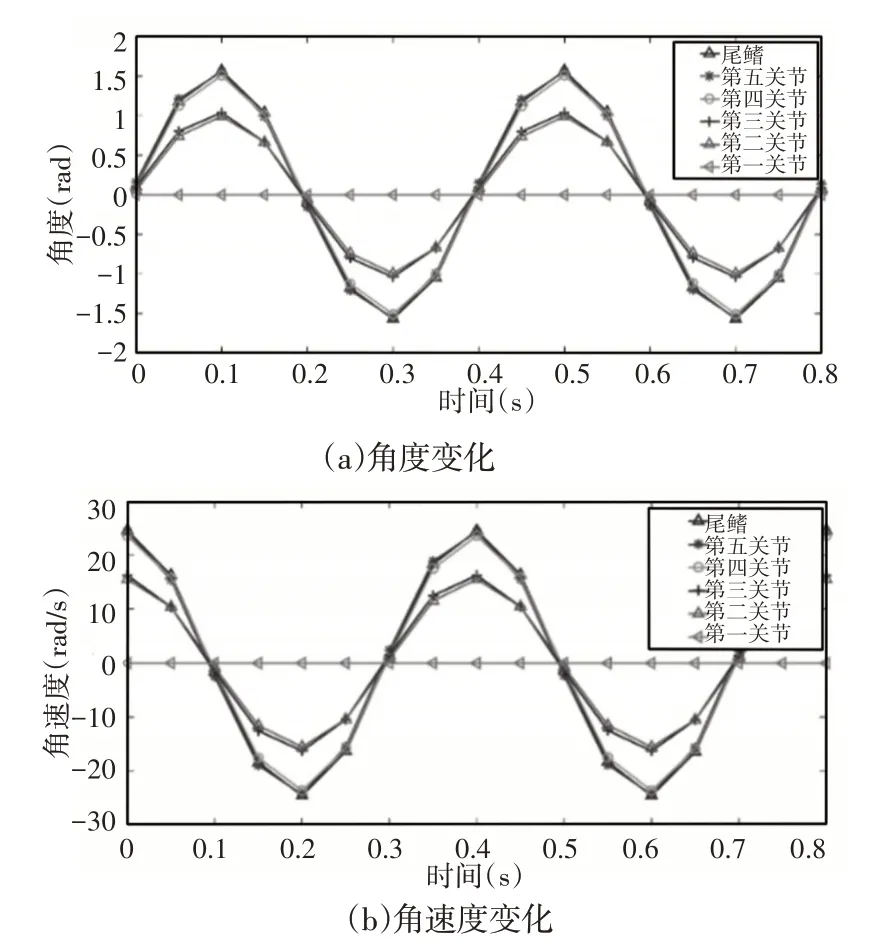
图9 机器鱼各关节运动变化规律Fig.9 Variation Law of Each Fish Robot Link
结合优化结果可以得到以下结论:
(1)各关节角度、角速度均呈现正弦变化规律,当角度的绝对值达到最大值时,该关节处于极限位置,对应角速度变化曲线中的零点位置;(2)鱼体波动频率ω达到极值,尾鳍的优化幅值接近,整个鱼体呈现剧烈的波动状态。实际上,各环节的摆动幅值都接近极值,相对应的,各环节间的摆动相位差都较小,波动具有一致性。这种情况可以解释为:鱼体推进力与波动速度正相关。各环节的大摆动幅值和运动的一致性,使鱼体和尾鳍波动在同一时间总体达到最大,进而通过极大的鱼体和尾鳍的波动速度保证最大的瞬时推进力。在0时刻,各环节基本处于平衡位置,角速度数值达到最大,该结果也可与前面的结论相互对应;(3)左右胸鳍击水角分别为0.11°与0.17°,接近0°,差值可解释为优化误差。在不做单独运动情况下,胸鳍只提供一个阻力,所以要达到减少阻力的效果必须使胸鳍的击水角为0°;(4)机器鱼起动状态基本上可认为是C形起动,这与预期结果是一致的。在鱼类的两种起动方式中,S形起动提供数周期持续的推进力,而C形起动提供一个瞬时极大的推进力。在其他条件相同情况下,C形起动产生的推进力的幅值大于S形起动。本研究考虑的是单一时间点的瞬时推进加速度,因而C形起动无疑更接近优化目标。
经重新拟合,获取鱼体的波动方程为:
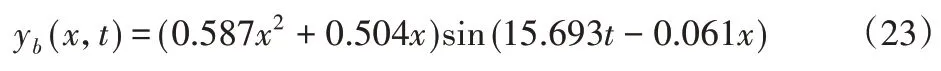
尾鳍的摆动方程为:
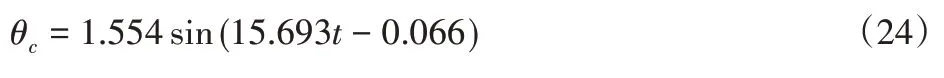
5 数值仿真验证
对前文得到的仿生鱼起动游动进行数值模拟,以验证多机体协同优化方法的有效性。
设置仿真模型整体长度为1m,其中尾鳍部分为0.23m,胸鳍弦长为0.156m,计算域为(8×4)m的不可压缩粘性流体,鱼体起动速度为0m/s,计算得到仿生鱼的推进力随时间的变化情况,如图10所示。
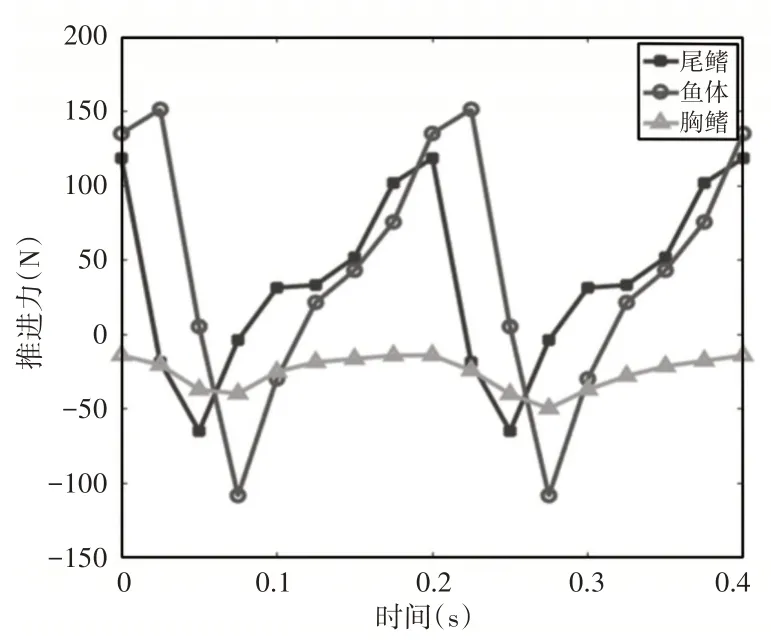
图10 各机体推进力变化规律Fig.10 Variation Law of Multi-Body Propulsion Force
从图中可以看出:各机体产生的推进力都接近周期性变化,变化周期为运动周期的一半。鱼体是最主要的推进装置,尾鳍是次要推进装置,胸鳍在整个过程中都产生阻力。从整个周期的角度来看,机器鱼整体运动在某些时刻会产生阻碍鱼体前进的“负推力”效果。由机器鱼动力学结果可知,鱼体的整体运动参数对鱼体推进力都有影响,其中波动频率ω和尾鳍摆动幅值Tmax是影响机器鱼推力幅值最主要的参数。通过讨论波动频率ω和尾鳍摆动幅值Tmax对加速性能的影响验证优化结果的有效性。参数的选择如下对应不同波动频率和尾鳍幅值时机器鱼的推进力变化情况,如图11、图12所示。可以看出:随着波动频率的增加,机器鱼的推进力幅值也随之增加,考虑到快速起动的过程和作用时间,增加鱼体波动频率对起动加速性能的提高有积极的影响;同时,与波动频率的影响相似,推进力幅值随着尾鳍摆动幅值的增加而增加,这与多机体协同优化的结果一致。但需要注意的是,提高波动频率与摆动幅值会造成机器鱼“负推力”幅值和作用时间的增加,影响机器鱼的推进效率。因此在起动完成后,应重新规划机器鱼的运动。
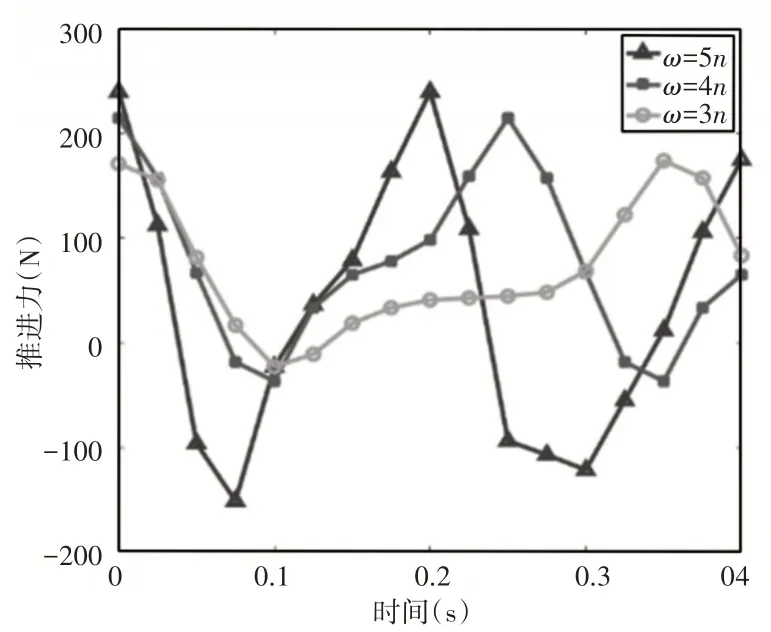
图11 不同频率机器鱼推进力变化Fig.11 Variation Law of Multi-Body Propulsion Force with Different Frequency
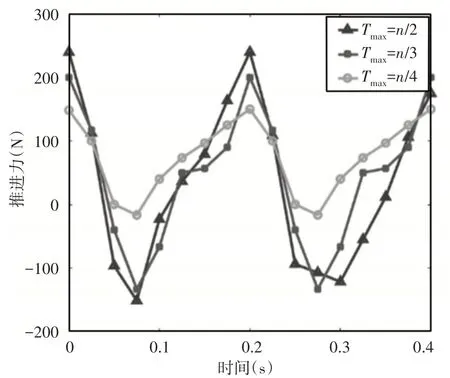
图12 不同尾鳍幅值机器鱼推进力变化Fig.12 Variation Law of Multi-Body Propulsion Force with Different Caudal Oscillating Amplitude
6 结论
应用牛顿-欧拉法和遗传算法构建了鲔科仿生机器鱼的动力学优化模型,并通过仿真验证了该方法的有效性,获取了起动运动姿态的关键参数规律如下:
(1)保证胸鳍击水角为0°;(2)鱼体各关节和尾鳍的波动幅值和角频率应尽可能大,选择的相位差应使各环节波动具有的一致性,实现机器鱼整体波动速度在同一时间点达到最大值。
优化得到的波动方程符合鲔科鱼类起动运动的游动姿态,证明了遗传算法在仿生机器鱼多机体协同参数优化研究方面的可行性,为仿生机器鱼的样机设计和实验研究提供理论依据。
