随机载荷作用下机构关键部件的疲劳寿命预测

邹姗姗，金嘉琦，王显荣，戚基艳

（1.沈阳工业大学机械工程学院，辽宁 沈阳 110870；2.辽河油田青海分公司，青海 德令哈 816000）

1 引言

疲劳寿命的预测方法主要集中于恒幅载荷和载荷加载次序的研究上，对于随机载荷作用下的疲劳寿命研究往往被忽略，而作为特种车辆在工作过程中往往承受随机载荷应力的加载，因此研究随机载荷作用下的机构疲劳寿命预测方法具有特殊意义。

舰载机牵引车作为承受随机载荷的特种车辆，可以依靠自身能力来实现舰载机稳定的移动和精准的停放[1]。举升机构举升轴作为舰载机牵引车主要承载部件之一，其疲劳寿命的大小既反映了自身的疲劳可靠性，又在一定程度上影响到举升机构和整车的可靠性，因此以随机载荷作用下举升机构举升轴的疲劳寿命为研究对象对研究随机载荷作用下机构的疲劳寿命预测方法研究具有实际意义。

疲劳寿命一直以来作为国内外学者关注的热点问题，文献[2]介绍了一种ESO的优化方法对三维结构模型得到的疲劳寿命进行优化设计；文献[3]在该模型结构上为了分析其危险部位的疲劳寿命，提出了一种模型是关于多轴疲劳寿命分析；文献[4]验证了等效结构应力法对结构寿命估算的适用性；文献[5]根据车架实际承受载荷和路面激励情况计算关于车架的疲劳寿命。但目前对于随机载荷作用下的特种车辆关键部件疲劳寿命的研究在国内还是一片空白。

为了研究随机载荷作用下机构的疲劳寿命方法研究，以舰载机牵引车举升机构举升轴的疲劳寿命预测为例，结合理论、实验与仿真，最后构造出关于随机载荷作用下的举升轴疲劳寿命数学模型，得到关于举升轴的疲劳寿命。

2 基于ADAMS的舰载机牵引车举升机构动力学分析

2.1 舰载机牵引车建模

舰载机牵引车举升压紧机构由两部分组成，即压紧机构和举升机构两部分，如图1所示。

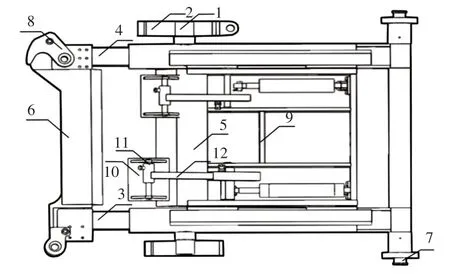
图1 舰载机牵引车举升压紧机构示意图Fig.1 Schematic Diagram of the Carrier-Based Tractor Towing and Boosting Mechanism

其中压紧机构主要起到压紧机轮的作用。举升机构主要是对舰载机机轮进行夹紧和举升，使舰载机牵引车能够更有效率的对舰载机进行牵引。举升压紧机构主要是由举升轴1，斜面滑块2，左伸缩臂3，右伸缩臂4，前臂5，油缸托架6，长轴7，摆动紧扣8，支撑板9，压板10，压板轴11，伸缩杆12等组成。举升压紧机构主要通过举升轴在斜面滑块上的移动，实现举升机构向上举升的过程。

2.2 作用载荷及运动参数

（1）对舰载机牵引车举升机构进行约束添加，结合工况实际添加9 个固定副，2 个移动副，1 个转动副共19 个约束。（2）基于此主要添加了两个约束类型：旋转驱动2 个，滑移驱动4 个，采用step 函数进行定义，举升轴与斜面滑块滑移驱动定义类型为速度：

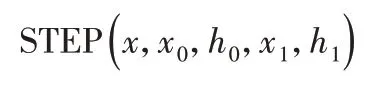
式中：x—变量；

x0，x1—变量的初始值和终止值；

h0，h1—对应x0，x1的函数值。

斜面滑块与地面的滑移驱动速度为定值26.75mm/s并添加外部载荷力force。

2.3 载荷谱仿真计算

在Adams 中建立仿真模型，定义仿真时间为20s，步数为1000步，得到举升机构的载荷时间历程，如图2所示。

图2 举升机构载荷时间历程图Fig.2 Lifting Mechanism Load Ttime History Diagram

3 构建举升轴的疲劳寿命曲线

首先通过Workbench对舰载机牵引车举升机构的举升轴进行仿真，然后在仿真结果的基础上对其试件进行拉伸疲劳试验，最后根据实验结果构建其疲劳寿命曲线（S-N）。

3.1 举升机构关键部件有限元仿真分析

为了构建举升机构关键部件的S-N曲线，因此要对其进行拉伸疲劳试验，其中拉伸疲劳试验的数据是通过对其进行有限元仿真分析得到的。

首先建立举升机构关键部件的有限元模型，其次在Work⁃bench中对其进行模态分析和谐响应分析，举升轴模态分析结果，如表1所示。举升轴谐响应分析结果，如表2所示。

表1 举升轴模态分析结果Tab.1 Lifting Shaft Modal Analysis Results

表2 举升轴谐响应分析结果Tab.2 Lifting Shaft Harmonic Response Analysis Results

3.2 拉伸疲劳试验

目前，针对多数现有的模型，在进行疲劳分析时，往往采用基材的S-N曲线或数学方法修正得到S-N曲线，而不是基于模型实际的S-N曲线进行疲劳分析。

进行疲劳试验的试件是举升机构关键部件的易损部位进行线切割加工得到的，疲劳试件尺寸与形状，如图3所示。相比采用其基材的S-N 曲线或数学方法修正得到的S-N 曲线，构建的S-N曲线考虑到其易损部位并结合举升轴的工况实际，使其疲劳分析的结果更接近实际，更准确。试验试样采用漏斗形试样，试样材料为C45其力学性能，如表3所示。尺寸，如图3所示。

图3 疲劳试件Fig.3 Fatigue Test Piece

表3 试件材料力学性能Tab.3 Mechanical Properties of Test Materials

测定S-N曲线采用成组法[6]，试验所需的仪器设备为电液伺服疲劳试验PA-100。疲劳试验的参数为谐响应分析得到的最大应力，本次试验需要的疲劳试件共18根，每3根疲劳试件为一组，一共分成6组。因此，在室温和标准大气环境，应力比R=0.355，频率为12Hz的条件下进行试验。试验过程，如图4所示。试验数据[7]，如表4所示。

图4 试验过程Fig.4 Test Process

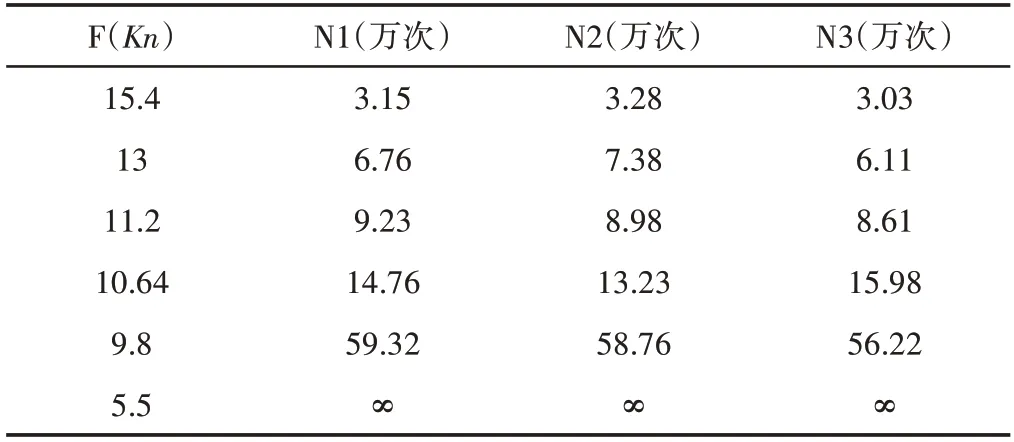
表4 试验数据Tab.4 Test Data

将表4的实验数据输入到origion中，构建出举升机构关键部件举升轴的S-N曲线，其疲劳极限为MPa，如图5所示。

图5 举升轴的S-N曲线Fig.5 S-N Curve of the Lifting Shaft

3.3 载荷谱编制

载荷谱编制以往采用动力学分析得到的时间序列谱直接进行编制，而这里将基于动力学分析软件Adams 得到的时间载荷序列以及根据构件本身得到的S-N 曲线共同进行编制，得到关于举升轴的载荷谱，如表5 所示。从而使其疲劳寿命计算更具有真实性。

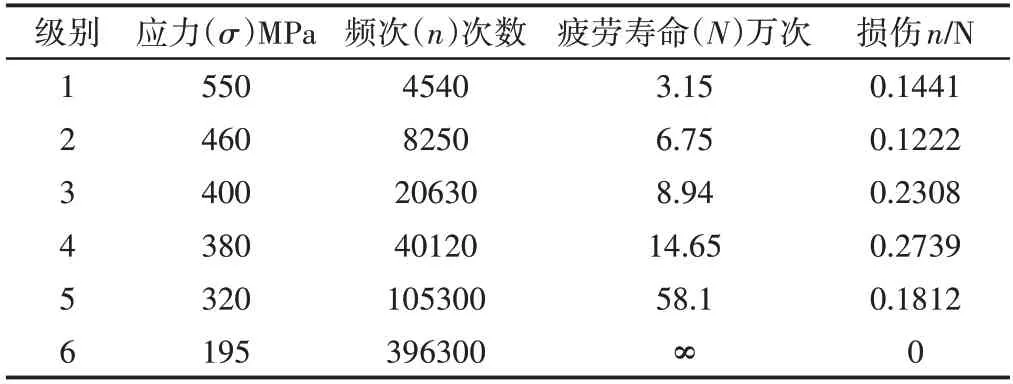
表5 举升轴载荷谱Tab.5 Lifting Shaft Load Spectrum

4 构建随机载荷作用下举升轴的疲劳寿命预测评估模型

4.1 基于模糊理论的概率Miner法则数学模型建立

由工程实际可知，机械构件承受载荷往往具有随机性，针对疲劳寿命的研究理论中，研究载荷主要为循环恒幅载荷或载荷加载次序下的疲劳寿命，对于载荷随机性问题往往被忽略，因此针对特种车辆特殊模型提出随机载荷作用下的疲劳寿命预测模型即基于模糊理论的概率Miner法则[8]。

由舰载机牵引车工作环境及工况条件可知，舰载机牵引车举升压紧机构所承受得载荷为随机载荷，因此将举升轴承受随机载荷作用所引起的应力变化用概率形式进行描述。应力时，概率可以表示为P(σi)，则为：

式中：f(σ)—概率密度函数表示的构件直接作用承受应力大小；g(σ)—概率密度函数表示外界因素影响条件下构件承受的应力大小。

由Miner法则可知将概率密度分布函数划分为k个子区间，则连续性概率密度函数定义下的总损伤D为：

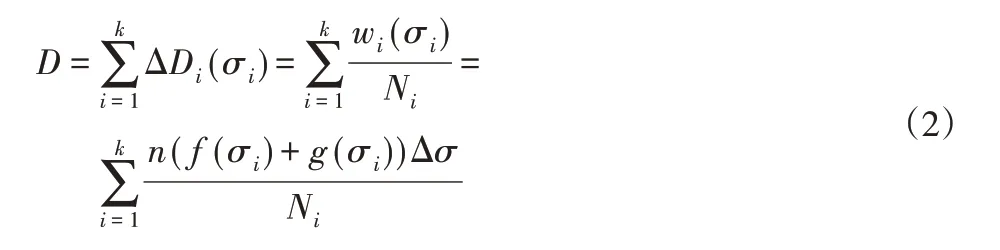
式中：n—随机载荷作用次数；w i(σi)—对应应力发生作用的次数；ΔDi(σi)—构件的疲劳累计损伤。

经查阅文献可知，当应力值大于疲劳极限应力时，可通过S-N 曲线获得其疲劳寿命，因为基本S-N 曲线是在对称应力循环条件下）R=-1）获得的，其曲线斜率上的每一点(σi，Ni)都满足如下公式：

式中：m，C—材料常数；N0—应力循环基数；Ni—第i级应力单独作用产生破坏的应力循环次数；σ-1—疲劳极限。

对于应力比R不等于-1的应力循环，计算疲劳寿命时需要采用goodman法则进行修正即：

式中：σa—平均极差应力；σb—平均应力；R—应力比；σu—最大抗拉强度；σmax—最大应力值；σmin—最小应力值。

由式（4）～式（6）联立求得：

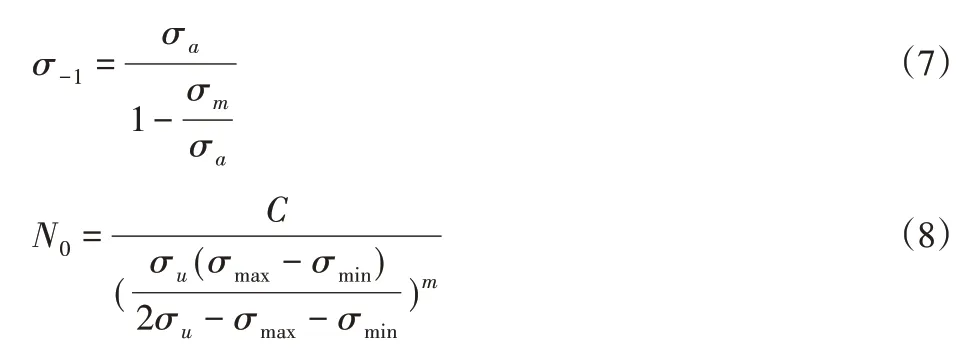
采用指派法对低于疲劳极限的应力所造成的损伤产生的模糊性进行分析。为了便于分析，假设对材料造成的模糊应力集合的上限σr，下限σt，则隶属函数可以定义为：

式中：σt—材料的强度极限。

则可得疲劳寿命模糊性数学模型［9］：

当应力值在疲劳极限以下时，要考虑应力产生疲劳的模糊性，由于概率分布函数的区间分为k个子区间，可设处于模糊域的子区间数为αk，其中0<α<1，由式（2），式（9），式（10）得：

当k→∞时可得：

当构件发生疲劳失效时的累计损伤量D=1，所以由式（11）可知，累积疲劳寿命为：

因此式（12）即为在随机载荷的作用下，疲劳寿命预测的数学模型，由模型可知，只要测出构件的材料参数m，c和随机载荷作用下构件所服从概率密度函数参数h（σ）=f（σ）+g（σ），便可对构件的疲劳寿命进行预测。

4.2 举升轴疲劳寿命计算

（1）举升轴的载荷谱及实验数据，如表5所示。其实际工作参数，如表6所示。

表6 舰载机牵引车的实际工作参数Tab.6 Actual Working Parameters of the Carrier Aircraft Tractor

（2）对表5数据运用matlab软件进行统计学分析，由分析lil⁃lietest（x）结果h=0可知，应力近似服从于正态分布，由正态分布公式可得平均应力µ=384.17，标准差σs=121.18，因此关于应力载荷的概率密度函数：

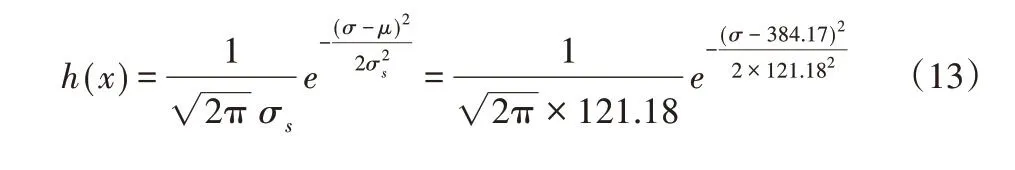
式中：σs—标准差；σ—应力值；µ—平均应力。

（3）计算在不同隶属函数条件下的疲劳寿命，运用matlab函数算法对表5中试验数据进行幂级函数拟合，得到关于材料参数的m和c的数据，即为m=7.38，c=3.6235×1025。

通过matlab对式12和隶属函数进行编程定义得到的疲劳寿命，如表7所示。采用传统的离散型Miner法则进行疲劳寿命估算，计算结果如下[10]：

表7 疲劳累计损伤理论疲劳预测结果及误差Tab.7 Fatigue Prediction Results and Errors of Cumulative Fatigue Damage Theory

误差为：

式中：δ—误差；N—疲劳寿命循环次数；Nr—给定循环次数

4.3 疲劳寿命计算结果分析

根据线性疲劳损伤理论，根据舰载机牵引车的实际工作数据将循环次数换算成时间标定。基于随机载荷作用下的舰载机牵引车举升压紧机构举升轴的疲劳寿命分析得到最小寿命为：≈14.526 年，误差为3.16%。与传统Miner 法则相比较误差降低了30%左右，验证了此方法计算随机载荷作用下的机构疲劳寿命更加精确，更接近举升轴的真实寿命。

5 结论

通过对舰载机牵引车举升机构举升轴疲劳寿命预测与分析，验证了此基于随机载荷作用下机构疲劳寿命预测方法的精确性。对特种车辆在随机载荷作用下的疲劳寿命分析和相关技术研究有着深远意义。

（1）提出基于构件本身的疲劳拉伸实验法，构建出关于构件的S-N曲线，相比于经验或者基于材料本身的S-N曲线更加贴和构件疲劳寿命实际，确保了构件疲劳寿命分析的精确性。（2）提出基于疲劳寿命曲线的载荷谱编制，分析构件动力学时间载荷序列谱，通过与构件本身S-N 曲线共同编制得到关于构件实际运动的疲劳寿命载荷谱，为其疲劳寿命分析提供了数据支持。（3）提出基于模糊理论的概率Miner法则，得到随机载荷作用下疲劳寿命预测数学模型，以舰载机牵引车举升压紧机构举升轴为例，表明其相较于传统Miner法则误差降低了10%左右，可见此预测疲劳寿命方法模型准确性更高。（4）隶属函数的选取对构件疲劳寿命的预测精度影响较大，即当隶属函数为升半Γ分布时，误差更小。为预测随机载荷作用下的特种车辆疲劳寿命提供了研究方法和理论模型，也为其优化改进以及检修维护提供了理论依据。