数控轧辊磨床三点非接触式测量原理及误差分析与仿真

李 阔，吴怀超，令狐克均，赵丽梅

（1.贵州大学机械工程学院，贵州 贵阳 550025；2.贵州装备制造职业学院，贵州 贵阳 551400）

1 引言

随着我国产业结构的调整和产品科学技术的不断发展，行业对轧辊磨床的自动化程度、性能和功能提出了更高的技术要求。特别为提高工作效率，轧机的技术性能不断更新，对轧辊磨床的磨削效率和精度的要求也越来越高。

目前国内数控轧辊磨床普遍采用的两点测量装置不能从多维角度真实反映检测的精度，且两点式测量不能利用误差分离技术将主轴的回转误差与待测轧辊表面信息误差分离开，导致直径测量误差仅能达到0.01mm。在线测量数据由于不稳定只能作为参考，不能参与程序计算，难以对磨削精度的适时修正提供支持。目前国内外学者针对轧辊加工难以实现在线测量、测量精度低的问题展开了很多研究，其中误差分离技术是实现在线测量不可或缺的一环。最早三点法误差分离技术的是文献[6]于1966年提出该理论，该技术自提出之后就得到了国内外学者的研究和企业的广泛应用。

文献[2]结合实际生产条件提出了一种时域三点法误差分离技术，在这里指出时域三点法误差分离技术有更快的计算速度并且其误差与频域三点法误差分离技术相差不多，但由于该方法存在谐波抑制的问题，所以实际应用范围并不广；文献[4]对误差分离技术的算法进行了研究。

提出了一种利用矩阵计算三点法误差分离的算法，但该研究仅对分离算法进行了探讨，并没有提到关于该技术误差的分析；文献[10]对三点法误差分离技术的测量结果的误差来源进行了分析并提出了一种改良方法，但这里分析及推论是基于小型轴类零件，对于轧辊这类大尺寸零件并不适用。

为了解决这些问题，现设计一种数控轧辊磨床的三点法非接触测量方法，利用最小二乘圆法及误差分离技术，分析了误差来源及其对测量结果的影响，并进行了数学推导，根据推导过程建立了测量方法的数学模型，通过Matlab仿真成功分离出了主轴的回转误差与外廓的圆度误差，验证了该模型的正确性。

2 三点非接触测量系统

2.1 最小二乘圆法评定圆度误差

当前圆度误差的评定方法多采用最小二乘圆法，因为该方法有完整的计算方法所以很容易的在计算机上实现，其原理，如图1所示。该方法首先需要计算出最小二乘圆的圆心坐标（a，b）。

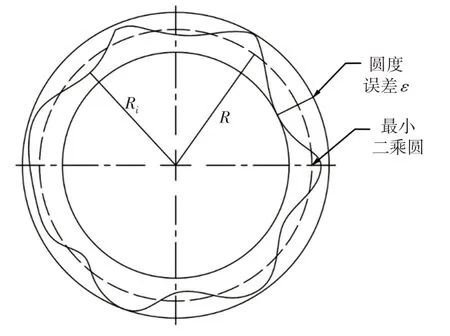
图1 最小二乘法评定圆度误差Fig.1 Least Squares Evaluation of Roundness Error

该坐标的计算方式如下：

式中：xi、yi—待测轮廓上测点处坐标；ri—测点到坐标原点的径向距离；R—最小二乘圆半径；n—选取测点数量，测点越多测量越精准，通过n个测点将圆等分。

求出最小二乘圆的圆心坐标（a，b）后再求出轮廓上各点到最小二乘圆圆心的距离Ri，计算方法如下：

最后计算圆度误差ε，计算方法如下：

2.2 三点测量误差分离

三点法误差分离技术（EST）是实现高精度在线测量的必要条件，其原理，如图2所示。

图2 三点法误差分离原理Fig.2 Three-Point Method Error Separation Principle

由图2示意图可以看到，在待测工件圆周分布着三个位移传感器S1，S2和S3，三个传感器安装时它们探头的延长线交于一点，以该交点为原点建立坐标系xoy，传感器S1在x轴上，传感器S2与S1夹角为α1，传感器S3与S1夹角为α2。

三个传感器的采集数据分别为s1（θ），s2（θ），s3（θ），则有：

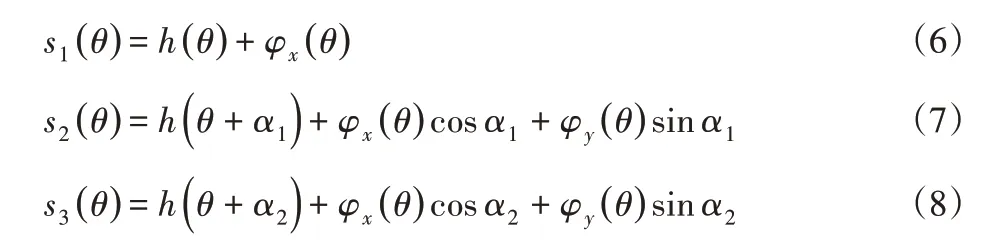
式中：h（θ）—工件圆度误差；ψx（θ）—主轴回转误差在X轴方向分量；ψy（θ）—主轴回转误差在Y轴方向分量。

令三个传感器采集的数据的线性组合为s（θ），每个传感器采集数据乘上权系数c0，c1，c2可得到下式：

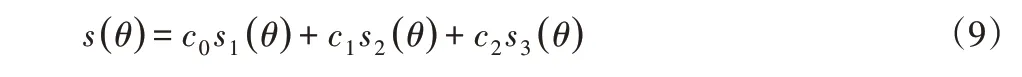
将式（6）～式（8），带入式（9），且令c0=1整理可得：

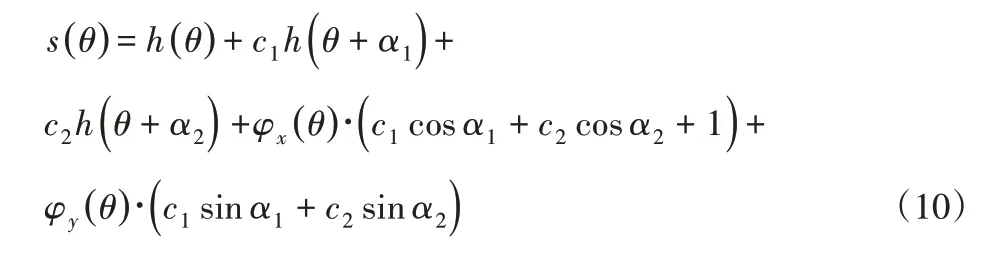
令（10）式中ψx（θ）和ψy（θ）两项的系数为0，可得权系数c1，c2：

对式（9）进行离散傅里叶变换可得：

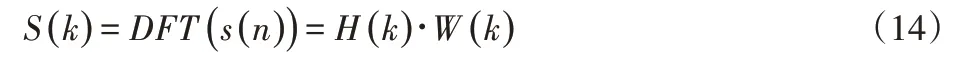
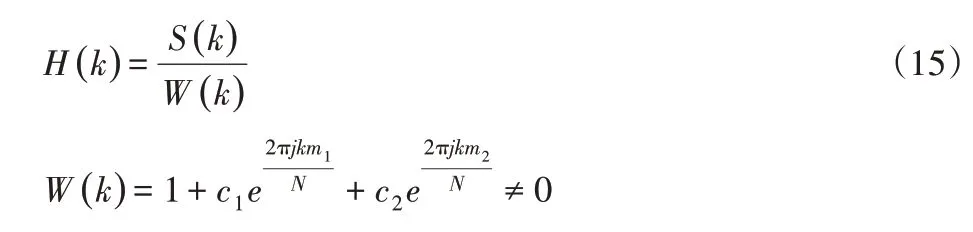
分离回转误差后的圆度误差可由式（13）经过傅里叶反变换求出：

求出圆度误差后将其结果带入式（6）～式（8）三式即可求出回转误差。

2.3 回转运动及偏心运动误差分离方法

因为待测轧辊的外形可以看成是以2π为周期变化的复杂封闭曲线，所以可以用傅里叶级数的方式表示：

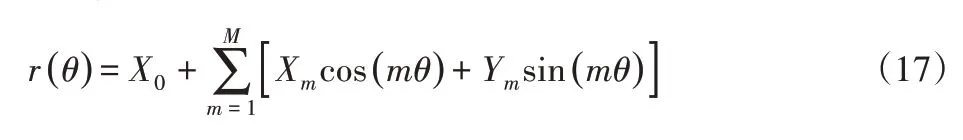
式中：θ—待测轧辊的角度变化；X0—被测轧辊外形的直流分量；M—被测轧辊轮廓的最大谐波阶数；Xm—m阶谐波分量的余弦分量；Ym—m阶谐波分量的正弦分量。

那么可将式（1），式（2）改写为如下形式：

由式（17）我们可以得出待测轧辊的傅里叶级数的一阶谐波分量是最小二乘圆心的偏心运动的结论示意图，如图3所示。

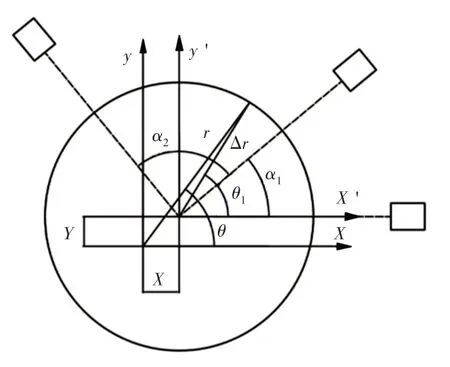
图3 三点法回转运动误差示意图Fig.3 Schematic Diagram of Three-Point Slewing Motion Error

根据示意图给出的几何关系用h（θ1）表示圆度，有以下关系：

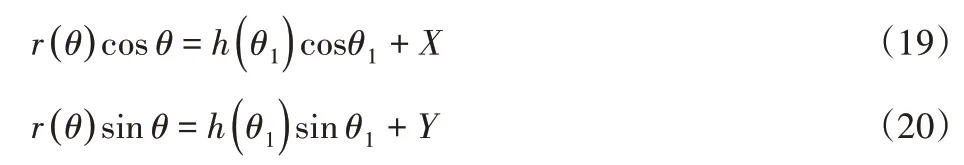
将式（19）乘cosθ加上式（20）乘sinθ可以得到式（21）：

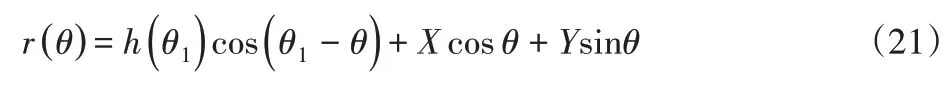
上述推导中我们已知轮廓傅里叶展开的一阶谐波分量为最小二乘圆心的偏心运动，现用Δh（θ）表示除偏心运动外其他项相加和：

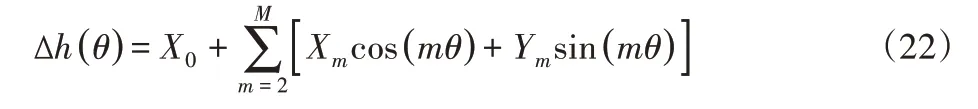
由此可以将被测轧辊轮廓表达写成下式：

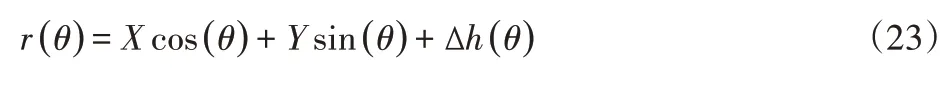
经由式（23）式和式（14）式（16）两式可得到轧辊的圆度误差的离散形式h（n），将式（6）～式（8）离散化并以矩阵的方式表达可以写成下面的形式：

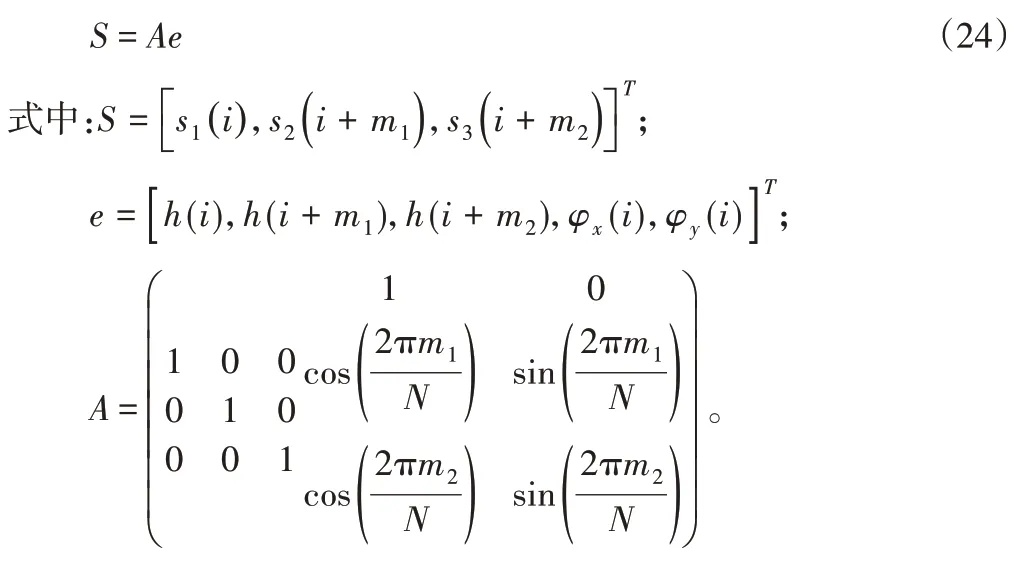
式中：i—测量点按周期转动排序的序列位置，i=0，1，2，3，…，N-1；S—三个传感器的输出组成的矩阵；e—被测轮廓的总误差，包括两个部分，分别为回转误差和形状误差（圆度误差）；A—系数矩阵。

将离散化的圆度误差h（n）带入到式（24）中，联系式（21）的离散形式可以得到：

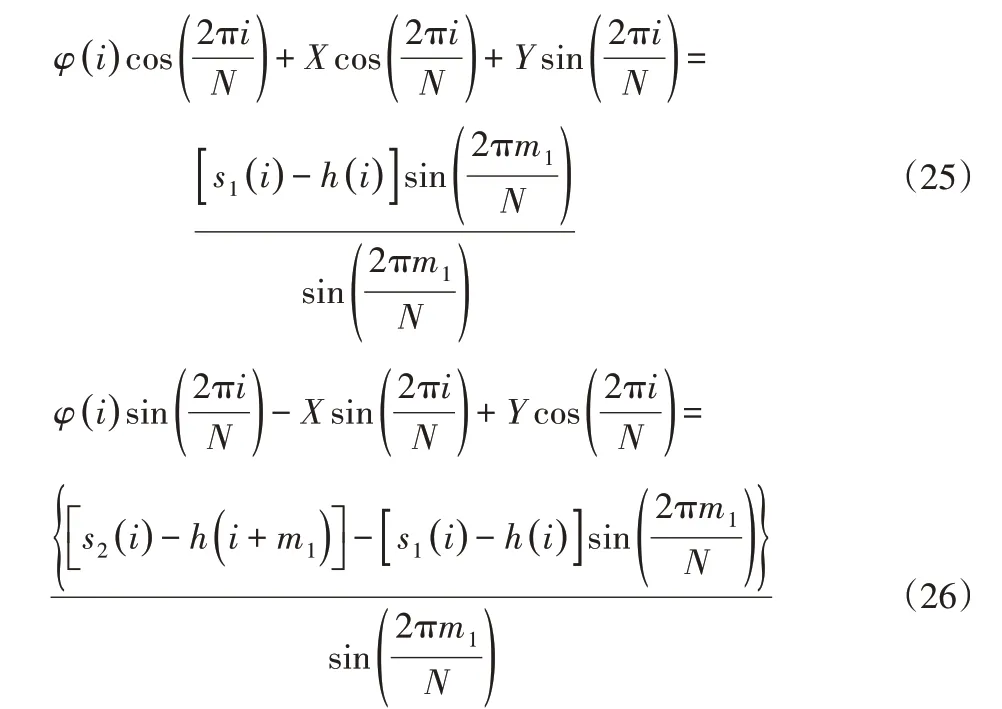
式中：ψ（i）—离散形式的回转误差。

上述两个式子的右边都是已知量所以分别用U1和U2来表示用式（25）乘上sin（2πi/N）减去式（26）乘上cos（2πi/N）并化简可得：

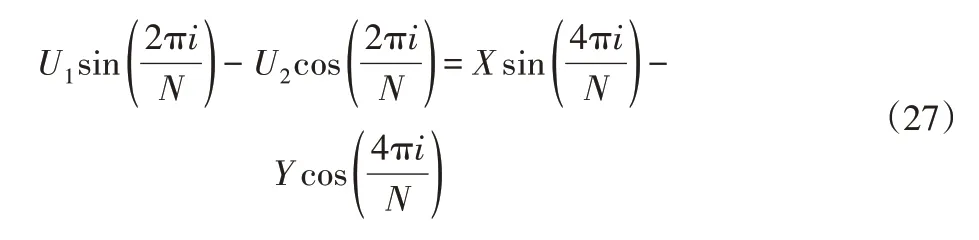
对上式（27）经过化简取均值可以得到回转运动误差及X轴方向分量和Y轴方向分量：

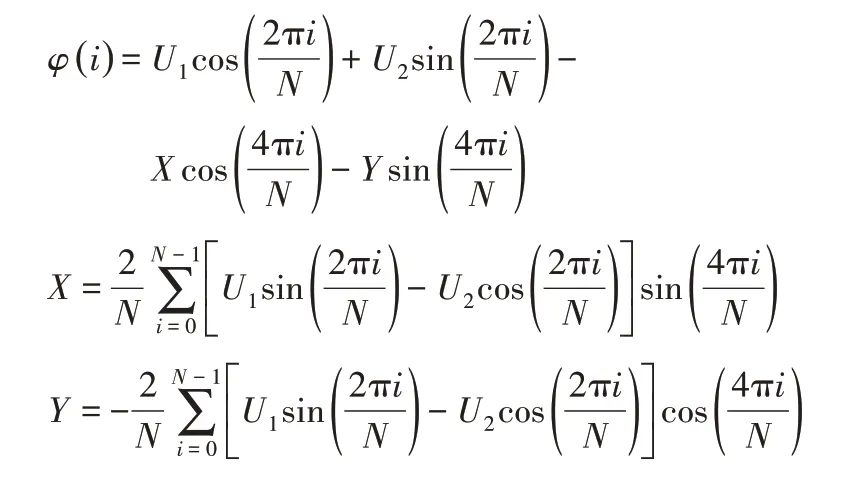
至此就可以将回转运动误差与圆度误差分离并分别求出。

3 三点非接触测量误差分析

3.1 定位夹角误差分析

定位夹角误差指的是传感器在安装固定过程中与预设的探头位置出现了角度为ζ的夹角，假定S2和S3两个探头的误差夹角分别为ζ1、ζ2示意图，如图4所示。

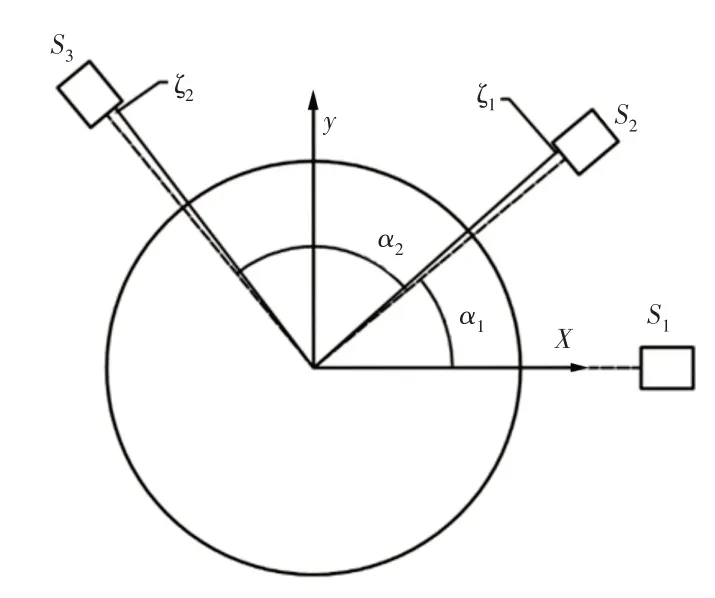
图4 三点法定位误差示意图Fig.4 Schematic Diagram of Three-Point Positioning Error

此时传感器的采集数据的方程组可表示为：

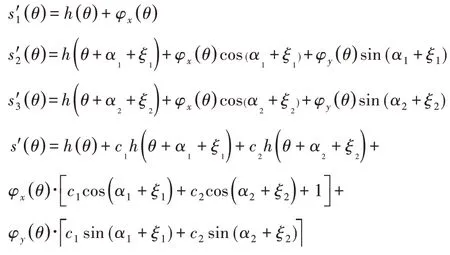
令误差值为η（θ），与式（10）联立化简并假设ς1=ς2=ς，即可得到下式：

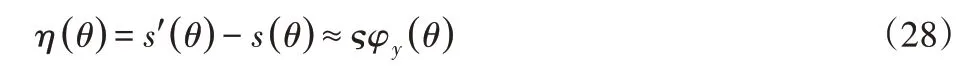
3.2 传感器角度错位误差分析

传感器角度错位指的是安装好的传感器之间实际夹角与预设的α1和α2不一致，导致权系数矩阵偏离预设值出现误差从而使圆度误差与回转误差无法分离，其示意图，如图5所示。

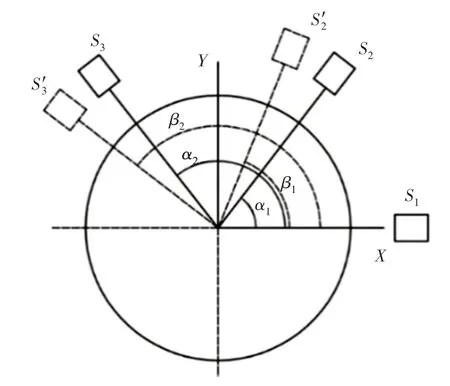
图5 传感器角度错位示意图Fig.5 Schematic Diagram of Eensor Angle Misalignment

所以在安装角度的选择上要充分考虑测量系统安装条件的限制和分离计算条件两个方面，因此我们选取的m1与m2应满足互质的条件且为两个奇数[2]。

4 建模与仿真验证

4.1 误差分离仿真测试

圆度误差分离的仿真原理，如图6所示。预设轧辊轮廓圆度误差的傅里叶展开式：

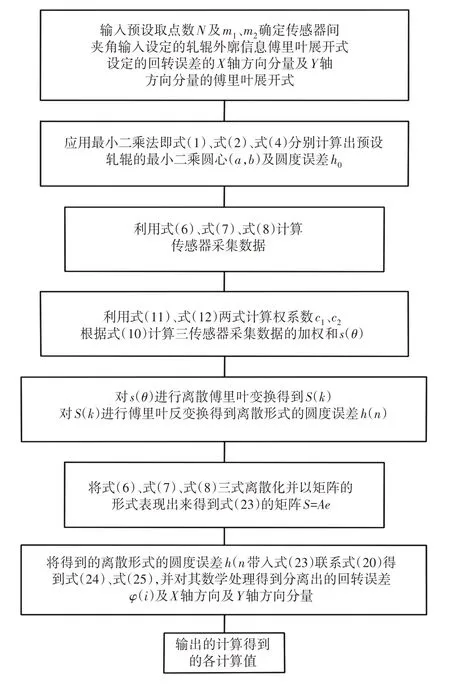
图6 仿真原理流程图Fig.6 Simulation Principle Flow Chart

轧辊的半径设为3，m1和m2要为互质的两个奇数，分别选取为43和121，定位夹角误差ζ设为0.5°，采集点数量N为了保证测量准确性并考虑到加工时的主轴转速，为了让仿真结果更接近实际情况N选取为512。

三传感器接收数据的仿真结果，如图7所示。图7三图显示的是三个传感器S1、S2、S3采集数据的仿真图像，接受的信息包括预设的外廓信息和回转误差。

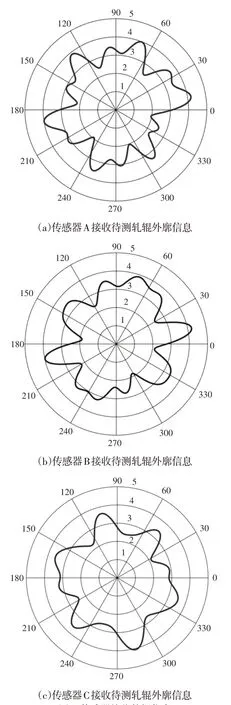
图7 传感器接收数据仿真Fig.7 Sensor Receiving Data Simulation

经过误差分离后的轧辊外廓信息和预设的外廓信息，如图8所示。回转误差和预设的回转误差，如图9所示。

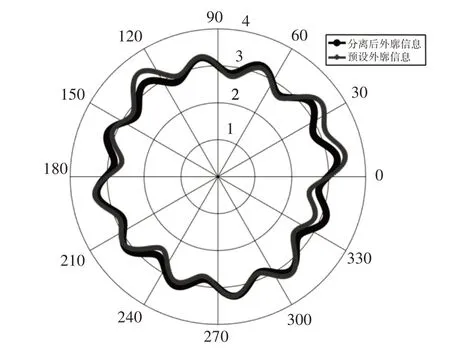
图8 误差分离后轧辊外廓信息Fig.8 Roll Profile Information After Error Separation

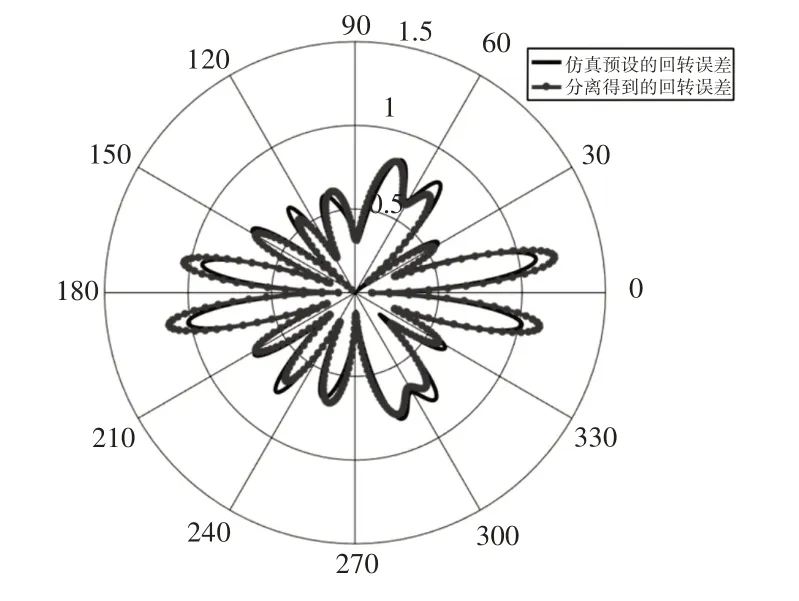
图9 分离前后主轴回转误差Fig.9 Spindle Rotation Error Before and After Separation

从图中线段的对比可以看出误差分离效果很好，基本可将回转误差从采集数据中完全分离出去，残余误差集中在S2传感器和S3传感器安装区域，因为在该部分预设的夹角定位误差ζ 为0.5°，该数据会对测量结果产生一定的影响。

相较与传统两点测量方法，三点非接触测量结合误差分离技术可进一步提升测量精度，其测量精度可达到1μm，并且可以将整体测量误差控制在10%以内，而传统两点接触式测量系统由于无法分离主轴的回转误差其测量精度只能达10μm。由于三点非接触测量不需要与轧辊表面直接接触从而可以实现边加工边测量提高了工作效率并且不会影响轧辊的表面质量。

4.2 定位角度误差仿真

定位角度误差分析的仿真结果，如图10所示。

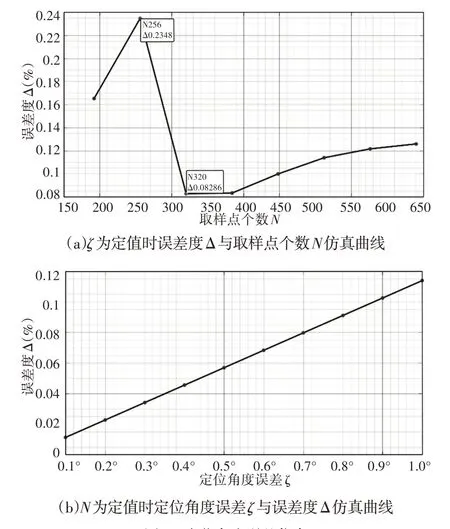
图10 定位角度误差仿真Fig.10 Positioning Angle Error Simulation

仿真测试从两个方面出发分别探究了相同定位角度ζ，不同采样点个数N及不同定位角度ζ，相同采样点个数N对误差度Δ的影响。误差度Δ定义如下式：

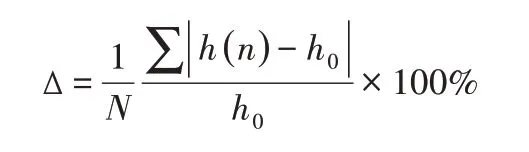
式中：Δ—误差度；h0—利用最小二乘法求得预设的圆度误差。

图10（a）竖轴为误差度Δ，由图可看出定位角度ζ为一定值时，取样点数N取256时，误差度最大达到0.231%，当取样点数N取320时，误差度最小为0.083%。之后随着取样点数逐渐增加，误差度会随之缓慢升高并有稳定在0.122%的趋势。图10（b）仿真曲线可以证明前文中式（27）的正确性，即当我们已知回转误差的Y轴方向分量ψy时，定位角度产生的误差与回转误差的Y轴分量近似呈线性关系，定位角度误差ζ越大，最终的测量误差也就越大，所以在安装传感器时要尽量避免产生定位角度误差。

5 结论

基于matlab平台在三点法圆度误差分离数学模型的基础上分析了三点法测量的误差来源，并建立了定位角度误差对系统影响的数学模型且仿真验证了模型的正确性。

仿真结果证明取样点数N小于256时，误差度Δ随着N的增大而增大；N大于256而小于320时误差度Δ随N增大而减小；N超过320时，误差度Δ随之缓慢升高且有稳定在0.122%的趋势。同时也指出定位角度产生的误差与回转误差的Y轴分量呈线性关系。为数控轧辊磨床的三点法非接触测量系统的设计与研究提供了理论支撑。