典型潮差条件下半潜浮式风机系泊系统设计及动力学特性研究

2022-09-21宋兆波施伟张礼贤李昕王滨

中南大学学报（自然科学版） 2022年8期

宋兆波，施伟,2，张礼贤，李昕,2，王滨

(1.大连理工大学建设工程学部，辽宁大连，116024；2.大连理工大学海岸和近海工程国家重点实验室，辽宁大连，116024；3.浙江省深远海风电技术研究重点实验室，浙江杭州，311122)

近年来，海上风电迅猛发展，截至2020年底，全球海上风电累计装机35 GW，2020年全球新增装机容量6.1 GW，其中我国2020年新增装机量占全球新增量的50%，成为仅次于英国的第二大海上风电市场[1]。目前，中国的海上风电开发主要集中在潮间带和浅海采用单桩固定式基础[2−4]，但随着海上风电研究和开发的不断发展，风机大型化和深远海漂浮式风机基础已成为海上风电发展的两大趋势，我国在建或规划的浮式风电场多位于40～60 m水深的海域，因此，开展中等水深下的大型浮式风机研究具有重要的工程意义。

根据稳定性原理，漂浮式风机主要分为Spar式平台、半潜式平台和TLP 平台，其中Spar 式平台吃水较大，在水深100 m 以内的海域不再适用[5]，而TLP 平台施工安装难度较大，成本较高。半潜式平台是我国漂浮式风电研究和开发的较好选择。漂浮式风机是上部风机、塔架、浮式基础和锚泊系统组成的强耦合系统，且受到风、浪、流等复杂环境载荷的作用。近年来，针对漂浮式海上风机，国内外学者从理论分析、数值模拟及模型试验等多个方面开展了广泛且深入的研究。XU等[6−7]基于Braceless半潜平台，针对50，100 和200 m 水深进行系泊设计，并采用Newman 近似和全QTF 方法进行全耦合数值模拟，发现随水深减小，系泊张力的非线性增强，增设压载块和浮筒能有效改善系泊性能。ZHANG 等[8]利用ANSYS/AQWA 软件分别采用Newman 近似和全QTF方法比较V型平台[9]、BRACELESS[10]和OC4-DEEPCWIND[11]半潜平台在2 个水深(100 m 和200 m)的运动响应，同时考虑黏性阻尼和二阶差频载荷的影响。CAO等[12−13]利用FAST软件同样采用上述2种方法对倾斜立柱式半潜平台进行分析，得出全QTF 方法比Newman 近似更为准确的结论，并进行了相应的模型试验。ZHAO 等[14]基于Braceless半潜平台安装调谐阻尼器(TMD)进行了半潜浮式风机的振动控制研究。

国内外针对潮差问题开展的漂浮式平台研究较少，而中国海域不同于欧洲海域，水深较浅，且潮差问题极为突出。其中，浙江、福建沿海以及台湾海峡地区的潮差较大[15]，以杭州湾为例，上虞码头多年平均潮差达6.14 m[16]，潮差对浮式风机锚链的影响不可忽略。本文作者基于前期设计的新型半潜浮式平台，针对我国典型潮差条件，设计了50 m 水深条件下4 种不同的悬链线式系泊系统。对不同潮位下的静力进行分析，研究潮位变化对平台吃水的影响。同时，采用一体化分析软件Sima，建立耦合时域模型，开展不同系泊方案、不同工况下的风机系统动力特性对比，为我国海上风电工程中的系泊系统设计及优化提供参考。

1 新型半潜浮式风机平台

本文以DTU 10 MW大型漂浮式海上风机[17]为研究对象，自主设计了一款三立柱式钢筋混凝土半潜浮式风机平台[18](图1)，由中柱、3个倾斜侧柱和底部3 个矩形浮筒组成，风机参数如表1所示，经过分析可知：相较于增大立柱间距和立柱直径，通过增大立柱倾角提高稳定性，平台质量及排水体积的增长率最低[18]；随立柱倾角增大，平台稳定性增强，但过大的立柱倾角会引起明显的波浪爬高，同时对立柱和底部浮筒连接处的应力不利。由于缺乏相关的研究，为安全起见，立柱倾角暂定为30°。平台稳性分析结果图2所示，稳性高度为13.00 m，静平衡角为6.72°，面积比1.45，满足DNV规范[19]要求。平台最终参数如表2所示，设计水深为50 m，平台吃水深度为20 m，排水量为14 598 m3。

表1 DTU 10 MW风力机参数[11]Table 1 Main parameters of DTU 10 MW wind turbine[11]

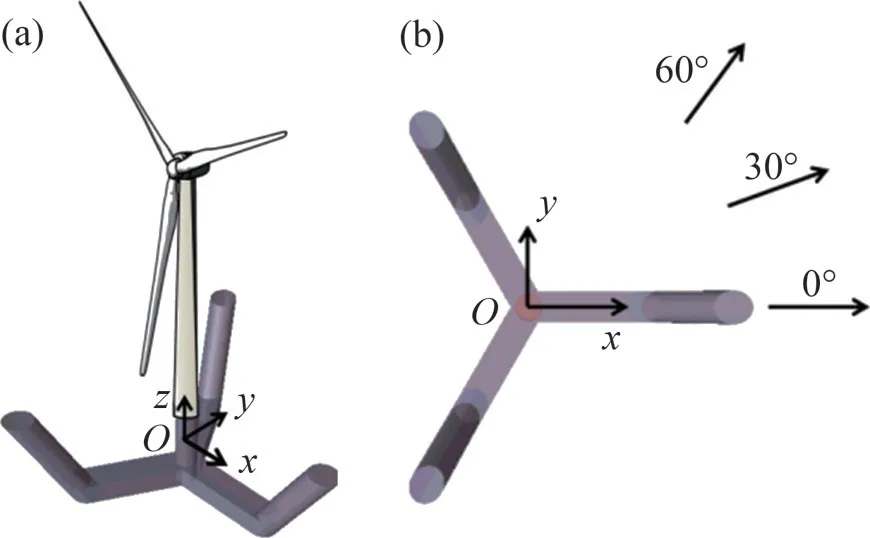
图1 半潜浮式风机概念设计Fig.1 Conceptual design of floating platform

图2 力矩曲线图Fig.2 Heeling and righting moment of floating platform

2 新型半潜浮式风机系泊系统

针对50 m 水深及中国典型海况条件设计了4种不同的悬链式系泊系统，系泊系统如图3所示。图3中：锚链I 为锚链+压载块组合，锚链II 为锚链+浮筒组合，锚链III为含压载块的双锚链，锚链IV 为含浮筒的双锚链；红色方块为压载块，绿色圆圈为浮筒；ML1～6 为系泊线相应的编号。系泊系统导缆孔位于水下15 m 处，与平台中心水平距离42.66 m，其中系泊系统中锚链III 和IV 的夹角为30°。系泊线参数如表3所示，其中锚链材质为无挡锚链，压载块为铅质。

表3 系泊线参数Table 3 Properties for the mooring line

图3 系泊线布置图Fig.3 Mooring line configurations

3 计算理论

漂浮式风机在风、浪、流作用下的时域运动方程可以表示为

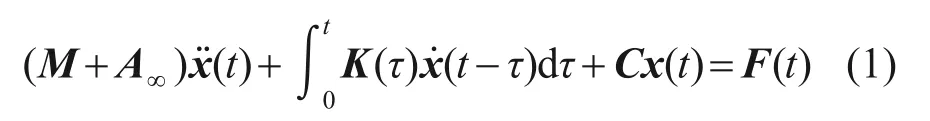
式中：t为时间；x(t)，和分别为平台位移、速度和加速度；M为质量矩阵；C为静水刚度矩阵；A∞为频率无穷大时的附加质量；K(τ)为迟滞函数；τ为迟滞时间。

K(τ)通过势流阻尼得到：

式中：a(ω)通过附加质量矩阵A(ω)减去A∞得到；b(ω)为势流阻尼矩阵B(ω)。

式(1)中F(t)可以表示为环境载荷(风浪等)、系泊系统非线性回复力、风机系统的惯性力以及阻尼力之和：

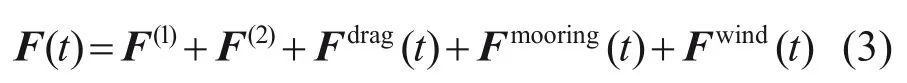
式中：F(1)和F(2)分别为一、二阶波浪激励力，F(1)基于面元法的辐射衍射分析得到，F(2)通过求解自由水面模型的QTF 函数得到，在时域分析中将波浪载荷转换为Simo 中的传递函数；Fdrag(t)为非线性拖曳力，通过莫里森方程计算得到；Fmooring(t)为系泊力，通过集中质量法得到；Fwind(t)为风载荷，采用叶素−动量理论(BEM)计算得到。

4 浮式平台静力分析

在SESAM Sima 中进行不同潮位下的静力分析，得到对应不同潮位的平台吃水深度(表4)和导缆孔处初始张力(图4)，其中，正值代表平台吃水深度增大。由表4可以看出：随潮位变化，悬链段长度的变化对平台吃水深度影响较小，可以忽略不计，而且锚链−浮筒组合系泊系统的吃水变化比锚链−压载块组合系泊系统的吃水变化小。

表4 不同潮位下的平台吃水变化Table 4 Draft change with different tidal levels

由图4可以看出：导缆孔处初始张力随潮位的升高而增大，从平均潮位到高潮位，锚链I的初始张力增加152.5 kN，锚链II 的初始张力增加79.3 kN，锚链−浮筒组合系泊系统的导缆孔初始张力变化比锚链−压载块组合系泊系统的小。此外，从平均潮位到高潮位，锚链III 的初始张力增加133.5 kN，锚链I的初始张力增加59.9 kN，分别比锚链I和锚链II的初始张力增量小。潮位变化对锚链−浮筒组合系泊系统导缆孔张力的影响相对于锚链−压载块组合系泊系统较小，而且增加系泊线数量，平台更适用于大潮差海域。

图4 不同潮位下的导缆孔初始张力Fig.4 Initial tension at fairlead with different tidal levels

5 浮式平台耦合时域分析

5.1 自由衰减

对浮式平台的自由衰减进行分析，模拟时长1 000 s，得到平台在不同潮位下对应的固有周期。图5所示为平均潮位下不同系泊系统对应的纵荡自由衰减时程曲线，图6所示为不同潮位下的平台纵荡周期。由图6可以看出：平台纵荡周期随潮位变化的趋势与导缆孔初始张力随潮位变化的趋势相反。在高潮位，平台抬升导致导缆孔张力增加，系泊线在导缆孔处的竖向夹角变大(以锚链I为例，平均潮位为54.58°，高潮位为55.63°)，从而增大了水平刚度，纵荡周期随之降低；而在低潮位工况下平台下沉，导缆孔处张力和系泊线竖向夹角缩小，水平刚度减小，纵荡周期提高。

图5 平均潮位下的纵荡自由衰减时程曲线Fig.5 Time series curves of free decay in surge direction with mean tidal levels

图6 不同潮位下的平台纵荡周期Fig.6 Surge periods of platform with different tidal levels

从平均潮位到高潮位，锚链I 的纵荡周期由61.21 s 降低至57.68 s，降低了5.77%，锚链II，V和IV的纵荡周期分别降低6.98%，5.44%和5.43%。可以看出，增加系泊线数量会减小潮位变化对平台纵荡周期的影响，尤其对锚链−浮筒组合系泊系统更为显著。

5.2 风浪联合工况

为研究风浪和潮差对新型半潜浮式风机动力响应的影响，模拟半潜浮式风机系统在不同潮位及风浪条件下的运动响应，设计水深为50 m。根据文献[20]和海域资料确定典型风浪和极端潮位，停机工况选用50 a重现期，运行工况选用10 a重现期，波浪要素由波高和周期联合概率密度分布确定，设计工况如表5所示，其中，有义波高指将波高按从大到小的顺序排列，总数前三分之一的平均波高。湍流风采用Kaimal 谱，波浪采用JONSWAP 谱，谱峰升高因子为3.3，风浪同向，均为0°。由于潮位实测数据较少，本文对极端高潮位和极端低潮位在运行和停机工况下均按50 a一遇重现期选取，分别为3.39 m 和−0.42 m。图7所示为不同工况下的风速和波浪时程曲线，模拟时长为4 800 s，去除前1 200 s 以消除瞬态效应，时间步长取0.03 s。

图7 风速和波面时程曲线Fig.7 Time series curves of wind speed and wave elevation

表5 设计工况参数Table 5 Parameters for designed load cases

5.2.1 平台纵荡

图8～10 所示分别为运行工况和停机工况下半潜浮式风机平台在不同潮位的纵荡运动响应时程曲线及统计分析结果。

图8和图10(a)所示分别为运行工况下不同潮位平台的纵荡位移时程曲线和统计值。由图8和图10(a)可知：在运行工况下，除锚链IV 在平均潮位的平台纵荡位移最大值比高潮位的略小以外，平台纵荡位移的最大值、最小值、平均值和标准差都随潮位的降低而增大；此外，在低潮位，锚链I的平台纵荡位移的最大值、平均值和标准差均比锚链II 的大，锚链III 平台纵荡位移的最大值、平均值和标准差均比锚链IV的大。与锚链I相比，锚链III同样采用锚链−压载块组合系泊系统，但系泊线数量由3根增加到6根；与锚链II相比，锚链IV采用锚链−压载块组合系泊系统，但系泊数量也由3 根增加到6 根。以平均潮位为例，锚链I 的纵荡位移平均值为5.45 m，锚链III 的纵荡位移平均值为5.40 m，降低了0.92%，而锚链II 的纵荡位移平均值为5.29 m，锚链IV 的为5.18 m，降低了2.08%。由此可知，采用锚链−浮筒组合系泊系统的平台纵荡运动性能较锚链−压载块组合系泊系统更为优良，增加系泊线数量会显著提高锚链−浮筒组合系泊系统对应的平台纵荡运动性能。

图8 运行工况下不同潮位平台纵荡位移时程曲线Fig.8 Time series curves of surge motion displacement at different tidal levels with operating condition

平台的纵荡位移均值和最大值随潮位的变化而变化。锚链I 在平均潮位的纵荡位移平均值为5.45 m，低潮位的纵荡位移平均值为5.51 m，增加了1.10%，锚链II在平均潮位的纵荡位移平均值为5.29 m，低潮位的纵荡位移平均值为5.36 m，增加了1.32%，锚链III 和锚链IV 的位移平均值分别增加了0.87%和0.89%，可知增加系泊线数量会减小潮位变化对平台纵荡位移均值的影响。锚链I在平均潮位和低潮位的纵荡位移最大值均为9.03 m，由平均潮位到低潮位，锚链II对应的纵荡位移最大值由8.39 m变为8.47 m，增加了0.95%，同样地，锚链III 对应的纵荡位移最大值增加了0.42%，锚链IV的增加了0.61%，可知增加系泊线数量会减小潮位变化对锚链−浮筒组合系泊系统的平台纵荡最大值的影响，增大潮位变化对锚链−压载块组合系泊系统的平台纵荡位移最大值的影响。

图9和图10(b)所示分别为停机工况下不同潮位平台的纵荡位移时程曲线和统计值。由图9和图10(b)可知：在停机工况下，平台纵荡位移的平均值都随潮位降低而增加；平台纵荡位移的标准差随潮位降低而减小，但变化幅度较小；对于平台纵荡位移的最大值，锚链I和锚链III随潮位减低而增大，锚链II 和锚链IV 随潮位降低而减小。可以得出，在3 种潮位下，锚链I 对应的纵荡位移最大值为7.64 m，锚链III 对应的纵荡位移最大值为7.53 m，减小1.44%，同理，锚链II 对应纵荡位移最大值为7.59 m，锚链IV 对应纵荡位移最大值为7.29 m，减小了3.95%。

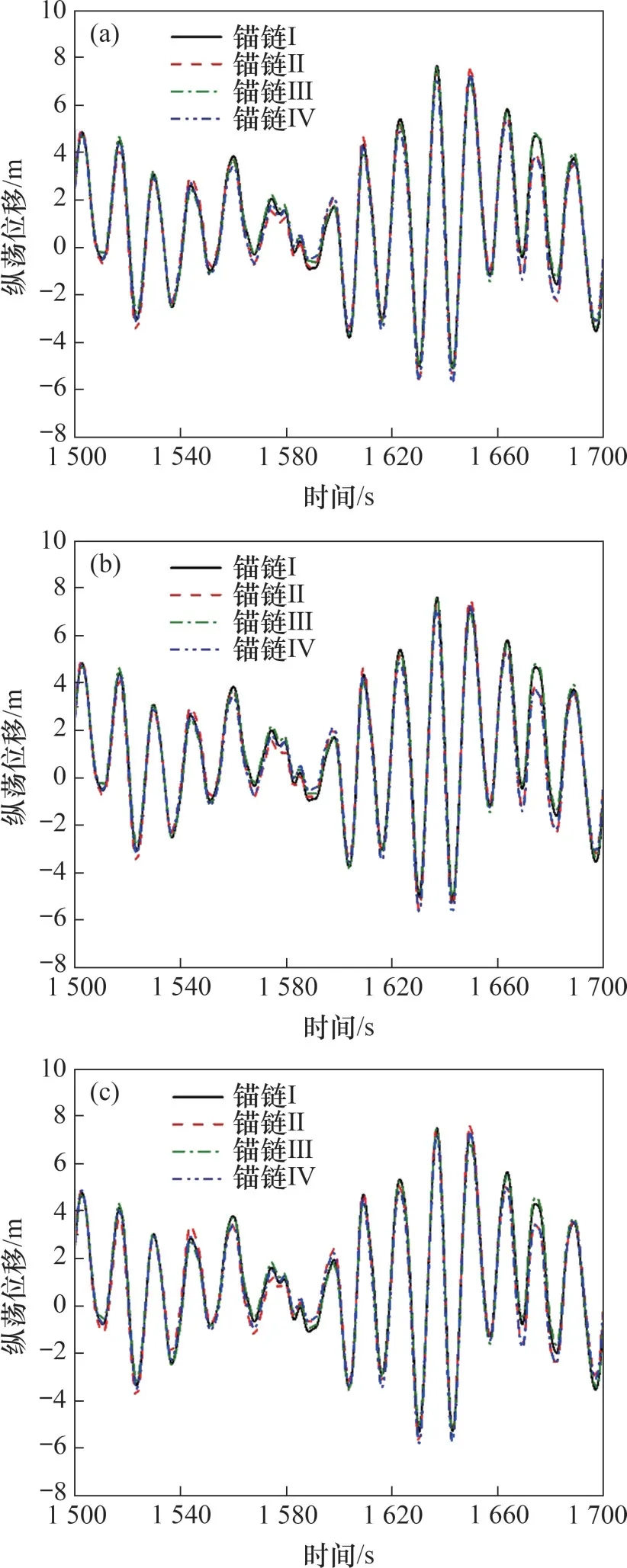
图9 停机工况下不同潮位平台纵荡位移时程曲线Fig.9 Time series curves of surge motion displacement at different tidal levels with parked condition

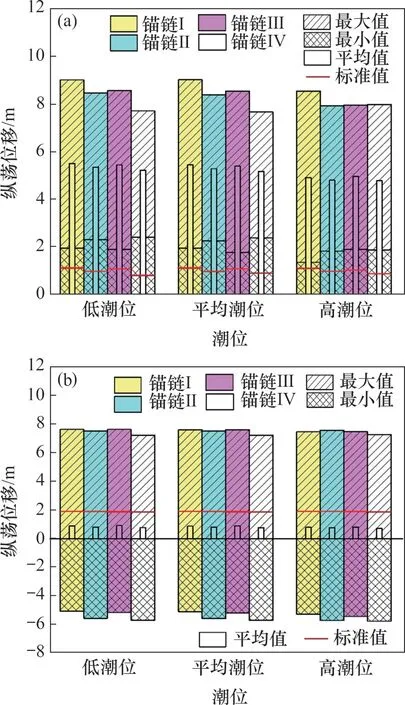
图10 不同工况下平台纵荡位移统计Fig.10 Statistics of surge displacement of platform at different conditions

在停机工况下，锚链I在高潮位的纵荡位移最大值为7.48 m，在平均潮位的纵荡位移最大值为7.62 m，增大了1.87%，锚链II 在高潮位的纵荡位移最大值为7.59 m，平均潮位的纵荡位移最大值为7.54 m，减小了0.66%，同样地，锚链III 增加了2.05%，锚链IV 减小了0.62%，可知在停机工况下，平台纵荡位移的最大值几乎不受潮位的影响，与运行工况一样，增加系泊线数量对锚链−压载块和锚链−浮筒2 种组合系泊系统受潮差条件而变化的趋势影响相反。

综上所述，在停机工况下，波浪载荷对平台运动的影响更为显著，平台纵荡方向基本上在平衡位置随波浪往复运动，相较于运行工况，纵荡运动具有更强的波动性，即停机工况下纵荡运动的标准差比运行工况的标准差大。通过纵荡位移最大值、均值和标准差可以看出，平台纵荡运动在运行工况下受潮位变化的影响显著，其中锚链III受潮位变化的影响最小，但增加系泊线数量后，锚链IV 相较锚链II 受潮位变化的影响明显减弱。在运行和停机工况下，锚链IV 对应平台纵荡的幅值均最小。

5.2.2 锚链张力

图11和图13(a)所示分别为运行工况下不同潮位平台的迎浪侧系泊线张力时程曲线和统计值，图12和图13(b)所示分别为停机工况下不同潮位平台的迎浪侧系泊线张力时程曲线和统计值，锚链I和锚链II 的张力时程对应系泊线ML2，锚链III 和锚链IV 的张力时程对应系泊线ML4。由图11～13可知：在运行工况和停机工况下，锚链张力的最大值、平均值和标准差均随潮位升高而增大。

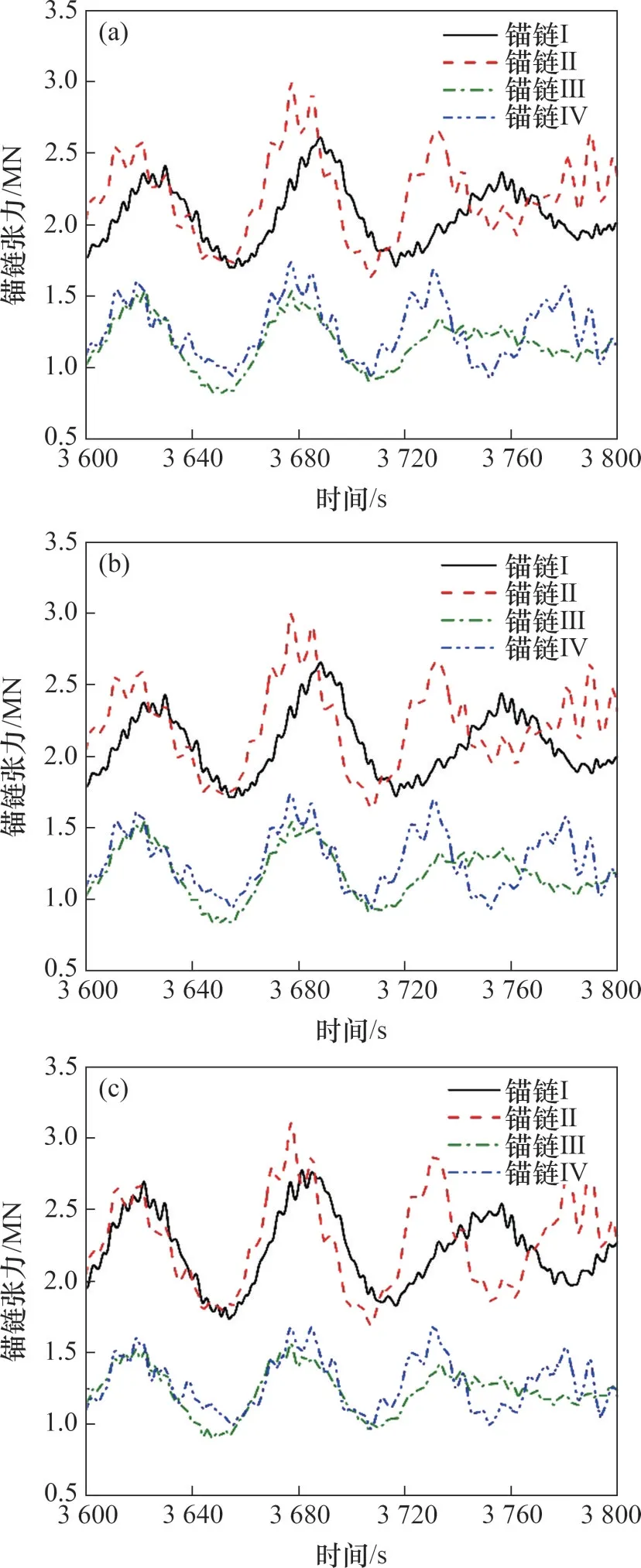
图11 运行工况不同潮位锚链张力时程曲线Fig.11 Time series curves of mooring line tension at different tidal levels with operating condition

图12 停机工况不同潮位锚链张力时程曲线Fig.12 Time series curves of mooring line tension at different tidal levels with parked condition

图13 不同工况下锚链张力统计Fig.13 Statistics of mooring line tension at different conditions

在运行工况下，从低潮位到平均潮位，锚链−浮筒组合系泊系统的锚链张力最大值增长率比锚链−压载块组合系泊系统的增长率小，但从平均潮位到高潮位，锚链−浮筒组合系泊系统的锚链张力最大值增长率远比锚链−压载块组合系泊系统的增长率大，可见，随潮位的升高，锚链−浮筒组合系泊系统的锚链张力最大值的增长率逐渐增大。在停机工况下，锚链−浮筒组合系泊系统的锚链张力最大值增长率较小，始终比锚链−压载块组合系泊系统的增长率小。

综上所述，在不同工况和潮位下，不同系泊系统的锚链张力均值差别较小，停机工况下的锚链张力幅值均比运行工况下的幅值大，且不同系泊系统的锚链张力受潮位变化影响的影响规律在运行和停机工况下有着明显区别，可以看出，在波浪荷载占主导作用的停机工况下，锚链−浮筒组合系泊系统的系泊张力受潮位变化影响较小，但锚链−浮筒组合系泊系统的锚链张力最大值和标准差均比锚链−压载块组合系泊系统大，尤其在停机工况下，锚链−浮筒组合系泊系统的锚链张力最大值比锚链−压载块组合系泊系统大50%左右。