基于轮轨系统耦合振动的地铁钢轨波磨研究
2022-09-21汤雪扬蔡小培彭华马超智
汤雪扬,蔡小培,彭华,马超智
(北京交通大学土木建筑工程学院,北京,100044)
钢轨波磨是地铁线路常见的钢轨损伤形式,我国多条地铁线路在运营过程中出现了钢轨波磨问题,其几何特征呈现周期性波动,使得轮轨接触关系不断恶化,加剧了轮轨间的复杂相互作用,造成轮轨力剧烈增大,严重时甚至导致车辆及轨道零件损坏[1−3]。因此,亟需探明钢轨波磨的形成原因及其影响因素,以便为地铁线路的优化设计和养护维修提供理论指导。
对于钢轨波磨成因的研究,国内外学者已进行了大量的工作。GRASSIE[4]结合既有文献和工程实践经验,将波磨按照其成因分为损伤机理和固定波长机理。波长固定机理认为所有类型的钢轨波磨都与轮轨系统的共振有关,包括轮对的弯曲共振和扭转共振、轨道的垂直共振[5−6],P2共振和Pinned-pinned 共振[7−9]。闫子权等[10]通过建立轮对三维有限元分析模型,分析了轮对垂向及扭转振动,揭示了钢轨波磨与轮对振动之间的关系。李响等[11]通过分析曲线半径300 m的钢弹簧浮置板轨道中钢轨、轨道板垂向弯曲振型以及频谱特性,发现轨道系统的垂向振动可能是导致钢轨波磨产生及发展的主要原因。李霞等[12]建立梯形轨枕轨道模型对梯形轨枕曲线轨道上的波磨进行分析,发现钢轨相对于轨枕的垂横向弯曲振动是诱发钢轨波磨的关键因素。文献[13−14]对“科隆蛋”扣件轨道结构发生的钢轨波磨进行研究,潘兵等[13]认为钢轨波磨的产生与轮轨耦合条件下钢轨的横向弯曲振动有关,而李伟等[14]则认为与轨道结构的垂向弯曲振动特性密切相关。周志军等[15]建立单轮−轨道模型对普通扣件和减振扣件轨道曲线段钢轨波磨进行了分析,发现轮轨耦合的高频模态特征是加剧短波长钢轨波磨的重要原因。既有文献多针对减振轨道或小半径曲线地段,通过单独考虑轮对或轨道的振动,很好地揭示了钢轨波磨的成因。本文所研究的钢轨波磨出现于普通整体道床地段,传统的单独考虑轮对或轨道振动的模型忽视了轮轨之间的耦合关系,对于轮轨系统振动特征的研究不够全面,需寻找更为合理的振动分析模型对钢轨波磨成因进行分析。
本文作者通过对地铁短枕式整体道床出现的钢轨波磨进行现场测试,获得波磨特征,建立可考虑轮对与钢轨相互作用的单轮对−轨道模型以及同时考虑轮轨相互作用和钢轨振动波反射[16−17]的双轮对−轨道模型,并与单独考虑轮对和轨道的模型进行对比,明确适用于钢轨波磨成因分析的理论模型,从轮轨系统耦合振动角度揭示钢轨波磨的形成原因,并进一步分析转向架轴距与扣件刚度对钢轨波磨波长及幅值的影响。
1 现场波磨状态测试
为准确测量钢轨表面的波磨情况,利用连续测量的高精度波磨小车对某地铁曲线段短枕式整体道床轨道的波磨状态进行现场测试,测试段长度为180 m,曲线半径为800 m,现场波磨情况如图1所示。
图2所示为该地段一侧钢轨表面不平顺随里程的变化关系。从图2可以看出:该地段钢轨不平顺峰值水平在50 μm左右,个别里程处钢轨表面不平顺幅值达到150 μm。

图2 钢轨不平顺Fig.2 Rail irregularity
为评价该地段波磨波深幅值特征,本文采用BS EN 13231—3:2006[18]中规定的移动波深幅值峰峰平均值(PPV)以及固定测量长度内的超限比例作为钢轨表面不平顺的评价指标。该规范将波磨波长范围分成4 个部分,分别为10~30 mm,30~100 mm,100~300 mm 和300~1 000 mm,并且规定分析窗长及容许限值,如表1所示。由图1可以看出该地段波磨波长较短,因此,本文采用的分析窗长为500 mm,PPV 容许值为10 μm,容许超限率为5%。图3所示为移动波深幅值峰峰平均值随里程的变化关系。从图3可以看出:实测PPV在绝大部分里程处超出容许值,超限率为98%,远远高于容许超限率5%,说明该地段钢轨波磨情况十分严重。
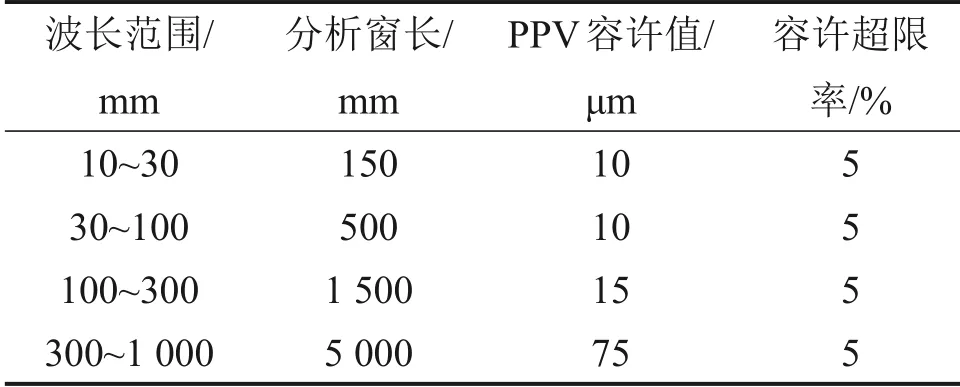
表1 欧洲铁路联盟BS EN 13231-3:2006 评价标准Table 1 European RAILWAY Union BS EN 13231-3:2006 evaluation standard

图3 移动波深幅值峰峰平均值Fig.3 Peak-to-peak average moving wave depth amplitude
为了更加清晰地描述钢轨波磨波长特征,根据BS EN ISO 3095:2013[19]中规定的计算方法,对所测钢轨表面粗糙度进行1/3倍频程波长谱分析并与规范中的规定数值进行对比,如图4所示。由图4可以看出:该地段钢轨粗糙度在多个波长范围内严重超出ISO 3095 标准中规定的钢轨表面粗糙度限值,其主波长为50 mm,超出限值20 dB 以上,次波长为315 mm,超出限值5 dB以上。
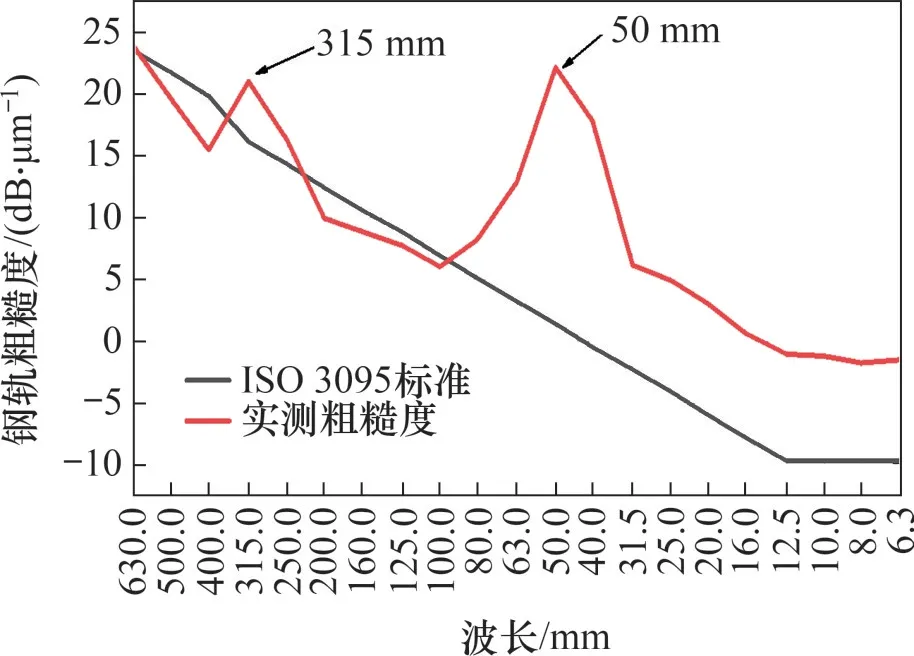
图4 钢轨粗糙度Fig.4 Roughness of rail
由于该地段位于线路区间中部位置,行车速度较快,约为85 km/h,钢轨主波长(50 mm)和次波长(315 mm)对应的波磨通过频率f1和f2分别为:

2 有限元模型
为准确揭示钢轨波磨与轮轨系统振动特征之间的内在联系,本文建立轮对模型、轨道模型、单轮对−轨道模型(可考虑轮轨相互作用)以及双轮对−轨道模型(可同时考虑轮轨相互作用和钢轨振动波的反射),通过提取各模型特征频率并与波磨通过频率对比,明确适用于钢轨波磨成因分析的模型。
2.1 轮对模型
根据表2所示的参数建立地铁B型车拖车轮对有限元模型,如图5所示。轮轴两侧通过弹簧阻尼单元模拟一系悬挂系统,并与固定边界连接,不考虑轮对与钢轨的相互作用。

图5 轮对模型Fig.5 Wheelset model
2.2 轨道模型
当激励作用于轨道上时,该激励的影响范围是有限的,为了保证仿真计算的精度并且节约计算时间,选取20 跨扣件间距的轨道模型进行仿真分析,基于有限元软件ABAQUS,建立短枕式整体道床轨道模型,如图6所示。短枕式整体道床轨道结构主要由钢轨、扣件和轨道板组成。模型中钢轨类型为60 kg/m,扣件为DTVI2型扣件,轨道板为C40 混凝土,扣件间距为0.625 m,钢轨、轨道板均采用C3D8R 单元模拟。利用Python 脚本语言对ABAQUS 进行二次开发,批量生成wire 并赋予其弹簧和阻尼器属性,模拟扣件系统以及道床与地基之间的连接,为更真实地模拟扣件对钢轨的约束作用,在扣件连接位置对轨道板进行网格加密,避免了传统采用单一弹簧阻尼器模拟扣件导致扣件连接位置出现局部应力集中的情况,钢轨和轨道板两端均采用对称约束,模型参数如表2所示。
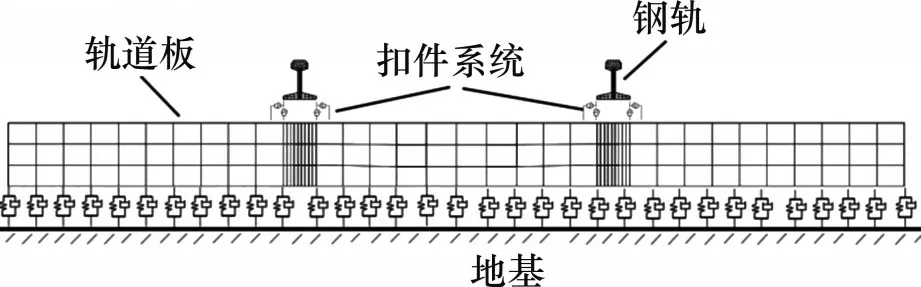
图6 轨道模型Fig.6 Track model
2.3 轮轨耦合模型
单轮对−轨道模型如图7所示,双轮对−轨道模型如图8所示。将轮轨间的垂向接触视为2个弹性体的赫兹接触问题,由于模态分析忽略系统间的非线性特征,将轮轨接触非线性弹簧刚度进行线性化处理,采用若干个线性弹簧模拟轮对与钢轨间的相互作用,模型参数如表2所示。

图7 单轮对−轨道模型Fig.7 Single wheelset−track model

图8 双轮对−轨道模型Fig.8 Double wheelset−track model

表2 仿真模型参数Table 2 Parameters of simulation model
根据赫兹接触理论,轮轨间因弹性变形而产生的压缩量为

式中:δ为轮轨相对压缩量;P为轮轨间的垂向作用力;ρ为由车轮踏面和轨头2 个垂直方向的半径计算得到的常数;K为与车轮及钢轨材料的弹性模量和泊松比有关的常数;λ为椭圆积分常数,依据车轮踏面和轨头2 个垂直方向的半径计算并查表得到。
由式(3)可得

本文中车轮踏面为磨耗型踏面,
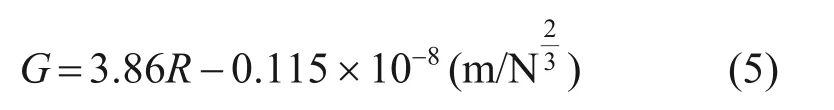
式中:R为车轮半径,m。
根据垂向力与轮轨间弹性压缩量的关系,可以得到轮轨非线性弹簧接触刚度为
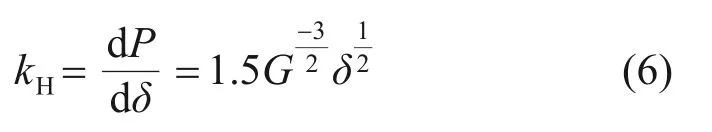
接触弹簧线性化时,将静轮载P0代入式(3)得到静压缩量δ0,再代入式(6)即可得到线性化接触弹簧刚度。本文取轮轨线性化接触刚度为1.524×109N/m[20]。
3 模型振动特征与波磨成因关系分析
3.1 轮对模型振动特征
为研究轮对振动特征与钢轨波磨的关系,本节对轮对模型进行模态分析。图9所示为波磨通过频率附近的轮对模态振型,轮对在477.04 Hz 和477.19 Hz处分别发生纵向和垂向的二阶弯曲振动,该固有频率与主波长为50 mm 的钢轨波磨通过频率相近,说明主波长50 mm 波磨的产生与轮对在477 Hz 附近处的纵向和垂向二阶弯曲振动有关。值得注意的是,在轮对固有频率中并未发现与次波长315 mm波磨通过频率相近的频率成分,因此仅采用轮对模型无法全面分析该地段钢轨波磨的形成原因。
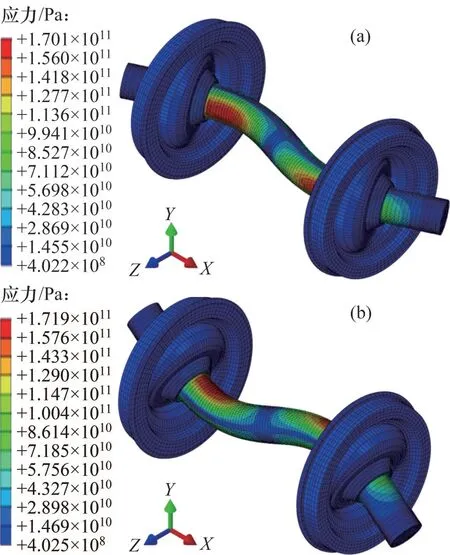
图9 轮对模态振型Fig.9 Modal vibration mode of wheelset
3.2 轨道模型振动特征
对轨道模型施加1~1 500 Hz 单位简谐激振力进行谐响应分析,钢轨跨中以及轨枕上方的钢轨位移频响函数如图10所示。从图10可以看出:轨道模型的垂向Pinned-Pinned 共振频率在1 200 Hz左右,Pinned-Pinned 共振的半个共振波长为一个扣件间距,该共振模态下钢轨在跨中的振动幅度最大,而在轨枕上方的振动幅度几乎为零,Pinned-Pinned 共振频率主要由钢轨类型和轨枕间距决定[21]。由文献[13]可知,扣件间距为0.625 m,钢轨类型为60 kg/m 的轨道结构垂向Pinned-Pinned共振频率为1 151 Hz,与仿真计算的垂向Pinned-Pinned共振频率基本一致,验证了本文模型的正确性。轨道模型固有频率中并未发现与主、次波长波磨通过频率相接近的频率,说明仅采用轨道模型仍无法对该地段钢轨波磨的成因作出解释。
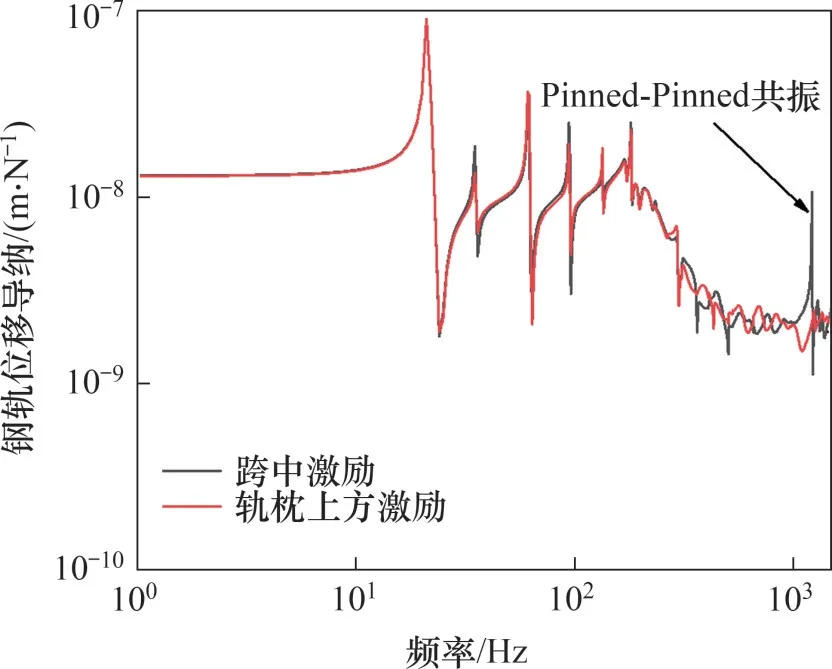
图10 轨道模型钢轨位移导纳Fig.10 Rail displacement admittance of track model
3.3 轮轨耦合模型振动特征
对单轮对−轨道模型和双轮对−轨道模型施加1~1 500 Hz单位简谐激振力进行谐响应分析,并结合轮轨系统模态振型,揭示波磨通过频率附近的轮轨振动特征,明确钢轨波磨的产生原因。
图11所示为单轮对−轨道模型和双轮对−轨道模型钢轨跨中以及轨枕上方的钢轨垂向位移导纳。从图11可以看出:2 个模型的Pinned-Pinned 共振频率均在1 200 Hz左右,验证了模型的正确性。此外,结合轨道模型的Pinned-Pinned 共振频率可以发现,由于轮对数量增加,钢轨受到的约束作用增强,抑制了钢轨垂向Pinned-Pinned 共振,使得跨中激励所激发的共振幅值有所降低。
表3所示为单轮对−轨道模型和双轮对−轨道模型在钢轨波磨通过频率处的模态振型及其对应频率。图12和图13所示分别为单轮对−轨道模型和双轮对−轨道模型在钢轨波磨通过频率处的模态振型云图。从图12和图13可以看出:在次波长波磨通过频率75 Hz附近,轮对与轨道参振质量相对于弹性基础发生共振(P2 共振),轮对−轨道模型的共振影响范围约为3 个扣件间距,双轮对−轨道模型的共振影响范围更大,约为7个扣件间距。轮轨系统P2共振频率与次波长315 mm对应的波磨通过频率基本一致,说明次波长波磨的产生与P2 共振有关。

表3 模型振型及固有频率Table 3 Vibration mode and natural frequency of model
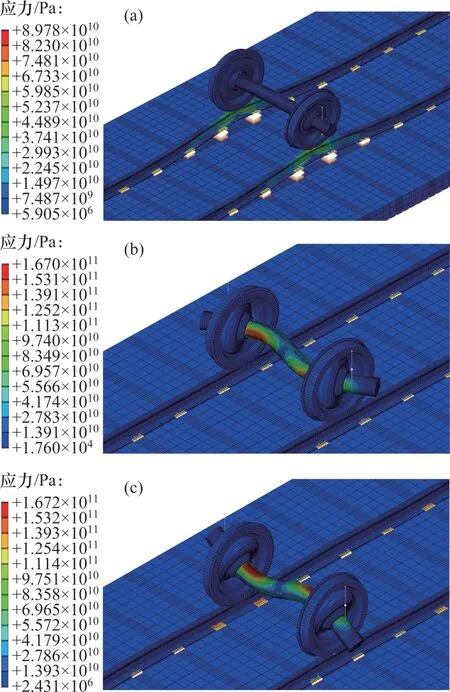
图12 单轮对−轨道模型振型云图Fig.12 Vibration mode cloud chart of single wheelset−track model

图13 双轮对−轨道模型振型云图Fig.13 Vibration mode cloud chart of double wheelsets−track model
在主波长波磨通过频率472 Hz附近,单轮对−轨道模型和双轮对−轨道模型中轮轴均发生纵向以及垂向的二阶弯曲共振(由于两轮对在振动中存在相位差,对于每个自由度的弯曲共振,双轮对−轨道模型存在2 种振型),对比轮对模型在477.04 Hz和477.19 Hz 处的纵向和垂向二阶弯曲振动可以发现,轮轨耦合模型的振动频率较轮对模型更低,且更接近主波长波磨通过频率472 Hz,这是由于轮轨耦合模型考虑了钢轨与轮对之间的相互作用,使得轮对振动更接近实际情况。
轮轴的纵向振动导致车轮与钢轨接触面之间发生纵向滑动,纵向蠕滑率增大,导致纵向蠕滑力增大;轮对的垂向振动则导致轮轨垂向接触力以相同频率周期性波动,在接触斑最大应力超过钢轨材料屈服应力的区域,钢轨表面发生磨损,长期运营条件下则会导致钢轨波磨的产生。值得注意的是,在主波长通过频率附近,双轮对−轨道模型中还存在轮对间钢轨的横向三阶弯曲振动,其频率与转向架轴距有关[22]。通过以上分析可以发现,主波长波磨的产生与轮轴的纵向、垂向二阶弯曲振动以及轮对之间钢轨的横向三阶弯曲振动有关。
通过对比钢轨波磨通过频率与轮对模型、轨道模型、单轮对−轨道模型以及双轮对−轨道模型的固有频率可知,单独考虑轮对或轨道模型无法揭示该地段钢轨波磨的形成原因,单轮对−轨道模型和双轮对−轨道模型在分析钢轨波磨成因时较为全面,但单轮对−轨道模型忽视了两轮对间钢轨振动波的反射,无法给出钢轨振动波在轮对间反射时的轮轨系统振动特征,对钢轨波磨成因的分析仍存在一定的局限性;双轮对−轨道模型同时考虑了轮轨相互作用以及钢轨振动波在轮对间的反射,对于波磨通过频率处的轮轨系统振动特征描述更为全面。因此,建议采用双轮对−轨道模型对钢轨波磨成因进行分析。
4 钢轨波磨影响因素分析
4.1 波磨波长影响因素
本节基于双轮对−轨道模型,研究不同转向架轴距(1.8,2.0,2.2,2.4 和2.6 m)及扣件刚度(24,32,40,48 和56 kN/mm)下的轮轨系统振动特征,并进一步分析转向架轴距及扣件刚度对波磨波长的影响。
图14所示为不同转向架轴距、扣件刚度下的轮轨系统振动频率变化曲线。从图14可以看出:随着转向架轴距增大,P2 共振频率以及轮轴纵、垂向振动频率基本不发生变化,轮对间钢轨的横向弯曲振动频率明显减小,这是由于轮对间的弯曲振型波长与轴距有关,轴距的增加使得弯曲波长变大,弯曲振型的频率降低;随着扣件刚度的增大,P2 共振频率显著增大,其他频率基本变化不大。

图14 轮轨振动特征频率Fig.14 Characteristic frequency of wheel-rail vibration
图15所示为不同转向架轴距、扣件刚度下的轮轨系统振动导致的波磨波长变化曲线。从图15可以看出:随着转向架轴距增大,由钢轨横向弯曲振动导致的波磨波长明显变大,而其他振型导致的波磨波长变化不大;随着扣件刚度增大,由P2 共振导致的波磨波长明显变小,而其他振型导致的波磨波长变化不大。
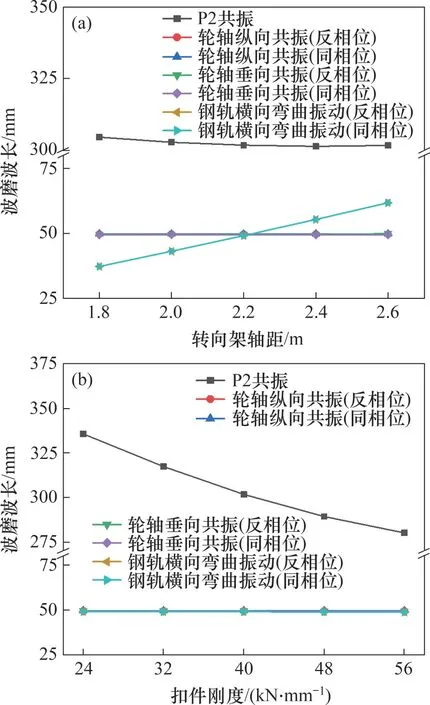
图15 钢轨波磨波长Fig.15 Wavelength of rail corrugation
4.2 波磨幅值影响因素
本节基于双轮对−轨道模型,研究不同转向架轴距(1.8,2.0,2.2,2.4 和2.6 m)及扣件刚度(24,32,40,48和56 kN/mm)下的轮轨接触作用力,并进一步基于Archard磨耗理论分析转向架轴距及扣件刚度对波磨幅值的影响。
当车轮与钢轨发生滚动接触时,车轮踏面和钢轨表面的不平顺会引起动态轮轨力,由于振动波在钢轨中的传播速度远远大于车轮的滚动速度,可以认为车轮在空间中的位置保持不变,钢轨不平顺在轮轨接触面之间以车轮的滚动速度移动,产生轮轨系统的相对位移激励。本文选取波磨的初始波长λ=50 mm,幅值A=0.1 mm,车轮的滚动速度v=85 km/h,时间为t时的不平顺激励可表示为
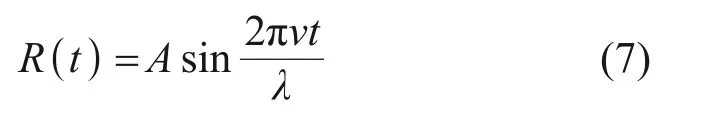
图16所示为轮对与轨道相互作用示意图。从图16可知:在轮对1和轮对2与钢轨的接触位置分别施加相对位移激励R(t),由于轮轨线性化接触刚度的存在,会使轮对1与钢轨之间产生主动轮轨作用力F11以及附加轮轨作用力F12,其中F12包括轮对2处位移激励引起的轮对1处的轮轨作用力P12和轮对2 反射波在轮对1 处引起轮轨作用力Q12。本文建立的双轮对−轨道模型是频域线性模型,满足叠加原理[23],于是轮对1与钢轨的总接触作用力F1为主动轮轨作用力F11、轮轨作用力P12和轮轨作用力Q12三者之和。
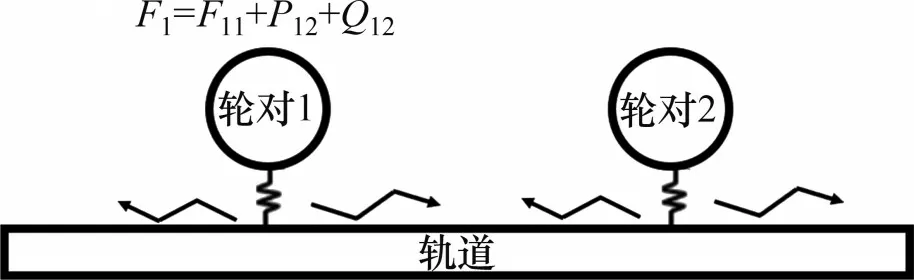
图16 轮轨相互作用示意图Fig.16 Schematic diagram of wheel-rail interaction
Archard 磨耗理论[24]认为,材料磨耗的体积V与接触法向力、滑动距离成正比,与材料的硬度成反比,即

式中:k为磨耗系数,可通过大量磨耗实验获得;N为接触法向压力;S为相对滑动距离;H为材料的硬度,取摩擦副的较小值。
在相同的轮轨蠕滑状态下,钢轨磨耗与轮轨法向接触力F1呈正相关,且由于主动轮轨作用力只与相对位移激励和接触刚度有关,不同转向架轴距和扣件刚度下主动轮轨作用力导致的轮轨磨耗相同,因此,附加作用力F12对波磨幅值存在显著影响。
图17所示为不同转向架轴距下附加轮轨力时频曲线以及峰值分布情况。从时域图可以看出:不同轴距下的附加轮轨力波动范围不同,轴距为2.0 m时波动幅值最小,轴距为2.4 m时波动最为剧烈;从频域图可以看出:不同轴距下的附加轮轨力峰值均出现在70 Hz 和472 Hz 处,70 Hz 处的峰值可能与轮轨系统的低阶固有频率有关,472 Hz处的峰值则与相对位移激励的频率有关;从峰值分布图可以看出:随着转向架轴距增加,附加轮轨力先减小后增大而后又减小,呈现波动趋势,这可能是由于不同轴距下轮对2处激励在轮对1处产生的轮轨力P12与轮对2反射波在轮对1处引起轮轨作用力Q12相位差不同,导致叠加后的附加轮轨作用力F12呈现波动趋势,轮轨力峰值的最小和最大值分别出现在轴距2.0 m和2.4 m处。
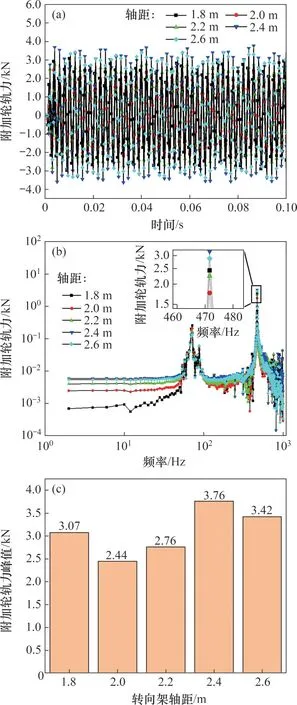
图17 不同转向架轴距下的附加轮轨力Fig.17 Additional wheel-rail forces at different vehicle axle distances
附加轮轨作用力F12随轴距的变化呈现波动趋势,由于钢轨磨耗增加量与附加轮轨作用力F12成正比,因此,波磨幅值随轴距的变化也同样呈现波动趋势,在轴距2.0 m时波磨幅值最小,在轴距2.4 m时波磨幅值最大。
图18所示为不同扣件刚度下附加轮轨力时频曲线以及峰值分布情况。从时域图可以看出:不同扣件刚度下的附加轮轨力波动范围不同,扣件刚度为24 kN/mm 时波动最为剧烈,扣件刚度为56 kN/mm 时波动幅值最小;从频域图可以看出:不同扣件刚度下的附加轮轨力峰值均出现在70 Hz和472 Hz处,70 Hz处的峰值可能与轮轨系统的低阶固有频率有关,472 Hz 处的峰值则与相对位移激励的频率保持一致;从峰值分布图可以看出:附加轮轨力峰值随着扣件刚度增加而减小,这是由于扣件刚度的增加使得轨道系统的整体性增强,位移激励产生的能量更易向下扩散,从而减弱了轮轨之间的振动,附加轮轨力峰值在扣件刚度为24 kN/mm 时最大,在扣件刚度为56 kN/mm 时最小。
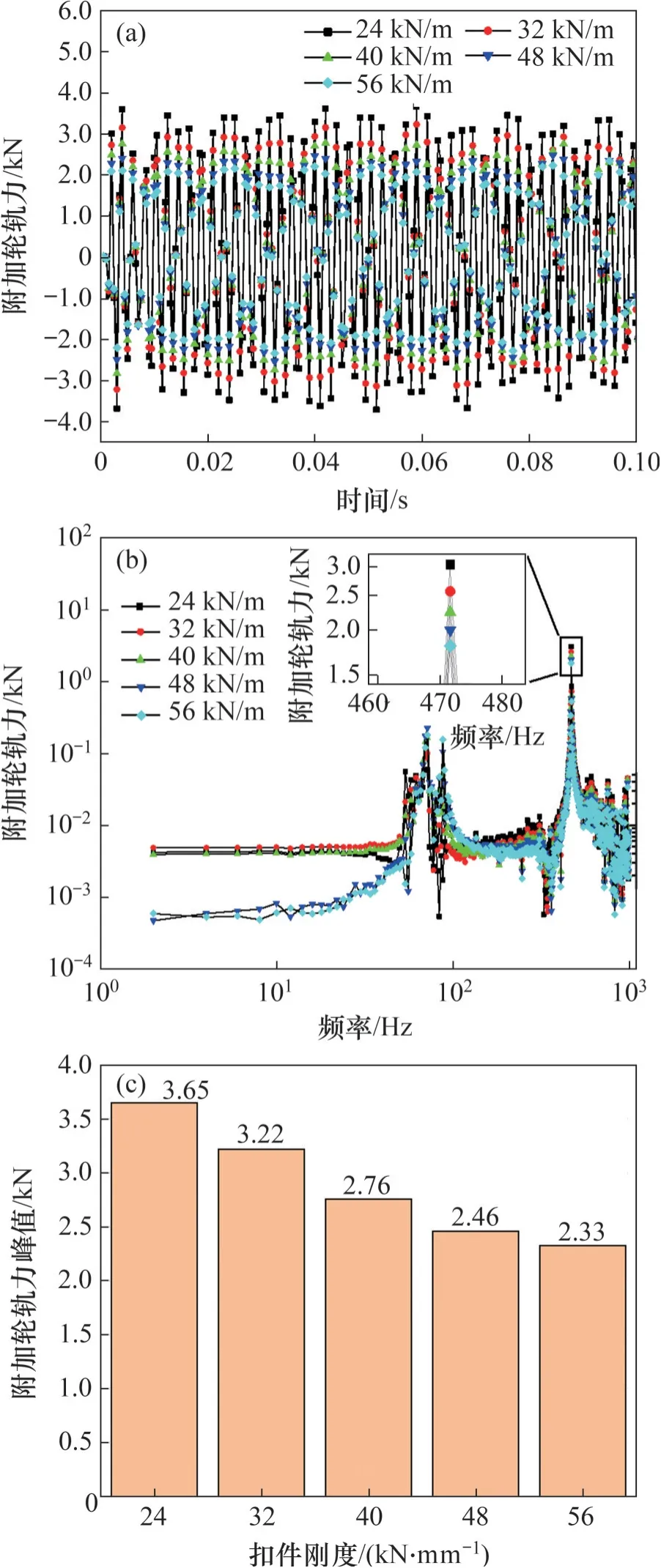
图18 不同扣件刚度下的附加轮轨力Fig.18 Additional wheel-rail forces at different fastener stiffnesses
由于钢轨磨耗增加量与附加轮轨作用力F12成正比,附加轮轨作用力F12随扣件刚度增加而减小,因此,波磨幅值随扣件刚度增加而减小,这一结论也解释了地铁钢轨波磨多发生于减振扣件类轨道的原因[25]。
5 结论
1)该轨道结构钢轨波磨移动波深幅值峰峰平均值超限率为98%,主波长为50 mm,次波长为315 mm,列车的行车速度在85 km/h,主波长和次波长通过频率分别为472 Hz和75 Hz。
2)相比于轮对模型、轨道模型、单轮对−轨道模型,双轮对−轨道模型同时考虑了轮轨相互作用以及轮对间钢轨振动波的反射,能够较为全面地体现轮轨系统振动特征,建议采用双轮对−轨道模型对钢轨波磨成因进行分析。
3)主波长波磨的产生与轮轴的纵向、垂向二阶弯曲振动以及轮对之间钢轨的横向三阶弯曲振动有关;次波长波磨的产生主要与P2共振有关。
4)转向架轴距的增大仅会导致由钢轨横向弯曲振动引起的波磨波长增大,扣件刚度的增大仅会导致由P2 共振引起的波磨波长减小;波磨幅值随轴距增大呈现波动趋势,但随扣件刚度增大而减小。
