盾构隧道曲线段掘进引发邻近地下管线变形分析

2022-09-21邓皇适傅鹤林史越赵运亚黄齐兵

中南大学学报（自然科学版） 2022年8期

邓皇适，傅鹤林，史越，赵运亚，黄齐兵

(中南大学土木工程学院，湖南长沙，410075)

城市地下管道错综复杂，且管道刚度一般较小，周边环境的扰动容易引起管道变形或裂损，影响管线正常使用。城市中盾构隧道掘进会引起周边土体产生极大的附加应力和变形，威胁管线安全[1−3]。张冬梅等[4]基于Kerr 地基梁理论，将已建隧道分别简化为欧拉伯努利梁和铁木辛柯梁，建立了新建隧道施工对上方已建隧道变形计算的解析方法；卢岱岳等[5]推导了新建隧道正面附加荷载、侧壁摩擦力及盾尾土体损失引起的土体位移场，借助Pasternak 地基梁模型确定作用在既有隧道上的附加荷载，最终确定新建隧道引发既有隧道的变形情况；马少坤等[6]开展离心实验并结合数值模拟技术，分析了不同埋深双隧道对邻近地埋管线的影响；林存刚等[7]将管道视为防止Pasternak地基上的连续梁模型，采用有限差分方法推导了盾构隧道开挖地层损失引起地下管线的挠曲曲线公式；可文海等[8]利用Vlasov 迭代流程确定了Pasternak 地基梁模型中的弹性系数k与剪切系数Gc，最后分析了隧道开挖对管道的影响；史江伟等[9]考虑了管线的非连续性，预测了盾构下穿管线时的管线的变形情况。上述研究主要针对盾构机在直线段掘进时的情况，鲜有研究针对盾构机在曲线段掘进时对周边管线的扰动情况，盾构机在曲线段掘进造成的扰动比在直线段掘进时造成的扰动更大。随着城市化进程的不断加快，地铁线路敷设情况越来越复杂，明确盾构机在曲线段掘进时对邻近地下管线变形扰动情况愈发重要。

理论解析方法相比数值模拟方法或室内实验方法，其预测计算效率更高，能在初期设计中，为设计人员提供相应参考，因此，提出盾构隧道曲线段掘进引发地下管线变形的理论预测公式具有较大意义[10−11]。本文作者基于镜像汇源法和Mindlin解，考虑盾构机在曲线段掘进时地层损失、掌子面推力以及盾壳摩阻力非均匀分布的特性，将管线简化为放置在Pasternak 地基梁上的Euler-Bernoulli梁，推导盾构机在曲线段掘进时引发既有管线的变形计算公式，根据实际案例，构建对应的有限差分模型，对比实际监测结果和数值模拟计算结果验证理论计算公式的正确性，最后分析隧道转弯半径R0、隧道半径R以及管道刚度EI对管线变形的影响。

1 地层损失引发变形计算

1.1 盾构机曲线段掘进地层损失模型

盾构机沿曲线段掘进时，在土层强度较高的区域，通常会超挖曲线内侧部分土体以减小土体对盾壳的挤压作用，因此，盾构机在曲线段掘进时的地层损失模型相比直线段更复杂，对周边环境的扰动效应更大。邓皇适等[12]提出了盾构机在曲线段掘进时的地层损失模型，其地层损失由2部分组成：第1 部分地层损失位于盾壳整个范围内，曲线内侧超挖间隙构成了此部分地层损失，如图1中1-1′截面所示；第2 部分地层损失位于盾尾处，盾壳与管片脱空产生的盾尾间隙构成了此部分地层损失，如图1中2-2′截面所示。

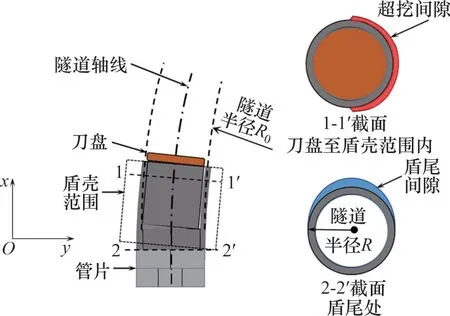
图1 曲线段地层损失模型Fig.1 Ground loss model of curve section

1.2 理论计算依据

镜像汇源法由SAGASETA[13]提出，用于求解半无限体内产生单位体积间隙引起周边位移场分布，计算模型如图2所示。

图2 镜像汇源法计算模型Fig.2 Calculation model of mirror image method

计算点沉降由体积变化引起的沉降分量Sz1，Sz2以及地表切应力引起的沉降分量Sz3叠加而成，3个沉降分量的计算公式分别为

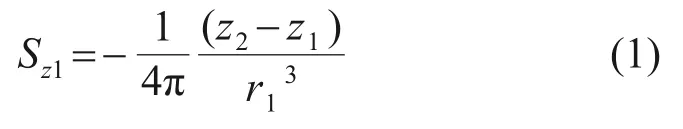
式中：(x2，y2，z2)为计算点坐标；(x1，y1，z1)为空隙点坐标；b和c分别为y方向和x方向的积分上限；u和t为虚拟积分变量；μ为土体泊松比；Rs=[(x2−u)2+(y2−t)2+(z2−z1)2]1/2；r1=[(x2−x1)2+(y2−y1)2+(z2−z1)2]1/2；r2=[(x2−x1)2+(y2−y1)2+(z2+z1)2]1/2。

式(3)可以通过Cerruti 方程确定其积分解[14]，将式(1)，(2)和(3)叠加即可得到半无限体内产生单位空隙引起任意一点的沉降变化总量Sz。

1.3 地层损失引发变形计算公式

计算第1部分地层损失引发的地表沉降时，超挖部分地层损失可以视为2个半圆柱体相减，如图3所示。

图3 超挖部分积分示意图Fig.3 Schematic diagram of over-excavation partial points

图3中，β为超挖刀伸缩角[12]，一般为5°～20°；δ为转弯时所需最小超挖量，计算公式[12]为

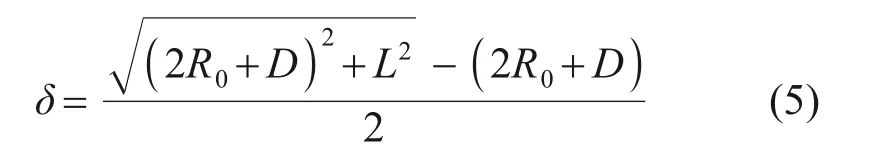
式中：R0为转弯半径，m；D为盾构机刀盘直径，m；L为盾壳长度，m。

根据SAGASETA[13]提出的公式，刀盘至盾尾范围内单位空隙点的坐标(x1，y1，z1)中，各分量为

式中：s为积分点到刀盘的距离，m；θ为积分点与水平线的夹角，(°)；r为积分点到盾壳中轴线的距离，m；H为刀盘中心点埋深，m。

将变换后的坐标代入式(4)，分别对2个半圆柱体积分并相减，得出第1部分地层损失引发周边点位沉降的计算公式为

式(7)采用常规积分方法难以求解，本文根据插值的方法，构建三阶九点Gauss-Legendre插值计算程序进行计算。

LOGANATHAN 等[15]提出了地层损失非均匀分布引发周边土体沉降的计算公式，被广泛用于计算隧道非均匀收敛引发的周边位移场变化情况。本文采用此公式计算第2部分地层损失引发的地表沉降情况，但该公式未考虑此部分地层损失位于盾尾处，需要对公式坐标进行变换，变换后的公式为

式中：(x0，y0，H)为刀盘中心点坐标；(x，y，z)为计算坐标；g为地层损失参数，m；R为隧道半径，m。

将式(7)和式(8)叠加，得到盾构机在曲线段掘进时地层损失引发的周边土体变形计算公式为

2 施工因素引发变形计算

2.1 计算理论依据

MINDLIN[16]以弹性半无限空间体为研究区域，推导了确定点位(x0，y0，z0)在水平荷载Ph和竖向荷载Pv作用下引发空间内任意一点(x，y，z)沉降w1和w2的计算公式，计算模型如图4所示。

图4 Mindlin解计算模型Fig.4 Mindlin solution calculation model

MINDLIN[16]提出的计算公式为

式中：G为土体的剪切模量，MPa；R1=[(x−x0)2+(y−y0)2+(z−z0)2]1/2；R2=[(x−x0)2+(y−y0)2+(z+z0)2]1/2。

MINDLIN[16]提出的计算模型简单明了，公式计算所需参数较少，被广泛用于分析隧道开挖对周边环境的扰动情况[8−12]。为了简化后续计算公式的表达，下面将式(10)和(11)分别简化为：w1=F(Ph，x0，y0，z0，x，y，z)，w2=G(Pv，x0，y0，z0，x，y，z)。

盾构隧道掘进扰动周边的主要施工因素为附加推力、盾壳摩阻力以及注浆压力，施工因素的分布情况见图5。

图5 计算力分布情况Fig.5 Calculation force distribution

2.2 附加推力引发变形计算

在曲线段掘进时，刀盘面上的推力在曲线内外两侧非均匀分布[17]。假定在转弯过程中，推力关于刀盘中心线非对称分布且不考虑刀盘尺寸的影响，弯道外侧附加推力p1与弯道内侧附加推力p2的比值为n(n>1)，即p1=np2。附加推力可以视为一水平荷载，弯道内侧刀盘上任意微元体面积等于dA=rdrdθ，荷载为dPh=p2dA，微元体的坐标需变换为弯道外侧点位只需将y0转换为−y0即可，将变换后的坐标代入式(10)，并对整个刀盘范围进行积分，得到附加推力引发周边点位沉降的计算公式为

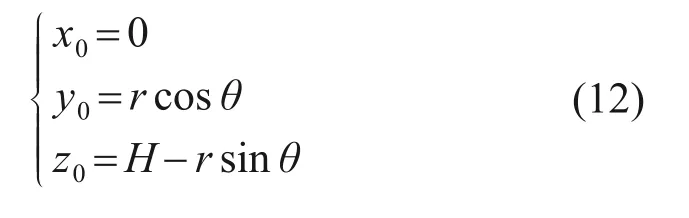
2.3 盾壳摩阻力引发变形计算

盾壳摩阻力与周边土层压力、盾壳与土体的摩擦因数以及开挖导致土体的软化系数有关。张润峰等[18]得出盾壳摩阻力的计算公式为

式中：βs为盾壳周边土体软化系数；σ为作用在盾壳上的法向应力，σ=σvsin2φ+σhcos2φ；σv为竖向土压力，σv=γH−γRsinθ；σh为水平土压力，σh=Kσv，K=1−sinφ；φ为土体内摩擦角，(°)；α为盾壳与土体接触面摩擦角，可参考文献[18]取值。

虽然超挖了曲线内侧部分土体，但盾壳内侧摩阻力仍大于外侧摩阻力[17]，因此，假定弯道内侧盾壳摩阻力f1和弯道外侧盾壳摩阻力f2的比值为m(m>1)，即f1=mf2。盾壳摩阻力可以视为作用在盾壳面上的水平荷载，弯道内侧微元体面积dA=Rdsdθ，荷载dPh=f1dA，微元体的坐标需变换为

将变换后的公式代入式(10)，分别对盾壳内外两侧积分，则盾壳摩阻力引发变形的计算公式为

式中：s为积分点与刀盘间的距离，m；0≤s≤L。

2.4 附加注浆压力引发变形

附加注浆压力q等于盾尾处注浆压力减去水土压力。在实际工程中，注浆压力通常呈鸭蛋式非均匀分布，且影响范围较广[19]，但已有研究表明附加注浆压力对周边土层的扰动较小，通常将其视为分布在盾尾后方单环管片范围内沿面法向的均布荷载[20−21]。

附加注浆压力可以分解为竖向荷载q1和水平荷载q2，其中竖向荷载q1=qsinθ，水平荷载q2=qcosθ，计算范围内微元体面积dA=Rdadθ，微元面积的坐标为

将竖向荷载和水平荷载分别代入式(10)和式(11)，在单环管片范围积分，得到附加注浆压力引发的变形计算公式为

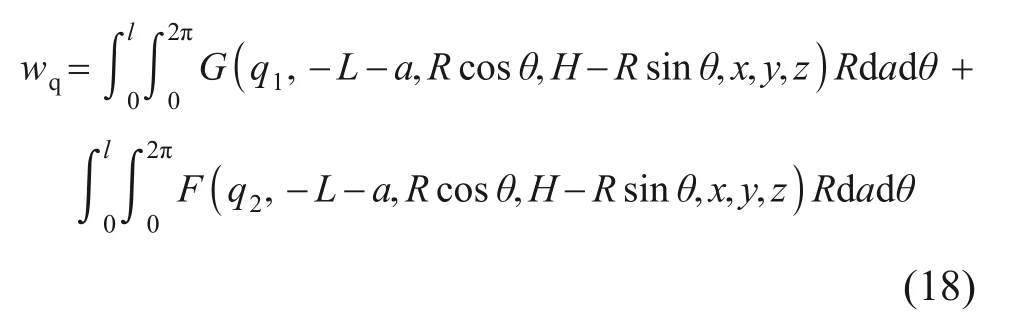
式中：l为单环管片长度，m；a为积分点到盾尾的距离，m。

叠加地层损失引发的地表变形及施工因素引发的地表变形，可以得到盾构机在曲线段掘进时引发周边土层沉降的计算公式：

3 邻近既有管线变形计算

计算外界扰动引起既有管线的变形时，一般将既有管线简化为放置在Double Pasternak 弹性地基梁上的Euler-Bernoulli 梁进行求解。Pasternak 地基梁模型考虑了土体间剪切层的影响，更符合实际情况，被广泛应用于地下管线变形计算[22−23]，其计算模型如图6所示。

图6 Double Pasternak 弹性地基梁Fig.6 Elastic foundation beam of double Pasternak

Pasternak地基梁模型的表达式如下：

式中：q(z)为盾构开挖时引起管线的附加应力，q(z)=kw；w为由式(18)计算得到的对应管线所在位置的土体竖向变形；wg(z)为管道竖向变形；Gc为剪切层的剪切刚度；k为地基基床系数，本文根据VESIC[24]提出的地基基床系数公式计算；Et为土体的弹性模量，MPa；ht为剪切层厚度，一般取管道直径的2.5 倍[6−8]；d为管道直径，m；EI为管道的等效抗弯刚度，其值可以根据张文杰等[25−27]提出的竖向等效连续化模型确定。

式(20)为四阶常微分方程，采用常规的方法难以直接求得其解析解，现阶段主要基于有限差分法进行求解。将管道在计算范围内离散为N+5 个单元，每个单元的长度为l，其中在计算范围边界各有2个虚拟节点单元。假定在计算范围外及边界处的管道单元不受开挖的影响，则两侧虚拟单元的位移为0，管道受力、变形及离散情况如图7所示。

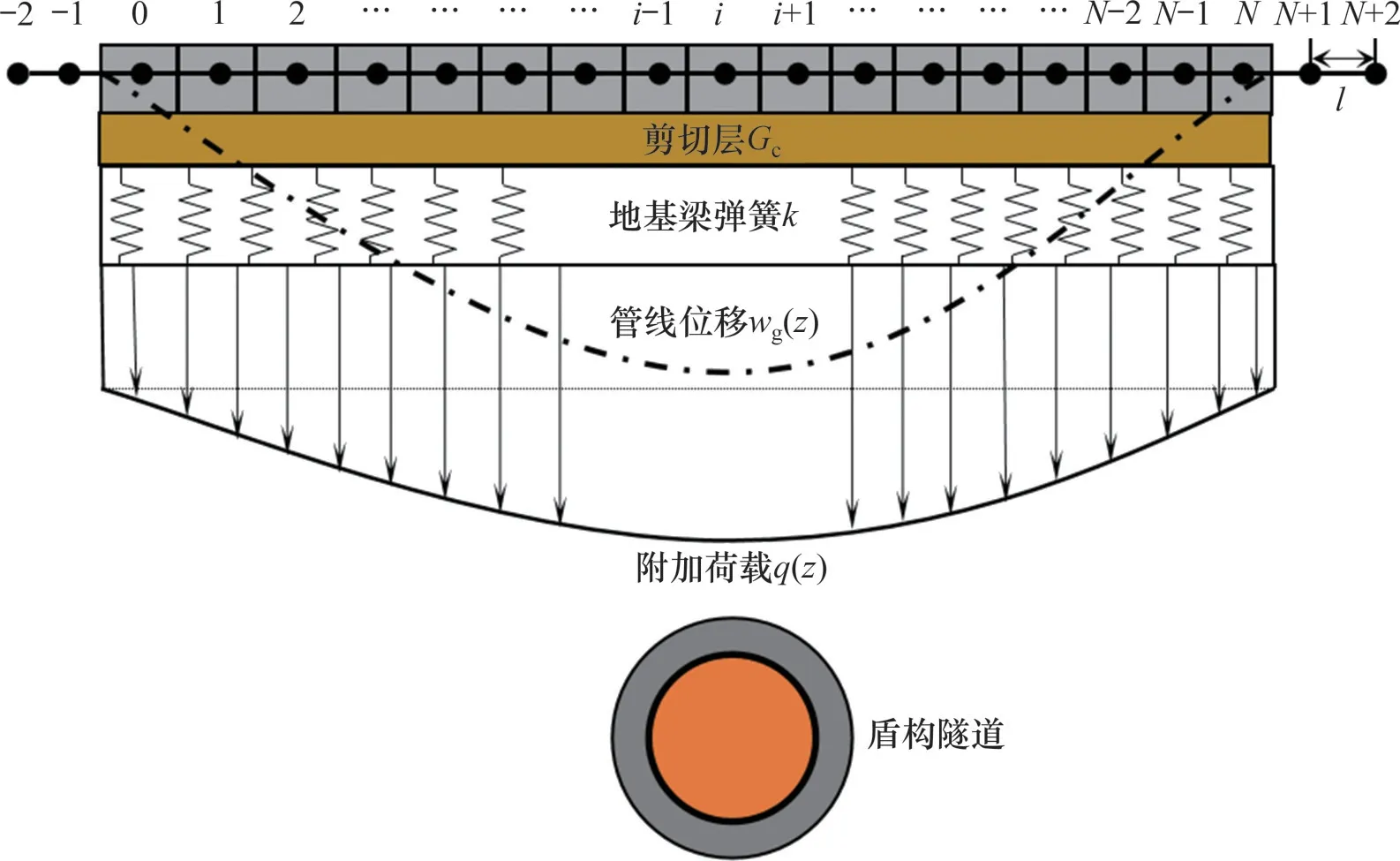
图7 管道离散处理Fig.7 Pipeline discrete processing

由边界处的弯矩和剪力等于0可以得到

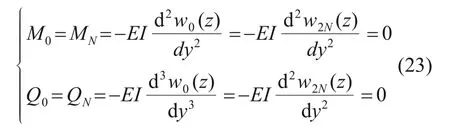
计算范围内的管道节点(0～N)，代入标准一阶中心差分公式，式(20)中四阶微分和二阶微分可以分别写为

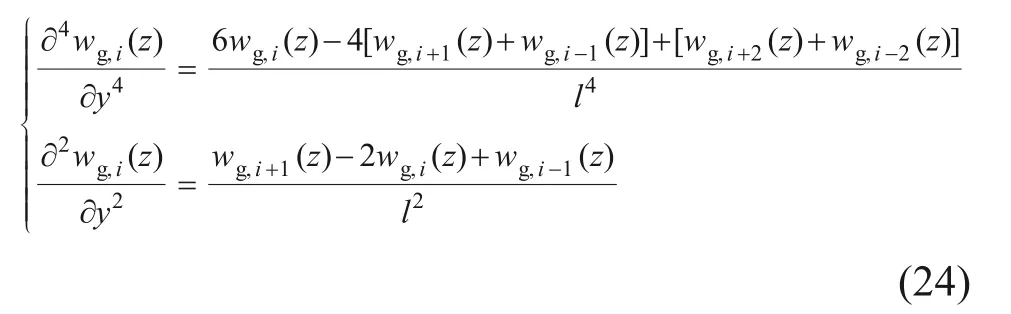
根据式(23)和式(24)，虚拟节点的位移表达式为

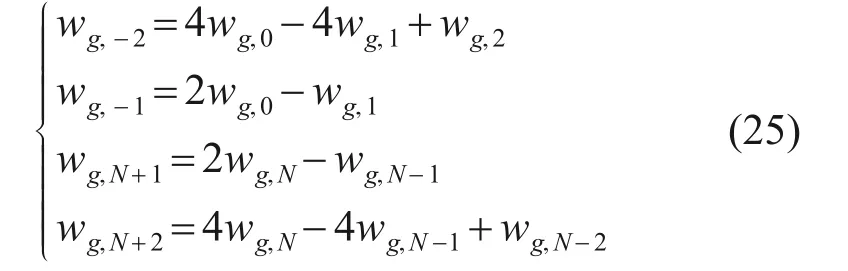
将边界条件公式(25)和降阶公式(24)代入式(20)，则可以将离散后的每个节点对应的高阶微分方程转化为连续方程，通过构造对应的矩阵则可以实现求解。管线节点的位移刚度矩阵方程可以表示为

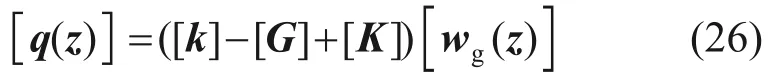
式中：[q(z)]为作用在节点上的附加荷载矩阵；[k]为土体基床系数矩阵；[G]为剪切层刚度矩阵；[K]为管道刚度矩阵；[wg(z)]为管线离散全部节点的变形矩阵。

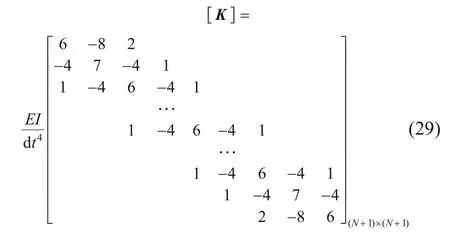
将式(27)，(28)和(29)以及各计算参数代入式(26)，即可求解得到盾构隧道曲线段掘进时引发既有管线的变形。

4 数值模拟验证

4.1 模型参数及边界

以某电力隧道工程为背景，此项目采用直径为4.4 m的土压平衡盾构机施工。为了满足线路走向的要求，掘进过程中多次采用曲线段施工，其中最小曲线段的曲率半径仅为150 m。隧道埋深为16 m，隧道直径为4.4 m，以本工程构建对应的数值计算模型。隧道两侧到模型边界取4倍隧道直径宽度，曲线段长度取100 m，构建的数值计算模型长×宽×高为40 m×100 m×33 m。管道位置位于曲线中段位置(x=0 m)，直径d=0.4 m，厚度为0.05 m，埋深h为4 m。盾构机始发于管线后方50 m(x=−50 m)，掘进至管线前方50 m(x=50 m)后停止，在x=0 m处掘进轴线与管线轴线正交。模型对应的边界条件如下：上表面为自由表面，固定底部位移，约束左右及前后4个面的法向位移。构建的数值模型情况见图8。

图8 模型及土层分层情况Fig.8 Model and soil layering

4.2 材料性质及参数

在数值模拟中，土体材料选用弹塑性体，破坏准则选用摩尔−库仑准则；管道及管片采用线弹性实体单元模拟[28]，其中，管道采用C20强度混凝土模拟，盾构隧道管片采用C25 强度混凝土模拟。由于在模型中没有考虑管道及管片的接头及非连续性，因此，需要折减管道和管片的刚度，根据等效连续化模型原理以及相关研究[25−27]，管道与管片的刚度折减系数分别为0.1 和0.05。盾壳内存有对应的支护设施且支护强度极高，因此，不考虑盾壳的变形，盾壳的刚度取管片的刚度的100 倍。模拟注浆作用时，在盾尾后方单环范围内(即存在附加注浆压力的范围内)，将浆液视为未凝固状态，此时，浆液的弹性模量为40 MPa，而在此范围之外，浆液视为凝固状态，弹性模量为300 MPa[28]。在计算模型中预留超挖间隙单元，如图9所示，模拟曲线段超挖时只需将对应部分单元移除。对应的理论计算参数和模型采用的参数见表1和表2，其中，理论计算中对应的参数为现场施工段试验测量所得的参数均值，土层参数取值为隧道覆土的加权平均值。数值模拟中土层参数按照图8取值。

表1 盾构施工参数计算参数Table 1 Calculation parameters of shield parameters

表2 土体及管道计算参数Table 2 Calculation parameters of soil and pipe

4.3 掘进荷载施加情况

在模拟中，由于需要在开挖面和盾壳处施加非均匀荷载，因此，在构建数值计算模型时，将刀盘和盾壳划分成2部分，如图9所示。需要注意的是，刀盘处的推力和盾壳处的摩阻力随着深度变化而变化，为了实现荷载随深度变化的要求，本文提取刀盘和盾壳单元范围内的全部单元节点，确定对应节点的深度，计算得到对应的土压力荷载，并通过编制的Fish 函数关联附加荷载或荷载计算公式，最终将完整的荷载施加在对应节点位置。模拟附加注浆压力时，将注浆压力施加在浆液未凝固区域，浆液凝固区域视为未受到附加注浆压力荷载的作用。

图9 盾壳模型及荷载施加Fig.9 Shield shell model and load application

4.4 地表沉降对比分析

图10所示为盾构机掘进至x=0.4 m(开挖至42环)时的地表沉降云图。在实际施工中，对盾构机掘进过程中地表沉降进行监测，分别监测横向地表沉降和沿隧道掘进轴线的地表沉降情况，在数值计算模型中布置相同位置的测线，如图10所示。

图10中x=0 m 对应刀盘附近处测线，x=10 m对应刀盘前方10 m 处测线，x=−10 m 对应刀盘后方10 m 处测线，y=0 m 对应沿盾构机掘进轴线的测线。从图10可以看到：在测线x=0 m 及测线x=−10 m 地表产生沉降变形，在测线x=10 m 地表产生隆起变形。提取对应的沉降值并与其理论计算结果、数值模拟计算结果以及现场监测结果进行对比，结果如图11所示。从图11可以看到：

图10 开挖至x=0 m时沉降云图Fig.10 Settlement cloud diagram when excavation reaches x=0 m

图11 横向及纵向地表沉降曲线对比Fig.11 Comparison of transverse and longitudinal surface settlement curves

1)地表沉降理论预测公式计算结果、数值模拟计算结果与现场的监测结果相差较小，验证了计算模型及计算公式的正确性。同时，在盾壳后方，地表沉降理论预测公式计算结果相比数值模拟及现场监测结果较小，其主要原因是理论计算中未考虑注浆浆液的流动及凝固情况，导致预测结果与计算结果有所偏差。

2)盾构机在曲线段掘进时，地表横向沉降呈非对称分布，横向地表沉降最大沉降位置出现在弯道内侧，偏离刀盘中心线，而直线段掘进时，地表横向沉降分布通常关于刀盘中心线对称[4−8]。

3)直线段理论计算结果普遍小于其余3种方法所得结果(见图11(b))，其主要原因是直线段未考虑超挖引发的地层损失。

4)地表最大值沿盾构隧道掘进轴线分布呈“S”形，在刀盘前方地表会发生轻微隆起，最大隆起量约为2 mm；在刀盘处及后方地表发生沉降，最大沉降量约为24 mm，位于盾尾间隙的后方。

4.5 管道变形分析

从图11(b)可以看到：当盾尾通过时，地表沉降值达到最大，此时，盾构施工因素对周边环境的扰动达到最大。为此，本文提取盾构机掘进至管道前方8.8 m(掘进49 环)时管道的变形情况，结果如图12所示。

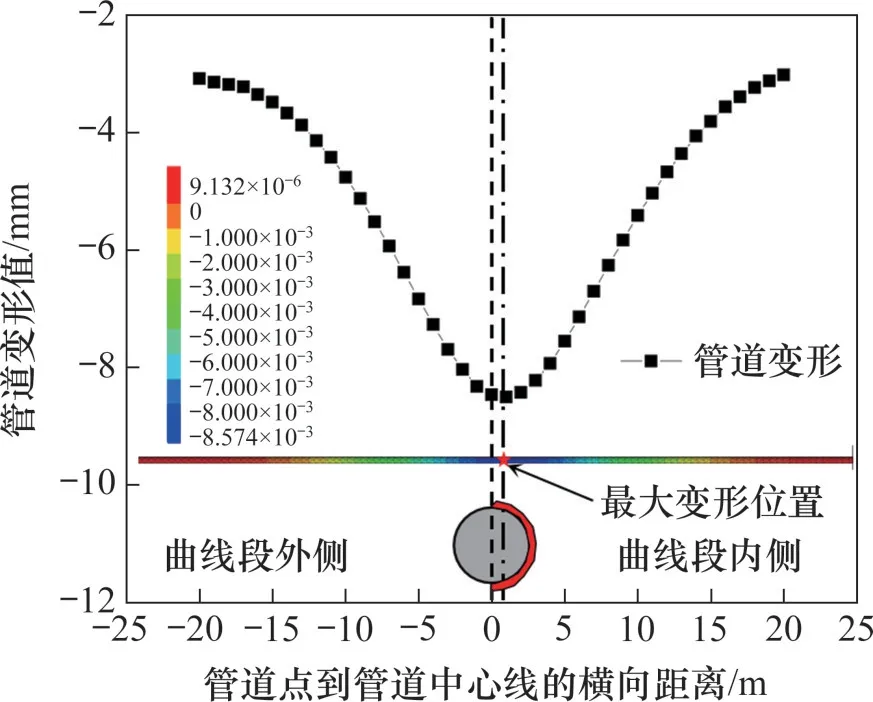
图12 盾尾通过后管道变形情况Fig.12 Deformation of pipe after passage of shield tail

从图12可以看到：管道最大沉降值为8.5 mm，最大沉降位置偏向曲线内侧，位于距刀盘中心线1 m左右的位置。

为了验证理论公式结果的正确性，分别提取当盾构机掘进至管道后方15.2 m(开挖至第29环，x=15.2 m)，8 m(开挖至第35 环，x=8 m)，管道前方8.8 m(开挖至第49，x=−8.8 m)以及管道前方16 m(开挖至第55环，x=−16 m)时的地表沉降，其数值模拟计算结果与理论计算结果对比如图13所示。

图13 管道横向变形曲线对比Fig.13 Comparison of transverse deformation curves of pipeline

从图13可以看到：管道变形值理论计算结果与数值模拟结果误差较小，证明了理论公式的正确性；盾构机未通过管道时，会导致管道产生轻微隆起，最大隆起位置位于管道中心线；当盾构机通过管道后，管道会产生沉降，此时，最大沉降位置出现在曲线内侧，偏离管道中心线；随着盾构机持续掘进，最大沉降位置又将回归至管道中心线；当盾构机掘进至管道前方8.8 m时，管道沉降变形达到最大值，此时，理论计算结果为8.20 mm，数值模拟计算结果为8.50 mm，两者较吻合，且这2 种计算方法所得计算结果均表明管道最大变形位置位于曲线内侧，偏移管道中心线约1 m。

通过编写的监测Fish 语言提取管道最大沉降随盾构机刀盘与管道距离的变化情况，管道最大沉降理论计算结果与数值模拟结果对比如图14所示。从图14可以看到：

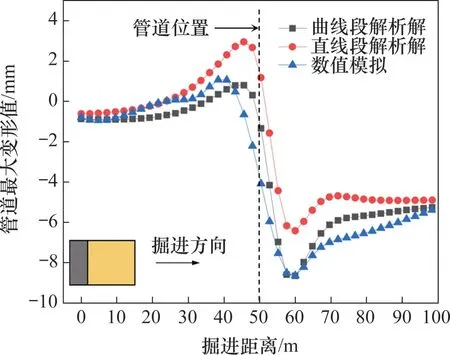
图14 管道纵向变形曲线对比Fig.14 Comparison of longitudinal deformation curves of pipeline

1)管道最大沉降理论计算结果和数值模拟结果分布规律一致，随着盾构机与管道之间的距离减小，管道逐渐隆起；当刀盘距离管道8 m 左右时，管道隆起量达到最大，最大隆起量约为1 mm；随着盾构机逐渐推进，地层损失造成的扰动逐渐增加，管道开始由隆起变形转变为沉降变形；当盾构机掘进至10 m 时，既有管道处于盾尾间隙的后方，管道沉降值达到最大，最大沉降约为8.6 mm，随后管道沉降值开始回升，并逐渐趋于稳定。

2)管道最大沉降理论计算结果与数值模拟结果在盾构机未通过管道前的吻合度比通过后的吻合度高，其主要原因可能是数值模拟中考虑了注浆浆液凝固的作用，虽然赋予了注浆区域相应的强度，但此部分仍存在变形，而在理论计算过程中未考虑浆液凝固的影响，导致管道最大沉降数值模拟结果大于理论计算结果。

5 管道沉降的影响因素敏感性分析

以第4节中情况为背景，假定既有管线位于盾尾间隙的上方(x=−8.8 m)，转弯半径R0为150 m，分别改变管道弹性模量E、转弯半径R0以及隧道半径R，研究以上因素对管道沉降的影响。

5.1 管线模量E

管线采用的材料一般有PVC材料、混凝土材料以及钢材，假定管线材料为C20混凝土，分别令管线弹性模量E为2 300 MPa(PVC材料)，25 500 MPa(C20混凝土)，28 000 MPa(C25混凝土)，30 000 MPa(C30混凝土)和230 000 MPa(钢材料)，且假定不同材料的刚度折减系数一致，管线变形随管线弹性模量的变化如图15所示。