深水聚焦波群的双层Boussinesq数值模拟
2022-09-21刘必劲张振伟刘忠波
刘必劲,张振伟,刘忠波
(1.浙江大学海南研究院,海南三亚 572025;2.厦门理工学院土木工程与建筑学院,福建厦门 361024;3.大连海事大学交通运输工程学院,辽宁大连 116024)
0 引 言
畸形波是非线性极强的瞬态大浪,受实际海洋中各种不确定的众多环境因素影响,导致人类对这种畸形波的产生机制并没有完全掌握。当这种瞬态大浪作用在过往的船只或海上建筑物时,将会严重影响它们的安全。为了探求畸形波的生成机制,国内外学者尝试从相位聚焦、波-流非线性相互作用、地形聚焦作用、表面风的作用、波浪调制不稳定性等方面开展畸形波的研究。
对畸形波的研究主要方法有物理模型实验室模拟[1-5]、数值模拟[6]和理论分析[7-8]等。近年来,伴随计算机性能的大幅度提升和各类数值模型的不断完善,采用数值模型开展畸形波的研究成为比较常见且主要的手段,其中时域计算模型多采用势流理论、欧拉方程或粘性流理论等。在势流理论方面,有高阶边界元求解Laplace 方程的数值模型[6]、高阶谱数值模型[9-11]和Boussinesq 型水波数值模型[12-13]。欧拉方程或粘性Navier-Stokes方程基础上建立起来的非静压模型[14],将内部造波法引入CIP求解对流项的Navier-Stokes 方程的数值模型[15]。相关研究表明,采用相位聚焦方式可以形成畸形波,由于畸形波的强非线性特征,线性理论和二阶Stokes波理论均无法精准预报聚焦波面和波峰面下的速度场[1]。
聚焦波演化形成畸形波的过程中,多种频率组成成分的波浪非线性相互作用引起的多波共振或调制不稳定等是生成畸形波的最有可能的原因之一。精确预报畸形波的生成与发展过程势必要求数值模型具有足够精准的色散性和非线性特征。一方面,聚焦波中波浪频率组成成分越多,在同一水深下,这些波浪具有不同的无因次水深,要求模型在更大水深范围内具备优良的线性色散特性,才能保证每一种频率波浪的计算结果与线性解析解具有良好的相位匹配关系[16];另一方面,不同频率的波浪之间存在较为明显的非线性相互作用,这将产生低频、高频等其他频率的差频与和频波浪,精准的非线性特征(二阶和差频、三阶非线性波幅、波幅色散)则可以保证数值模型在模拟非线性波浪传播时具有较好的适用性[16-19]。当方程在描述速度分布的精度不准确时,数值计算得到的速度场与相关实验结果会出现一定的差异[13]。刘必劲等[13]采用Liu 和Fang[20]的单层Boussinesq 型水波数值模型,在开展聚焦波的数值模拟时发现,聚焦波面与试验结果的吻合程度良好,但聚焦波峰值下的水平速度场计算值呈S 形,与Baldock 等[1]试验的速度分布对比时仅基本吻合,这表明受限于单层Boussinesq 水波型方程在速度分布方面的精度,该数值模型无法胜任深水聚焦波速度场的模拟。为此,本文选用了Liu 和Fang[20]的双层Boussinesq 型方程,建立相应的数值模型,研究该数值模型在应用于模拟深水聚焦波问题时,波面位移特别是聚焦波峰下水平速度的准确性。
1 双层Boussinesq数值模型
1.1 控制方程
在无旋、无粘的假设下,Liu 和Fang[20]保留了垂向速度,经推导给出了适合缓变地形的双层Boussinesq 方程,立面二维模型由9 个方程组成,含有9 个独立待求变量:波面位移η、自由表面处水平和垂向速度uη和wη、静止水位处的速度u0和w0,以及计算速度(u*i,w*i)(i=1,2)。方程的具体表达形式如下:
在自由面处,满足精确的运动学边界条件和动力学边界条件:

自由面处速度与静止水位处速度之间的表达式为
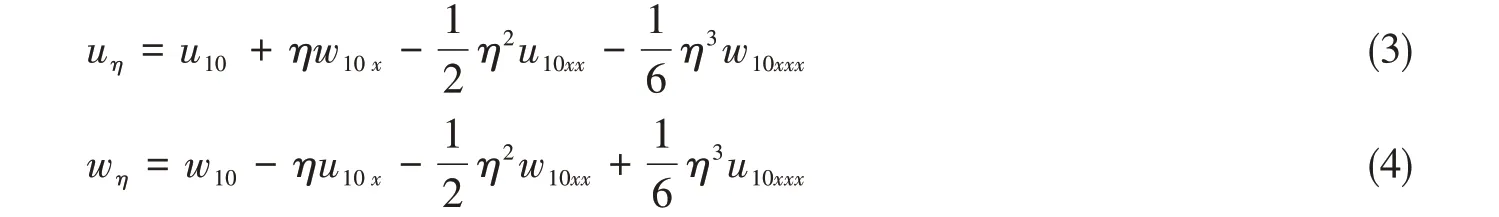
静止水位处速度与第一层计算速度的关系式为
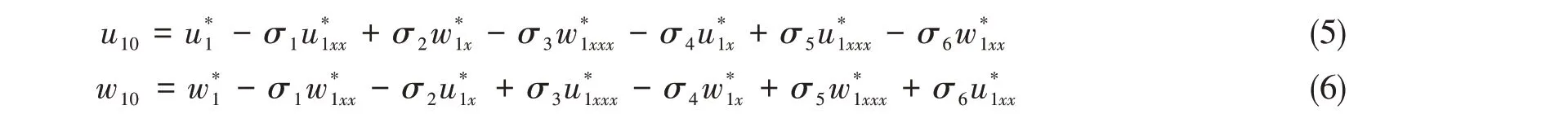
在连接水深位置处,满足速度连续,则有

在水底处,满足运动学边界条件:
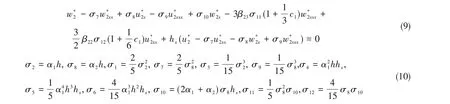
式中,下标x表示对空间x求导,g是重力加速度。
方程(1)~(9)构成了本文数值模型对应的双层Boussinesq水波方程,该方程具有较好的线性与非线性性能。对波浪沿水深分布的速度进行优化,Liu等[18]给出了方程中的系数(α1,α2,β12,β13,β22,β23)=(0.129,0.371,0.941,0.896,0.948,0.608)。
1.2 数值模型的求解
双层Boussinesq 水波方程的最高空间导数是3,其与目前常用于海岸波浪模拟的开源程序FUNWAVE[21]对应的Boussinesq 水波[22]方程最高空间导数的阶数上是一致的。为此,该方程在时空差分格式的离散上均采用与该开源代码一样的数值格式。在时间差分格式上,采用混合4 阶Adams-Bashforth-Moulton 格式。其中,预报时利用3 阶Adams-Bashforth 格式求解方程(1)和(2),可以得到波面位移以及波面处水平速度的预报值;分别求解方程(3)、(5)和(7)可得到3个水平速度的预报值;进而求解方程(9)、(8)、(6)和(4),可依次得到4 个垂向速度的预报值。校正时则利用4 阶Adams-Moulton 时间步进格式,得到波面位移以及波面处水平速度的校正值,其他速度变量校正值的求解过程类似于预报阶段,不同点在于所有方程右端项均是当前预报层的值。当9 个变量的校正值与预报值之间的误差控制在0.000 1 内,当前迭代结束,否则更新变量的预报值,其采用校正值和预报值的加权值,继续进行当前步的迭代过程。校正值的加权系数R为0.05~0.1,而预报值加权系数为1-R。
2 数值模型的验证
本章将重点研究聚焦波的一些特性,并与相关理论解析解和实验结果进行比较,验证本文数值模型的适用性。首先开展线性聚焦波的模拟,考察数值模型在具有多个不同周期组成下线性色散的适用性问题,其最重要的表现是叠加后波面的相位问题,当多波组成的波面与解析波面一致时,则表明数值模型在更大无因次水深范围内有较好的色散精度;其次,开展非线性深水聚焦波的模拟,考察数值模型波-波非线性相互作用和非线性色散的精确性问题。
2.1 线性聚焦波的模拟
双层Boussinesq 方程具有确切的色散关系表达式,其与Stokes 波色散关系表达式的对比在Liu 和Fang[20]以及Liu 等[18]中均明确给出,本文的双层Boussinesq 数值模型中采用了Liu 等[18]给出的参数值,原图可详见Liu 等[18]中的图3,这里为了展现其色散性能对图进行了放大,重新绘制得到的无因次相速度见图1。由图1 可见,方程的相速度在无因次水深0<kh<20范围内与解析解的误差仅为0.003 68%,这表明双层Boussinesq 水波方程具有极为精确的色散特征。尽管方程具有精确的色散关系式,但数值模型因离散误差以及数值积累误差等,一般来说,其计算出来的色散方面的性能低于理论分析得到的色散性能。
当忽略非线性项后,双层Boussinesq 模型退化为线性模型,利用该模型对线性聚焦波进行模拟,目的是考察建立的双层Boussinesq 数值模型的精准度,这里选择Baldock 等[1]给出的波浪频率进行数值计算。Baldock等[1]的聚焦波深水实验含有不同波浪频率段范围,在不同周期段内等分周期成29份,每个频率波幅取值相等,其中的B 组(T=0.6~1.4 s,宽谱)和D 组(T=0.8~1.2 s,窄谱)对应的线性无因次水深kh分别为1.568~7.825 和2.026~4.403。在数值模拟中,水深为0.7 m,计算域设置为24 m,末端设置4 m长的海绵边界层吸收波浪,时间步长为0.01 s,空间步长为0.04 m。设置线性聚焦位置在8 m,线性聚焦时间为60 s,聚焦波幅为0.055 m,选择这一聚焦时间点的原因是避开数值模型在模拟波群演化中波前(wave front)的影响。在聚焦时刻t=60 s,B 组和D 组的计算结果与一阶Stokes 波解析解的比较见图2 和图3。由图可见,数值模拟结果与解析解吻合程度高,这一方面表明数值模型可以精准捕捉不同频率波浪的相位,另一方面也从数值角度佐证了如图1展示的双层Boussinesq水波方程在较大频率范围内精准的相速度。此外,在聚焦位置处,两组工况的计算波峰面均是0.054 7 m,与解析波峰面0.055 m的误差是0.5%。
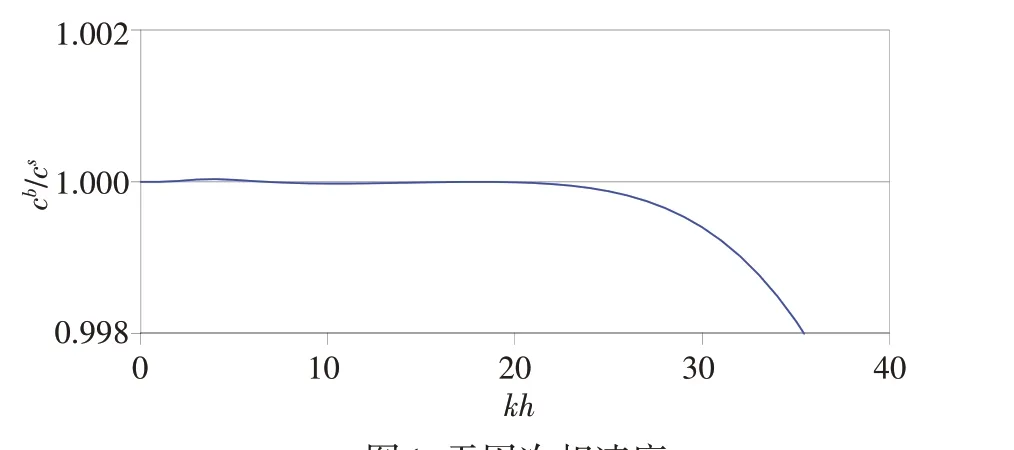
图1 无因次相速度Fig.1 Non-dimensional phase velocity
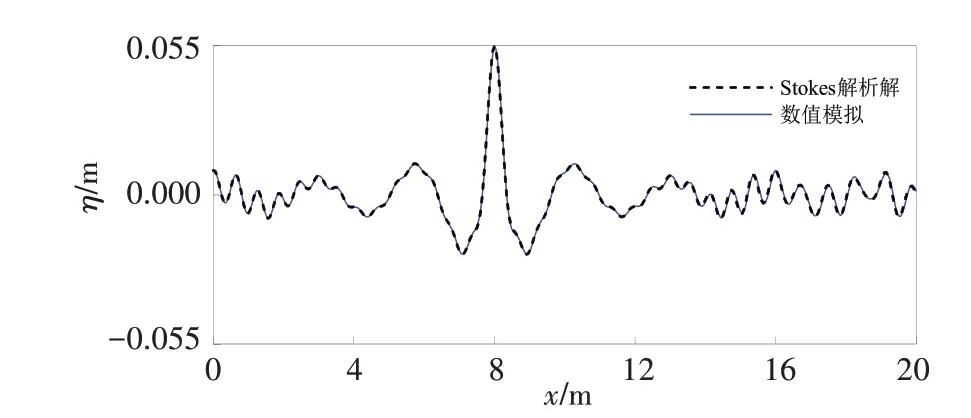
图2 B55计算结果与Stokes波解析解的比较Fig.2 Comparison of the simulated surface elevation with the analytical solution for Case B55
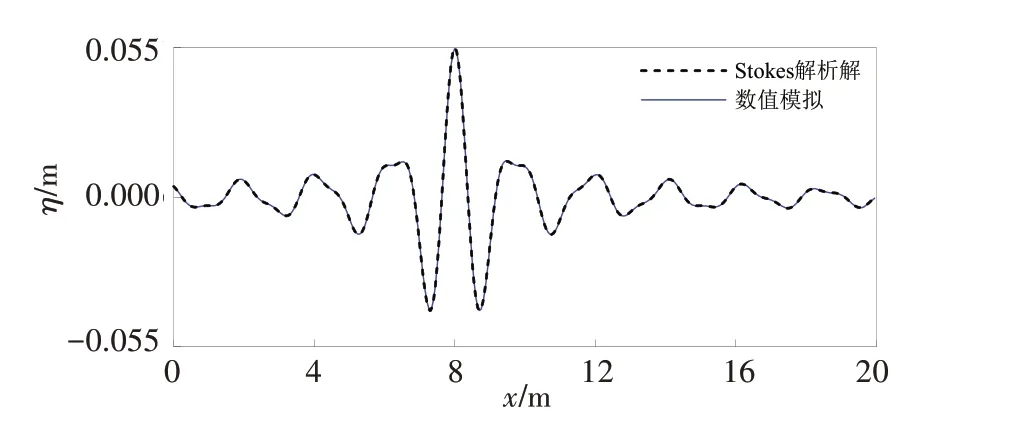
图3 D55计算结果与Stokes波解析解的比较Fig.3 Comparison of the simulated surface elevation with the analytical solution for Case D55
2.2 非线性聚焦波的模拟
在2.1 节线性聚焦波的模拟中,不同成分的线性波浪满足叠加关系,以上仅是表征方程在线性波群中相位捕捉的能力。实际中,非线性波浪并不满足线性叠加原理。一方面,聚焦波组成成分之间存在明确的非线性相互作用,这会导致波群演化过程中出现多个频率之间产生和频项与差频项,因此,要求方程必须具有足够精确的和频与差频性能;另一方面,根据三阶Stokes波理论可知,波幅越大,波长将越长(同等条件下),在相位聚焦生成大波的过程中,波峰面越大,将会导致其与设置的线性聚焦位置发生更多偏离[1,14]。
在进行数值模拟之前,首先确认方程的非线性和速度分布特征方面的适用范畴。在1%误差下,双层Boussinesq 水波方程在二阶非线性、三阶非线性和波幅色散三个特性方面的最大适用水深kh是35.7、33.1和36.7,而线性水平速度和垂向速度的最大适用水深kh均是17.6,关于这些特性对应的详图可见参考文献[18]。这表明双层Boussinesq 数值模型可以胜任深水聚焦波演化的模拟。其次,对所采用的聚焦波物理试验进行说明。第一,水槽中开展的波浪试验,波高在沿程方向存在一定程度的衰减现象;第二,造波机驱动信号产生的波浪与理论解存在差异;第三,实际水槽无法克服边界的反射问题,这种反射波会“污染”试验结果。
针对Baldock 等[1]试验中B 组和D 组的系列工况开展数值模拟研究,在计算中,数值水槽长24 m,末端设置4 m 的海绵边界层消波。空间步长和时间步长分别是0.04 m 和0.01 s,计算时间为40 s。对B 组和D 组分别含有三组线性聚焦波峰面Af(分别是22 mm、38 mm 和55 mm)工况进行数值模拟。在入射边界,造波采用线性波浪条件,设置的线性聚焦位置是8 m,通过反算可以确定入射波浪的情况,聚焦时间设置为30 s,其他条件均与Baldock 等[1]实验描述的一致。实际计算得到的最大聚焦位置处,波面位移与实验结果[1]的对比见图4。相应地,最大聚焦波峰面下的水平速度与实验结果的对比见图5。从图4中可见:非线性较强的工况B55和D55的计算结果比实验结果大;作为非线性相对弱一些的D38 工况,计算波面比实验结果小,其他非线性工况计算结果与实验结果相差不大。从图5 对比的水平速度场来分析,除D22 外,其他模拟结果与实验结果的吻合程度较好,同时双层模型计算的速度剖面比较光滑,不会出现单层模型给出的S 形[13],这表明双层Boussinesq 水波方程具有良好的速度分布特性。
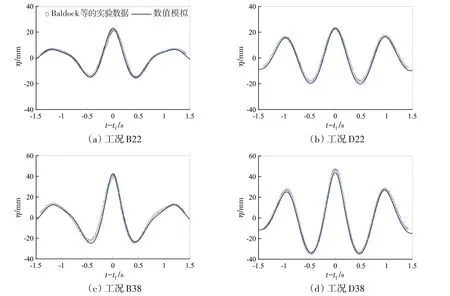

图4 计算波面位移与Baldock等[1](1996)实验结果的对比Fig.4 Comparison of the calculated surface elevation with the experimental results of Baldock et al[1](1996)

图5 水平速度与Baldock等[1](1996)实验结果的对比Fig.5 Comparison of the calculated horizontal velocity with the experimental results of Baldock et al[1](1996)
此外,实验中流速仪无法捕捉到波峰面处的速度,而数值模型可以提供波峰面速度,因此,速度场的最大值高于试验值是可以接受的。所有工况算例表明,双层Boussinesq数值模型可以较为准确地模拟深水聚焦波演化和垂向分布的速度场。
根据前面提及水槽实验中的波高衰减等问题,对两组非线性最强的两个算例(B55和D55)减少入射波高进行模拟,其中,B55工况对应的线性聚焦波峰面Af设置为0.053 m,而D55工况对应的Af设置为0.053 5 m,具体计算得到的波面位移和水平速度结果见图6。由该图可见,计算的波面位移和水平速度均与实验结果吻合。
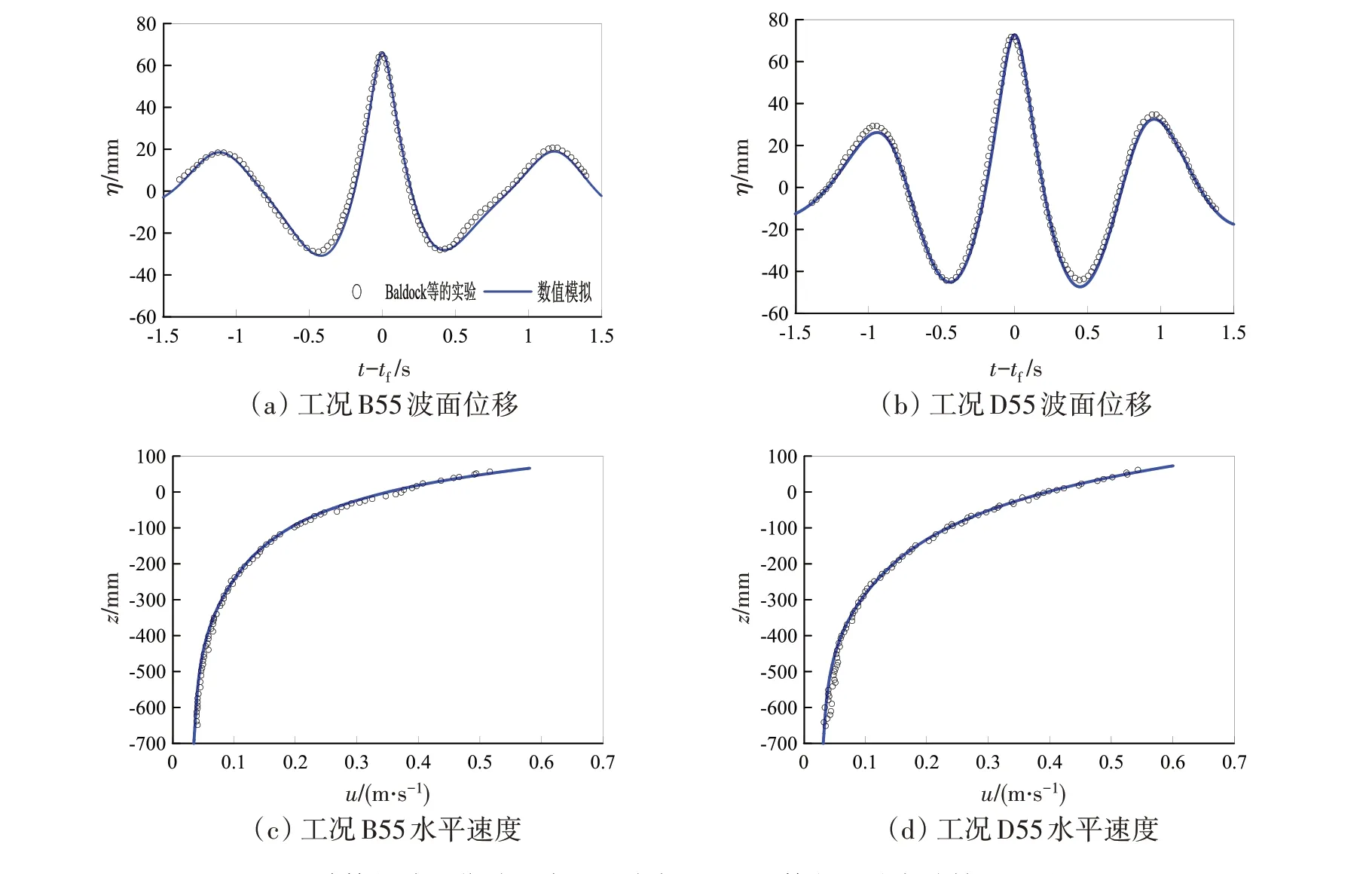
图6 计算的波面位移和水平速度与Baldock等(1996)实验结果的对比Fig.6 Comparison of the calculated surface elevation and horizontal velocity with the experimental results of Baldock et al(1996)
3 数值模拟结果的进一步讨论与分析
从已有的实验研究[1]和相关数值模拟研究[6,13]可确知,保持中心频率不变,在同样线性聚焦峰面情况下,周期范围越宽,则非线性越弱。因此本文以D组为例,首先与Baldock等[1]的实验条件类似,保持线性聚焦位置与聚焦时间不变化,讨论本文建立的双层Boussinesq数值模型计算得到的最大波面位移ηf和最大波面位移处的水平速度uf随线性聚焦波峰幅值Af的变化情况;其次,以Baldock 等[1]的D55 为例,讨论线性聚焦位置(xf=6 m,7 m,8 m,9 m,10 m)对ηf和uf的影响,同时为避免短波没有传播到聚焦位置等对数值结果的影响,数值模型中将线性聚焦时间tf设置为35 s。最后,仍以Baldock 等[1]的D55为例,讨论了计算域内每个空间点的最大波峰面位移η和对应η处的水平速度uη。
在数值模拟中,保持水深为0.7 m,计算域仍然设置为24 m,末端设置4 m 长的海绵吸收边界,时间步长为0.01 s,空间步长为0.04 m,计算时间设置为40 s。
3.1 线性聚焦波峰幅值Af对ηf和uf的影响
图7和图8分别给出了D组系列工况中的最大波面位移ηf和最大波面位移处的水平速度uf随线性聚焦波峰幅值Af(0.01~0.055 m,每个工况间隔0.005 m)的变化情况。由图7 可见,数值模型计算的最大波峰面在不同工况时与实验结果[1]趋势基本一致且比较接近;进一步分析可知,伴随线性聚焦波峰面(入射波高)的增大,最大波峰面呈现非线性变化。类似地,图8给出的最大波峰面处的水平速度也具有同样变化趋势。
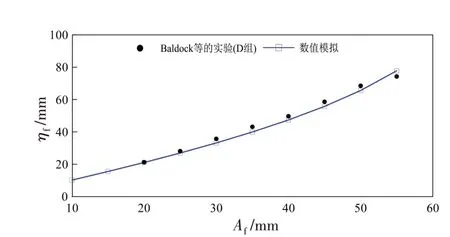
图7 最大波面位移随线性聚焦波峰幅值的变化Fig.7 Variation of the maximum surface elevation with the amplitude of the linearly focused wave crest
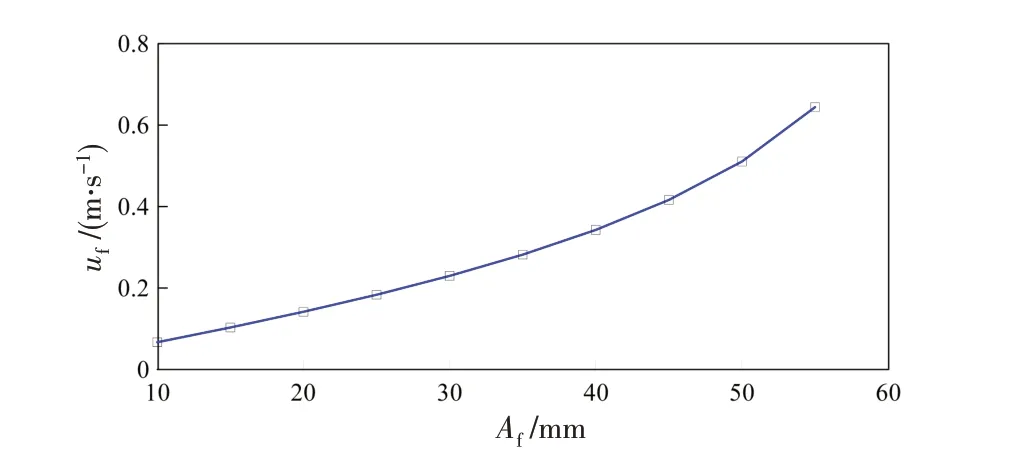
图8 最大波峰面处水平速度随线性聚焦波峰幅值的变化Fig.8 Variation of horizontal velocity at the maximum surface elevation with the amplitude of the linearly focused wave crest
3.2 线性聚焦位置xf对ηf和uf的影响
表1 给出了Af=55 mm 工况(tf=35 s)最大波面位移ηf和最大波面位移处的水平速度uf随线性聚焦位置(xf=6 m,7 m,8 m,9 m,10 m)的变化情况。在表中也给出了相邻两次大波峰面之间的传播速度cf,其计算公式可写为

表1 ηf和uf随xf的变化情况Tab.1 Variation of ηf and uf with xf

式中:xf1和xf2分别为相邻两次的最大波峰面位置,对应着时间tf1和tf2;xf1为设置线性聚焦位置后的第一个聚焦波峰面位置,xf2为相邻的最大波峰面位置。需要强调的是,从数值计算结果来看,xf2可以在xf1之前,也可以在xf1之后,根据具体的数值模拟情况确定。
由表1 可知:一方面,伴随线性聚焦位置的增大,线性聚焦位置后的第一个聚焦波峰面位置xf1处的波面和对应的水平速度值均在增大,且变化范围较大;另一方面,较短的距离范围内,不同频率之间的非线性相互作用还未充分发展。因此,在线性聚焦位置为xf(5m,6m 和7m)的第1次聚焦之后,又出现了更大的聚焦波峰面,在本文计算中并未发现其后有第3 次聚焦大峰。而在其他算例(xf=8m,9m,10 m 和12 m)中,均在最大聚焦位置前,也出现了较大的聚焦波峰面(可以近似认为是局部最大波峰)。综合来看,所有计算工况全域内的最大波峰面在74.42~81.27 mm 之间,这说明线性聚焦位置的设置对计算的最大波峰面产生了较大影响;类似地,所有计算工况中最大波峰面处的水平速度变化范围为0.596~0.702 m/s之间,说明线性聚焦位置的设置对uf也产生了较大影响。此外,有趣的是式(10)给出的相邻两次最大波峰面间的传播速度cf却变化很小,其变化范围在0.79~0.81 m/s之间。所有工况中,波峰面的最大速度为0.702 m/s,其小于最大波峰间的传播速度0.81 m/s,这间接表明本文计算工况中波浪均未发生破碎。
3.3 波峰面最大值及水平速度的沿程变化
针对Baldock等[1]的D55工况,计算得到的波峰面及水平速度的沿程变化见图9和图10。从图9中可知,以70 mm为界,存在较多的空间点波峰面超过该值,且存在一个较大的共振区域。类似地,图10也表明,波峰面处的水平速度也存在一个较大区域内的共振现象。
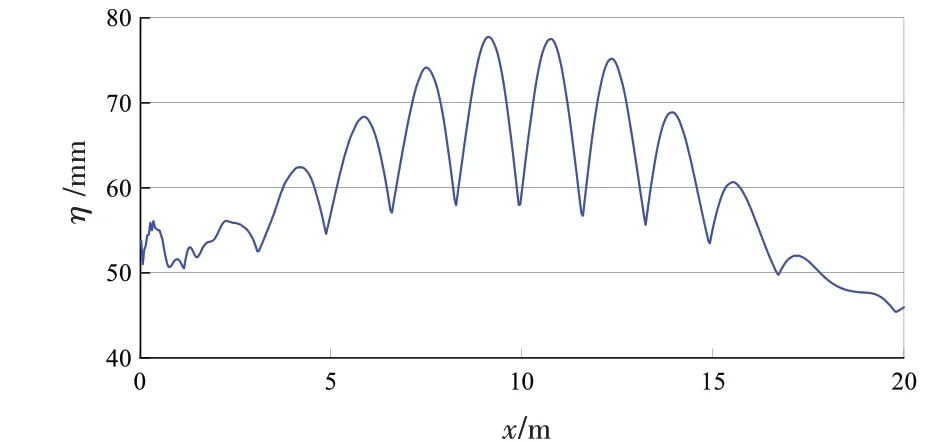
图9 波峰面最大值的沿程变化Fig.9 Maximum crest elevations along the flume
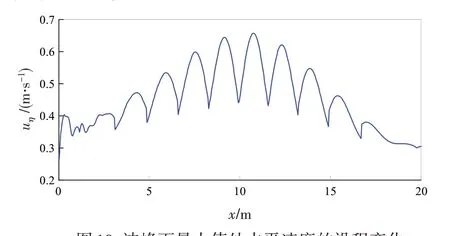
图10 波峰面最大值处水平速度的沿程变化Fig.10 Horizontal velocity of maximum crest elevations along the flume
4 结 论
本文基于双层Boussinesq 水波方程建立了聚焦波立面二维数值模型,将其应用于深水聚焦波的数值模拟中,得出的主要结论如下:
(1)数值模型计算线性聚焦波面处的波面位移与一阶Stokes波解析解吻合程度很高,表明本文建立的双层Boussinesq数值模型能够精确捕捉线性相位问题。
(2)非线性聚焦演化中,波浪非线性起重要作用,数值模拟波面与实验结果吻合较好,表明双层Boussinesq数值模型能胜任聚焦波波面演化的模拟,也印证了数值模型对应的方程具有良好的非线性特性。此外,对波峰面下的水平速度场,本文建立的双层Boussinesq数值模型也能较好地模拟。
(3)在强非线性波浪聚焦过程中,将会出现一个较大范围的波浪聚焦区。以Baldock 等(1996)的D55 为例,在设置不同线性聚焦位置的情况下,最大波峰面的传播速度保持在0.79~0.81 m/s 之间,这表明不同线性聚焦位置的设置对最大波峰面的传播速度影响不大,但其对波峰面下的速度影响较大。
