改进人工势场法的AGV路径规划算法研究

牛秦玉，李美凡，赵勇

(西安科技大学机械工程学院，陕西西安710054)

0 前言

路径规划是指AGV根据给定地图，通过某些指令要求，搜索出一条从起始点到目标点的无碰撞路径。常用的路径规划算法有：人工势场法、遗传算法、RRT算法、A算法等。其中，人工势场法以计算量小、实时控制性好、规划出的路径相对平滑等优点被广泛使用。

传统的人工势场法存在局部极小值和目标不可达的问题，为解决这两大问题，国内外学者做了大量的研究。文献[9]提出模糊人工势场法来解决局部极小点问题；文献[10]将免疫算法与人工势场法结合来解决局部极小值问题；文献[11]采用混沌优化方法对传统人工势场法的局部极小值和目标不可达问题进行优化；文献[12]引入了预测距离，在机器人未陷入局部极小值之前设置虚拟目标点，牵引机器人逃离局部极小值陷阱。

上述文献大多直接对人工势场法两大缺陷进行优化，当实际行车环境复杂、障碍物密集分布时，AGV极易陷入障碍物陷阱，导致路径规划失败。在上述研究基础上，本文作者考虑到实际行车环境中道路边界对路径规划的影响，将道路边界障碍化，在障碍物密集区域对障碍物进行连锁处理，使AGV能够成功逃脱障碍物陷阱，在此基础上再对传统人工势场法存在的目标不可达和局部极小值问题进行优化。

1 传统人工势场法

人工势场法起源于1986 年，它最初被KHATIB博士用于解决机械臂的运动规划问题。该算法的思想是以物理学中的抽象势场为基础，将AGV的运行环境抽象为势场空间，目标位置产生一个引力场，障碍物附近产生一个斥力场。AGV同时受到引力场产生的引力和斥力场产生的斥力，在二力的共同作用下朝目标点前进，最终规划出一条从起始点到目标点且无碰撞的路径。

常见的人工势场法中，引力势场函数的具体形式可表示为

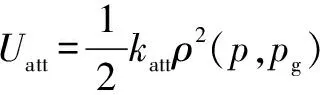
(1)

式中:为引力势场正比例系数；为AGV坐标位置；为目标点坐标位置；(,)为AGV与目标点之间的距离。

由引力势场的负梯度得到引力：

=-grad[]=-(,)

(2)

AGV离目标点越远，受到目标点的吸引力就越大；相反，当AGV离目标点很近时，此时AGV受到的吸引力几乎为零。AGV所受到的吸引力随着它与目标点之间的距离增加成正比增加。

斥力势场函数具体形式可表示为

(3)

式中:为斥力势场正比例系数；为障碍物坐标位置；(，)为AGV与障碍物的距离；为障碍物的影响范围。

由斥力势场的负梯度得到斥力：

=-grad[]=

(4)

与目标点相反，在障碍物影响范围内，障碍物对AGV的斥力随着两者之间距离的增大而逐渐减小。为障碍物对AGV产生斥力的最大影响范围，当两者之间的距离大于时，斥力场为0，对应产生的斥力也为0。

如图1所示，AGV在势场中所受合力为=+，AGV沿着合力的方向向前移动，该力决定了AGV的运动。当AGV逐渐接近目标点时，所受合力也逐渐减小，AGV到达目标点时所受合力变为零。

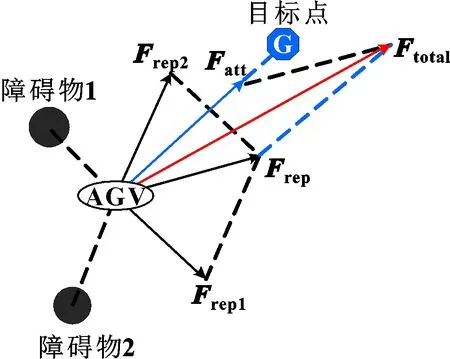
图1 传统人工势场法受力分析

2 改进人工势场法

2.1 障碍物处理

2.1.1 障碍物膨胀处理

传统人工势场法假定的行车环境是无限大的平面区域，忽视了实际行车环境中道路边界对路径规划的影响，因此适用范围有限。为便于实际路径规划，改进算法将道路边界障碍化，对包含道路边界在内的所有障碍物进行圆形膨胀处理。将全部障碍物切割成若干半径为的障碍圆，所切障碍圆相邻两者必相交(即两障碍圆圆心距离小于2)，要求障碍物影响范围大于障碍圆半径，且障碍物可全部被障碍圆覆盖。

如图2所示为模拟的实际行车环境，包含道路边界及若干形状大小各异的障碍物。图3是将实际行车环境中道路边界障碍化并且对包含道路边界在内的所有障碍物进行了膨胀处理之后的环境。

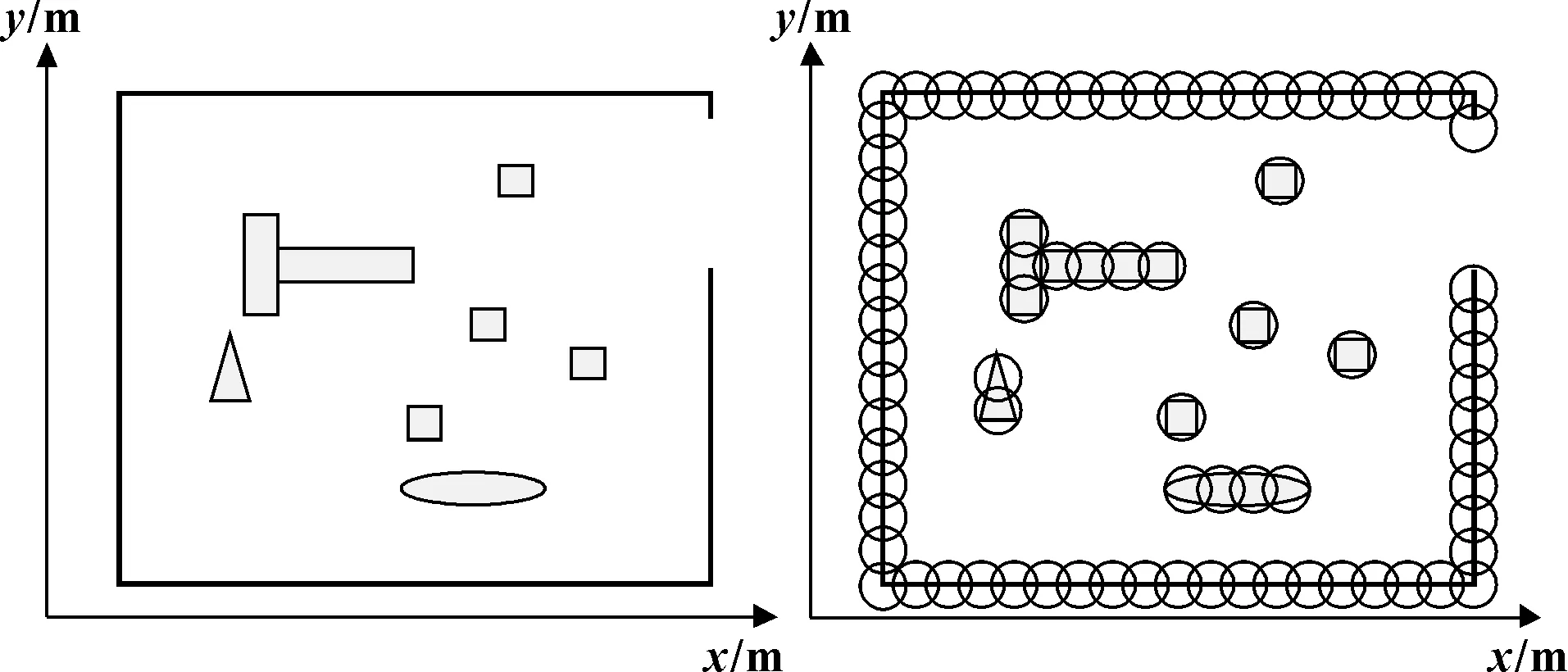
图2 实际道路边界及障碍物 图3 膨胀处理后道路边界及障碍物

2.1.2 障碍物陷阱优化

传统人工势场法对复杂障碍物环境的适应性差。在障碍物密集区域，AGV在多个障碍物共同作用下，极易掉进障碍物陷阱无法逃脱，从而导致路径规划失败。针对这一问题，采用障碍物连锁处理，将密集区域中距离较近的多个障碍物连锁起来，形成新的障碍物。具体连锁过程：设置阈值，搜索某一障碍物周围是否存在与它距离小于的其他障碍物，若存在，则将该障碍物与符合连锁条件的其他障碍物沿着障碍圆切线进行连接，用虚拟障碍圆填补连接空缺形成新的障碍物，如图4所示。

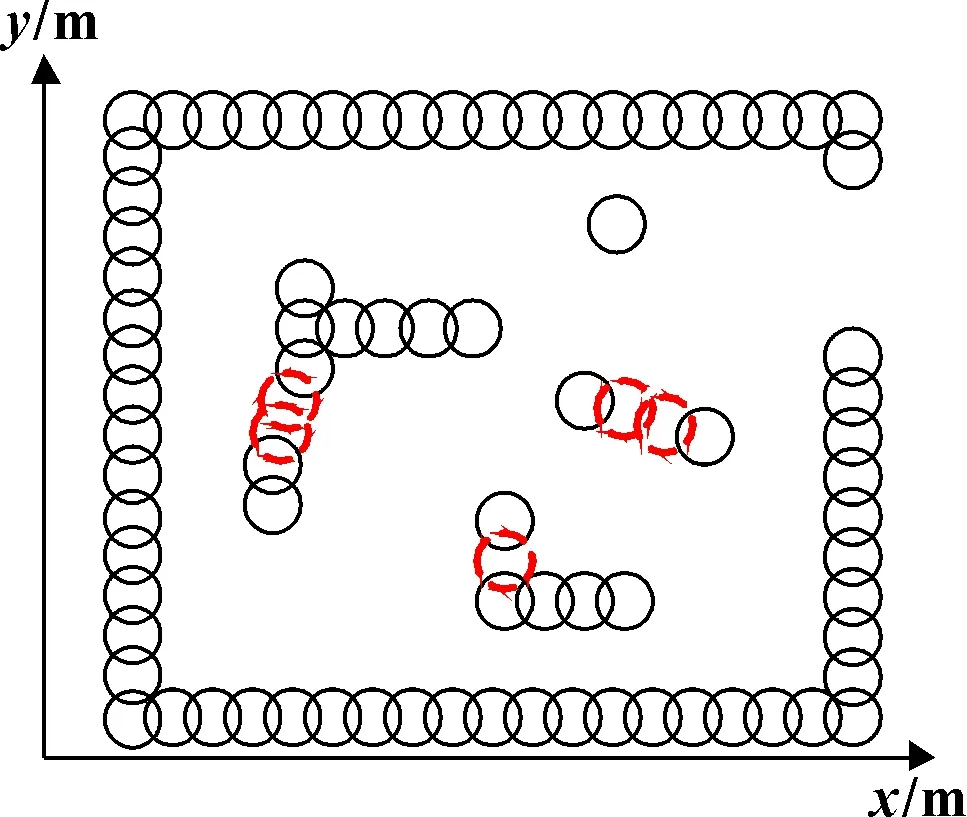
图4 连锁处理障碍物

2.2 改进势场斥力

采用传统人工势场法进行路径规划，当AGV到达目标点附近，目标点附近存在障碍物时，AGV在该处所受障碍物斥力远大于目标点引力，AGV将一直在目标点附近徘徊而无法到达目标点。针对传统人工势场法的目标不可达问题，在斥力势场函数中引入AGV与目标点间的距离因数。改进斥力势场受力分析如图5所示。

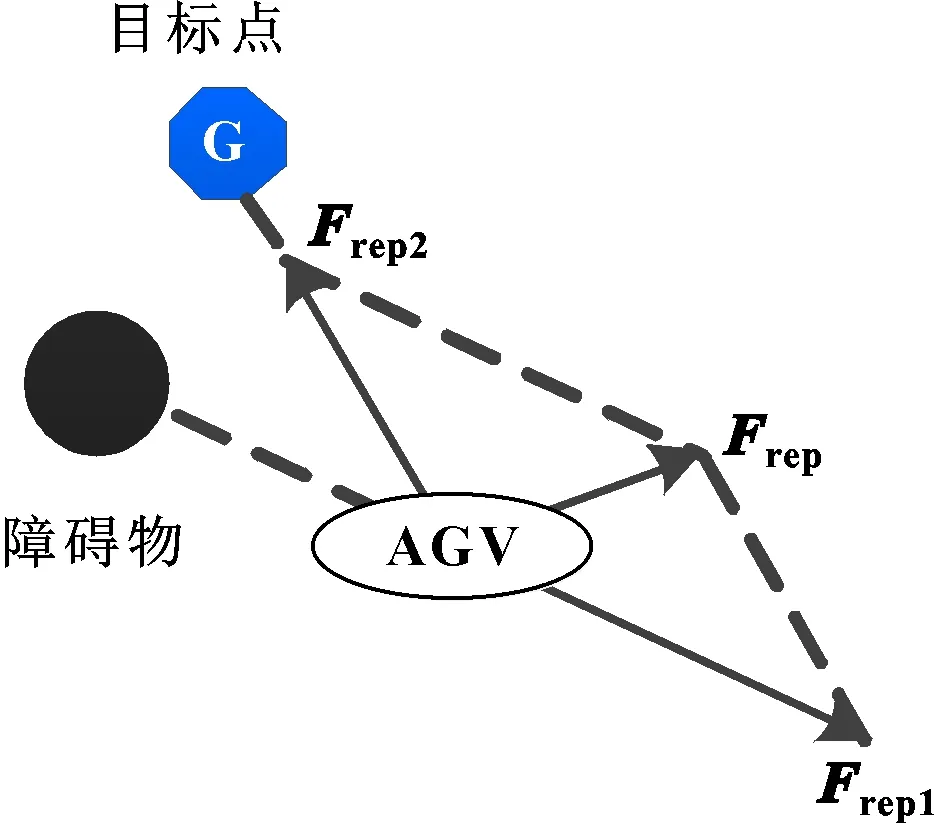
图5 改进斥力受力分析

改进后斥力势场函数如下：

=

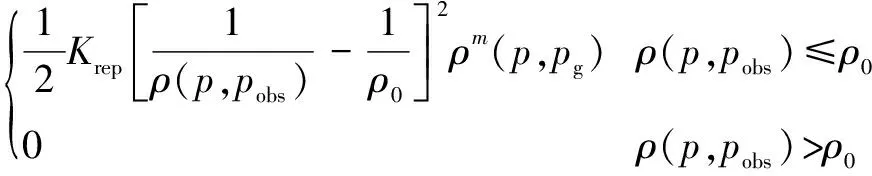
(5)

式中：为大于零的任意常数;其余参数含义同公式(1)(2)。

斥力势场函数求负梯度得到改进后的斥力函数如下：

(6)

式中：

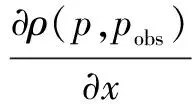
(7)

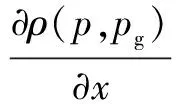
(8)

方向为障碍物指向AGV；方向为AGV指向目标点。

2.3 局部极小值问题优化

AGV在多个障碍物叠加的斥力场和引力场的共同作用下，极易达到力的平衡状态，此时AGV陷入局部极小值陷阱，在该处徘徊不前，导致AGV路径规划失败。

如图6和图7所示:当AGV到达所受障碍物斥力和目标点引力大小相同、方向相反的某个位置时，AGV陷入局部极小值点。

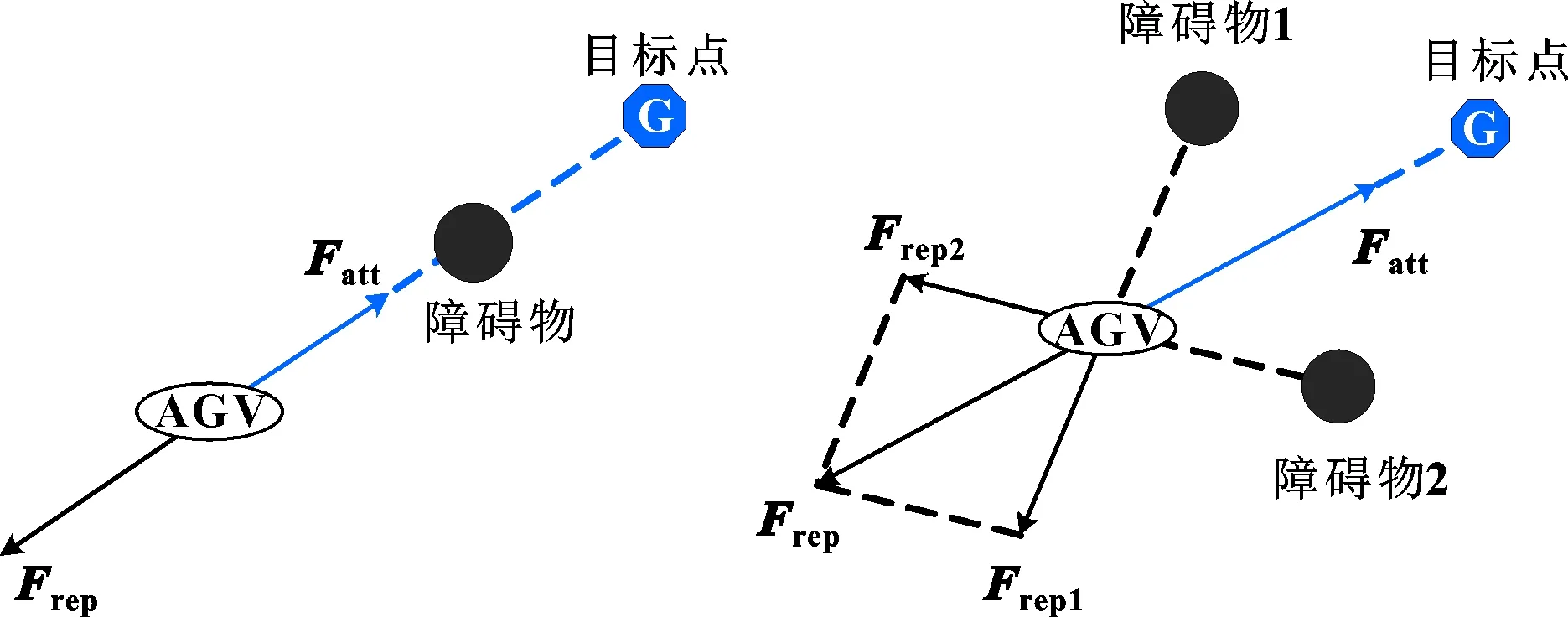
图6 单障碍物局部极小值问题 图7 多障碍物局部极小值问题

针对传统人工势场法路径规划中的局部极小值问题，采用增加虚拟障碍物的方法进行优化。针对图6所示的单障碍物局部极小值问题，当AGV、目标点、障碍物位于同一条直线时，如图8所示，求取障碍物当前位置坐标以及AGV位置坐标，障碍圆(障碍物膨胀处理所得)半径为，首先求取当前AGV在障碍圆上的切点，在AGV与障碍圆切点的连线上取距离(AGV最大几何尺寸)设置虚拟点。在虚拟点与当前AGV连线反方向距离(AGV最大几何尺寸与AGV与障碍物间安全余量之和)处产生虚拟障碍物点。

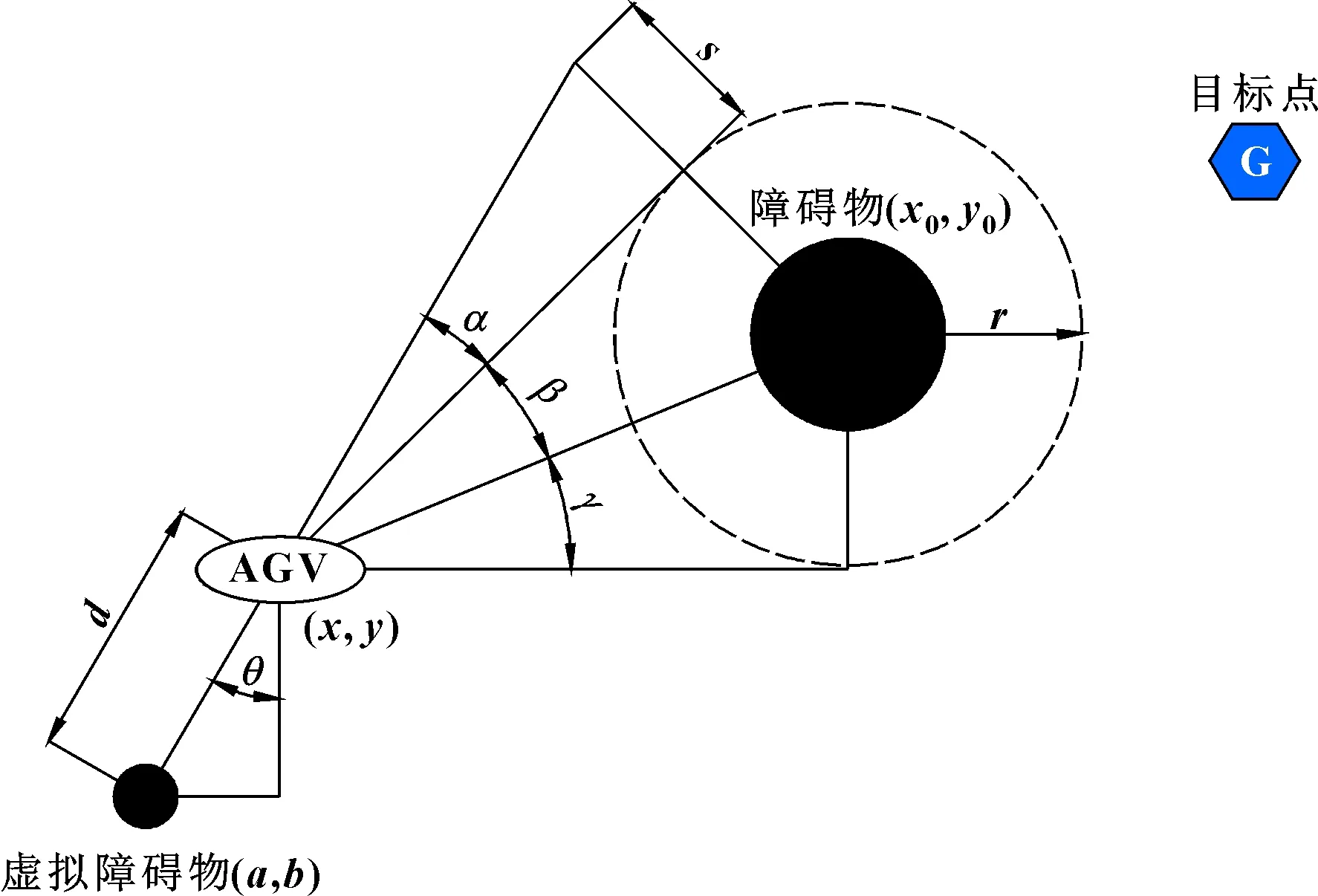
图8 单障碍物局部极小值改进

虚拟障碍物点建模方法如下：AGV当前坐标(,),障碍物坐标(,),虚拟障碍物坐标(,)，建立模型如下：

先求出AGV与障碍物间的距离：

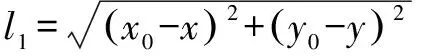
(9)

AGV与障碍圆切点距离：

(10)

分别求出3个夹角、、：

=arctan()

(11)

=arcsin()

(12)

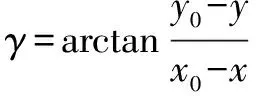
(13)

从而求得夹角:

=90°---

(14)

根据三角形余弦定理得出虚拟障碍物坐标：

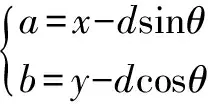
(15)

将公式(9)—(14)代入公式(15)得到虚拟障碍物位置坐标(,)：

=-(+)·

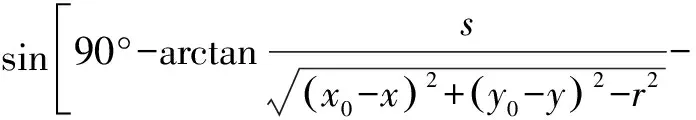
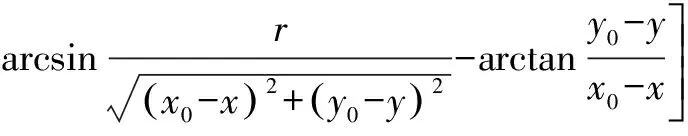
(16)

=-(+)·

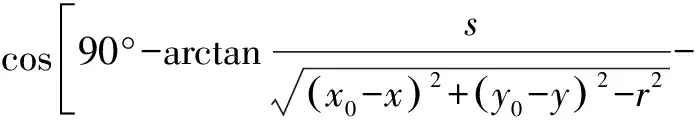
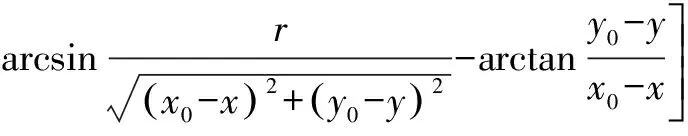
(17)

针对图7所示的多障碍物局部极小值问题，首先比较两相邻障碍物之间的距离与2+(为AGV最大几何尺寸，为AGV与障碍物间安全余量)的大小。若<2+，则虚拟障碍物的设置同上述单障碍物局部极小值问题；若>2+，则采用在目标点与当前AGV位置延长线设置虚拟障碍物的方法。如图9所示，在目标点与当前AGV位置延长线处设置虚拟障碍物点。具体建模方法如下：AGV当前坐标(,),目标点坐标(,),虚拟障碍物坐标(,)，建立模型如下：

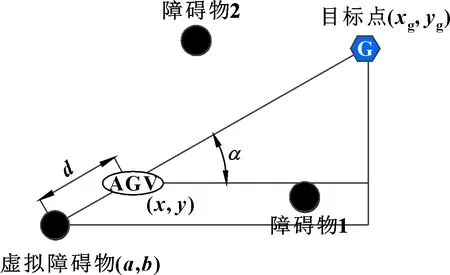
图9 多障碍物局部极小值改进

求出夹角：

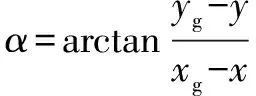
(18)

根据三角形余弦定理得出虚拟障碍物坐标：

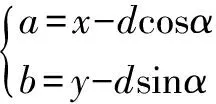
(19)

点(,)即为此时虚拟障碍物位置坐标点。

3 实验验证及结果分析

针对传统人工势场法存在的缺陷，提出了3个方面的改进，改进的人工势场法路径规划流程如图10所示。

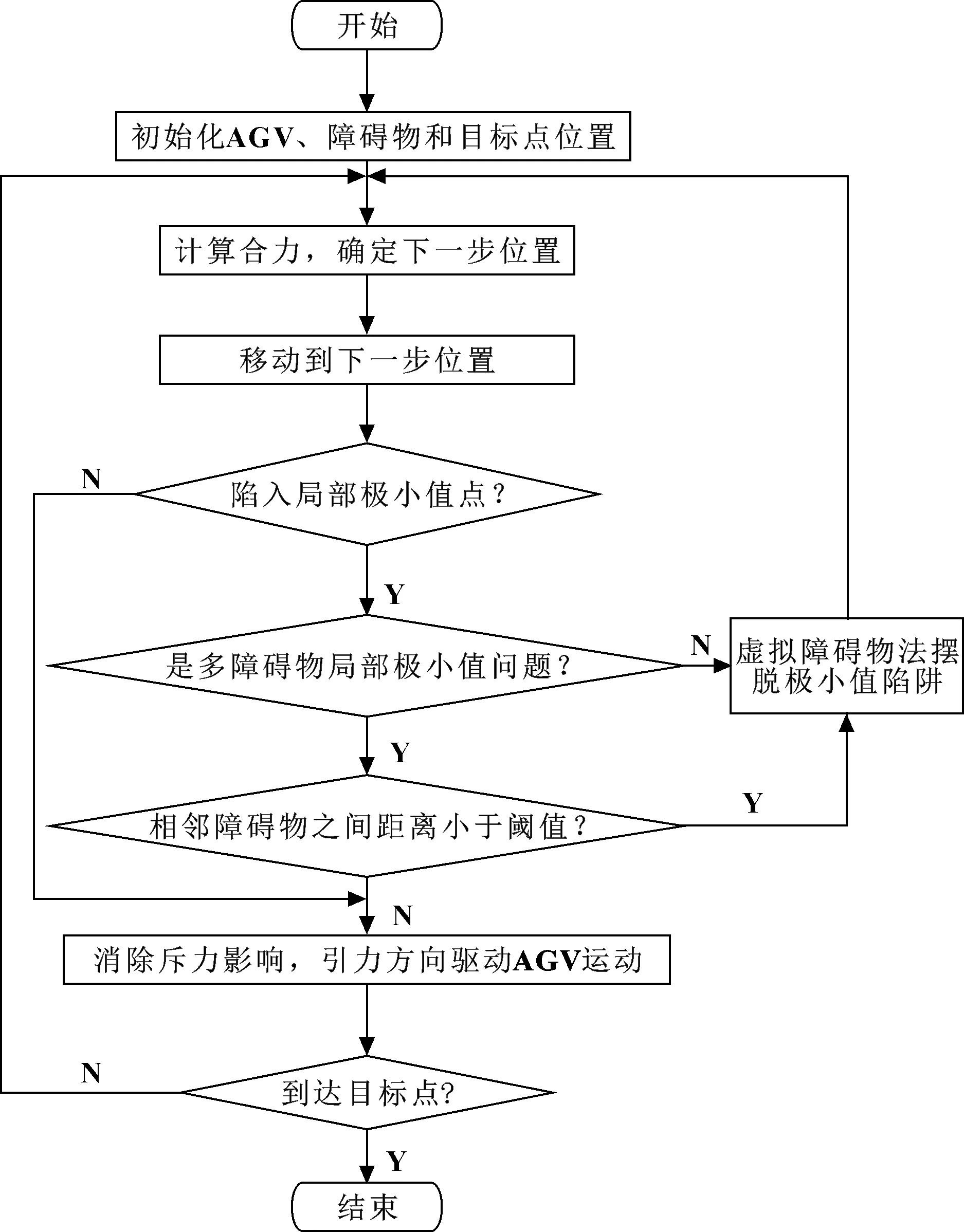
图10 改进人工势场法路径规划流程

为验证改进算法的有效性，对传统人工势场法和改进算法在MATLAB平台进行仿真分析。仿真环境为15×15的区域，路径规划的起点位置是(1，1)，目标点是(13，13)。其中黑色三角形表示散布在运动环境中的多处障碍物，左下侧红色五边形表示起始点，右上方蓝色五边形表示目标点，红色圆圈表示障碍物连锁过程中的虚拟填充障碍物，紫色三角形表示目标不可达实验中设置的虚拟障碍物。

实验验证分为三部分：障碍物陷阱问题验证、目标不可达问题验证以及局部极小值问题验证。改进算法有效性的评价标准是：在障碍物密集区域，通过障碍物连锁处理能够使AGV逃离障碍物陷阱并且实现路径优化；目标点附近存在障碍物时，使用改进算法后AGV可以成功到达目标点位置；AGV陷入局部极小值陷阱时，利用改进算法能够成功逃脱极小值陷阱，最终到达目标点。实验中2种算法参数设置如表1所示。

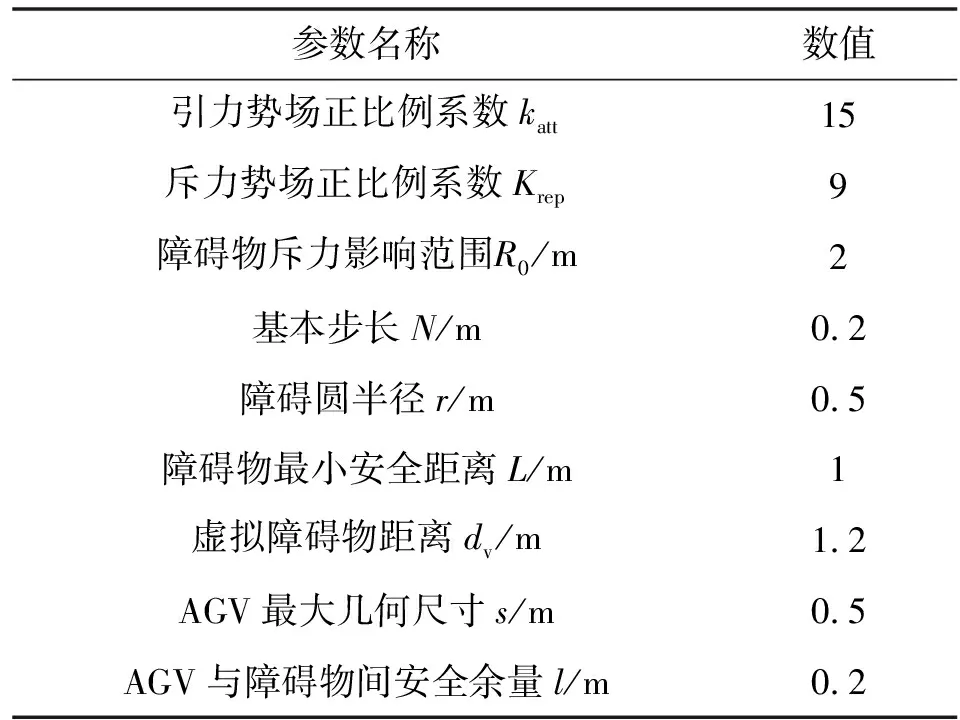
表1 实验参数名称及数值

图11和图12所示为存在多处障碍物陷阱时的实验分析对比。由图11可知：在利用传统人工势场法进行路径规划时，受障碍物群影响，规划出的路径相对冗长。且在障碍物密集区域，AGV掉进障碍物陷阱无法前进，导致路径规划失败。图12中，在利用改进算法进行路径规划时，对障碍物密集区域符合连锁条件的障碍物进行连锁处理后，AGV能够成功避开障碍物陷阱，并且规划出来的路径相对缩短。

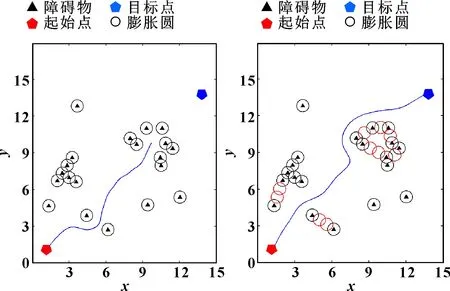
图11 传统障碍物陷阱路径规划 图12 改进障碍物陷阱路径规划

图13和图14所示是目标不可达实验分析对比，在目标点(13，13)附近(13.2，13.2)处设置障碍物。图13所示为使用传统人工势场法进行的路径规划，AGV在目标点附近由于斥力远远大于引力，AGV陷入目标不可达陷阱，无法到达目标点。图14所示为使用改进算法进行的路径规划，对传统算法斥力函数进行改进后，AGV能够成功到达目标点，完成了从起始点到目标点的路径规划。

图13 传统目标不可达路径规划 图14 改进目标不可达路径规划

图15和图16所示是局部极小值实验分析对比。图15所示是存在多处局部极小值问题的传统算法路径规划，当AGV到达点时，所受障碍物斥力和目标点引力大小相同、方向相反，AGV出现徘徊不前等状况，导致路径规划失败。采用改进算法后，如图16所示，当AGV陷入局部极小值时，在点附近合适位置设置虚拟障碍物，使AGV在处所受合力不为0，成功跳出局部极小值陷阱。到达处，AGV再次陷入局部极小值点，根据算法判定两障碍物距离大于预设最小值，因此在目标点与点连线延长线合适位置设置虚拟障碍物，使AGV跳出局部极小值点，成功到达目标点。

图15 传统局部极小值路径规划 图16 改进局部极小值路径规划

综上，使用传统人工势场法容易掉进障碍物陷阱以及局部极小值陷阱，当目标点附近存在障碍物时，容易出现目标不可达问题。使用改进算法，成功解决传统人工势场法存在的缺陷，规划出一条从起始点到目标点的无碰撞路径。

4 结论

对传统人工势场法存在的问题进行分析，通过将道路边界障碍化，障碍物密集区域采用障碍物连锁处理，改善了实际环境适应性差的问题；针对目标不可达问题，引入目标点与AGV间的距离因数，使AGV接近目标点时，斥力逐渐减小到零，解决了目标不可达问题；针对实际规划中的局部极小值问题，采用引入虚拟障碍物的方法，使AGV在到达目标点途中能够跳出合力为零的局部极小值点，顺利到达目标点。最后通过实验对改进算法进行了验证，实验结果表明：改进算法可以使AGV成功避开障碍物陷阱，规划出一条从起始点到目标点的无碰撞路径。