基于分形理论的粗糙齿面齿轮动力学研究

2022-09-21谢磊李政民卿

机床与液压 2022年17期

谢磊，李政民卿

(南京航空航天大学，直升机传动技术国家级重点实验室，江苏南京 210016)

0 前言

齿轮传动具有传动精确、平稳、高效以及结构紧凑和承载能力大等优点，被广泛应用于汽车、船舶和航空等领域。近年来，齿轮动力学仍是齿轮相关领域的研究热点，许多国内外学者针对齿轮的动力学特性，考虑时变啮合刚度、误差、齿侧间隙和齿面摩擦等因素,展开了大量研究并取得了丰硕的研究成果，为进一步深入研究齿轮动力学奠定了良好基础。

在考虑误差的齿轮动力学研究中，BONORI和PELLICANO建立了包含随机加工误差的齿轮动力学模型，分析了随机分布齿廓误差对动力学的影响；INALPOLAT等研究了以周节误差引起的长周期准静态传递误差为主要激励的齿轮动力学特性；WANG和ZHANG将传递误差分解为谐波分量与随机分量，提出了考虑随机误差的齿轮系统动态分析模型；常乐浩等研究了齿轮综合啮合误差的计算方法及它对系统振动的影响；石照耀等提出了齿轮副整体误差的概念与获取方法，研究了考虑整体误差的齿轮动力学行为；黄康等人基于分形理论研究了粗糙度影响下的齿轮非线性动力学行为，但模型为简化较多的纯扭转模型。现有研究表明，齿面微观形貌会对误差产生较大影响，但现有齿轮动力学研究中常因粗糙齿面的复杂性而忽略其影响，且在研究时多未考虑摩擦这一重要因素，研究尚不全面。

针对上述问题，为剖析粗糙齿面对齿轮动力学的作用机制，进一步探究粗糙齿面对系统动态特性的影响，从而为工程齿面精度设计提供参考，本文作者利用分形理论对粗糙齿面进行分形表征，结合齿面摩擦因素，建立考虑粗糙齿面影响的齿轮多自由度非线性动力学模型，研究齿面粗糙度、齿面摩擦及工况对系统动力学特性的影响。

1 粗糙表面的分形表征

在齿轮的加工制造中，由于存在加工方法不同及刀具颤振等原因，实际加工齿面在微观上都是凹凸不平的，即存在一定的表面粗糙度。表1所示为不同加工方法下的齿面粗糙度范围，研究粗糙齿面对齿轮动力学特性的影响具有重要的实际意义。分形理论源自对海岸线形状的研究，它是解决非线性几何问题的常见方法。现实生活中，海岸线和粗糙表面轮廓线都是典型的分形曲线，粗糙表面的分形表征是分形理论在工程机械中的重要应用，因此文中采用分形理论模拟随机粗糙齿面。

表1 不同加工方法下的齿面粗糙度

目前，分形理论表征粗糙表面的方法主要有W-M函数模拟法、分形插值模拟法和时间序列模拟法等。W-M函数是处处连续而处处不可导且具有自仿射特征的分形曲线，在实际工程和科学研究领域中均得到了广泛应用。W-M函数构造式为

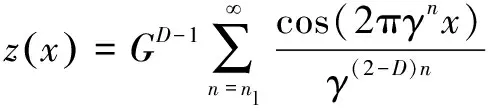
(1)

式中:为粗糙表面轮廓高度；为自仿射分形维数，它描述函数在所有尺度上的不规则性，对于二维分形，1<<2；为特征尺度系数，它决定粗糙轮廓的具体高度；为大于1的常数，一般认为齿面波纹度、粗糙度近似满足正态分布，故取1.5；为表面轮廓的截断频率;为最低截断频率。

轮廓算术平均偏差是最早被提出来的粗糙度评定参数，目前在国际上仍被多数国家采用。葛世荣、陈奇等人基于实验测定，分别给出了粗糙度关于分形维数和特征尺度系数的推荐关系式：

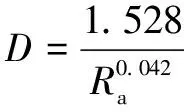
(2)

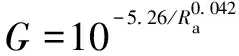
(3)

由此即可通过二维W-M分形函数生成不同表面粗糙度下的轮廓高度。图1所示为分别为0.4、1.6和6.3 μm时粗糙表面的模拟结果。

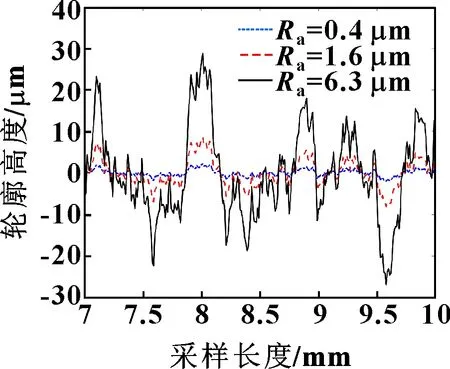
图1 不同表面粗糙度下的轮廓高度

2 齿轮动力学建模

2.1 直齿轮副啮合传动过程

图2所示为一对直齿轮副的啮合传动过程，由于直齿轮传动的重合度一般在1～2之间，故存在单双齿交替啮合情况。主动轮受驱动扭矩的作用以角速度带动从动轮旋转，从动轮的角速度及所受扭矩分别为和。图中为理论啮合线，为实际啮合线。齿对1在点啮入时齿对2在单齿啮合区下界点处啮合，随着齿轮转动，齿对2在点退出啮合，此时齿对1刚好到达单齿啮合区上界点，然后经过节点直至点，同时新一对的轮齿又从点啮入。在双齿啮合区，主动轮受一对动态啮合力、(LOA方向)和摩擦力、(OLOA方向)作用，和分别为齿对1和齿对2的摩擦力臂。

图2 直齿轮副啮合过程

2.2 动力学模型

利用集中参数法，建立如图3所示的齿轮动力学模型。以图示方向建立笛卡尔坐标系，每个齿轮均有和方向的平移自由度及绕轴旋转的扭转自由度。图中、分别为等效支撑刚度和支撑阻尼；、分别为啮合刚度和啮合阻尼；为静态传递误差；、、、分别为主从动轮的质量与转动惯量。为简化研究，假定主、从动轮的等效支撑刚度和阻尼均相同。由于滑动摩擦较滚动摩擦大很多，仅考虑齿间滑动摩擦。由于侧隙多在空载和轻载工况下影响较大，且侧隙引起的轮齿脱啮会导致齿面不存在摩擦作用，不考虑侧隙影响。

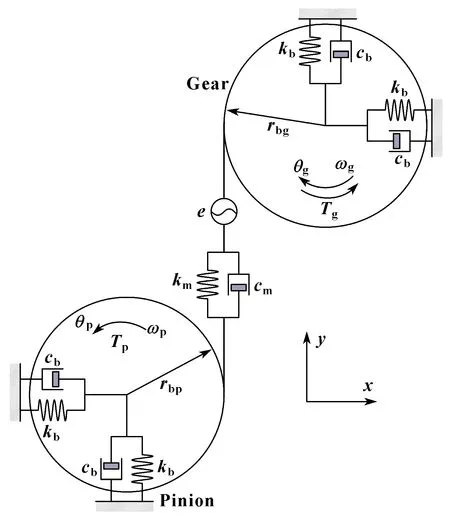
图3 动力学模型

鉴于粗糙表面接触的复杂性，假设两齿面接触时一齿面为粗糙表面而另一齿面光滑，且不考虑其他误差因素影响，仅以粗糙轮廓高度作为静态传递误差，以此研究粗糙齿面对齿轮动力学特性影响。

定义主、从动轮沿啮合线上的相对位移为动态传递误差与静态传递误差的差值：

=-=-+--

(4)

作用在第(=1,2)对轮齿的动态啮合力可表示为弹性啮合力与黏性啮合力之和：

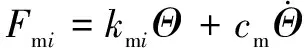
(5)

式中：m为第对轮齿的啮合刚度，文中采用应用十分广泛的石川公式求解啮合刚度，详细公式此处不再赘述，啮合刚度计算结果如图4所示；为啮合阻尼，可由如下经验公式表示：

图4 时变啮合刚度

(6)

其中：为啮合阻尼比；为齿轮副的等效质量；为平均啮合刚度。

定义为第对齿轮时刻在啮合线上的位移：

=mod(,)+(-1)

(7)

依据齿轮啮合几何原理，第对轮齿上的摩擦力臂可由下式求得：

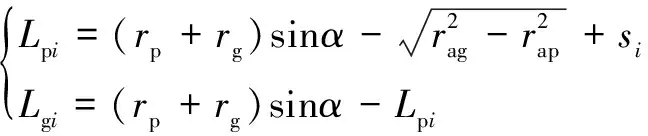
(8)

式中：、和、分别为主从动轮的节圆半径和齿顶圆半径。

主、从动轮第对轮齿所受的摩擦力分别为

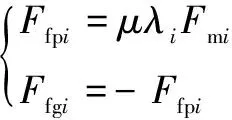
(9)

式中：为摩擦因数；为摩擦力换向系数，当相对滑动速度为正时取“+1”，为负时取“-1”，在节点处为“0”，可借助符号函数将其表示为

=sign(g-p)

(10)

则摩擦力矩可表示为

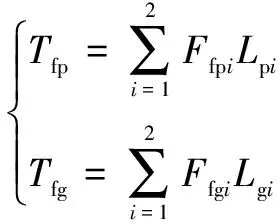
(11)

根据牛顿第二定律，系统的动力学微分方程为

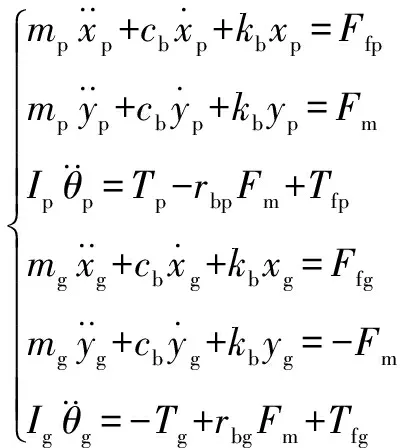
(12)

3 粗糙度对齿轮动力学特性的影响

齿轮传动系统是极其复杂的非线性时变系统，其动力学方程一般难以获得解析解，因此数值仿真是分析齿轮动力学问题的常用方法。此节选取一组齿轮基本参数，如表2所示，利用Simulink仿真器和内置的定步长Runge-Kutta法对动力学方程进行数值求解，研究相关参数对动力学特性的影响。

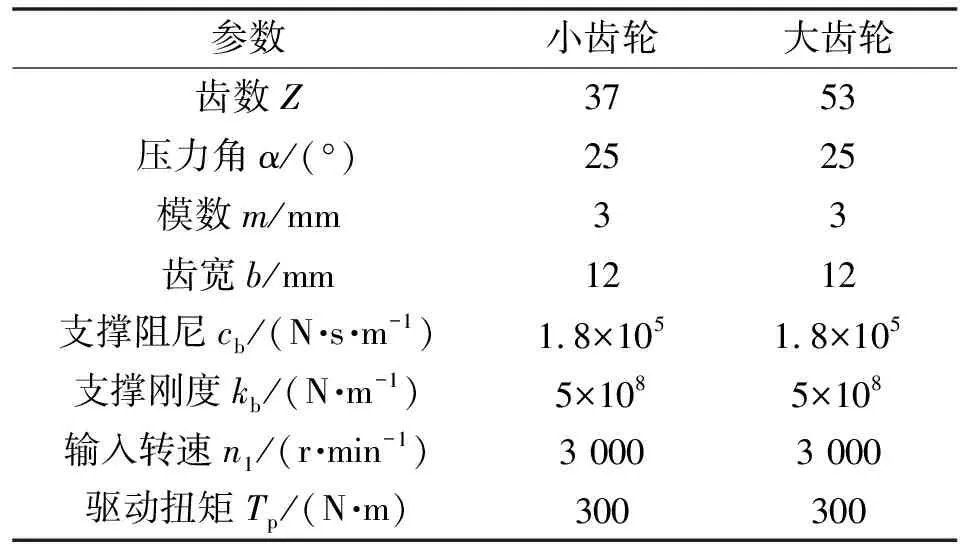
表2 齿轮基本参数

3.1 齿面粗糙度对动力学特性的影响

齿轮传动过程产生的动态传递误差是反映系统振动特性的关键因素，图5为粗糙度分别为0.4、1.6、6.3 μm时动态传递误差的时域谱、频域谱和相图。由图5(a)可知：啮合轮齿存在明显周期性冲击，当粗糙度由0.4 μm上升至6.3 μm时，动态传递误差显著增大，经计算其方均根值由23.49 μm上升至24.63 μm；由图5(b)可知：频率成分主要为啮合频率及其倍频，粗糙度主要影响动态传递误差的二阶振动分量，对其他频段影响较小；由图5(c)可知：相图为一不规则封闭曲线，表明系统为单周期非简谐振动且随着粗糙度上升，系统的周期运动更加复杂，振动愈发不稳定，动态性能逐步恶化。

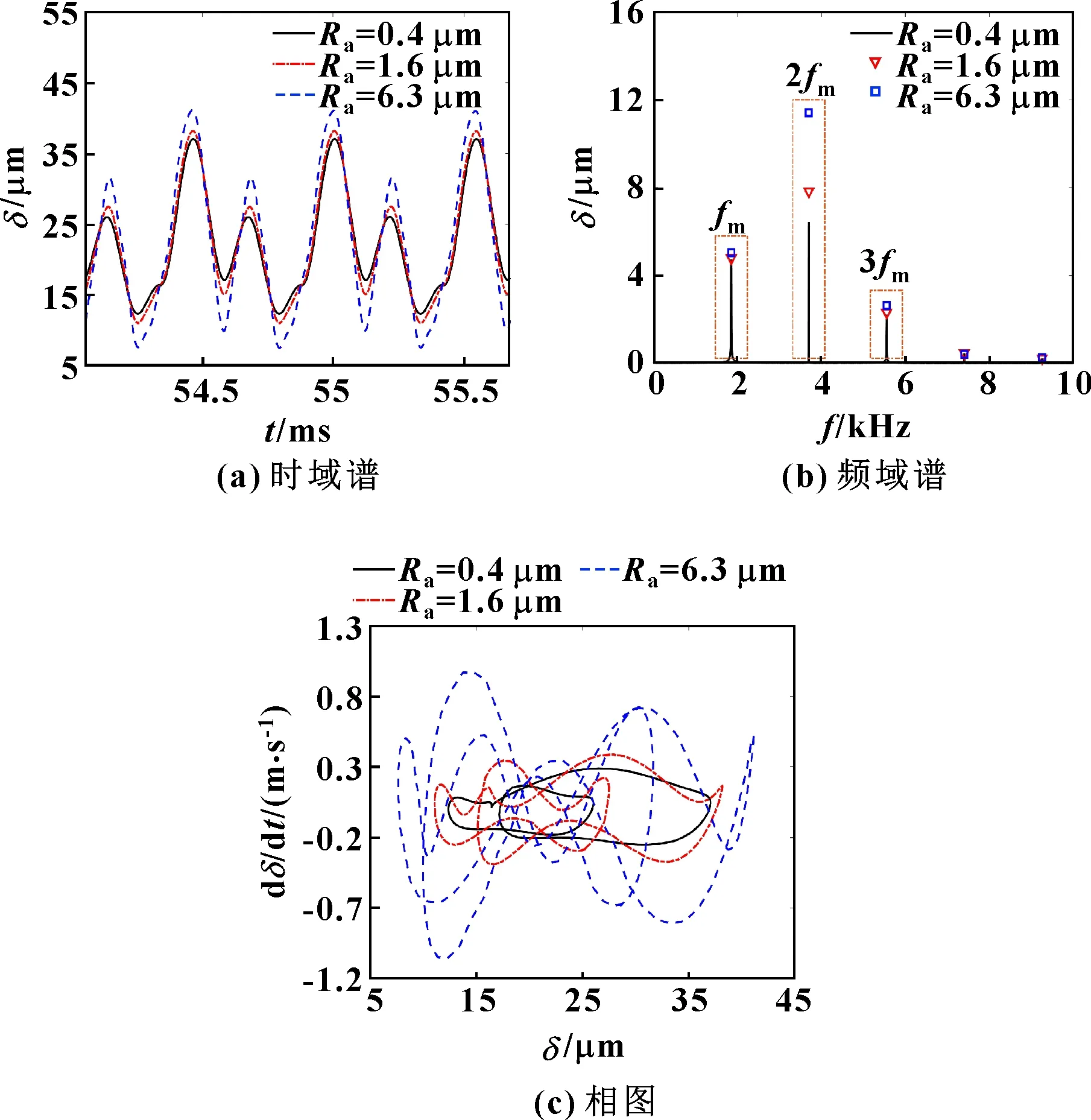
图5 不同粗糙度下动态传递误差

3.2 齿面摩擦对动力学特性的影响

当齿轮传动处于不同的润滑状态或齿面出现损伤时，齿面摩擦因数变化较大，目前仍无可准确描述粗糙度与摩擦因数关系的解析式。此节以摩擦因数为0、0.05、0.2来表示不考虑摩擦、正常润滑及损伤乏油工况，齿面摩擦对系统动力学特性的影响。图6—图8分别为小齿轮沿和方向的振动位移以及齿轮副动态传递误差的时频域响应。

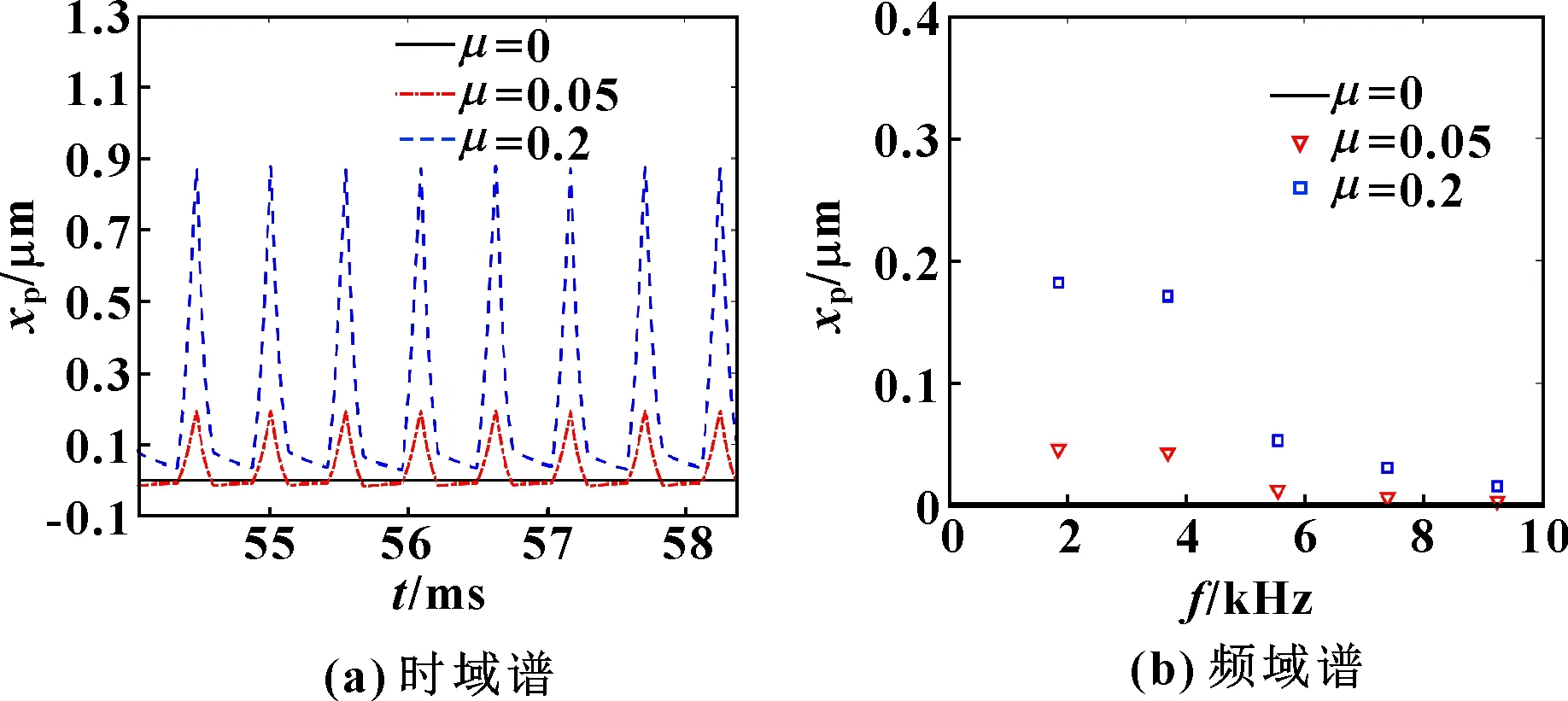
图6 小齿轮x向振动位移

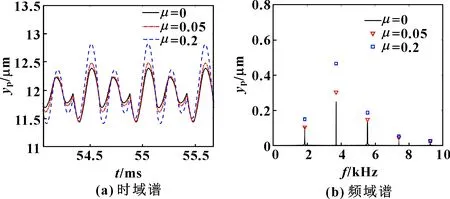
图7 小齿轮y向振动位移

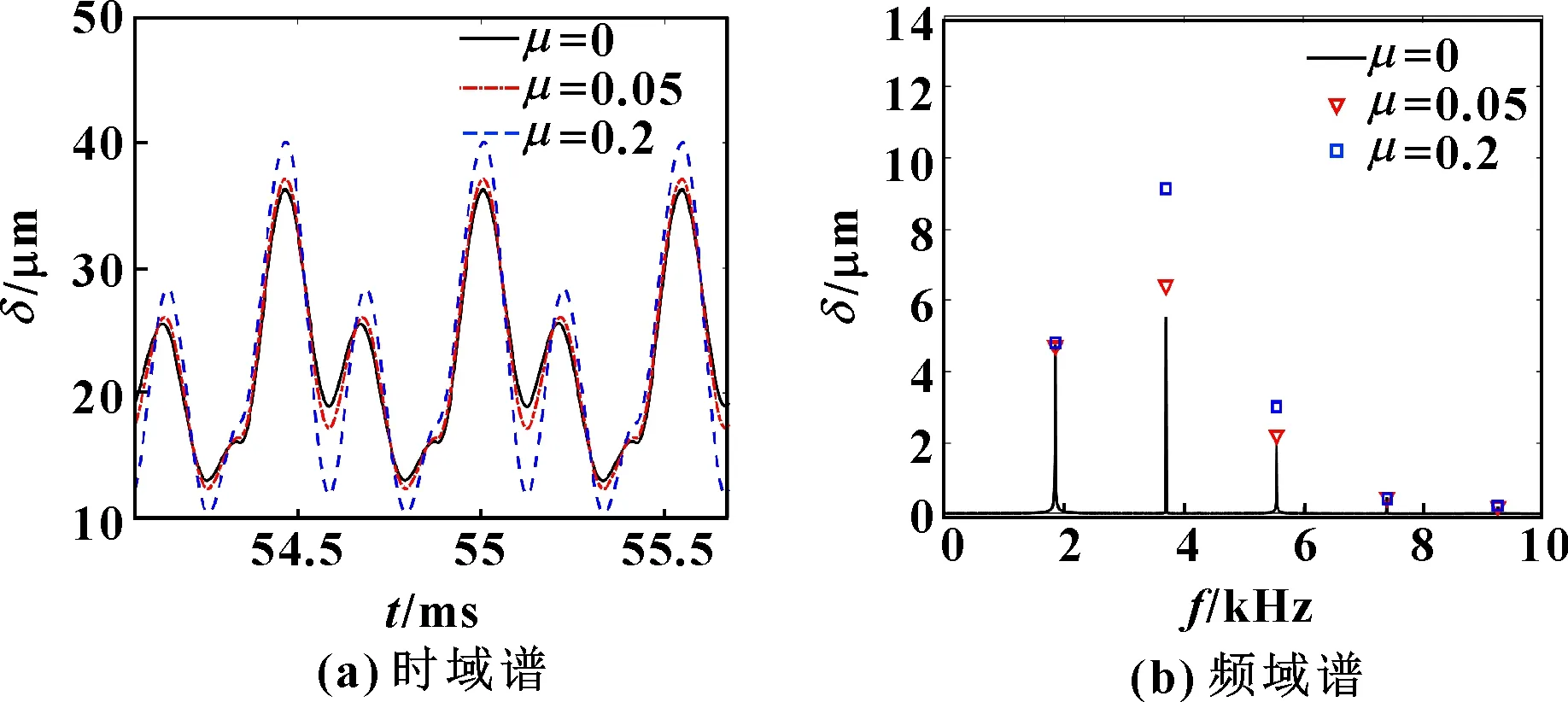
图8 不同摩擦因数下动态传递误差

由图6—图8可知：摩擦因数上升使得小齿轮沿和方向的振动位移以及系统的动态传递误差均增大，表明齿面摩擦会导致系统的振动和噪声加剧，这与文献[15]的结论一致。此外，由于齿面摩擦作用于垂直啮合线方向，它是导致方向振动的主要激励，因而对该方向的振动影响更显著。由图6—图8所示的频域谱可知：齿面摩擦主要影响系统振动位移的前3阶振动分量，对高频振动分量的影响较小。

3.3 工况对动力学特性的影响

在实际应用中，齿轮传动机构常工作于不同工况下，且现代工业正朝着高速、重载的方向发展，研究变工况下粗糙度对齿轮动力学特性的影响，对齿轮传动系统的设计及应用均具有重要意义。图9所示为低速轻载、高速轻载和高速重载3种工况下粗糙度为0.4、1.6、6.3 μm时系统的动态传递误差响应，对应的各工况参数如表3所示。

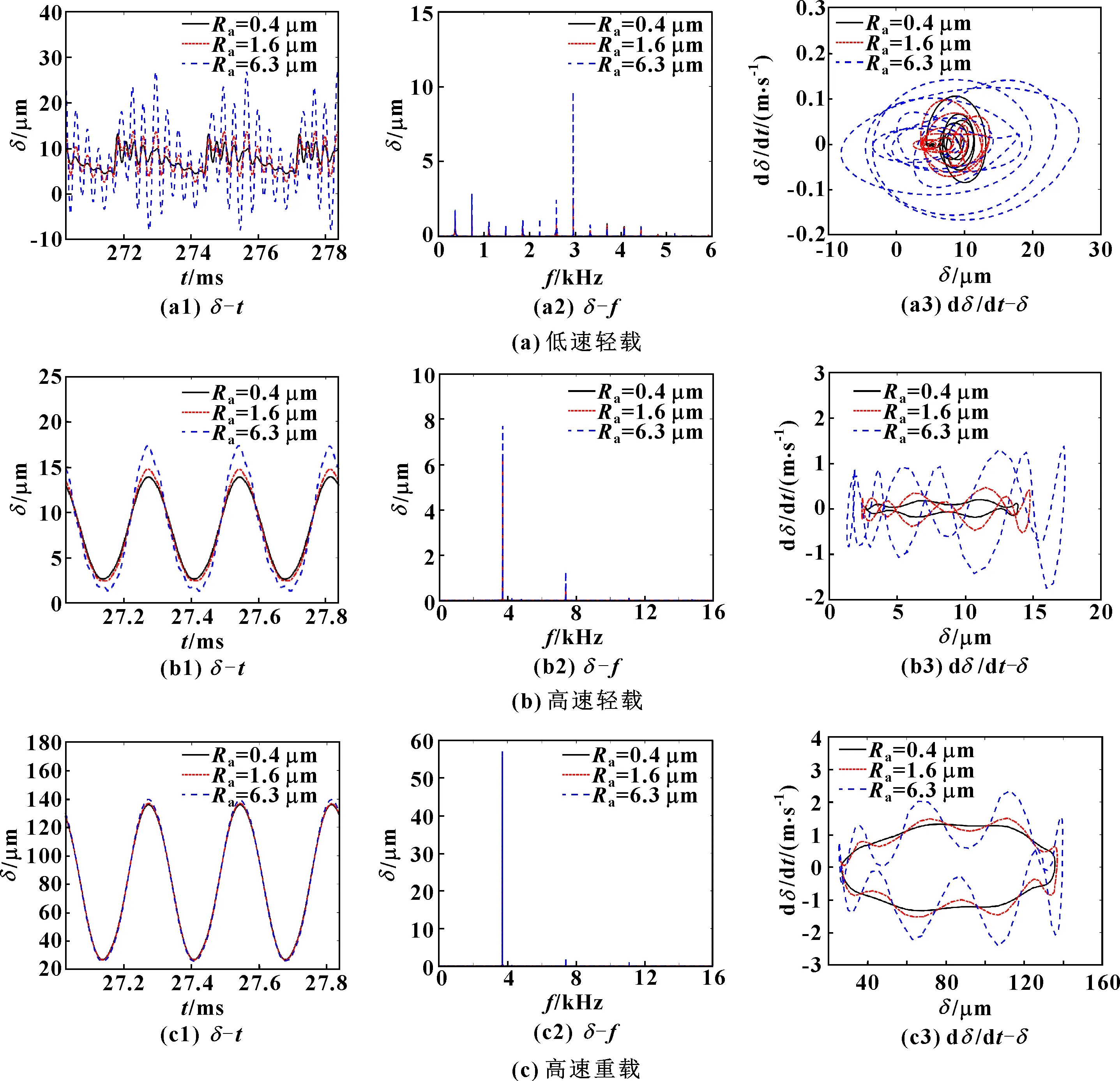
图9 不同工况下动态传递误差

表3 工况参数

由图9可以看出：在低速轻载工况下，动态传递误差的振动规律、频率成分和相轨迹较为复杂，粗糙度上升后，动态传递误差显著增大，相轨迹愈发复杂，系统的振动特性逐渐变差；随着工况由低速轻载向高速重载变化，动态传递误差的冲击明显降低，频率成分逐渐减少，相轨迹愈发趋于规则封闭曲线，系统的振动稳定性提高；在高速重载工况下，粗糙度增大对系统动态传递误差的时频域响应及相图的影响较低速轻载时显著减小。这表明当转速和扭矩增大时，齿轮传动的啮合时间减小，法向载荷增大，使得齿轮副的接触周期与状态发生明显变化，进而导致粗糙度对动态特性的影响越来越小。上述研究表明，粗糙度对齿轮动力学特性的影响因工况变化而不同，结合工况合理地进行齿面精度设计，有利于进一步平衡加工成本与传动质量之间的关系，降低齿轮传动的振动和噪声。