基于Triplet loss的电磁阀故障识别方法

张文啸， 孟国香， 叶 骞

(1.上海交通大学机械与动力工程学院， 上海 200240；2.中国科学院上海天文台射电天文科学与技术研究室， 上海 200030)

引言

随着工业化水平不断进步，人们对自动控制系统的需求也在不断增大。在所有自动控制系统中，以流体作为介质的电气、电液控制占据了很大比例，而电磁阀作为电气、电液控制系统中重要的执行器，也受到了业内学者的广泛研究。

经过几十年的发展，电磁阀以其成本较低、结构简单、工作状态较稳定、退化周期较长等优点被广泛应用于电网设备、车辆船舶、医疗器械等自动控制领域。正因为电磁阀在越来越多的控制系统中成为关键甚至核心部件，其故障的检出、诊断和处理成为学者们重点研究议题。随着众多研究的不断深入和工业领域内自动化程度的不断提高，对于电磁阀的故障诊断也逐渐由依赖于简单的测量仪器和专家知识的经验性诊断，转向了基于精密传感器和计算机的智能诊断。范超[1]、项超鹏[2]提出通过采集电磁阀驱动端电流，并提取了小波包变换后的各层小波包系数作为特征向量，用BP神经网络构建故障检测模型的诊断方法。谭洋波等[3]通过对电磁阀工作电流信号进行EMD分解，建立了决策树判别模型，诊断准确率达到98%以上。

彭军等[4]通过采集电磁阀驱动端电流并提取启动电流的响应时间、稳定时间、局部最大值、局部最大值积分等特征，组成特征向量并输入多层感知机进行训练，得到具有较高识别率的故障诊断模型。

以上智能诊断方法虽然均对于电磁阀有较好的诊断效果，但诊断模型的建立都需要首先对采集得到的信号进行特征提取，这就要求使用者需要具有一定的先验知识。此外，不同的特征提取方式可能对模型的识别效果有不同的影响，对于不同型号、类型的电磁阀，最佳的特征提取方式也会有所不同。这些因素都限制了上述方法的普适性。

针对这个问题，近年来在工业设备领域，关于“端对端”故障诊断的研究逐渐增多。尹爱军等[5]对滚动轴承的振动信号进行FFT变换后，输入变分自动编码器，建立了无需手动提取特征的轴承健康状态评估模型。张祥等[6]针对TE过程数据集，构建了基于变分自动编码器-深度置信网络(VAE-DBN)的端对端故障诊断模型。据这些工作的启发，本研究首先提出了一种基于变分自动编码器(VAE)的端对端电磁阀故障诊断模型，并利用三元组损失(Triplets loss)对模型进行了改进，使得模型对不同工作频率下的电磁阀具有更好的故障诊断泛化能力。

1 数据采集与预处理

1.1 对象电磁阀结构

电磁阀的种类较多，最常见的分类方式之一是按照工作原理，将电磁阀分为直动式、先导式以及分步直动式。其中，先导式电磁阀的工作原理可以简要描述为：通电后电磁力作用使阀杆提起，导阀口打开，从而使电磁阀上腔通过先导孔泄压，在主阀芯前后形成压力差，依靠此压力差来推动主阀芯，使主阀口打开；断电后，在弹簧力作用下，阀杆复位，先导孔关闭，主阀芯向下移动从而使主阀口关闭，电磁阀上腔压力重新升高，流体压力施加在主阀芯上，从而使密封效果更好。

本研究的对象为某公司的二位五通先导式电磁阀，其外观如图1所示，图2为其原理图。

图1 二位五通先导阀外观Fig.1 Appearance of 5/2-way pilot valve

1.2 数据采集系统

为了研究基于数据驱动的电磁阀故障诊断模型，首先需要对电磁阀的常见故障进行分析，并采集相应的数据。电磁阀的常见故障主要有不能关闭、响应迟缓、流量小和有异响[7]。其中不能关闭是最为严重的故障，常常会导致整个控制系统完全失效，产生难以估量的经济损失。因此，基于故障易发程度和人为模拟难易程度，选择故障表现为“不能关闭”下的“阀芯被异物卡塞”和“密封件损坏”两种故障原因，进行故障模拟和数据采集，如表1所示[7]。

表1 模拟电磁阀故障工况选择Tab.1 Simulation of valve failure condition

对于“阀芯被异物卡塞”工况，模拟方式如图3所示，拆开阀体和端板后，在阀芯端部与端板的空隙处放置大小合适的铝制金属块，而后再将阀体和端板重新装配。

图3 阀芯卡塞工况模拟方式Fig.3 Simulation method of stuck condition

对于“密封件损坏”工况，模拟方式如图4所示，拆卸开阀体和底板后，将其中的密封垫取出，而后再将阀体和底板重新装配。

图4 密封件损坏工况模拟方式Fig.4 Simulation method of seal failure condition

在信号选取上，除前述研究中多用到的驱动端电流信号外，还增加了2个通道的信号，分别是阀前进气口处的气压信号和线圈附近的磁场强度信号。前者使用压力变送器，将气压值转换为0～5 V电压值进行输出；后者使用线性霍尔元件，将磁场强度转换为0～5 V 电压值进行输出。将驱动端电流、进气口气压、磁场强度这3路信号均转换为0～5 V电压值后，再通过数模转换电路ADS1115转换为数字量，用树莓派进行采集。图5是本研究所用到的数据采集台。

1.电磁阀 2.数模转换芯片 3.气路负载(气爪) 4.继电器5.树莓派 6.220V-24V电源 7.压力变送器图5 数据采集台Fig.5 Data collection test bench

分别在3种工况下采集数据，3种工况分别为：正常(电磁阀健康)工况、阀芯卡塞工况和密封件损坏工况。为了后续章节所构建的模型有更好的泛化能力，对每种工况又分别在工作气压为0.1， 0.2， 0.3 MPa下，工作频率在0.5， 1， 2 Hz下采集数据，对每种工况的数据采集量如表2所示，即每种工况共采集18 h数据，3种工况合计54 h数据。受限于ADS1115的性能，多通道同时采集时，采样频率设置为16 Hz，在电磁阀的工作频率不超过2 Hz的情况下可以确保信号不失真。

表2 单一工况数据采集量Tab.2 Amount of data collected in a single working condition

1.3 数据预处理及数据集生成

在采集完数据后，还需要对数据进行预处理，以及整理为数据集，以便于后续章节诊断模型的建立。如图6a为进行预处理前的三通道信号，单位为V。可以看出，受限于传感器质量，在采集过程中不可避免的有一些异常值。采用IQR准则[8]剔除异常值，处理后的数据如图6b所示。

图6 去除异常值前后信号对比Fig.6 Comparison of signals before and after outlier removal

接着需要将全部数据整理成带标签的数据集。为了验证后续章节提出的故障诊断模型对处于不同工作频率的电磁阀的故障检测的泛化能力，训练集和测试集涵盖不同的工作频率的数据。具体而言，训练集中包含健康、阀芯卡塞、密封件损坏3种工况，但仅选取了0.5 Hz和2 Hz工作频率下的数据；测试集中包含健康、阀芯卡塞、密封件损坏3种工况，选取了0.5， 1， 2 Hz工作频率下的数据。

在数据的切分上，以20 s为长度，将数据切分为片段样本。由于采样频率为16 Hz，则每个样本有3个通道，长度为320。在标签的设置上，将健康、阀芯卡塞、密封件损坏3种工况的标签分别设置为0，1和2。数据集全部整理完毕后得到的训练集大小为(5018，320，3)，测试集大小为(5099，320，3)。

2 基于变分自动编码器的电磁阀故障诊断模型

2.1 变分自动编码器

变分自动编码器(Variational Auto Encoder，VAE)是一种生成模型，从传统的自动编码器(Auto Encoder，AE)演变改进而来[6]。

AE的概念是在1986年有Rumelhart提出的，起初主要被应用于高维数据的降维处理，其主要结构可以用图7表示。

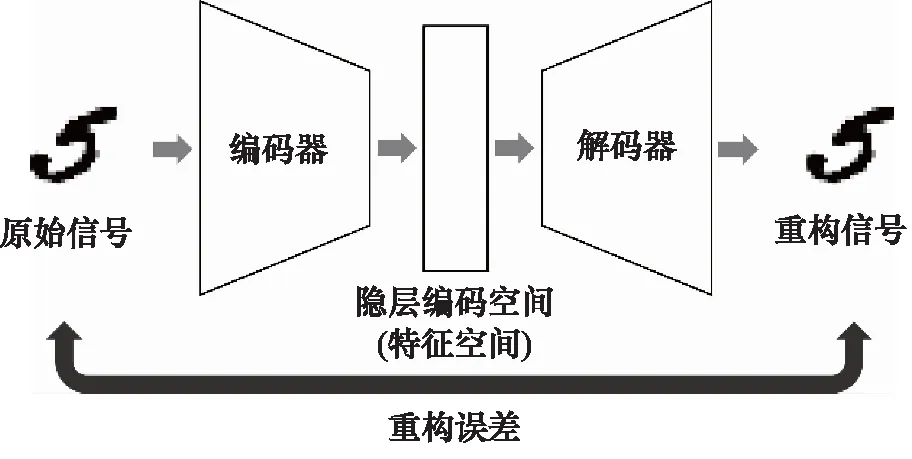
图7 自动编码器(AE)结构示意图Fig.7 Schematic of Auto Encoder (AE)

从AE的结构图可以看出，AE的目的是通过尽可能降低重构误差，从而使输出的重构信号最接近于原始信号[9]，这时隐层编码空间所提取出的特征是最能够表征原信号的。

AE可以用以下公式进行描述：

h=en(x)=sen(wenx+ben)

(1)

(2)

(3)

而VAE相较于AE，最重要的区别是假设潜在变量h的后验分布服从独立的多元高斯分布。因此编码器不再直接生成潜在变量，而是先生成一组潜在变量所属的高斯分布的均值和方差，然后经过随机采样，在这些分布中取得一组潜在变量h作为解码器的输入。这样做的目的是在解码前向潜在变量中加入了噪声，从而使整个网络鲁棒性更好，能够提取出类似于训练样本信号，但不完全相同的新信号的特征，VAE的主要结构如图8所示。

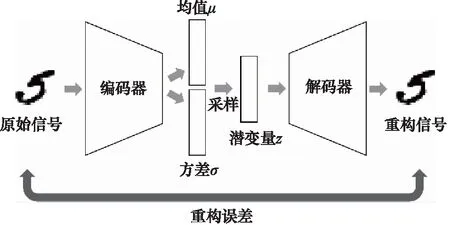
图8 变分自动编码器(VAE)结构示意图Fig.8 Schematic of Variational Auto Encoder (VAE)

VAE可以用以下公式进行描述：

μ=en(x)=sen(wenx+ben)

(4)

logσ2=en(x)=sen(wenx+ben)

(5)

h=μ+ε×σ

(6)

KL(N(μ,σ2)‖N(0,1))

(7)

式(4)、式(5)中表示编码器现在并非直接生成潜在变量，而是生成一组均值和方差。其中μ和σ2分别是潜在变量所属的一组高斯分布的均值和方差。之所以选择logσ2作为编码器的输出，是因为σ2总是非负的，要使网络拟合σ2就必须加激活函数进行处理，而logσ2可正可负，省去了这一步骤。式(6)是1个重参数技巧，它的作用是将在潜在变量所属的分布中采样得到潜在变量的这一“采样”过程变得可导，从而能够进行梯度下降求最优化。具体而言，因为如果直接从N(μ,σ2)的分布中采样，那么“采样”的过程本身是无法求导的，那么自然也无法进行误差传递。但从1个N(μ,σ2)中采样1个潜在变量h，是等价于从N(0，1)中采样1个ε，并通过式(6)计算得到潜在变量h的，这样一来通过式(6)就可以进行梯度下降了。式(7)是VAE的损失函数，相比较于式(3)AE的损失函数，区别主要在与增加了1项KL(N(μ,σ2)‖N(0，1))。这一项衡量潜在变量所属分布与标准正态分布之间的KL散度，即相似程度，目的是使所有的潜在变量分布都向标准正态分布看齐，避免训练过程中σ2趋近于0，VAE向AE退化。

2.2 模型结构

由于样本是3通道的一维时间序列，所以编码器和解码器的基本结构采用了一维卷积神经网络，网络的结构如图9所示。图中的圆圈序号代表网络中的“层”；方框代表在“层”之间传递的数据，即张量；方框中的数字表示张量的尺寸。

图9 VAE故障诊断模型结构示意图Fig.9 Schematic of VAE based fault diagnosis model

其中①～⑦层构成了编码器：①～④层为一维卷积层，⑤层和⑨层为展平操作，⑥层和⑦层为全连接层，输出分别为式(4)和式(5)中的均值和方差；⑧层为式(6)所对应的重参数采样操作；⑩～层构成了解码器：⑩层为变形层，～层为反卷积层；层为以隐层均值向量作为输入，以分类结果作为输出的一个多层感知机分类器，作用是根据提取出的隐层特征，对样本进行分类预测，再将预测标签与样本真实标签组合计算损失，将此损失定义为分类损失，即图中的Cat-Loss。

因此，该VAE故障诊断模型的总损失误差除了由式(7)定义的重构误差和KL损失外，还增加了下式的分类误差：

Losscat=cross_entropy(y,ypred)

(8)

ypred=cat(μ)=scat(wcatμ+bcat)

(9)

式(8)为真实标签和预测标签的交叉熵；式(9)表明预测标签来自于分类器cat(·)，其中scat是分类器激活函数的集合，wcat是分类器中神经元权重的集合，bcat是分类器中神经元偏置的集合。

该模型的总误差为：

Lossall=Lossrecon+LossKL+Losscat

(10)

其中Lossrecon和LossKL由式(7)定义，Losscat由式(8)定义。

2.3 模型训练及测试结果对比

本研究的模型搭建均在TensorFlow平台上完成。模型的训练均在如下设备上进行：CPU：Intel(R) Core(TM) i7-8700 CPU @ 3.20 GHz，3.19 GHz；GPU：NVIDIA GeForce GTX 1660；RAM：8G。

为了通过对比体现出该VAE模型在故障检测任务中性能的提升，本研究选择的对照模型是通过先手动对数据集进行特征提取，再搭建BP神经网络分类器进行训练得到的模型[1-2]，下面称为小波包特征模型。特征提取的方法为对三通道信号分别进行小波包分解，提取各层小波包系数作为特征向量。对每个通道的信号进行4层小波包分解[1]，得到长度为16的特征向量，故每个样本可提取出长度为48的特征向量。

如图10所示为进行特征提取后，通过t-SNE方法对测试集样本进行降维的聚类图。图例所示为样本的真实标签，0，1，2分别代表健康、阀芯卡塞和密封件损坏。可以看出，通过小波包分解提取出的特征向量比较难以直接将不同工况下的样本区分开。而如图11所示为VAE模型进行特征提取后，在隐层空间中对样本的特征进行t-SNE降维聚类图，相比于图10，VAE模型提取出的特征则能较好的区分不同工况。然而因为前述章节提到，同一工况的数据是在不同的子工况，即不同气压、不同工作频率下采集的，因此可以看到，VAE模型提取出的特征将这些子工况也被聚在了不同的簇。

图10 小波包能量特征降维聚类图Fig.10 Dimensionality reduction clustering diagram with wavelet packet energy as feature

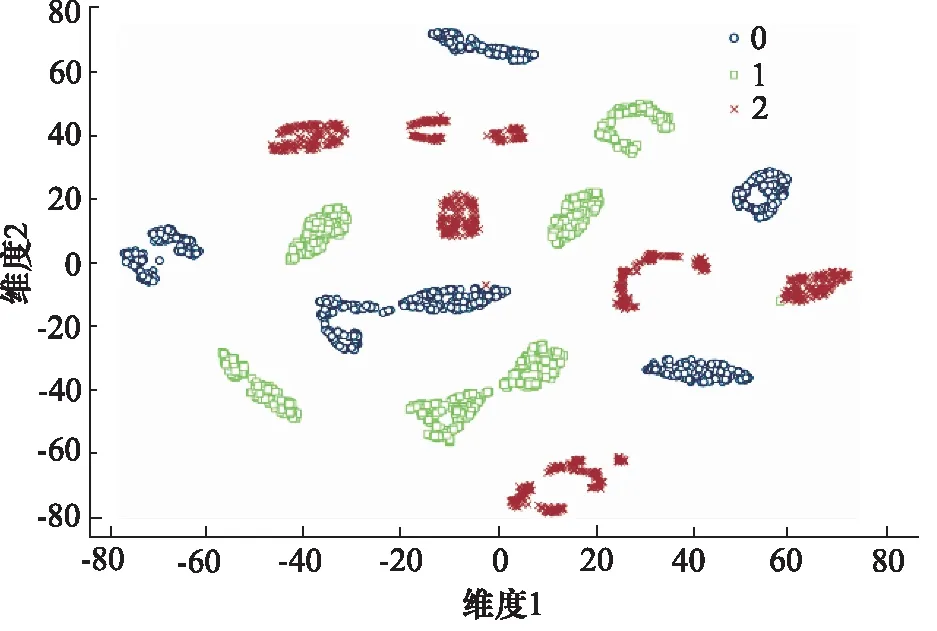
图11 VAE模型隐层特征降维聚类图Fig.11 Dimensionality reduction clustering diagram with VAE model

可以预见的是，这样的模型对于新的工作频率或新的工作气压下采集的样本的泛化能力将会较差。如果能使模型在提取特征时忽略不同子工况之间的差异，即在特征降维聚类图中将同一工况的样本尽可能聚在一起，将不同工况的样本尽可能分开，则模型会具有更好的泛化能力。接下来将会优化模型，对这一设想进行验证。

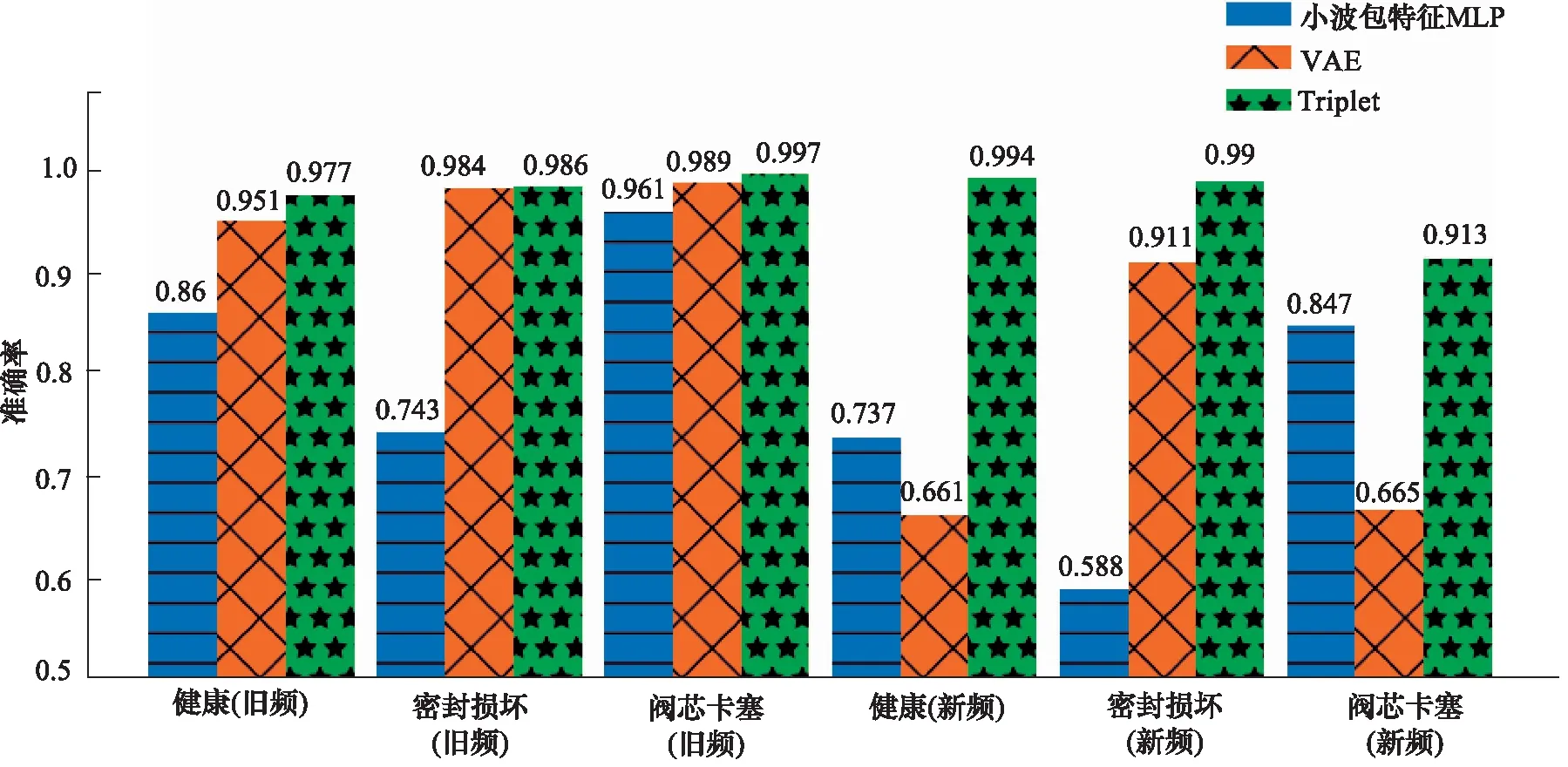
如图12所示是小波包特征模型和VAE模型对于不含及含有新频率样本的测试集的准确率对比。对于不含有新频率样本的测试集的3种工况，VAE模型的准确率均高于小波包特征模型。其中对于健康工况，准确率由86.0%提升至95.1%；对于密封件损坏工况，由74.3%提升至98.4%；对于阀芯卡塞工况，由96.1%提升至98.9%。这说明本研究提出的VAE模型对于电磁阀故障检测问题，能够自动提取出信号中更具有区分能力的特征，然后利用特征进行故障检测。这相较于先对电磁阀工作信号进行手动特征提取，再构建故障检测模型的方式，在便捷性、自动化程度识别准确率上都有明显的提升。

图12 小波包特征模型和VAE模型对试集准确率对比Fig.12 Comparison of accuracy of wavelet packet feature model and VAE model on test sets

但是，同时也容易看出该VAE模型对于含有新频率样本的测试集的准确率比较低。

3 基于Triplet loss的改进电磁阀故障诊断模型

3.1 Triplet loss

Triplet意为三元组，这样命名的原因是对于训练中的一个batch(以下称为批次)，需要将所有样本划分为3个一组的三元组，计算每个三元组的损失，然后求和[11]。图13所示是Triplet loss(以下称为三元组损失)的训练目标。每一个三元组的构成如下：从训练数据集中随机选1个样本，该样本称为 Anchor，即锚样本，然后再随机选取1个和锚样本属于同一类的样本和不同类的样本，这2个样本对应的称为 Positive和 Negative，即正样本和负样本，由此构成1个(锚样本，正样本，负样本)三元组。三元组损失的目的就是通过学习，让同类样本的特征表达间距尽可能小，而异类样本的特征表达间距尽可能大。

图13 Triplet loss训练目标示意图Fig.13 Schematic diagram of Triplet loss training target

三元组损失的计算公式为：

Losstri=max{d[f(a),f(p)]-d[f(a),f(n)]+

margin,0}

(11)

其中f(·)代表编码器网络，在本研究中，即式(1)中的en(·)；d[·]代表距离计算函数。f(a)，f(p)和f(n)就表示3种样本在隐层空间中的表示。

在1个批次中，首先需要生成所有三元组，然后筛选出有效的三元组，用这些有效的三元组计算损失，然后进行误差反向传播，梯度下降训练模型。之所以不是所有的三元组都有效，是因为在每个批次中的所有三元组中，三元组的性质存在这些可能：

(1) Easy Triplets，满足：

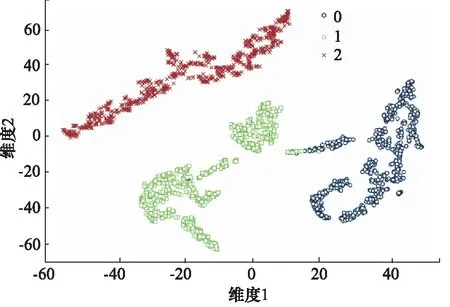
d[f(a),f(p)]+margin

(12)

即负样本与锚样本的距离已经大于正样本与锚样本的距离，且满足间隔裕量margin。此时损失L为 0。这种三元组(Triplet)是不需要训练的，因为它的损失已经为0，将它加入整个批次的损失函数中对训练的方向没有帮助。

(2) Hard Triplets，满足：

d[f(a),f(p)]>d[f(a),f(n)]

(13)

即负样本与锚样本的距离小于正样本与锚样本的距离。此时损失大于margin。这种三元组和下面的Semi-Hard Triplets都是有效的，但是具体使用哪一种则可以根据具体任务选择。

(3) Semi-Hard Triplets,满足：

d[f(a),f(p)]

(14)

即负样本与锚样本的距离虽然大于正样本与锚样本的距离，但是还不满足间隔裕量margin。此时损失小于margin但大于0。

图14直观地展示了3种三元组的分布。图中A和P分别代表锚样本样本和正样本，根据负样本和前两者的距离关系，三元组被分为不同的类别。本研究提出的改进模型中，对每个batch中的每个样本，只选取Hard Triplets和Semi-Hard Triplets进行三元组损失的计算。

图14 三种三元组的分布Fig.14 Distribution of three kinds of triples

3.2 模型结构

基于三元组损失的改进模型结构图如图15所示。和图9所示模型结构相比，主要区别在与在圆圈序号17处增加了一个自定义层，用于通过隐层特征计算每一个样本批次的三元组损失。这个新增的层在图15中用虚线框做以标记。

图15 基于Triplet loss的改进模型结构图Fig.15 Schematic of improved model based on Triplet loss

此时的模型训练将分为两个步骤：

Lossall=Lossrecon+LossKL+Losstri

(15)

步骤一的目的在于通过最小化上述损失，使模型能够提取出既能够表征原信号，又能将同一类别(健康、阀芯卡塞或密封件损坏)的样本聚为一类，将不同类别的样本区分开的隐层特征。

步骤二：固定除了分类器之外的编码器、解码器的权重和偏置，只训练分类器的权重和偏置。这时候的目标函数仅为分类器的分类误差：

Lossall=Losscat

(16)

当两个步骤训练完成后，整个模型也就训练完成了。

3.3 模型训练集测试结果对比

如图16所示是使用训练好的改进模型对测试集样本进行特征提取后，对隐层特征使用t-SNE降维后的聚类图。可以看到，相较于图11所示的VAE模型的特征提取效果，改进模型在特征提取上能够很好地将同一工况的样本聚为一簇，忽略其中各子工况之间的差别。

图16 改进模型隐层特征降维聚类图Fig.16 Dimensionality reduction clustering diagram with improved model

如图17所示是小波包特征模型、VAE模型以及改进模型，对于不含及含有新频率样本的测试集的准确率对比。可以看到，因为VAE模型本身已经对旧频部分准确率较高，所以改进模型在仅含有旧频样本的测试集上准确率只有较小的提升；而在测试集的新频部分，改进模型的提升则非常明显，对3种工况都达到了90%以上的准确率，其中对于健康工况，准确率由VAE模型的66.1%提升至99.4%； 对于密封件损坏工况率由91.1%提升至99.0%； 对于阀芯卡塞工况，准确率由66.5%提升至91.3%。这表明了改进模型很好地解决了前述章节提出的VAE模型对于新的工作频率下采集的信号识别准确率低的问题，提升了模型的泛化能力。

图17 小波包特征模型、VAE模型和改进模型对测试集准确率对比Fig.17 Comparison of accuracy of wavelet packet feature model, VAE model and improved model on test sets

概括地来说，加入了三元组损失的模型之所以能够对训练集中没有的新的工作频率样本有更高的识别准确率，是因为无论是改进前还是改进后的模型，其最重要的部分都是一个有监督的，用于提取特征的网络。而改进后的模型相较于改进前，在三元组损失的作用下，网络在提取特征时趋于弱化同工况下不同子类(即不同的工作频率)之间的差异、强化不同工况之间的差异。这在图11和图16的对比中可以明显体现。

当训练后的网络可以几乎忽视不同子类之间的差异信息而对样本进行特征提取时，网络就可以只利用和工况相关的信息对样本进行模式识别。此时使用训练集中没有的新的工作频率下采集的测试集对网络进行测试，就可以获得很高的准确率。而从隐藏层特征聚类的角度来看，即新工作频率的测试样本在图16所示的隐层特征降维聚类时，因为和工作频率相关的信息在特征提取过程中已经被网络忽略，只保留了和工况相关的信息，从而仍然可以和已知的同工况样本聚在一起，因此能够准确地进行模式识别。

4 结论

针对电磁阀故障识别对专家知识依赖过高的问题，以某型号电磁阀为研究对象，采集了数据集，构建了基于VAE的端对端故障检测模型，与传统故障检测模型对比有较好的性能提升。针对所提出VAE模型的泛化能力较差的问题，基于三元组损失对模型进行了改进。实验表明，经过改进的模型的泛化能力得到了很好的提升，对于训练中未见过的工作频率下采集的信号也具有很高的识别准确率。最后，由于实验对象型号的电磁阀的真实故障样本较难获取，本研究在信号采集方面参考了目前电磁阀故障诊断常用的故障模拟方法[1，3]，在本研究的研究主题下，认为这种故障模拟方式和信号采集方式能够在一定程度上反映真实故障工况，是合理的。同时，将本模型针对真实发生故障的电磁阀进行模型训练、改进和验证，是本研究未来的工作中的一大重点。