基于PCK视角的高中数学概念教学研究
2022-09-20江苏省苏州实验中学
江苏省苏州实验中学
王 莉
1 引言
数学概念能够从本质上反映知识点,多数的数学知识都会围绕特定的核心概念展开.概念教学是高中数学教学体系中的重要版块,通过概念教学旨在让学生形成对概念以及基本思想的理解.学科教学知识(PedagogicalContentKnowledge,PCK)的概念最早由美国教育研究会主席Shulman提出,他指出在教学中知识基础共有七类,其中学科教学知识是重点与核心.他主张将教学学科的内容与教育学知识相结合,根据不同的教学知识内容的差异化使用教学方法与策略.笔者基于相关理论以及前人研究,以“任意角三角函数的概念”为例,探究PCK视角下高中概念教学设计的相关问题,以期为广大师生提供教学参考.
2 掌握教材,了解学生,熟练教法
教材是教学活动最主要的依据,是知识内容最重要的来源.在研究教材时,教师要充分结合课程标准要求,认真思考教学目标,思考教学内容与全章节甚至是整本教材内容之间的关联性,明确教学重点与难点,仔细研判例题与练习题,判断能否延伸拓展.在备课过程中,除了要利用好教材,教师还需要借助课程标准、教辅资料、互联网教学资源等补充教学内容.
学生个体之间存在较大的差异性,在概念教学的过程中,教师要根据学生的特点,强化概念形成过程的讲解,引导学生用适当的方法参与学习.同时,教师还需要准确评估学生已有的知识能力水平,牢牢把握教学的起点.除此之外,教师还需要关注学生的情感与态度,加强德育教育,引导学生全面发展.
在明确教学内容和学生特点的基础上,教师还需要选择合适的教学方法,预先设计好概念引导的方式.比如,是采用形成还是同化的模式来讲解相关概念;思考如何让学生参与概念形成的探究过程,充分理解并合理运用概念.课堂教学方法科学与否不仅会影响学生对概念原理的掌握,也会影响学生数学思维的形成与发展.
3 构建概念教学结构体系
基于PCK视角的概念教学更加注重概念之间以及与其他数学知识之间的关联性,因此在完成以上教学准备工作后,教师还需要深入挖掘,从更大的内容体系背景下优化教学方案.随着教学内容的深入以及学生自身年龄的增长,学生对于复杂、抽象的数学概念的接受能力增强,思维整体性也不断提升,因此教师在开展概念教学的过程中,不仅需要帮助学生掌握相关概念内涵,还需要提升学生思维的整体性,加强学生对宏观知识架构的认知与理解,引导学生在一定知识积累的前提下,借助自己的认知构建网状的知识框架,串联相互关联的知识内容.
4 强化数学概念的形成教学
概念教学的基础环节就是概念引入,主要有“直观引入”和“实际需要引入”这两种方式,这一步会直接影响学生对概念的理解.“直观引入”需要结合现实事例或者是客观物体,减弱概念的概括性、抽象性给学生造成的干扰,帮助学生真正理解概念的内涵以及蕴含的数学思想,加深记忆,强化理解.比如在讲授“概率”的概念时,可以借助抛硬币、我国人口普查等实例来激发学生对概率的初步理解,通过“提出问题—结合实例—引发思考—概括概念”的教学过程引导学生充分参与概念的生成过程,加强直观感受;“实际需要引入”则是强化相关概念的实际问题背景,常用的教学思路就是结合数学史来开展概念教学,将特定需求以及相关概念结合起来,加深学生对数学知识应用的认知.
在引入概念之后,需要强化学生对概念的理解,这是PCK视角下概念教学的核心环节.教师需要借助不同的问题情境、例题等突出概念的本质特征,多层次、全方位地进行概括,在此基础上引导学生基于个人理解,用简洁的语言来描述相关概念的特征并注重与其他概念的比较.在理解概念之后,还应设计概念巩固的教学环节,让学生自行叙述对概念的理解,向学生提出容易混淆的概念要点,巩固概念教学的成果.
5 教学设计——以“任意角三角函数的概念”为例
基于PCK的内涵,笔者以“任意角三角函数的概念”教学为例,通过“教材及学情”“目标与重难点”“教学过程”等环节的研究,探究PCK视角下高中数学概念教学的实施路径与改进策略.
5.1 教材及学情
“任意角三角函数”是人教A版必修一第五章第二节的教学内容,是对之前所学函数概念的补充与延伸,也是后续诱导公式、三角函数图象与性质、和差公式等教学内容的前提,因此具有重要的衔接作用.在初中阶段,学生已经接触过锐角的三角函数,具有一定的知识基础,但是也要让学生明白二者的差别.锐角三角函数是指直角三角形中不同边之间的比值,而任意角的三角函数则是指角终边上一点的坐标与圆的半径或者坐标之间的比值,这是任意角的三角函数与之前学生接触的锐角三角函数概念的最大区别,也是本节概念教学的基础.
5.2 目标与重难点
对于“任意角三角函数的概念”这部分内容,要求学生区别于锐角的三角函数概念,准确定义,能够用坐标系中角的终边和单位圆的交点坐标来表示,明确三角函数在不同象限的正负特征.任意角三角函数的概念以及定义域是本节教学的重点,难点为明确三角函数的内在关联性.
5.3 教学过程
5.3.1 创设情境背景
地球的自转公转、月亮的圆缺变化、物理中的圆周运动、时钟指针转动,这些变化过程都具有交替往复的特征,为了准确描述任意的运动特征,将初中0°~360°的角度范围进行延伸,扩大至任意角.假设单位圆O上的点M,以A为起点按逆时针方向运动,如果∠AOM=α,那么就可以用α来描述M点的位置.
设计意图:不同于初中阶段利用直角三角形来引入三角函数的概念,基于PCK理念,利用学生所熟悉的学科知识或者是生活现象创设情境,用圆周运动来引入教学内容,同时也能加深学生对于多学科交叉思维的认知.
5.3.2 引导探究
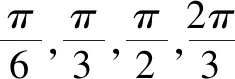
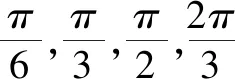
5.3.3 重难点解析
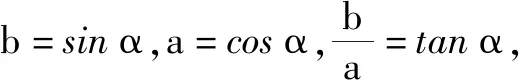
设计意图:三角函数的定义域是本章的教学重点,其中正切函数的定义域又是难点.基于PCK理论视角,教师需要具备丰富的学科知识,能够准确把握教材中的重难点并设计相应的教学环节进行突破.
5.4 改进策略
基于学科教学知识(PCK)的概念教学需要教师不断总结教学过程,对教学目标以及重难点的形成准确判断,并充分结合班级学生的学习诉求,认真反思,及时调整教学策略,不断丰富自身的学科教学知识,优化其结构;同时,也要及时更新与教学相关的技术与手段.
