借助三角形外心 巧妙求解代数式

江苏省海安高级中学

叶枝凤

平面向量是历年高考数学的一个重要知识点，是高考的热点与重点问题之一，由于其同时兼备“形”的特征与“数”的性质，问题设置新颖多样，内涵丰富背景创新，变化多端思维各异，是数学学科中知识与能力充分交汇与融合的理想场所，具有很好的选拔性与区分度，倍受命题者青睐.

1 问题呈现

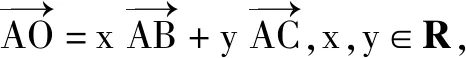
此题以三角形为载体，结合确定的三角形以及外心，通过含参数的平面向量的线性关系式的建立，进而求解对应参数的一次代数关系式的值.破解此类问题，关键就是要抓住平面向量中的“形”的特征、“数”的性质或“形”与“数”的和谐统一，从平面几何角度加以直观处理，平面向量角度加以转化，坐标角度加以运算等，从而解决相应的问题.

2 问题破解

思维视角一：平面几何思维.

解法1：(平面几何法)如图1所示，取AB的中点D，在AC上取一点E，使AC=3AE，连接OD，OE，DE，其中OA交DE于点F，则AD=1，AE=1，OD⊥AB.而∠BAC=60°，则知△ADE为正三角形，从而DE=1，∠ODE=30°.

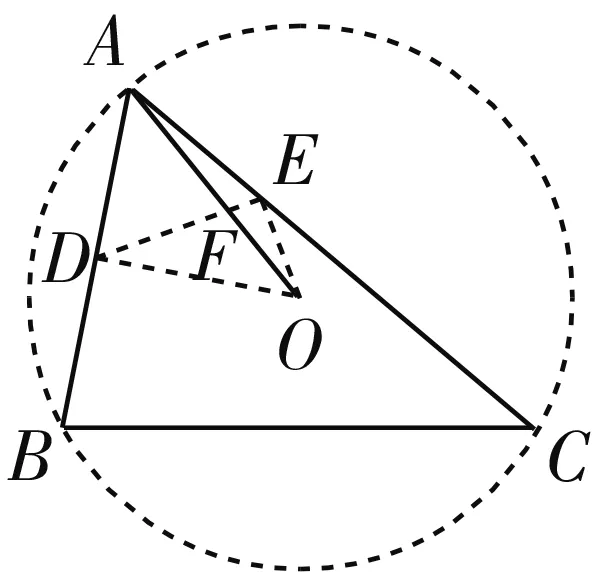
图1

在△ABC中，由余弦定理，可得

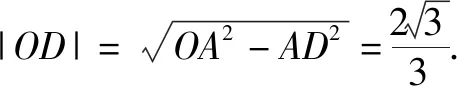
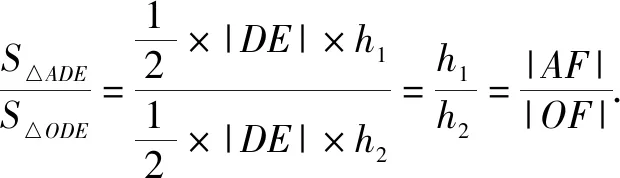
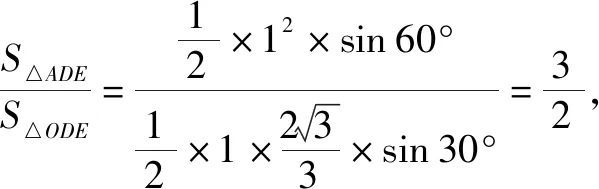
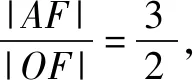
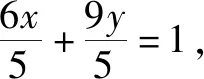
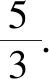
点评：根据平面向量“形”的特征，以及平面向量的线性关系式，通过三角形图形的直观，结合余弦定理与正弦定理的应用，利用三角形面积的转化确定对应边长之间的比值，从而把平面向量的线性关系式转化为以A为起点的三个共线的向量之间的线性关系式问题，利用共线向量的性质建立关系式来求解.

思维视角二：平面向量思维.

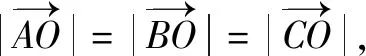
图2

结合余弦定理的向量式，有

所以，4x+3y=2.

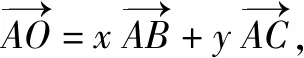
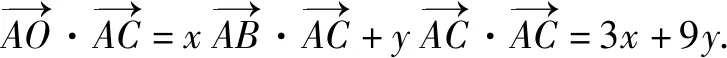
结合余弦定理的向量式，有

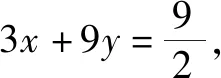
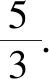
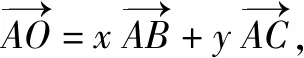
所以，4x+3y=2.

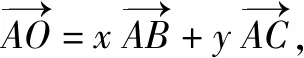
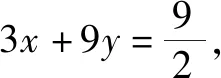
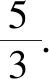
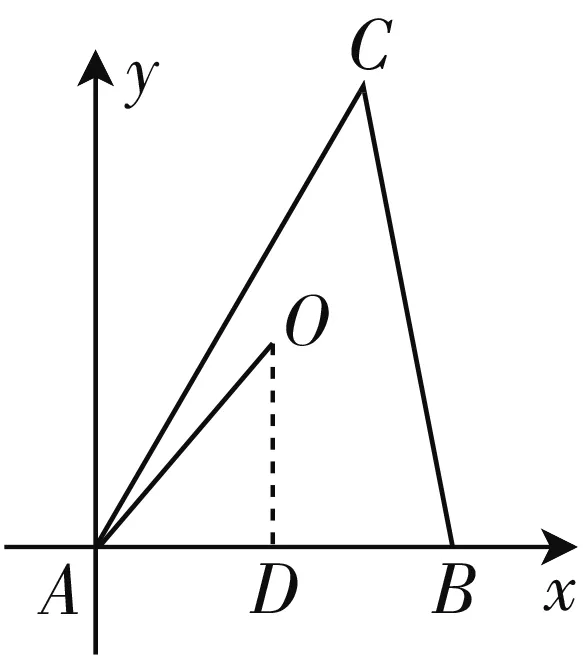
图3

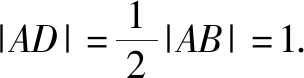
在△ABC中，由余弦定理，可得

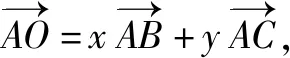
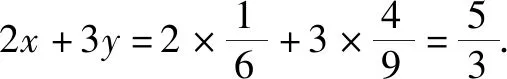
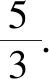
点评：根据平面向量“形”与“数”的和谐统一性，建立相应的平面直角坐标系，先确定点C的坐标，利用三角形外心的性质，综合解三角形中的余弦定理和正弦定理，以及勾股定理来确定外心O的坐标.利用坐标运算代入平面向量的线性关系式，建立相应参数的一次方程组，通过求解参数值，进而得以求出一次代数关系式的值.不同的建系法都可以达到破解的目的，只是相应的点的坐标发生了变化.

3 解后反思

借助平面向量“形”的特征与“数”的性质的双重身份，破解此类问题时，可以从“形”的角度入手，利用几何直观，通过平面几何特征或图形直观等形式来处理；可以从“数”的角度入手，利用代数视角，通过代数运算或平面向量的运算等形式来解决；还可以从“形”与“数”的和谐统一性，通过坐标运算等形式来破解等.涉及平面向量的相关问题，能有效达到问题设置的多知识融合，思维方式的多角度切入，破解技巧的多方法处理等，是充分考查数学知识，提升数学能力，培养数学核心素养的好阵地.