古典概型教学中德育元素的挖掘和渗透

吉林师范大学

陈嘉楠

1 引言

在初中学习的基础上，我们知道对某些事件概率的估计可以通过试验或者观察得到.但是通过试验或观察所得事件的概率只是近似值，而且此方法耗时较长.因此，在总结试验的共同特点(如有限性、等可能性等)的基础上，进而得到随机事件概率的一个重要的数学模型，即“古典概型”[1].

古典概型的教学不仅可以帮助学生树立辩证唯物主义的世界观，还可以了解古典概型的相关数学史知识.本文中通过分析部分经典的古典概型的例题，挖掘和渗透题中蕴含的德育元素，使古典概型教学与德育教学有机结合，在培养学生解题能力的同时提高其思想水平[2].为此，可从以下几个方面进行古典概型教学中的德育元素的挖掘和渗透.

2 古典概型中有关公平性的问题

例1某家超市搞活动，规定当天消费满500元的顾客可以参与抽奖，符合要求的顾客共有6人，这6个人依次从6个标有从A到F字母的小球中不放回随机抽取一个小球，抽到标有字母C的小球可获得奖品，这样公平吗？

解：依题意可知，第一个人抽到C球的概率为

第二个人抽到C球的概率为

第三个人抽到C球的概率为

类似地依次下去，可得第六个人C球的概率为

综上可知，每个人抽到C球的概率都是相同的，所以这个抽奖方式是公平的.

3 古典概型中有关垃圾分类的问题

例2当前环境问题是热点话题.某地区为响应国家号召，主动对生活垃圾进行全方位的分类处理，将生活垃圾分为表1中所展示的三类.现对该地区居民的垃圾分类状况进行调查，三类垃圾箱中总计1 000 t生活垃圾，数据统计如表1所示(单位：t).

表1 生活垃圾分类数据统计表 单位：t

(1)试估计厨余垃圾投放正确的概率；

(2)试估计生活垃圾投放错误的概率.

分析：首先例2的两问均满足样本点有限，并且垃圾投放到三个垃圾箱是等可能的，所以属于古典概型.本题考查了古典概型的概率和对立事件的概率计算.

解：(1)记M=“厨余垃圾投放正确”，则

(2)记A=“设生活垃圾投放错误”，则

在课堂教学中讲解古典概型时，可引入垃圾分类等与生活密切相关的例子，通过垃圾分类试题的讲解，能够让学生更加明确垃圾如何分类，了解垃圾分类的重要性，形成保护环境的意识[3].

4 古典概型中有关赌博性的问题

例3有一种赌博游戏叫做抓彩珠游戏，游戏规则是总共有27颗珠子，有3种颜色，每个颜色9颗，参与者从袋子里任意拿出9粒，按抓出珠子颜色个数的比例与摊主进行兑换.兑换规则如表2.(10元20次)

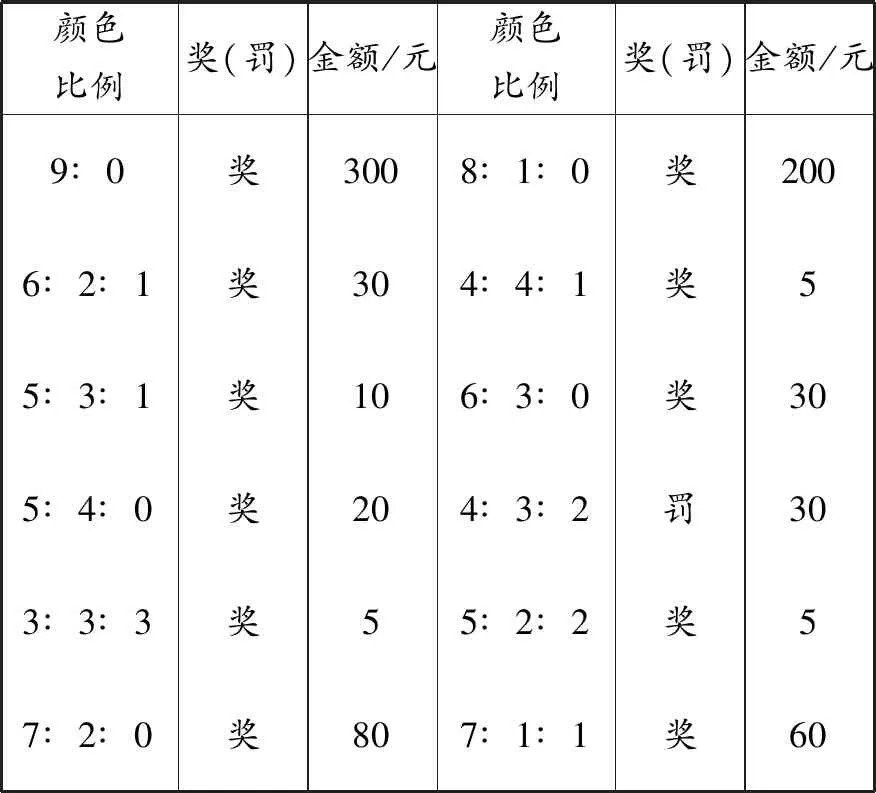
表2 游戏奖罚金额兑换规则

问：20次游戏后可能会输掉多少元？

解：由于每个样本点发生的可能性相同，并且样本空间的样本点只有有限个，于是此游戏满足古典概型要求.可以计算得出

=6.400 9×10-7;

=1.036 9×10-4;

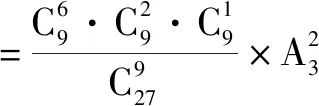
=0.034 8;

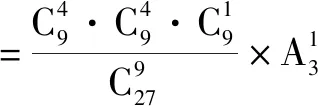
=0.091 5;

=0.121 9;

=0.009 0;

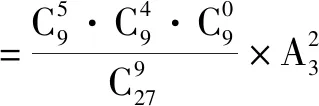
=0.020 3;

=0.487 8;

=0.001 7;

根据上述的计算结果发现，能够中200元和300元的概率是极小的，基本没有出现的可能.虽然在奖罚方面上表面呈现的绝大部分都是中奖，只有一个是罚款30元，但“罚款30元”从概率角度来说是比较高的，接近50%.因此，最终的奖罚总量上是罚钱占主导的[4].根据概率，可知每进行一次游戏奖(罚)金额均值为

N=300×6.400 9×10-7+……+0.487 8×(-30)+……+0.001 9×60≈-9.81(元).

也就是说，每次游戏可能会输掉9.81元，则20次游戏后，将可能会输掉196.2元.

因此，教师在进行古典概率教学时，应让学生明白这场赌博游戏背后的科学道理，用科学的计算结果让学生警惕这种以金钱为赌注的游戏，让学生对赌博的认识从感性上升为理性，明白赌博对任何人都是无利的，培养学生正确的价值观.

5 古典概型与数学文化

我国古代早在三千多年前就已经产生了与概率相关的思想，从《周易》中有关“卦”“爻”等内容追溯，书中有关于占卜、演算等内容.用现代的观点看“卦”，其本质是一种随机试验[5].以我们最熟悉的抛硬币试验来类比，如果用硬币“正面朝上”来表示“阳爻”，硬币“反面朝上”来表示“阴爻”，连续进行3次试验，其样本空间有8个样本点，即可画出《周易》中的八卦图；同理连续进行6次试验，其样本空间有64个样本点，即可画出64卦图.由此可以看出《周易》中蕴涵深厚的古典概型思想，这是一种历史唯物主义的辩证思想[6].

古典概型作为学生应用数学文化意识不可缺少的重要数学模型，逐渐进入了高考命题者的视野.以2019年全国卷理科数学选择题第6题为例.

图1

分析：这道试题的背景即是《周易》中有关我国古代古典概型相关思想的记载.要解决此题，先要明确试验的条件及要观察的结果，重卦的排列是由6个“爻”从下到上组成，在每个重卦中，有6个不同的位置，这6个不同位置的爻都有“阴爻”和“阳爻”两种可能，符合古典概型的条件.

解：由每一“重卦”由从下到上排列的6个爻组成，爻分为阳爻和阴爻，所以样本空间中元素个数为

26=64，

即共有64种不同的结果.记A=“重卦中恰有三个阳爻”，则事件A包含的样本点数为

故选择：A.

从数学史研究和数学文化渗透的角度来赏析，这道题不仅对《周易》中的数学史料进行了挖掘，而且在一定程度上将古典概型同“卦”“爻”等内容相结合，有利于学生数学文化意识的发展和应用.同时，也启发教育工作者在古典概型以及其他课程的教学中把数学史与数学文化知识恰当结合，使学生能够更好地应对未来高考的变化，更深刻地理解数学模型的生成和应用过程，感受中国传统文化的悠久历史.

6 体育赛事中的古典概型问题

例5运动赛场上，某射击运动员不受外界影响在同一条件下进行射击[7]，其成绩如下表3.

表3 运动员射击成绩分析

(1)计算表3中命中靶心的各个频率，填入表中；

(2)估计该运动员射击一次命中靶心的概率.

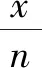
解：(1)表中应填入的频率依次为0.80，0.95，0.88，0.92，0.89，0.91.

(2)由于填入表3中的频率数据趋近于0.89这一常数，所以该运动员射击一次，命中靶心的概率约为0.89.

人教A版数学必修第二册(2019年版)第238页练习1便是运动员飞碟射击问题，教师可以由此扩展，引导学生关注奥运会的相关赛事.奥林匹克运动历史悠久，是人类文明的宝贵遗产.教师应引导学生关注奥运会和国家大事，培养学生热爱体育、热爱生活的美好信念和自我驱动力.

7 结语

本文阐述了在古典概型教学中挖掘和渗透德育元素，使古典概型教学与德育教学有机结合，通过对古典概型在公平性问题、赌博性问题以及垃圾分类等方面的应用分析，学生在学习知识的同时，自身的思想道德水平也得到一定的提升.

此外，德育元素不仅可以融入古典概型教学中，还可以融入高中数学其他课程教学中.这需要教育工作者们不断发掘课程中的德育元素，对教科书内容进行合理拓展，提出与时俱进的热点与难点，以实现高中数学课程和德育教学的有机结合，进而有效达成知识传授与德育渗透的更好融合.