埋地输气管道对城市地下空间掘进爆破的力学响应*

孙宝财，凌 晓，周文海，王树江

(1.甘肃省特种设备检验检测研究院，兰州 730050；2.兰州理工大学 石油化工学院，兰州 730050；3.中国石油大学(北京) 机械与储运工程学院，北京 102249)

近年来我国城市地下空间工程广泛采用掘进爆破的方式进行开挖，同时对临近爆破区域已有埋地输气管道的安全稳定运行问题提出了巨大挑战。爆破过程中地震波通过岩土体传播到管道和地表，一旦地震波强度超过管道屈服强度，管道则发生较大的塑性变形，甚至造成屈服破坏。

目前为止，已有不少学者通过试验和数值计算的方法对该问题做了相关研究[1,2]。张黎明等基于管道屈服破坏的应变准则创建了管道破坏时临界应变值与地表质点振动峰值速度之间的数学模型[3]，并利用试验监测的振动数据对管道可承受最大允许峰值振速进行了判断。朱斌等通过下穿预埋燃气管道的现场爆破试验[4]，并结合应变分布特性和应力波传播理论对地震波传播规律进行分析。研究指出管道允许的应变峰值为366.4×10-6，地表最大安全控制振速为8.5 cm/s。夏宇磐等以青岛地铁下穿给水管道隧道爆破为工程背景[5]，结合现场试验和数值模拟方法对给水管道的动力响应特性进行了研究，同时还建立了管道的有效应力和地表质点振速间的数学模型。指出类似这种钢筋混凝土管的极限动态抗拉强度约为2 MPa，确保管道安全的地表振速应控制在3.3 cm/s以内。郑爽英等同样以下穿既有输气管道的隧道爆破工程为背景[6]，利用数值模拟结合正交试验的方法对管道应力与振速响应特征影响的5个因素(管径、壁厚、管深、管道与隧道净距、管道内压)进行了研究，指出管道应力分布主要受内压和壁厚的影响，管道运行时的最大动应力可叠加空管动态应力峰值和有压静载状态的主应力进行估算。梁政等同样通过控制变量法[7,8]，分析了不同爆源间距、管道壁厚和装药量下的管道受载情况。Kouretzis等在不考虑管道周围岩土体对管道挤压作用的前提下[9]，给出了爆破载荷作用下管道受载的解析解，并与实际工程案例进行了对比，验证了其理论的准确性。Mirzaei等分别采用试验[10-13]、数值模拟以及两者对比的方式对工程爆破近区的管道受载机制和动态响应情况进行了深入研究。Nan Jiang等利用动力有限元软件建立了3D爆破模型[14]，通过数值计算结果和现场监测数据的对比，对管道和管道近区岩土体的振动效应进行了研究。王飞等采用数值模拟的方法对天然气管道在爆破载荷作用下的变形情况、应力应变分布以及破坏模式进行了分析研究[15]。

依托某一具体城市地下掘进爆破实例，采用动力有限元软件LS-DYNA建立岩土流固耦合模型，对爆源近区管道受载情况以及动力响应机制进行了研究，主要分析了管道迎-背爆面有效应力的分布情况、管道上振动波传播规律以及衰减情况，为类似工程爆破安全施工提供理论指导。

1 管道弹塑性理论

在冲击载荷作用下，管道的变形通常有体积和形状改变，体积改变是由各向相等的应力引起，一般表现为弹性性质，而管道塑性变形是由于形状的改变而引起。管道任意质点处受力状态可分解为两部分，即球形应力张量σm和偏斜应力张量sij，总应力方程为

σij=σm+sij

(1)

任意一点处主平面方程可表示为

(σij-δijσn)lj=0

(2)

式中：δij为Kronecker符号；σn为主应力;lj为方向余弦。

由(2)式展开的线性方程有非零解的充要条件是系数行列式等于零，并将式(1)带入系数行列式可得

(3)

式中：J1、J2、J3为偏应力的三个不变化；J2代表塑性变形时有效剪应力大小，表征物体屈服破坏形式。

=s1s2+s2s3+s3s1

(4)

Von Mises 应力是基于剪切应变能的一种等效应力，可定义为

(5)

由公式(4)和(5)可以看出，J2和σeffective具有相同的函数模式，也就是说Von Mises 应力可表征偏应力引起塑性变形导致物体的屈服破坏，因此采用σeffective对物体弹塑性状态的屈服破坏分析更为准确。

2 材料模型及参数

依据某城市地下空间掘进爆破案例，拟建立相似3D数值计算模型，模型总尺寸取长度L=20 m，高度H=20 m，厚度d=2 m。从地表至管道中心4 m厚度为软土层，管道置于软土层中心，软土层下部为约16 m的岩土层，管道直径D=1 m。为了对比爆炸载荷对不同壁厚输气管道的破坏以及安全运行的影响，分别设置4种不同壁厚管道进行对比分析，管壁厚度δ分别取0.02 m、0.04 m、0.06 m、0.08 m。掘进形式采用左右两侧双向同时起爆，其中炮孔深度距地表10 m，孔径φ=40 mm，孔深和堵塞长度分别为2 m和0.5 m，单段最大药量Q=8 kg。炸药和岩体外侧采用位移约束和非反射条件控制，管道与土体、炸药与岩体接触面定义流固耦合算法，为防止管道轴向变形过大，对管道两端采用固体约束控制。岩土体以及管道采用LAGRANGE算法控制，炸药选取流变性的ALE算法控制，具体模型如图1所示。

炸药采用乳化炸药，材料为*MAT-HIGH-EXPLOSIVE-BURN，假定岩体为满足各向同性的弹塑性材料，选用*MAT-PLASTIC-KINEMATIC作为其材料类型；土体选用材料类型为*MAT-SOIL-AND-FOAM。低碳合金钢制管道材料选用*MAT-PLASTIC-KINEMATIC类型，该模型可表征各向同性硬化和随动硬化塑性模型。

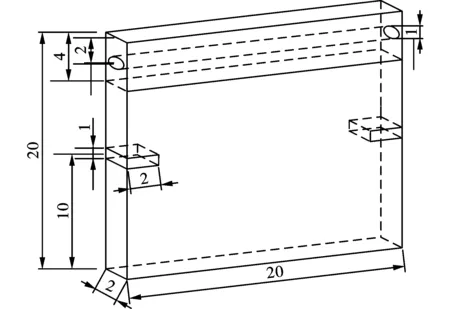
图 1 结构模型(单位：m)Fig.1 Structural model(unit:m)

结合JWL状态方程来表示炸药爆炸过程中压力与体积的关系[16]

(6)

土介质材料选取满足失效准则的模型，要表现出破裂失效还需要添加失效关键字。其屈服应力关系为

(7)

式中，sij为柯西应力张量；P、c为输入常数；β为硬化参数；σ0为屈服应力，MPa；Ep为塑性硬化模量，MPa；ε、εp为应变率、有效塑性应变。见表1、表2、表3。

表 1 炸药参数[17]

P为爆轰压力；V为相对体积；E0为初始比内能；A、B、R1、R2和ω均为描述JWL方程的独立常数。

表 2 岩土体材料参数

ρ为密度；E为弹性模量；G为剪切模量；μ为泊松比；σy为屈服极限；β为岩体硬化系数。

表 3 管道材料参数

ρ为密度；E为弹性模量；μ为泊松比；σy为屈服应力；Etan为剪切模量。

3 爆破载荷作用下输气管道有效应力及振动速度分布

3.1 有效应力分布

定义管道下侧靠近爆源为迎爆面，上侧背离爆源为背爆面，沿管道延伸方向每隔5 m距离取一监测点，从左至右共取5个监测点分别为A、B、C、D、E，具体情况如图2所示。

图 2 监测质点分布情况Fig.2 Locations of the monitoring points

通过上文分析可知，Von Mises 应力σeffective考虑了三个方向的应力变化，并且能够较为准确地反映管道在冲击载荷作用下的塑性变形和屈服破坏形式，因此有必要对管道延伸方向迎背爆面上不同质点的σeffective进行分析。图3为不同时刻壁厚δ=0.02 m的管道上有效应力分布云图。

图 3 不同时刻管道有效应力云图Fig.3 Effective stress nephogram of the pipeline at different times

地震波约t=12 ms时传到管道中并引起管道表面质点有效应力的增加，管壁振动效应逐渐增强。约20～50 ms时刻达到应力峰值状态，其最大值可达0.107 GPa。约t=80 ms以后爆破振动波在管道中传播能量逐渐消失，管壁上有效应力逐渐降低并趋于稳定。对比不同时刻有效应力云图发现，管道背爆面局部应力峰值数值明显高于迎爆面，而文献[4] 中朱斌等人通过对下穿预埋燃气管道的现场爆破试验研究指出管道中心截面为最危险截面，并且截面背爆侧峰值应力大于迎爆侧，该规律与本文数值模拟结果一致。其原因是背爆面上侧为无限大地表，即背爆面上侧存在较大区域的自由面，当应力波穿过背爆面之后，在地表自由面上会形成强烈的反射拉伸波，导致背爆面出现了局部应力放大效应。由于是双爆源起爆，所以接近管道两端处有效应力最大，而管道中心部位最小，其最危险工况接近管道两端位置。该规律与文献[4]正好相反，原因是本文选择两端同时起爆，而文献[4]则是爆源选在管道中心正下方的单爆源起爆方式。由于迎背爆面应力分布存在较大差异，所以有必要对其进一步研究。分别提取4种不同壁厚δ=0.02 m、0.04 m、0.06 m、0.08 m条件下管道迎、背爆面5个监测质点的有效应力随时间变化数值，绘制有效应力时程曲线，如图4、图5所示。

图 4 迎爆面监测质点有效应力时程曲线Fig.4 Time history curve of the effective stresses at the monitoring point on the side of the pipeline towards the blasting source

图 5 背爆面监测质点有效应力时程曲线Fig.5 Time history curve of the effective stresses at the monitoring point on the side of the pipeline away from the blasting source

通过分析发现，无论迎背爆面，都呈现出随管道壁厚增加，有效应力呈衰减趋势，并且呈非线性衰减，文献[8]对不同壁厚条件下管道表面的应力分布进状况行了研究，其分布规律与本文所得结论一致。当管壁厚度增量为Δδ=0.02 m时，迎爆面和背爆面有效应力峰值衰减率分别为κ1=25.2%、19.2%、10.7%和κ2=50%、25%、13.3%，背爆面有效应力峰值衰减率明显高于迎爆面。其主要原因是，壁厚增加的同时增大了振动波波阻抗，使其管道表面受力载荷减弱。在等厚度增加壁厚的情况下，有效应力衰减率逐渐减小，在节约工程成本的情况下，不能无限制增加管道壁厚，其具体壁厚取值范围应控制在某一最佳工程成本的基础上。

3.2 振动速度分布

管道单元受冲击载荷发生非线性振动，振动速度作为一项重要的振动强度因子需要进行监测分析。图6为不同时刻壁厚δ=0.02 m的管道上合速度布云图。

图 6 不同时刻管道质点合速度云图Fig.6 Cloud diagram of the particle resultant velocity of the pipeline at different times

同样分别提取4种不同壁厚δ=0.02 m、0.04 m、0.06 m、0.08 m条件下管道迎、背爆面5个监测质点的合速度随时间变化数值，绘制合速度时程曲线，如图7、8所示。

图 7 迎爆面监测质点合速度时程曲线Fig.7 Time history curve of the resultant velocities at the monitoring point on the side of the pipeline towards the blasting source

图 8 背爆面监测质点合速度时程曲线Fig.8 Time history curve of the resultant velocities at the monitoring point on the side of the pipeline away from the blasting source

通过分析发现，当t=12 ms时，管道表面振动合速度开始上升，也就是说该时间点振动波传至管道，约20～40 ms时刻振动合速度达到峰值状态，最大值可达vmax=2.2 cm/s。同样约t=80 ms时，合速度接近零，趋于稳定态。随着管壁厚度的增加，合速度同样呈现出非线性衰减规律。但值得注意的是，迎爆面振动合速度明显高于背爆面。文献[18]中郑爽英等人采用有限元3D模型对下穿兰成渝输气管道的仙女岩隧道爆破进行数值分析，研究指出管道底部振动速度和位移明显高于管道顶部，与本文所得结论完全吻合。根据《爆破安全规程》规定，若以爆破振动速度作为地表安全判据时，当vmax=2.2 cm/s时，监测值点属于安全状态。无论迎背爆面，都呈现出随管道壁厚增加，合速度呈非线性衰减趋势，并且衰减率逐渐减小。距管道两端1/4处质点合速度值最大。

4 管土耦合模型振速衰减分析

地下空间掘进爆破过程中，由于输气管道深埋地下，故管道振动情况测量存在较大难度，但对于管道上方地表质点的振动情况监测较为方便。通常质点的峰值振动速度vmax可以作为振动大小的主要判据之一，所以有必要对爆点至地表垂直方向质点的vmax传播规律进行研究，该垂直方向vmax的特征点主要是迎爆面、背爆面以及地表处的3个质点。基于4种不同壁厚的管土耦合爆破模型，沿输气管道长度方向分别提取3个特征质点的峰值振动速度vmax，绘制变化曲线，如图9所示。

图 9 耦合模型振动速度峰值曲线Fig.9 Peak vibration velocity curve of the coupling model

通过对图9分析发现，随着管道壁厚的增加，各特征点峰值振动速度逐渐衰弱，其中迎爆面出现最大峰值vmax=2.26 cm/s，而地表质点出现最小峰值vmax=0.142 cm/s。并且由于爆源和管道沿着管线长度的对称性，各特征点的vmax沿长度方向分布规律基本一致。另外建模时未对管体内部添加油气流量，管道中主要成分为空气，空气对振动波的损耗远远小于土体，加之管体迎-背爆面间距小于背爆面到地表的距离，所以vmax在软土层传播过程中衰减更为明显。另外vmax在3个特征点处衰减规律基本一致，管道中心处vmax值最小，而距管两端面1/4处vmax值最大。

对3个特征点vmax的衰减规律进行分析，可获得管土耦合模型的爆破振动效应衰减情况。依据图9的vmax数值，计算出4种不同壁厚的3个特征点峰值振动速度衰减率η。定义振动速度衰减率η=-vi+1/vi，其中i=1,2,3，分别代表迎爆面、背爆面和地表质点。具体如表4所示。

表 4 各质点振动速度峰值衰减率

通过表4计算可得，输气管道壁厚取δ=0.02 m、0.04 m、0.06 m、0.08 m时，迎-背爆面质点峰值振动速度平均衰减率分别为η1=24.6%、18.96%、15.04%和14.78%，而背爆面到地表质点峰值振动速度平均衰减率分别为η2=73.46%、69.4%、66.52%和63.6%。

目前国内外对于爆破振动引起的质点峰值速度半经验公式运用最为广泛的是萨道夫斯基模型[19-20]

(8)

本数值计算模型中，炸药量Q始终未定值，可作为常数项进行处理，依据速度衰减率η=-vi+1/vi公式，可获得迎-背爆面和背爆面-地表质点的峰值振动速度衰减率η1和η2的函数关系

(9)

式中：R1、R2、R3分别为起爆点距迎爆面、背爆面和地表质点的垂直距离;α1、α2为衰减系数。

将表5中计算出的不同壁厚情况下vmax衰减率带入公式(9)，可求得相应的衰减系数α1、α2，具体数据见表5，平均衰减率和衰减系数随管壁厚度变化关系见图10所示。

表 5 各质点振动速度峰值衰减系数

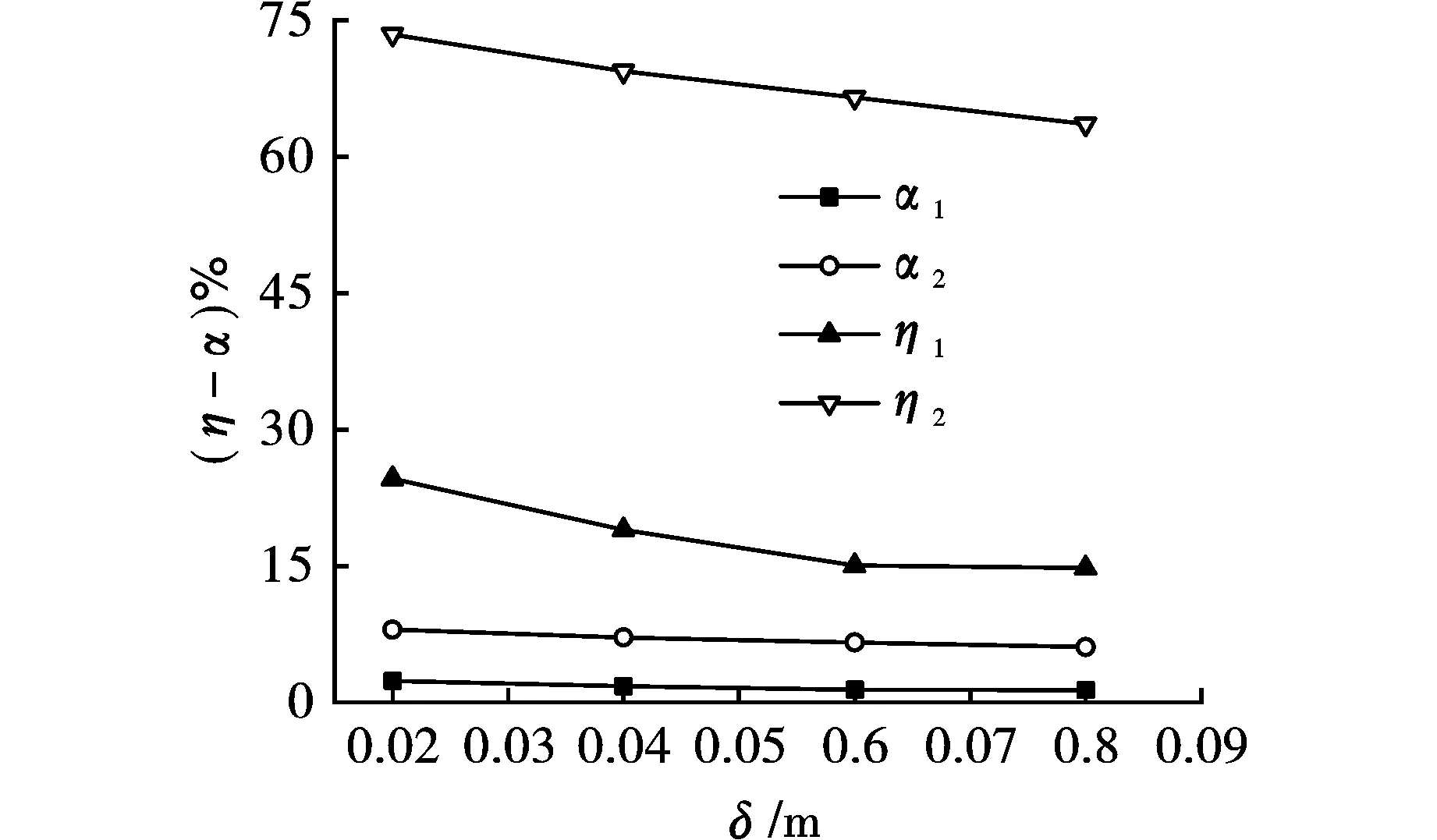
图 10 不同壁厚条件下峰值速度平均衰减率以及衰减系数Fig.10 Average attenuation rate and attenuation coefficient of the peak velocity for different wall thicknesses

5 结论

基于弹塑性理论建立了以岩石-土体-管道流固耦合数值模型，探究了该模型在不同管道壁厚条件下管道动力响应机制，通过计算分析，主要得到以下结论：

(1)城市输气管道在强烈的爆破载荷作用下属于弹塑性力学问题，所以采用塑形变形理论Mises准则对管道屈服模式进行分析更符合实际情况。

(2)在双爆源对称起爆模式下，管道迎-背爆面质点的有效应力和振动速度都随管道壁厚的增减呈非线性衰减趋势，且衰减率逐渐减小。管道背爆面局部应力峰值数值明显高于迎爆面，而迎爆面振动合速度明显高于背爆面。有效应力峰值靠近管道两端，而振动速度峰值对称分布在距管道两端1/4位置处。

(3)当管壁厚度增量为Δδ=0.02 m时，迎-背爆面有效应力峰值衰减率分别为κ1=25.2%、19.2%、10.7%和κ2=50%、25%、13.3%。4种不同壁厚条件下迎-背爆面和背爆面-地表质点峰值振动速度平均衰减率分别为η1=24.6%、18.96%、15.04%、14.78%和η2=73.46%、69.4%、66.52%、63.6%。