复杂充填体对爆破地震波传播特性影响研究*

贾志伟,帅金山，胡 勇

(1.中金黄金股份有限公司，北京100011；2.湖北三鑫金铜股份有限公司，大冶 435100)

伴随着科技的发展，矿山生产规模不断扩大，大直径深孔爆破技术的应用越来越广泛，对爆破振动信号的研究也在逐步深入。通过一定的手段来捕捉和收集爆破产生的振动波信号并对其进行分析和解算，可以有效帮助我们进行爆破振动的研究。在传统的傅里叶法爆破振动信号分析法相比[1,2]，HHT(Hilbert-Huang Transform)分析法是一种创新性的且非常适用于矿山爆破振动波分析方法[3]。伴随着充填采矿法在矿山广泛应用，爆破过程中爆破地震波不可避免会穿越充填体，因此很有必要研究充填体对于爆破地震波的影响。

针对充填体和爆破振动信号HHT分析的问题。赵亮针对振动波的衰减规律[4]，结合动荷载传播理论，通过现场爆破振动实验的手段，得出振动波在矿体和充填体中的衰减系数。袁本胜为了探究爆破振动在安庆铜矿的充填体的衰减规律[5]，通过爆破振动实验和声波测试法的手段，结合分析试验数据得出：充填体破坏区的爆破振动衰减慢。刘宏颖结合实验数据中的充填体内应力和损伤因素的变化情况[6]，分析得出充填体边界失稳很大一部分是因为爆破参数选取得不合理，在爆破参数选取上采取大边孔距。周俊汝通过分析HHT频段曲线的参数信息[7]，得出爆破振动与爆心距存在正比关系，主频会不断衰减，其衰减公式拟合是由于局部振动波传播过程中会出现变动。曹光磊通过使用ANSYS-DYNA软件[8,9]，建立巷道掘进模型并结合动力分析，通过分析单元峰值有效应力结果来反映岩石内部在爆破过程中的应力分布变化。田凯针对如何优化浅埋隧道控制爆破的研究问题[10]，运用ANSYS/LSDYNA进行数值模拟，分析不同爆破方法和装药结构的爆破效果，来确定浅埋隧道爆破优化方案。李强针对巷道、硐室等地下工程的稳定性问题[11]，通过HHT信号解析技术，分析爆破振动信号与频率的关系。宋文峰和魏新江使用HHT分析方法[12,13]，研究了不同爆心距处爆破地震波Hilbert能量及瞬时能量衰减规律。张其虎和曹晓立为了对爆破地震波信号的峰值、频率和振幅等进行了分析[14,15]，通过HHT方法和EMD分解地震波信号，胡刚提出采用HHT理论变换爆破振动信号获取瞬时能量谱[16,17],依据质点振动能量分析隧道围岩结构爆破累积损伤效应的新方法，并且同爆破振速波形面积理论对比,证明该方法的可行性。目前已有研究对于充填体对爆破地震波的影响仍处在较浅的研究阶段。

因此，在湖北三鑫金铜矿的鸡冠咀矿区已充填矿体的基础上进行残矿回采的工程背景下，基于HHT信号分析方法和ANSYS/LSDYNA数值模拟手段，研究回采过程中爆破地震波在穿越充填体前后的各项参数的变化，极具工程指导和应用意义，可以为分析爆破振动效应和如何减少爆破振动危害提供理论依据，为后续矿山爆破优化提供技术帮助。

1 爆破振动测试

1.1 测试方案

论文以湖北三鑫金铜矿为工程研究背景，矿井采取充填开采方法，按采一隔一的要求分步进行回采，结束后再进行充填。在每个中段之间留有10 m厚的顶底柱作为支护，顶底柱共分为两层，每层高4 m，上部由2 m高的矿体来护顶。如图1所示。因此，在回采间柱时，矿房的两边都出露在充填体两侧。矿井充填骨料来自于选矿厂分级处理的粗尾砂，胶结材料经过反复试验和优选，目前利用新型尾砂胶结材料来替代高水材料和普通混凝土及各种充填材料。新型尾砂胶结材料不仅费用低、水化物稳定、胶结强度高而且还有用量低、早期强度高等优点。

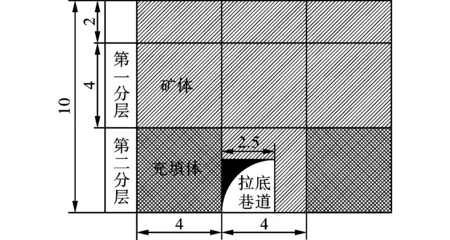
图 1 回采方案示意图(单位：m)Fig. 1 Schematic diagram of stoping(unit:m)

为了研究爆破地震波经过复杂充填体后的变化规律，明确复杂充填体对爆破地震波传播特性的影响。开展爆破测振试验的主要目的是为了采集爆破振动原始信号并为优化爆破设计方案提供相关重要参数。本次测振设备选型为TC-4850型号，共两台，监测点位和设备布设范围均位于鸡冠咀矿区的-370 m中段中。其中号传感器布设矿房内，号传感器布设在间隔充填体的相邻矿房内。布设传感器时尽量使爆源与传感器在同一直线上，测点布设情况如图2所示。

图 2 测振方案示意图Fig. 2 Schematic diagram of vibration measurement plan

1.2 测试数据

爆破地震波先经过号监测点最后到达号监测点。测点的现场实际监测结果共两组爆破振动信号数据，测得三向的振动的速度和主频，见表1。

2 HHT信号分析技术

(1)EMD分解

经验模态分解(Empirical Mode Decomposition，EMD)是基于数据本身的时间尺度特征，没有预先设定任何基函数的一种时频域的信号处理方法。在处理非平稳和非线性数据方面，EMD具有明显优势，同时在分析非线性和非平稳信号序列方面尤为适用，在通信质量上具有可靠性。该方法的关键是经验模态分解，它把复杂信号分解为有限个固有模态分量(IMF)和一个余项。

表 1 三向振动监测数据统计表

为了得到有意义的瞬时频率，需要让函数是对称的，局部均值为零，并且过零点和极值点的数目必须是相等的。信号是由数个本征函数组成的，单个函数必须满意下面两个前提条件：一是在函数的全部时间维度上，局部极值点和过零点的个数必须相同或最多相差一个；二是在任意时间点上，局部最大值的上包络线和局部最小值的下包络线的均值必须为零。

EMD将输入信号分解为若干个本征模态函数和一个残差，由以下公式组成

式中：f(n)表示输入信号；IMFm(n)表示Mth的本征模函数；ResM(n)表示残差。

EMD分解过程提取的过程叫作筛选，具体过程如下：

(1)标出局部极值点。

(2)通过三次样条插值连接极小值点构成下包络线，连接极大值点构成上包络线。

(3)求上下包络线的均值m1。

求出上下包络线均值，同时用输入信号减去该数值

X(t)-m1=h1X(t)-m1=h1

上述过程的一次迭代不能保证h1是本征模函数(IMF)，需要重复上述过程，直到h1是本征模函数(IMF)。

(2)HHT变换

当T(t)和H(t)形成大小相同，角度相反的两个复数时即可得到一个分解信号

P(t)=T(t)+jH(t)=b(t)ejα(t)

其中

由上式可求解出振幅与时频之间的相互关系，进而对希尔伯特谱对时间进行积分求解出边际谱

瞬时能量谱的计算方式是把振幅的平方对频率积分

3 穿越充填体爆破振动HHT分析

3.1 EMD分解

该矿山的爆破地震波的传播特性与充填体有着非常密切的关系，因此研究充填体对爆破地震波的传播影响十分有必要。爆破振动信号能量随时间频率变化的研究在地震波穿越充填体传播特性的研究中起着非常重要的作用。由于地震波的传播方式分为三种类型，包括切向、径向和垂直方向，所以在工程爆破中，对三维信号进行监测。在一些西方国家中，以质点竖直方向的振速峰值来作为爆破振动强度的指标。而垂直方向又具有很强的典型性，因此爆破振动信号选用第一组数据的竖直方向(Z方向)的分量作为分析对象，其原始波形如图3所示。

图 3 爆破振动原始信号图Fig. 3 Blasting vibration waveforms

如图4所示，原始信号在穿越充填体之前和之后通过EMD分解分别产生了IMF分量16个和15个。EMD的分解规律是从高频至低频，剩下一个为残差IMF。基底函数在EMD分解中没有单一的，是由信号的自身特征设定的每个IMF分量的提取，这就是它的适应性，让信号分析拥有很大的通用性和多功能性。与此不同的是，替代性分析方法如小波和傅里叶，必须先行设置基底函数，基底函数自身就有一定的局限性，因此各种结果的选择并不对等，一般来说甚至有很大的区别，此外还不可避免地引入了频率扩散。

IMF分量是由EMD分解出来的，且大都拥有明确的物理意义。从穿越充填体前IMF分量图来看，第一个至最后一个的IMF分量的频率逐步降低，表明在爆破地震波的整个传播过程中，大幅度衰减是高频部分，但第二个至第五个IMF分量的振幅较第一个IMF分量的振幅大跨度增加，并且信号的大部分能量都被其包括，它属于原始信号的优势频段。此外，第十四个至第十六个IMF分量是分解后频率更小的部分，这可能是信号本身原有的或由不同情况产生的。最后一个IMF代表着爆破测振仪的散失抑或是测振信号微弱的衰减趋向。这意味着EMD方法是一种新型的主成分分析方法，它可以提取信号本身原有的由高到低的所有模态函数，并分解出许多IMF分量，整合了原始信号中最重要的信息。同理，从穿越充填体后IMF分量图来看，第一个至第十二个IMF分量是进行研究的主要对象，它几乎囊括了爆破振动信号的全部能量，在爆破振动信号中属于主导的振动频率，又称为优势频率。最后一个IMF并没有有用的分析价值和意义，可以被忽略。由于重建的信号波能排出干扰因素，更符合和便于研究爆破振动波的真实特性规律，因此，将穿越充填体前的IMF分量去掉第十四、十五和十六个IMF分量和穿越充填体后的IMF分量去掉第十三、十四和十五个IMF分量，进行爆破振动数据EMD重构，以便后续的HHT频谱分析。见图5。

多机器人协同系统在汽车焊接生产线中的应 用 …………………………………………… 钟 平，李华雄（31）

3.2 HHT频谱分析

爆破振动信号处理后再进行希尔伯特变换得到边际谱分析图和瞬时能量图，利用相应图谱对分析对比爆破振动信号。

穿越充填体前后边际谱图(图6)将直观地分析爆破振动信号的各个频率组成，并准确地反映每个频率部分的能量振幅。从穿越充填体前边际谱图中可以得出，爆破振动频率在穿越充填体前重点聚集在60～80 Hz，累计能量范围为0.3×10-4～0.2×10-6；爆破振动信号经过充填体后边际谐波峰减少，子频带变多，穿越充填体后爆破振动频率主要集中在50～60 Hz，积累的能量范围变为0.2×10-6～0.7×10-5，但是低频能量占比增加，穿越充填体后高频频带60～80 Hz积累的能量范围比穿越充填体前衰减了7倍，能量分布更加扩散。

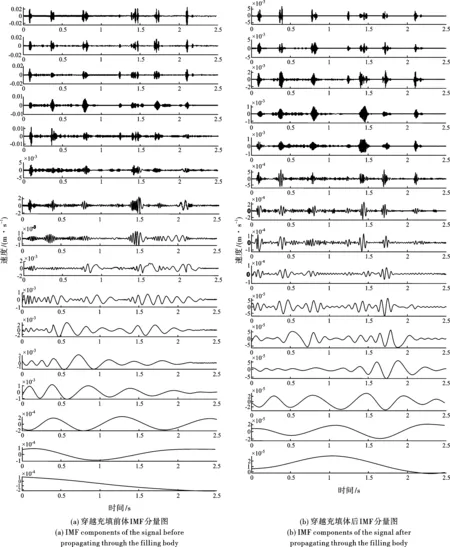
图 4 爆破地震波振动信号EMD分解结果图Fig. 4 EMD decomposition of blasting vibration signal

从穿越充填体前爆破振动信号瞬时能量图中(图7)分析得出，能量随时间的变化表明，这是由导爆管引起的爆破结果，图中波峰起伏高点处瞬时能量强烈，穿越充填体前后的波形信号起伏变化都在0.10～2.20 s的区域内，且爆破延期间隔时间为在0.2～0.4 s区域内，表明单段装药爆破产生的爆轰高压气体在裂隙和炮孔可维持在0.2～0.4 s区域内，均大于60 ms，这十分有利于破碎岩石。

穿越充填体前的爆破振动信号达到瞬时能量最高点处时间为1.50 s左右，此处最大的瞬时能量约为2.4×10-3。穿越充填体后瞬时能量达到最大值的时间在0.40 s左右，此处最大的瞬时能量约为0.9×10-4。将两组信息进行比对得出，穿越充填体前的最大瞬时能量是穿越充填体后最大瞬时能量的27倍左右。

图 5 EMD重构信号图Fig. 5 EMD reconstruction of signals

图 6 边际谱图Fig. 6 Marginal spectra

图 7 瞬时能量图Fig. 7 Instantaneous energy spectra

4 穿越充填体爆破振动数值模拟分析

4.1 炸药模型

基于数值模拟中有限元法，采用LS-DYNA，模拟炸药能量对岩体的变形影响和起爆后冲击波在围岩中的传播形式，尤其针对充填体中的质点在爆破冲击波作用下的振速规律。本次模拟采用的高能燃烧模型是根据药包内各点距爆源点的距离和爆速来计算起爆时间。

PS=Ae-R1V+Be-R2V+CV-(ω+1)

式中：V=v/v0=ρ0/σ为相对比容，即现时比容v与初始比容v0之比，A、B、C、R1、R2、ω为材料参数，根据所用炸药取参。

4.2 矿体和充填体力学模型

为便于计算，保证模拟结果的唯一性，将矿体和围岩简化为弹塑性体，用双线性随动硬化模型计算，并采用Mohr-Coulomb屈服准则。

4.3 材料参数的选取

在本文中所选用的是乳化炸药，根据4.1节所述，其详细材料参数见表2。表3和表4记录了矿体和充填体的物理力学参数。

表 2 炸药参数

表 3 矿体力学参数

表 4 充填体力学参数

4.4 数值模型的建立与边界条件

构建了尺寸为28 m×20 m×12 m的数值网格模型。该模型可视为四周存在岩体，模型的边界条件受模型外岩体影响，但由于模型尺寸相对于爆破应力波传播距离较大，应力波对边界处质点的状态影响较小，可忽略不计，因此立方体模型六个面的边界条件设为位移约束。

图 8 网格划分图Fig. 8 Numerical model and meshing diagram

4.5 结果分析

将4.4节所述模型导入软件并根据4.3节所述参数进行赋值并求解。根据现场装药参数和测点布置情况，选取现场和号测点中模型对应的位置作为分析测点，分别对应A和B测点。两个测点在垂直(Z轴)方向上的爆破振动速度变化如图9所示。

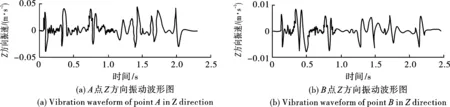
图 9 监测点Z方向振动波形图Fig. 9 Vibration waveforms in Z direction at the monitoring points

根据数值模拟结果可知，A和B测点处的Z方向爆破振动质点峰值速度为4.8 cm/s和0.8 cm/s，与矿山实测的爆破振速相接近，说明该数值模拟能够一定程度上解释爆破结果，分析复杂充填体对爆破地震波传播的影响。

图10是监测点的有效应力曲线示意图，该图反应了岩体的应力变化特性。图10显示了A和B点的最大有效应力。从图10可以看出，记录单元A和B点的最大有效应力为35 MPa和30 MPa，爆破地震波的传播经过充填体后，监测点最大有效应力下降14%。

此外，两监测点的最大有效应力均小于采场的岩体最大动态抗拉强度40 MPa[18]，表明A和B监测点采场区域在爆破振动的影响下较为稳定。

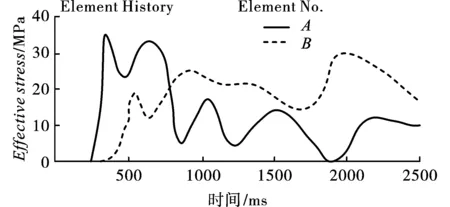
图 10 监测点最大有效应力示意图Fig. 10 Maximum effective stresses at the monitoring points

5 结论

利用HHT信号分析技术，对穿越复杂充填体前后的岩体进行爆破地震波信号分析，揭示了爆破振动信号在穿越充填体前后的变化规律。采用数值模拟手段分析了爆破地震波穿越充填体前后岩体的最大主应力变化，并得到相应结论：

(1)穿越充填体前和穿越充填体后的爆破振动主频分别为60～80 Hz和50～60 Hz，表明该充填体对爆破地震波具有过滤高频的作用且往低频方向发展，且穿越充填体后高频频带60～80 Hz积累的能量范围比穿越充填体前衰减了7倍，能量分布更加扩散。

(2)穿越充填体前后的波形信号起伏变化都在0.10～2.20 s的区域内，穿越充填体前的最大瞬时能量是穿越充填体后的27倍左右，说明爆破地震波穿越充填体后峰值能量得到大幅度衰减。穿越充填体前后的波形信号起伏变化都在0.10～2.20 s的区域内，且爆破延期间隔时间为在0.2～0.4 s区域内，表明单段装药爆破产生的爆轰高压气体在裂隙和炮孔可维持在0.2～0.4 s区域内，均大于60 ms，这十分有利于破碎岩石。

(3)根据数值模拟结果，爆破地震波的传播经过充填体后，使得监测点处的最大有效应力下降了14%左右，且监测点位最大有效应力均小于采场的最大动态抗拉强度40 MPa，说明监测点采场区域在爆破振动的影响下较为稳定。