钢筋混凝土楼房双向折叠爆破设计方法*

2022-09-20孙金山谢先启贾永胜姚颖康

爆破 2022年3期

孙金山，谢先启，贾永胜，姚颖康

(江汉大学 a.省部共建精细爆破国家重点实验室；b.爆破工程湖北省重点实验室，武汉 430023)

目前，高层和超高层楼房的拆除主要采用控制爆破技术[1,2]。随着建筑结构日益复杂以及建筑密度的不断增加，拆除爆破的技术难度日益加大，应用条件也日益苛刻。为此，高层建筑物的爆破拆除过程必须进行严格和精密的控制。建筑物的控制爆破拆除技术兴起于20世纪50年代，工程应用至今仍十分活跃。该技术利用炸药爆炸能量破坏建筑物的关键受力构件，使之失去承载能力，并通过合理的设计控制建筑的倒塌方向、破坏范围、破碎程度和爆破有害效应等[3-7]。

近年来，国内爆破行业逐渐推广采用双向折叠爆破技术拆除一些倒塌空间不足的高大结构，该技术将高耸建筑分成几段，使其在倒塌过程中发生折叠，并且该技术也开始在国外推广应用(图1b)。2004年，武汉首次成功采用双向折叠爆破技术拆除了一座100 m高的钢筋混凝土烟囱[8,9]。2007年，拆除了一座19层的楼房[10]。2019年，拆除了一座14层框剪结构楼房[11]。近年来，该技术已在大量拆除工程中得到应用[12,13]。在近二十年来，虽然折叠式爆破技术在许多工程中得到了应用，但由于缺乏设计标准，一些工程的爆破效果并不理想[14]。为此，介绍了双向折叠爆破拆除技术的基本原理，提出了双向折叠爆破拆除技术的设计准则和主要参数的理论选取方法，并通过工程实例进行了验证。

图 1 烟囱和建筑物的折叠爆破拆除Fig. 1 Fold implosions of chimney and building

1 关键参数设计

与传统的拆除爆破模式类似，折叠爆破方案设计过程中也需要确定合理的总体方案以及爆破位置、炮孔及装药参数、起爆网路等，此外，还需要确定爆破切口的数量、开口方向、高度位置。

1.1 爆破切口数量与方向

采用双向折叠爆破时，应在楼房的特定高度上布置2～3个楔形爆破切口(图2)。在爆破切口中，大部分的柱和剪力墙应被破坏，使切口区残余的柱和墙形成“塑性铰链”，爆破的楼房则变成一个折叠的运动链。因此在爆破方案设计过程中，应该首先设计爆破切口的数量、位置和方向。

切口的数量控制楼房的倒塌范围，但过多的切口也不利于倒塌过程的控制，将增加倒塌失控的风险。为了降低成本和提高效率，两个切口间楼房分段的高度Hi应大于其宽度W的两倍，即

Hi>2W

(1)

式中:Hi为折叠分段高度；W为分段的宽度(平行于倾倒方向的剖面)。

图 2 折叠爆破示意图Fig. 2 Diagram of fold implosion

为确保折叠运动的稳定性，各楼段的惯性矩应大致相等，所以每个分段的重量应大致相等

m1≈m2…≈mn

(2)

式中，mn为折叠分段质量。

根据公式(1)和公式(2)可以确定爆破切口的数量。

其次，要实现可靠的折叠过程，应使相邻爆破切口的开口方向相反。因为倒塌范围主要受底部爆破切口的控制。所以底部切口的开口方向应朝向倒塌范围最充裕的方向。

1.2 爆破切口起爆顺序

爆破切口的起爆顺序主要有两种模式：自上而下和自下而上。采用自上到下顺序时，爆破切口的塑性铰更易形成，且上切口的闭合对下段的运动影响较小(图3a)。采用从下到上顺序时，上部切口处重力力矩在楼房转动过程中会变得很小，导致切口塑性铰的形成较困难，爆破方案的可靠性将降低(图3b)。因此，建议爆破切口采用自上而下的起爆顺序。

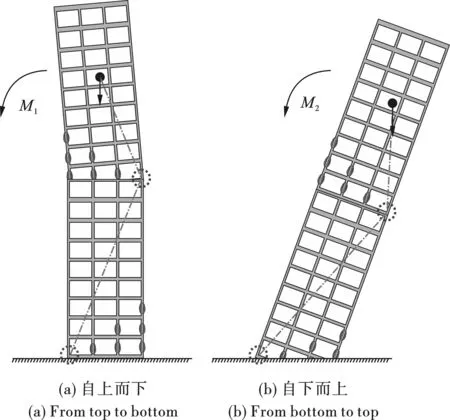
图 3 不同起爆顺序示意图Fig.3 Diagram of initiation sequence of notches

1.3 爆破切口起爆时差

爆破切口间的起爆时差对折叠运动姿态影响很大，因此确定起爆时差时应遵循以下准则。

(1)要使楼房从结构转化理想的运动机构，需使爆破切口能形成塑性铰链，而其形成过程需要足够的时间，因此相邻切口的最小起爆时差等于理想铰链旋转1°～2°所需的时间

Δt≥Δtmin=Δt|Δθ=1°～2°

(3)

式中，Δθ为起爆后切口上方楼房分段旋转的角度。

(2)爆破切口最终将闭合，且其闭合时的强烈碰撞可能会使折叠运动变得难以控制。因此，相邻爆破切口的最大起爆时差应等于爆破切口闭合所用的时间

Δt≤Δtmax=Δt|Δθ=Φ

(4)

式中，Φ楔形爆破切口的张开角度(如图2所示)。

(3)在双向折叠爆破运动过程中切口闭合时，应确保楼房在空中的运动姿态呈Z字形。

(4)为确保楼房安全地倒塌，须确保其下段先落地，上段后落地，且下段落地时上下段之间的夹角必须小于90°。

2 折叠塌落过程计算模型

由公式(1)～(4)可以获得无数组关键参数的组合，而为了确定最优的参数组合，必须对设计方案的折叠运动状态进行预测和评估。爆破切口闭合前折叠运动是与理想运动过程接近，因此，可以采用多体动力学模型来预测早期的倒塌过程。

2.1 两次折叠运动

两次双向折叠爆破需在楼房的底部和中部设置两个切口，是最简单的折叠方案。采用三次折叠时上两段也需经历两次折叠的阶段。两次折叠倒塌过程可以分为两个阶段(如图4所示)：阶段(1)是从上部切口(t=0)的起爆到下切口的起爆(t=t1)的过程；阶段(2)是下切口起爆之后的过程。

在阶段(1)中，根据牛顿运动定律，上段运动方程可表示为

(5)

式中：J1是上段的转动惯量(旋转轴是上部塑性铰链)；r1是上段质心到上部塑性铰链的距离；θ1是r1与垂直轴的夹角；m1是上段的质量；g是重力加速度。

公式(5)的边界条件为

式中：θ10是θ1的初始角；t=0是上切口的起爆时间；θ′1是角速度。

在阶段(2)中，下段开始旋转。在笛卡尔坐标系下，上段质心坐标可表示为

(6)

式中：x1、y1分别为上段质心的横坐标和纵坐标；L2为下切口转动轴与上切口转动轴之间的距离；θ2为r2与垂直轴之间的夹角(顺时针为正，逆时针为负)。

因此，系统的动能E表示为

(7)

式中：J1c为上段的转动惯量(转动轴为其自身的质心)；J2为下段的转动惯量(转动轴为下切口转动轴)；x′1表示x1(t)对时间t的一阶导数，依次类推。

图 4 双向折叠爆破模式Fig. 4 Bidirectional folding implosion mode

以地面为零势能面，系统的势能U表示为

U=m1gy1+m2gy2

(8)

可建立运动系统的拉格朗日方程组为

(9)

解方程(9)，可得微分方程组为

(10)

方程组(10)的边界条件为

θ1|t=t1=θ1，t1,θ2|t=t1=θ2，t1,

θ′1|t=t1=ω1，t1,θ′2|t=t1=0

式中：θ1，t1和θ2，t1是下切口起爆(t=t1)时θ1和θ2的角度；ω1，t1是t=t1时刻上段转动的角速度。

设τ=t-t1，可将式(10)的边界条件转化为

θ1|τ=0=θ1，t1,θ2|τ=0=θ2，t1,

θ′1|τ=0=ω1，t1,θ′2|τ=0=0

根据式(10)的解，可以求解θ1(τ)和θ2(τ)，可以得到阶段(2)中楼房任意时刻的运动姿态。

由式(5)和式(10)可分两步模拟双向折叠爆破方案。阶段(1)中，在上部切口起爆后，以初始状态参数为边界条件，求解方程(5)。阶段(2)中，下切口起爆后，以上段的运动状态和下段的初始状态为边界条件，求解方程(10)。方程(5)和(10)虽忽略了爆破荷载、碰撞、摩擦、阻尼等因素，但仍可为运动状态的模拟提供重要的依据。

2.2 三次折叠运动

三次折叠爆破方案在楼房上布置三个爆破切口将其上段，中段和下段(如图5)。其倒塌过程可以分为3个阶段：阶段(1)为从上部切口的起爆到中间切口起爆的塌落过程(0～t1)；阶段(2)是中间切口起爆到下切口起爆的塌落过程(t1～t2)；阶段(3)是下切口的起爆后的塌落阶段(>t2)。

三次折叠爆破过程中，由于采用自上而下的切口起爆顺序，因此其阶段(1)和阶段(2)与2.1节中两次折叠过程一致，应通过方程(5)和(10)进行求解，阶段(3)则通过以下过程进行求解。

在阶段(3)中，上段的质心坐标表示为

(11)

中段的质心坐标表示为

(12)

式(11)和(12)中，x1,y1,x2,y2,r1,r2,L2,L3,θ2,θ3等数学符号和字符的定义如图5所示。

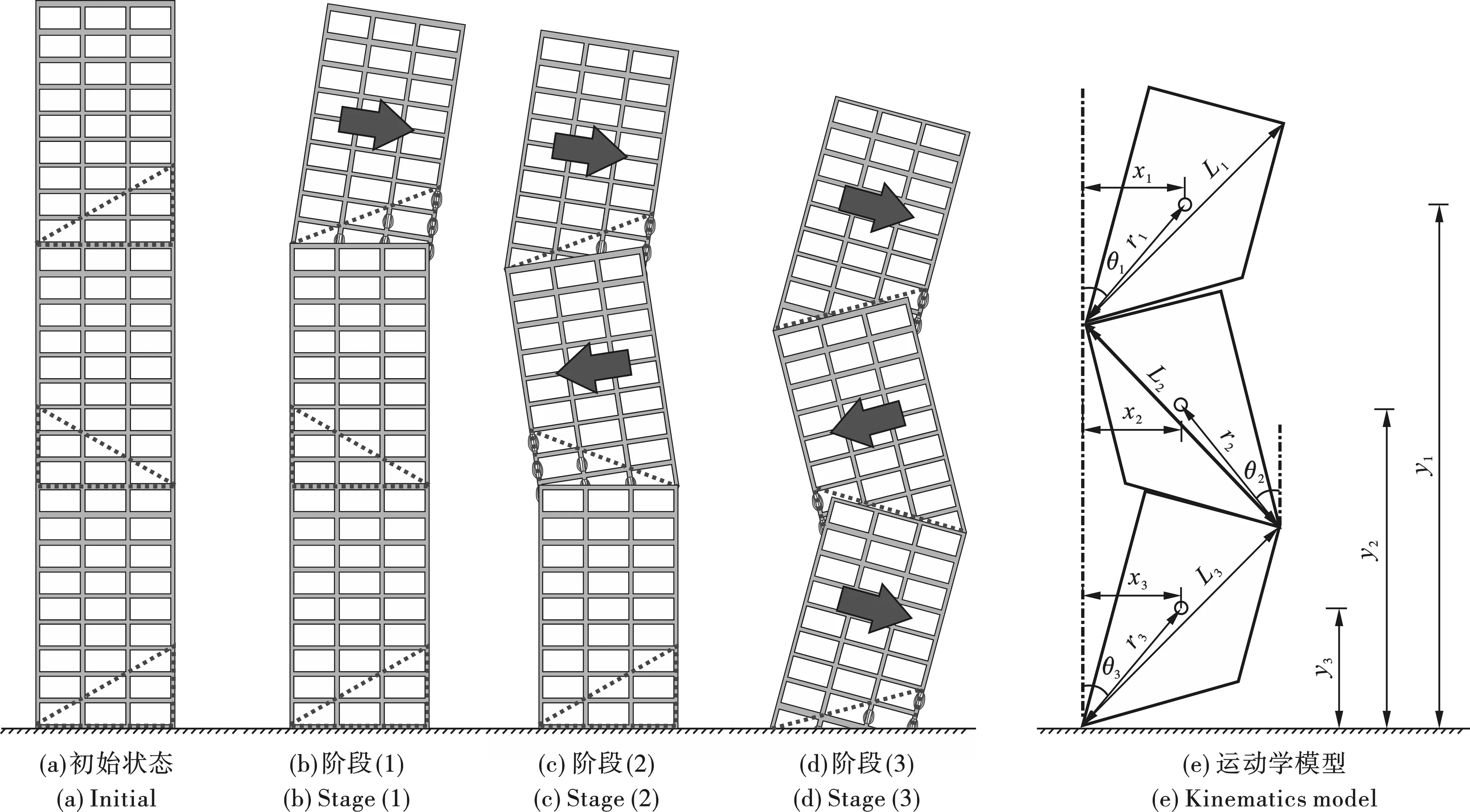
图 5 三向折叠爆破模式Fig. 5 Tri-folding implosion mode

三段运动系统的动能E为

J1cθ′21+J2cθ′22+J3cθ′23]

(13)

式中：J1c、J2c为上段和中段的转动惯量(转动轴为其自身的质心)；J3为下段的转动惯量(转动轴为下切口转动轴)。

以地面为零势能面，势能U表示为

U=m1gy1+m2gy2+m3gy3

(14)

式中：m1、m2、m3为各段质量；g是重力加速度。

建立运动系统的拉格朗日方程组为

(15)

解方程(15)，可得阶段(3)中θ1(t)、θ2(t)和θ3(t)的微分方程组为

(16)

式中：s1=sinθ1;s2=sinθ2;s3=sinθ3;s12=sin(θ1-θ2);s13=sin(θ1-θ3);s23=sin(θ2-θ3);c12=cos(θ1-θ2);c13=cos(θ1-θ3);c23=cos(θ2-θ3)。

式(16)的边界条件为

θ1|t=t2=θ1，t2,θ2|t=t2=θ2，t2,θ3|t=t2=θ3，t2,

θ′1|t=t2=ω1，t2,θ′2|t=t2=ω2，t2,θ′3|t=t2=0

各参数代表的意义与2.1节中相似。

设T=t-t2，将式(16)的边界条件转化为

θ1|T=0=θ1，t2,θ2|T=0=θ2，t2,θ3|T=0=θ3，t2,

θ′1|T=0=ω1，t2,θ′2|T=0=ω2，t2,θ′3|T=0=0

依次求解解方程(5)、(10)、(16)可得阶段(1)、(2)、(3)的θ1、θ2、θ3，进而评价不同参数组合下爆破楼房在不同时刻的塌落姿态，进而确定最佳的方案。

3 工程案例

2007年爆破拆除的武汉中央商务区一楼房，高19层，为框架-剪力墙结构。部分结构参数如表1所示。混凝土强度为30 MPa，钢筋强度为300 MPa。为了对比双向折叠爆破技术和定向爆破技术，将大楼分成两部分，左侧部分采用折叠爆破方案，右侧部分采用定向倾倒爆破方案(如图6)。

图 6 19层建筑三叠爆破拆除方案(单位：m)Fig. 6 Tri-folding implosion plan for the 19-story building(unit:m)

表 1 建筑参数(左侧部分)

根据折叠爆破关键参数设计准则，楼房的左侧部分设置了三个楔形爆破切口，切口位置和参数如表2所示，各切口方向如图6所示，各分段的主要参数如表3所示。根据第1节和公式(5)计算得到，相邻爆破切口之间起爆时差选择范围为0.5～2.0 s。爆破方案设计时，分别选取了多种起爆时差组合进行了分析，部分参数组合如表4所示。