平面P波入射具有不完美界面圆形夹塞的动态响应特性*

2022-09-20李夕兵

爆破 2022年3期

陶明,姚靖,李夕兵

(中南大学资源与安全工程学院,长沙 410083)

在采矿、交通、国防等诸多领域,常常遇到地下构筑物遭受动态扰动而发生损害的问题[1]。扰动的来源既有人为因素也有自然因素,例如钻爆法产生的爆破震动、地震产生的地震波等。这些扰动在地下岩层中以应力波的形式传播,当波遇到不连续面的时候,波的传播状态发生改变并且发生散射。研究表明动态扰动在不连续界面发生散射并引起动应力集中是造成地下构筑物破坏的重要原因[2]。

应力波在传播过程中遇到结构或材料的不连续处将产生应力波的散射,应力集中现象最早由Rankine于1843年发现。1962年鲍亦兴利用波函数展开法研究稳态波入射无限弹性薄板中圆孔的动应力集中问题[3]。刘殿魁等将弹性力学中求解空洞周边静应力集中问题的复变函数论方法推广到SH波入射空洞导致动应力集中问题[4],给出了逼近任意形状孔洞的稳态弹性动力学问题的完备函数序列“域函数”及边界条件的一般表达式。Li,et al用复变函数法求解了瞬态P波作用下浅埋圆形空腔周围的动应力集中情况[5],给出了空腔深度、入射角和波峰位置对动应力集中因子(DSCF)分布的影响。赵春香等研究了SH波入射作用下半空间界面圆孔的动力响应[6],给出了该问题的解析解和动应力分布规律。陈涛等研究了板的横截面处孔洞在平面P波入射下动应力集中问题[7],并得出自由表面距孔洞距离影响动应力集中。除了圆形截面的散射体外,陈志刚等研究了平面SH波在弹性半空间中浅埋椭圆柱形孔洞上的散射[8],结果表明浅埋孔洞与水平表面存在强烈的相互作用并产生动应力集中。Ghafarollahi,et al基于多极展开法分析了SH波以任意角度入射到椭圆形截面空腔或裂缝时的反平面散射问题[9],结果表明入射波数、入射波角、空腔到双材料界面的距离等参数对围岩的动力响应有显著的影响。Tao,et al采用波函数展开法求解了SH波作用下的全平面椭圆空腔周围的散射和动应力集中问题[10],结果表明：入射波、波数、和椭圆轴比对动应力集中有较大影响。

脱胎于实际工程中的波散射问题,边界更加复杂。Lee 等人利用大圆弧假定方法求解了半平面空间中衬砌隧道在P波和SV波作用下的动力响应[11,12],易长平等人使用波动函数展开法来分析衬砌隧道周边在平面波和圆柱波作用下的动力响应[12]。结果表明：衬砌结构刚度的增加将导致隧道围岩的DSCF减小。袁晓铭采用波函数展开方法给出了半空间中圆形夹塞物对平面SH波散射的封闭解析解[13]。Trifunac研究了在入射平面SH波的情况下[14],半圆柱形冲积河谷内及其周围地表运动的性质,并且分析了波入射角度对表面振动特性的影响。刘中宪等基于Biot理论[15],采用间接边界积分方程法,研究流体饱和半空间中夹塞物对平面SV波的二维散射。张鸿等采用饱和土Biot理论分析了地震P波作用下饱和土体中圆形隧洞衬砌的动力响应问题[16]。何颖等采用波函数展开法及边界离散的方法给出了任意断面形状的地下夹塞对平面SH波散射的半解析解[17]。杨在林等采用Green函数,复变函数和多极坐标等方法研究了圆形夹塞和裂纹组合对SH波的散射与地震动[18],讨论各种参数对夹塞上方地表位移的影响。张海等根据弹性波动理论,结合分区和契合思想[19],利用傅里叶级数展开法,由连续性条件和自由地表边界条件,求得了凸起地形中衬砌隧道对SH波散射的解析解。齐辉等对稳态SH(shear horizontal)导波在表面含有多个半圆柱形凹陷的弹性带形介质内的散射问题进行了研究[20],并给出了解析解。

在以往的研究中,夹塞与介质的交界面被认为是完美界面,也就是说位移和应力在界面处保持连续,这在一定情况下是合理的。但是更多情况下,因为裂隙或者是脱胶的原因,界面出现缺陷变为不完美界面。此时,继续假设位移和应力在交界面连续是不合理的。因此引入弹簧模型来表征不完美界面,并且分析不完美界面以及入射波波数对P波入射夹塞动态响应的影响。

1 控制方程

对于动荷载作用下圆柱形夹塞的动态响应,可以将问题简化为平面应力问题。考虑无限均匀弹性介质中有一个无限长圆柱体夹塞,夹塞中心位于o处,如图1。弹性波在传播方向上遇到圆形夹塞,会在夹塞周围发生散射和透射。散射波与入射波在夹塞周边介质中叠加造成夹塞周边动应力集中。以圆形夹塞中心为原点建立极坐标系(r,θ),P波入射方向为x+方向。

在不考虑体力及自由传播情况下,标量波动方程以及入射波表达式见式(1)和式(2)

(1)

u(i)=u0eiαr cos θe-iωt

(2)

图 1 几何模型Fig. 1 Geometric model

平面P波入射并且在圆形夹塞周边发生散射,向介质反射P波和S波,同时,在夹塞中产生驻波。利用Fourier级数将入射波表达式(2)进行展开后根据Bessel函数的积分定义有

(3)

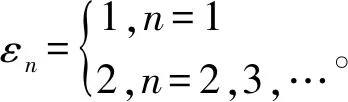
介质中的散射P波、S波位移势函数分别表示为

(4)

(5)

式中：An和Bn为未知系数；α1和β1分别为介质中的P波波数和S波波数。弹性夹塞中的驻波分别可以表示为

(6)

(7)

式中：Cn和Dn为未知系数；α2和β2分别为夹塞中的P波波数和S波波数。将所有波的分量相加,得到介质中总波场

(8)

以及夹塞中波场

(9)

2 边界条件

大多数情况下,考虑波入射夹塞发生散射问题时,假设介质与夹塞交界面为完美界面是合理的。但是在某些情况下,交界面的连接键并不是完全固定和刚性的,而是具有明显的粘弹性[21]。这种不完美界面条件假设在介质和夹塞之间有一层厚度无穷小的无惯性粘弹性层。不完美界面的无惯性表明交界面处的应力连续,粘弹性表明剪切应力与法向应力和各自位移成正比[22],表达式如下

(10)

式中：kr和kθ分别为法向弹簧系数和切向弹簧系数,而下标1和2分别代表介质和夹塞中的参数。

当kr→+∞和kθ→+∞时,界面处的法向位移和切向位移可以看作是连续的,弹簧模型接近于一个完美的结合界面。对于kr→+∞和kθ→0,相当于无摩擦的完美滑移。对于kr→0和kθ→0,也就意味着没有波从岩体传输到夹塞。

3 介质和夹塞中的应力和位移

介质中的应力表达式

(11)

介质中的位移表达式

(12)

弹性夹塞中的应力表达式

(13)

弹性夹塞中的位移表达式

(14)

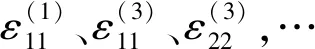
将得到的应力和位移表达式(11)、(12)、(14)代入边界连续条(10),得到求解系数An、Bn、Cn、Dn的联立方程组,用矩阵表示为

QMT=PT

式中：Q为矩阵；M、P为向量。

在没有不连续体的情况下,波在介质中自由传播导致的应力可以表示为

σ0=-α2(λ+2μ)φ0

(15)

根据应力表达式(11)和式(15)可以求得稳态应力集中因子

(16)

4 稳态响应分析

动应力集中因子(DSCF)是评判动应力集中的重要标准。研究问题是不完美界面条件下波入射夹塞的动态响应,给出不完界面条件下的DSCF。计算波在夹塞处的动态响应还需给出具体的材料参数,比如岩石材料,假设参数为：介质与夹塞剪切弹性模量之比为2.5,介质与夹塞波速度之比为1.5,介质与夹塞泊松比分别为v1=0.20,v2=0.25。为了计算更加简便,取kr与kθ的值为m0μ1/a,m0为指定常数。已有的研究表明夹塞周围切向应力远大于径向应力,因此下面仅讨论切向DSCF。

稳态DSCF计算结果如图2所示,为了得到不完美界面对DSCF的影响,分别给出了当kr、kθ→+∞,kr=kθ=10.0μ1/a,kr=kθ=1.0μ1/a,kr=kθ=0.1μ1/a时夹塞周边DSCF分布,其中弹簧刚度趋近+∞代表界面为完美边界条件。图2(a)显示无量纲波数为0.25,此时弹簧刚度对DSCF的影响十分明显,当kr=kθ=0.1μ1/a时DSCF峰值出现在θ=π/2为4.045,是完美界面DSCF峰值2.624的1.54倍。随着波数的增大,弹簧刚度对DSCF分布的影响变小。

当弹簧刚度越趋近于+∞,即边界越趋近完美边界,计算所得DSCF的峰值和分布形状越完美边界时的峰值和分布形状。这也说明了计算的正确性。图2(d)可以观察到DSCF在夹塞周围出现了多处峰值,也说明高波数时波向各个方向散射的能量变的更多,这种共振散射现象在Rajabi和Hasheminejad文章中有记录[23]。

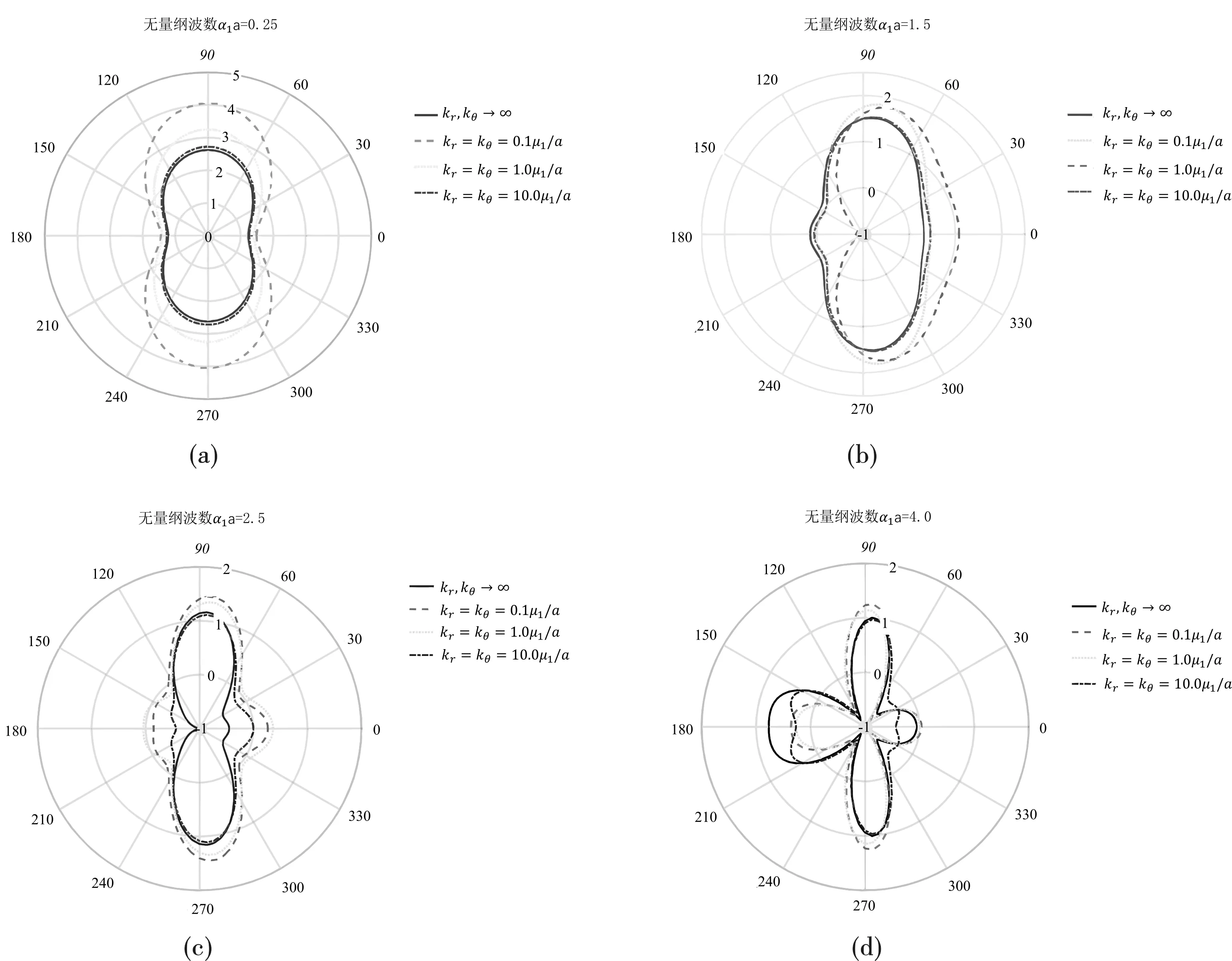
图 2 不同弹簧刚度情况下,夹塞周边DSCF分布Fig. 2 Distribution of DSCF around the inclusion with different values of spring stiffness

图3为不同弹簧刚度条件下,界面不同位置的DSCF随波数变化图像。DSCF最大值出现在界面θ=π/2位置,此时的无量纲波数为0.25,并且弹簧刚度对DSCF的影响很明显。随着波数增大,不同弹簧刚度条件下的DSCF都有下降的趋势,并最终趋于1。从图3(d)观察到在θ=π位置,无量纲波数为2.25时,出现较大的负值,表明此时有较大的切向拉应力在迎波面产生。

图 3 不同波数时圆夹塞周边DSCF分布Fig. 3 Distribution of DSCF around the circular inclusion with different wave numbers

最后,分析弹簧刚度和波数共同作用时夹塞周边DSCF最大值的变化,如图4。随波数增大DSCF最大值有减小的趋势。当弹簧刚度比较大时,DSCF最大值随波数呈现波浪式起伏,而在连接键刚度变弱后,这种起伏随之变弱。

图 4 不同弹簧刚度组合下最大DSCF值Fig. 4 Maximum DSCF value under different spring stiffness combinations

5 瞬态响应分析

爆破或者地震引起的地震波具有明确起始时间也不是周期性的,与稳态波相比有一定的差别。在分析了稳态波入射作用下的散射和动应力集中问题后,进一步求出瞬态波入射作用下的散射和动应力集中。

获得瞬态波反应的通常做法是先求得稳态波入射的反应然后将不同频率入射波的反应叠加。Fourier变换在整个过程中起重要桥梁作用。分析一个线性系统在输入任意一个函数f(t)时的瞬态反应g(xi,t)由式(17)确定

(17)

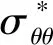
(18)

剧烈的地震扰动会产生一个移动的小波,它的形状由地球上弹性波的吸收光谱的性质决定[24]。Ricker在文章中将尖锐的波形转换成由地球吸收光谱截止的陡度决定的移动的“小波”(雷克子波),给出了雷克子波的数学证明及数学表达式。因此本文选择雷克子波作为入射的瞬态波形可以很好的模拟爆破产生的扰动。

雷克子波收敛快,旁瓣的幅度比上主瓣幅度的值为,约等于2.241。雷克子波在时域上的表达式为[24]

(19)

假设瞬态波在t=0时刻主瓣峰值传到即圆夹塞中心,此时t0=0,T为雷克子波一个波长对应时间。雷克子波的傅里叶变换表达式如式[25]

(20)

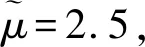
当雷克子波峰值频率为1000时DSCF随时间变化曲线如图5所示,测点位于π/2处。DSCF曲线形状与波形形状相似,两处DSCF中凹陷处的最小值与凸出部分的最大值之比为2.07,接近雷克子波主瓣与副瓣的波形幅值之比2.241。瞬态DSCF最大值分别为6.71、5.56、4.74、4.57,分别对应kr=kθ=0.1μ1/a、1.0μ1/a、10.0μ1/a。

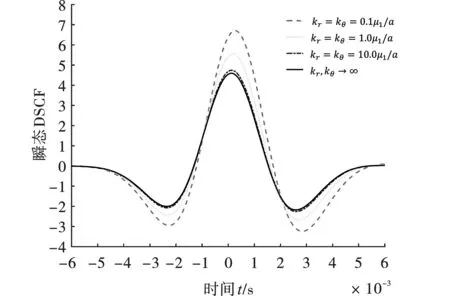
图 5 不同弹簧刚度时雷克子波造成的环向方向DSCF Fig. 5 The circumferential DSCF generated by the Rick wavelet with different values of spring stiffness

不同峰值频率wp条件下,弹簧刚度对DSCF的影响如图6所示。峰值频率wp=300,kr=kθ=0.1μ1/a时DSCF最大值为6.93,当wp增加到6000弹簧刚度不变时,DSCF最大值减小到2.83。

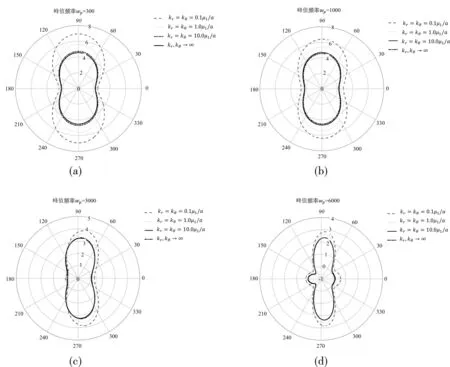
图 6 不同峰值频率wp条件下弹簧刚度对DSCF的影响Fig. 6 The influence of spring stiffness on DSCF under different peak frequencies wp

瞬态波入射时,与稳态波的最大区别在于其在时域上有限,因此反射波和入射波有可能不会同时作用在圆孔周边。但是,当频率较小时,波形的前部被反射并与其他部分一起对夹塞产生影响。所以在相同的弹簧刚度条件下,当瞬态波的峰值频率wp设为300时,DSCF最大值达到了6.93,而当峰值频频增加到6000时,DSCF最大值下降到2.83。

弹簧刚度对圆形夹塞的动应力响应也与峰值频率有关。峰值频率较小时,弹簧刚度对环向动应力影响较大。随着峰值频率上升,弹簧刚度对动应力的影响在减弱。