多边矩阵的块拉长Te运算
2022-09-19马萱航夏琪祺郏君乐张应山
罗 纯,马萱航,夏琪祺,郏君乐,潘 翔,张应山
(1. 上海应用技术大学 理学院, 上海201418;2. 硅湖职业技术学院 校长室, 江苏 昆山215332;3. 华东师范大学 金融与统计学院, 上海200241)
象数学逻辑[1]主要研究对象为多个复杂系统并探究其内部存在的某种运算关系,复杂系统包含2部分,根据变量为输出变量或输入变量对空间给出定义,输出变量构成的空间定义为象空间,输入变量构成的空间定义为卦空间。在对象空间内数据存在的客观规律研究的过程中,结论是可逆数据的变换分析结论是具有再现性的。在一般的矩阵中,矩阵按行拉长vecr运算和按列拉长vecc运算也被定义为常用的运算法则。推广到多边矩阵理论中,这2个运算也形成多边矩阵理论的基本运算之一,定义为块拉长Tensor运算,分别用Te、te表示。
文献[2-3]中主要探究了不同指标问题的运算规律和相关性质,并给出其从特殊情况推广至一般场合的证明;文献[4-5]中分别利用多边矩阵的基阵和置换矩阵探究了在多边矩阵中存在的一些一般运算法则,文献[6-9]中的按行拉长Vr=vecr和按列拉长Vc=vecc及 其相应的逆的运算方法,也可以归纳为是多边矩阵块拉长Te及其逆Te-1运算规则的一种特殊情况,即总体拉长te及其逆te-1运算的情况。而本文则是为了将一般矩阵按行拉长vecr的运算法则和性质推广至多边矩阵,并探究多边矩阵块拉长Tensor运算规则。
1 多边矩阵块拉长Tensor 运算的定义和基本定理
定义1.1设多边矩阵的一个剖面可以表示为
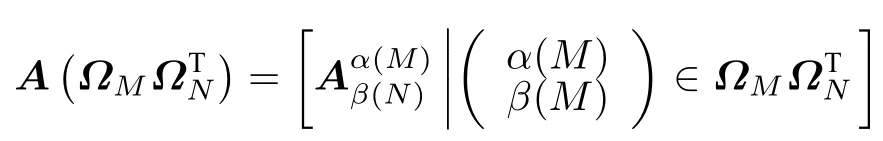

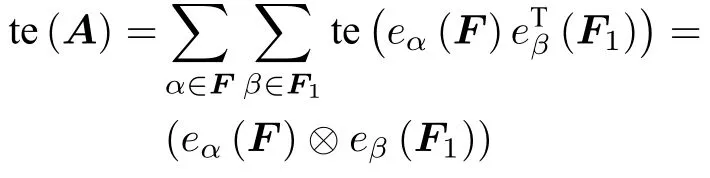
称te(A)是多边矩阵A的总体拉长,其中为基阵总体拉长te的 基本拉长定义。其他拉长同理可得。

令eα(F)、eβ(F1)、eλ(K)、eµ(K1)分别为F、F1、K、K1型多边矩阵的标准基阵。
记IF、IF1、IK、IK1分别为F FT、、KKT、型单位多边矩阵。又记分别为F(F×K)T、型多边矩阵。又记HKT多边矩阵为

则
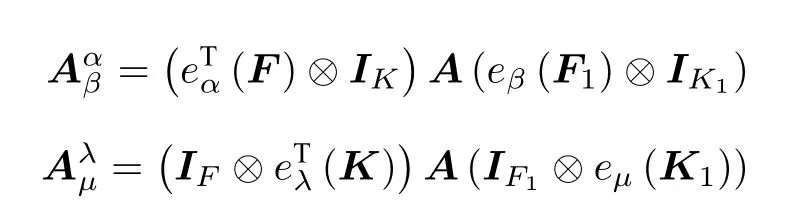
定理1.1如果设矩阵A的一个剖面表示为,那么如下结论是等价的。
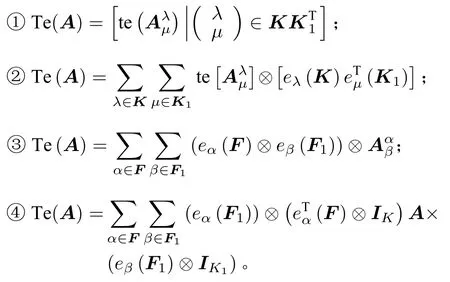
证由定义1.1可知等式①和②是等价的。等式③和④表达了同一个等式,因此它们是等价的。
只需证明等式②和等式③是等价的即可。
根据多边矩阵A的定义可知,多边矩阵A沿框架的基阵为
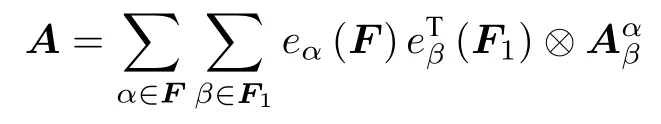
而多边矩阵A沿框架的基阵表示是
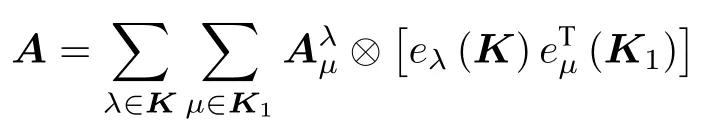

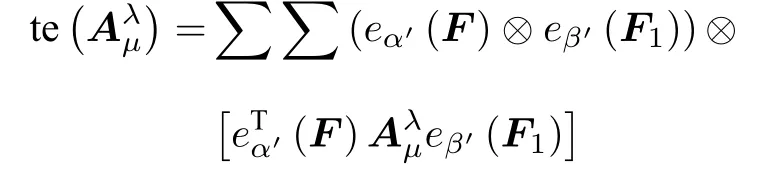
可知

这说明等式③和等式②是等价的。即证。
推论1.1若A为型多边矩阵,则A沿框架的块拉长为
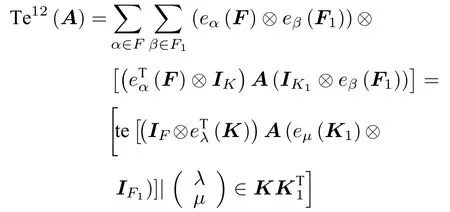
若A为型多边矩阵,那么沿A框架的 块拉长为

若A为型多边矩阵,那么A沿框架的块拉长为

2 多边矩阵块拉长Te 的基本性质
性质2.1(线性与转置)如果A,B为×型多边矩阵,a、b为数值,*T定义为多边矩阵转置,则
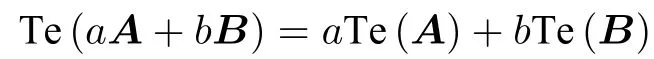
设多边矩阵A沿剖面的基阵表达性质为
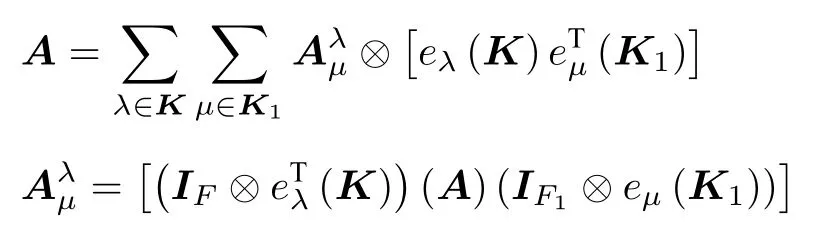
记块转置T (A)为:

则
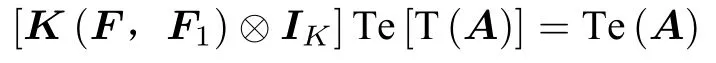
其中

为换位多边矩阵。
证明用定理1.1的结论4可知
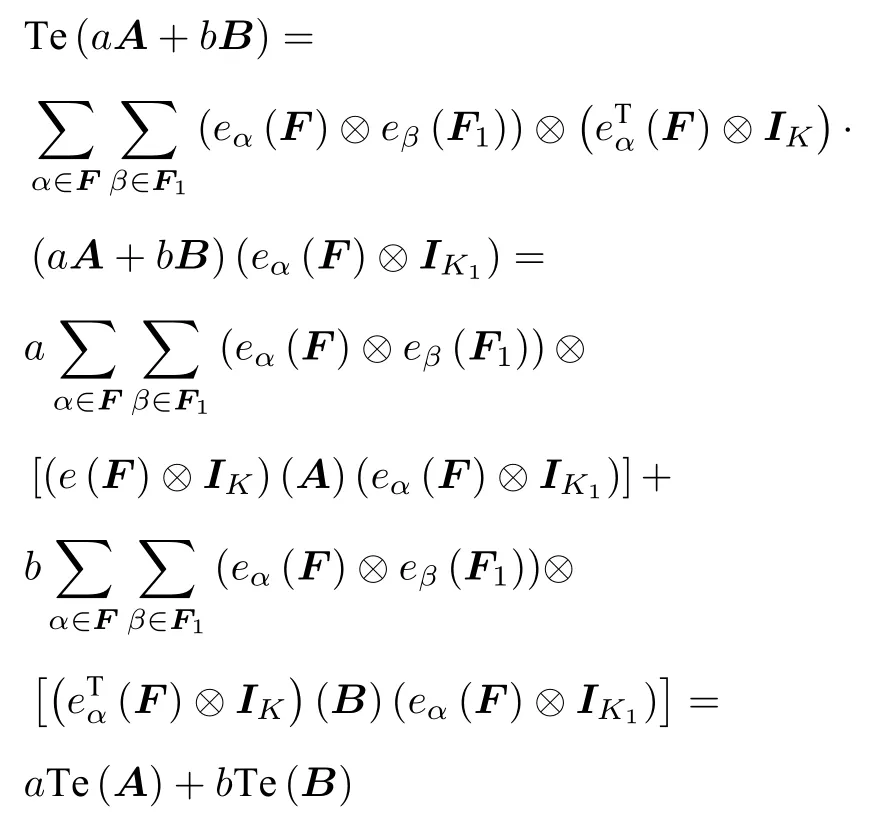
因为

所以

即证。
性质2.2(Kronecker积性质)如果A、B分别为型多边矩阵,则
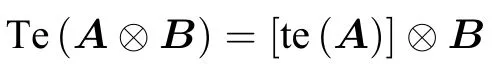
证根据定理1.1已知,,,可以得到
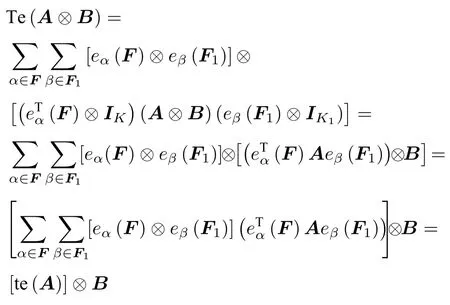
即证。
性质2.3(乘积性质)如果A为型多边矩阵,C为K0KT型多边矩阵,D为型多边矩阵,则
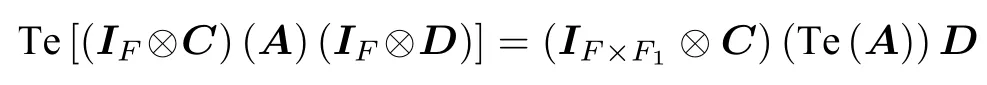
证根据定理1.1已知,
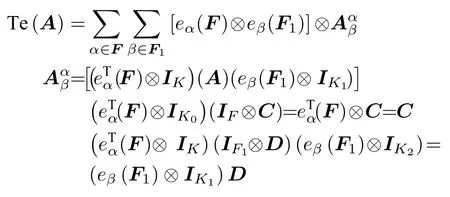
可以得到:

即证。
性质2.4(乘法拉长)如果A为型多边矩阵,C为F0FT型多边矩阵,D为型多边矩阵,则

证根据性质2.1已知,

根据定理1.1已知,

可以得到:
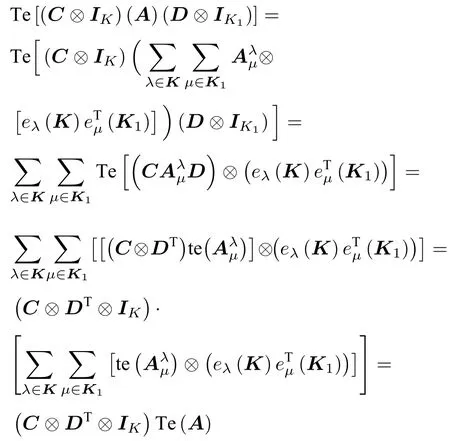
即证。
3 块拉长Teij 之间的关系
定义3.1如果A为型多边矩阵,多边矩阵A沿剖面的基阵表达性质为

那么定义运算记号te⊗IK为

Te=Te11=te⊗IK
则。
如果A为型多边矩阵,多边矩阵A沿剖面的基阵表达性质为

那么定义记号IK⊗te为

如果A为型多边矩阵,多边矩阵A沿剖面的基阵表达性质为
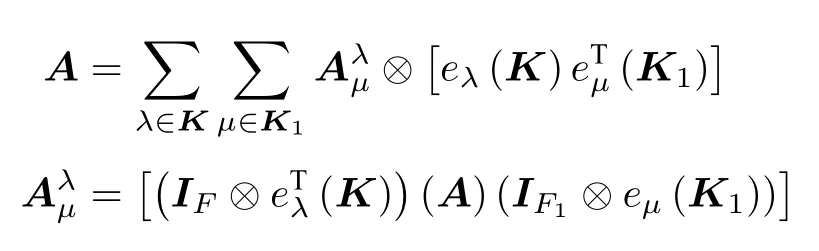
那么定义记号te⊗te 为
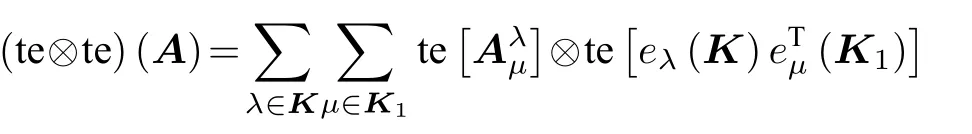
则te=te⊗te, 定义为总体拉长。
性质3.1(块拉长的嵌套性质)如果A为型多边矩阵,Te(A)=Te11(A)为多边矩阵A沿框架的 块拉长,te(A)为A沿框架的总体拉长,(IF⊗te)(T(A))为Te(A)=Te11(A)沿框架的块拉长,则

其中, Te11=Te 。
证根据定理1.1和多边矩阵的基阵表达性质可知,
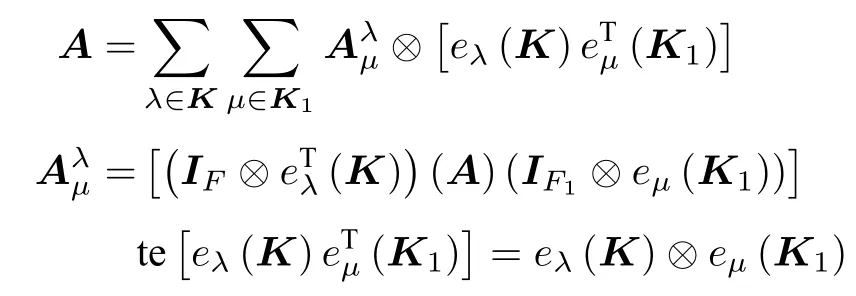
根据总体拉长的定义可知,
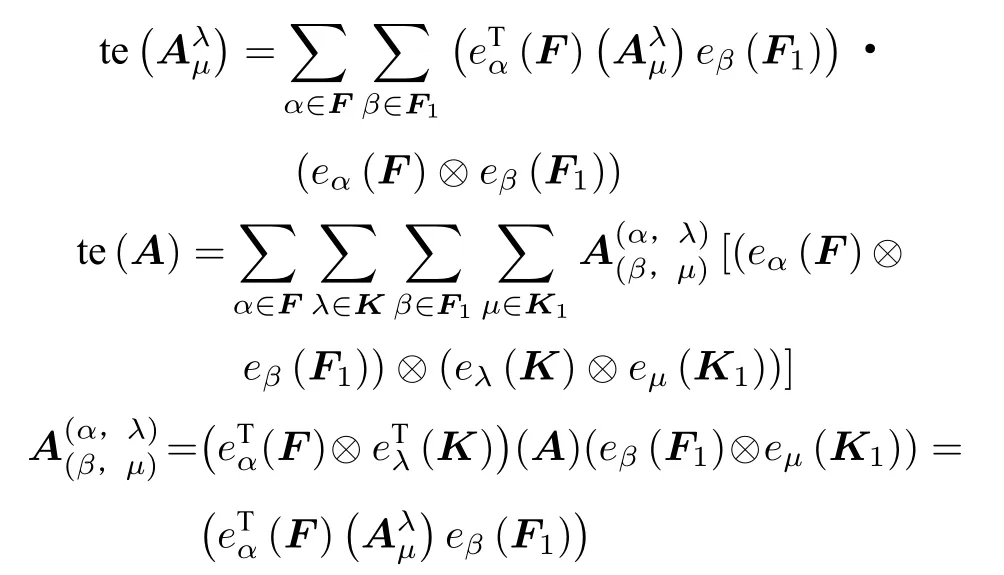
可以得到:

因为te⊗te与的乘法位置无关,所以

即证。
性质3.2(多边矩阵块拉长Te和块拉长Teij的关系)
(1) 如果A为型多边矩阵,那么AK(F1,K1)T为型多边矩阵,K(K,F)A为型多边矩阵,则

(2) 如果A为型多边矩阵,那么K(F,K)A为型多边矩阵,AK(K1,F1)T为型多边矩阵,则

(3) 如果A为型多边矩阵,那么K(F,K)AK(F1,K1)T为型多边矩阵,则
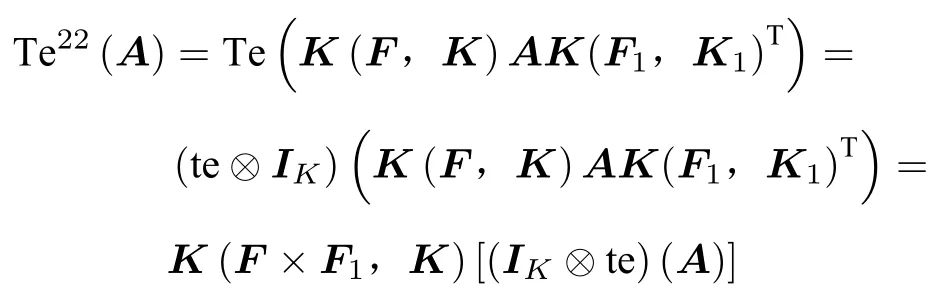
其为型多边矩阵。
(4) 如果A为型多边矩阵,那么(A)T是型多边矩阵,则,

证(1)先证结论3根据推论1.1,如果A为型多边矩阵,那么多边矩阵A沿剖面的基阵表达性质为

于是,采用记号(IK×te)满足

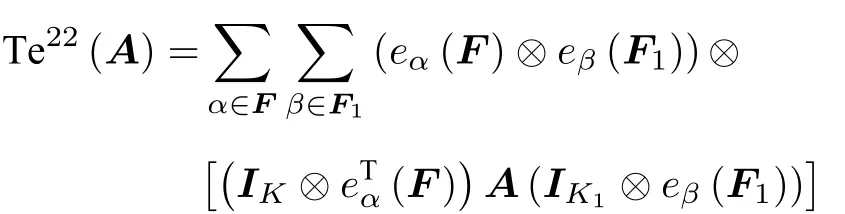

于是得到命题的结论3的最后等式。其他等式是定义。
证(2)根据上述结论3可知
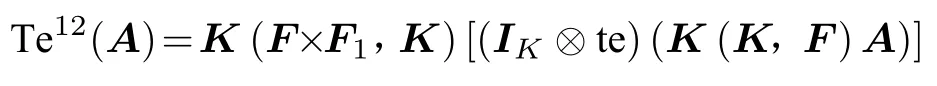
于是得到命题的结论1的最后等式。其他等式是定义。
证(3)根据上述结论3可知
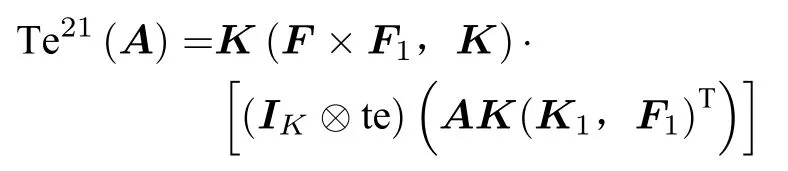
于是得到命题的结论2的最后等式。其他等式是定义。
证(4) 如果A为型多边矩阵,则(A)T是K1FT×F1KT型多边矩阵,用结论1和2知,
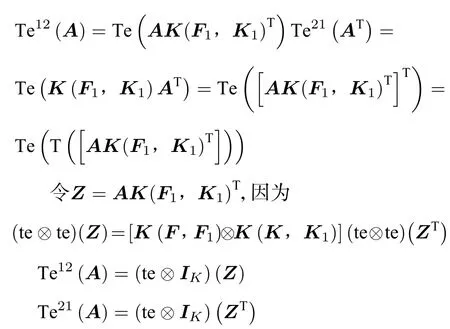
所以

即证。
4 结 语
本文的推导过程严格证明了多边矩阵的块拉长Te和块迹Tr存在着密切关系;也与总体拉长te和总体迹tr关系密切,即Te=te⊗IK和Tr=tr⊗IK。而总体拉长te与运算te⊗te运算有关,总体迹tr与运算tr⊗tr运算有关。块拉长Teij基本是等价的拉长运算,与记号IK⊗te具有关系。各种运算之间仅仅相差置换多边矩阵,说明各种块拉长Tensor运算都是可逆的等价运算,具有同构运算性质,是考虑再现性问题的重要运算工具。
