基于PSO优化的一类碰撞振动系统混沌控制

代晨曦，周方伟，卫晓娟

（上海应用技术大学 轨道交通学院，上海 201418）

含间隙碰撞振动系统普遍存在于机械设备中（如含齿侧间隙和轴承支承间隙的单级齿轮传动系统，由于间隙存在而导致碰撞冲击振动的发生）。由于碰撞振动系统具有强非线性，导致其具有丰富而又复杂的动力学行为（分岔和混沌等），为了避免这些有损机械结构的行为，近年来，研究者们对碰撞振动系统混沌运动控制问题进行了相应的探索和研究[1-3]。王子俊[4]针对一类单自由度碰撞振动系统的混沌运动，采用OGY方法进行控制；杜伟霞等[5]针对于两自由度弹碰系统的混沌运动控制问题，采用间歇控制方法对该系统施加控制。Lee等[6]提出了基于反馈控制思想的一类单自由度碰撞振子位置控制策略；张曹辉[7]提出基于粒子群优化算法（particle swarm optimization，PSO）算法优化支持向量机（support vector machines，SVM）的混沌运动控制方法，分别对含间隙单自由度刚性碰撞振动系统和弹性碰撞振动系统的混沌运动进行控制；林何等[8]针对多间隙齿轮-轴承系统长周期不稳定周期轨道不动点维数变异控制失稳问题，以轴承预载荷为摄动激励实施微扰控制，实现了混沌吸引子向多种不同周期路径上的迁移控制。Shen等[9]研究了单自由度谐振冲击振子中的擦边诱导混沌的控制问题，采用实时离散时间反馈控制策略，将其控制为周期运动。Wei等[10]针对一类含间隙碰撞振动系统的混沌运动控制问题，提出了一种基于AHGSA的无模型混沌控制方法。

虽然研究者们关于碰撞振动系统混沌运动控制研究取得了一定的成果，但相较该类系统的动力学研究而言，控制器设计不依赖于被控系统精确数学模型的碰撞振动系统混沌运动控制研究，还有待进一步探索和深入[11]。而且，将PSO算法引入碰撞振动系统混沌运动控制的相应研究仍然鲜见。

基于此，考虑到神经网络控制具有不依赖于被控系统精确数学模型的优势，本文针对一类含间隙单自由度刚性碰撞振动系统的混沌运动控制问题，提出一种基于PSO优化径向基函数（radial basis function，RBF）神经网络的参数反馈混沌运动控制方法：分析系统运动随激励频率变化所产生的分岔与混沌，总结系统分岔及混沌运动的参数分析判据，据此设计了RBF神经网络参数反馈混沌控制器，并采用PSO算法优化控制器的参数(即隐层节点中心、中心宽度、权值)，通过给系统可控参数施加小扰动，达到将混沌运动控制为稳定周期运动的目的。通过仿真实验验证了该控制方法的可行性及有效性。该方法无需被控系统精确数学模型及不动点的位置等先验知识，可用于模型未知或难以建立精确数学模型情况下的混沌运动控制。

1 系统力学模型及混沌运动

本文研究的是如图1所示的单自由度含间隙碰撞振动系统的混沌运动控制问题。如图1所示，质量块M与水平支撑面间无摩擦（水平支撑面为光滑平面），质量块M在简谐激振力Psin(ΩT＋τ)作用下开始振动，运动的位移用X表示，当质量块M位于平衡位置时，其与右侧刚性约束的间隙为H。

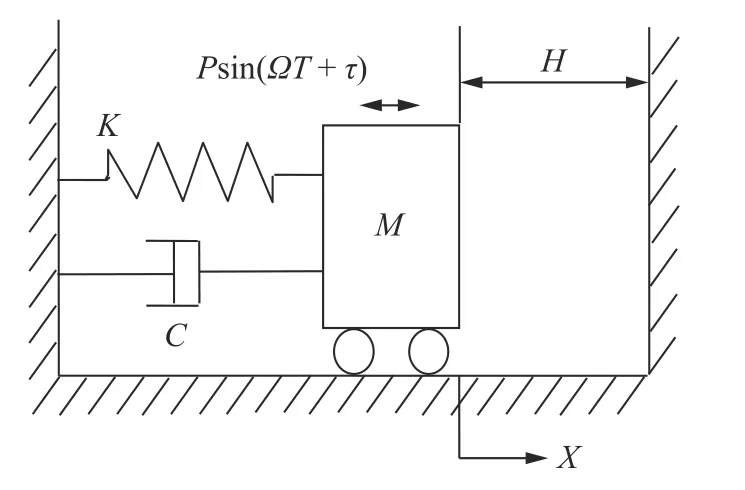
图1 单自由度含间隙碰撞振动系统的力学模型Fig. 1 The mechanical model of a single-degree-of-freedom vibro-impact system with clearance

图1中，M为质量块的质量，C为阻尼系数（线性阻尼器）,K为刚度（线性弹簧）。

当质量块M运动的位移为H时，与右侧刚性约束发生碰撞，这时质量块的速度方向发生改变，以新的初始条件做往复运动。若碰撞持续时间忽略不计，则图1所示系统运动微分方程为

为揭示一定参数条件下，图1中系统的混沌运动产生机理，选择碰撞后瞬时的σ截面，即

其中，θ=ωtmod 2nπ）为Poincaré截面。在ζ=0.2，R=0.8，h=0.05的参数条件下，分析混沌运动与系统参数（即简谐激振力频率ω）之间的关联关系及表现特征，结果如图2～图4所示。

图2 系统随ω变化的分岔图Fig. 2 The bifurcation diagram of system with ω changing

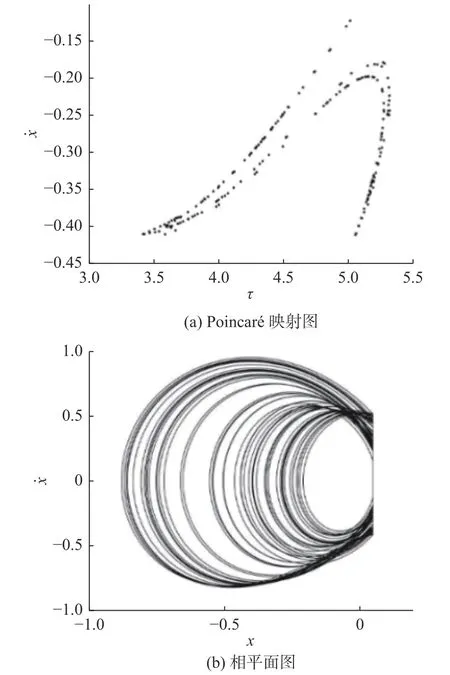
图4 混沌吸引子（ω=2.65）Fig. 4 Chaotic attractor (ω=2.65)

由图2可知，当简谐激振力频率ω在一定范围内变化时，图1所示系统运动经倍周期分岔演化为混沌运动。当ω∈[2.50,2.56]时，该系统具有稳定的周期1-1运动（用符号n-p区分系统运动的类型；符号n-p中n代表激励周期数，p代表碰撞次数）；在ω∈[2.56,2.62]时，系统由周期1-1运动经过第一次倍化分岔，演变为周期2-2运动；当ω∈[2.62,2.63]时，系统由周期2-2运动经过第二次倍化分岔，演变为周期4-4运动；随着ω继续增大，系统会继续发生倍化分岔直至通向混沌状态。当ω∈[2.67,2.69]时，混沌运动中还具有周期窗口。

图3为图2中的系统分岔图所对应的Lyapunov指数谱图。Lyapunov指数作为一个定量指标[12]，在图3中也直观地表明了系统运动性态变化与简谐激振力频率ω之间的关系。图3中，最大Lyapunov指数用λ1来表示，当λ1＜0时，系统运动为稳定的周期n-p运动；当λ1＞0 时，系统运动为混沌运动；当λ1=0、而λ2＜0时，系统发生倍周期分岔。

图3 系统Lyapunov指数谱图Fig. 3 The Lyapunov spectra of system

ω=2.65，ζ=0.2，R=0.8，h=0.05时的混沌吸引子和相平面图如图4所示。由图4（a）可见，在Poincaré截面上为成片的散落点集，且有层次结构；由图4（b）也可以看到，此时系统相平面图不重复且杂乱无章。图4（a）和图4（b）均表明系统运动为混沌运动。

2 基于RBFNN的混沌控制器设计

基于参数反馈混沌控制法的原理来控制混沌运动。即：利用RBFNN控制器输出一个微小且有界的扰动量Δω施加于系统的可控参数--简谐激振力频率ω，通过对其动态微幅调整，从而将混沌运动控制到稳定的周期运动。

图5为本文设计的混沌控制器结构。控制器输入层的2个输入为能够反映系统趋近于稳定周期运动趋势的相邻两次迭代后Poincaré截面上的投影点间的距离（即d(k)=‖X(k)-X(k-1)‖、d(k-1)=‖X(k-1)-X(k-2)‖；X(k)为第k次迭代后被控系统状态变量X=[x˙,τ]的值）。控制器的输出层为一个节点；控制器输出量则为激励频率的微幅调整量，为保持控制的有效性，设定最大调整量为umax，则-umax＜u＜umax。输入层到隐含层的激活函数选用高斯径向基函数。在团队前期研究成果的基础上，经反复试验对比，本文确定隐层节点数为5。

图5 控制器结构Fig. 5 The structure of the controller

3 基于PSO的控制器参数优化

3.1 适应度函数的构建

适应度函数用来定量评价基于RBF神经网络所设计的混沌控制器对被控系统的控制能力以及引导PSO算法优选控制器参数。控制目标是使得所设计的控制器将图1所示单自由度含间隙碰撞振动系统的混沌运动控制为稳定的周期运动。本文选定相邻两次迭代后Poincaré截面上投影点间的距离作为判断依据，构建控制器参数优化选择时所应满足的适应度函数如下：

式中：X(k)为受控系统状态变量X的值；u(k)为控制输入；d*为Poincaré截面上相邻2点距离的期望值；η为(0,1)区间上均匀分布的随机数。

采用PSO算法优化混沌控制器参数时，每个粒子的搜索结果都要用于去计算适应度函数的值，并进行比较，使适应度函数取得最小值的搜索结果，即为控制器的最优参数。

3.2 基于PSO的控制器参数优化

根据图5所示控制器结构可确定PSO算法搜索得到的最优解空间的维数为20。在t时刻第i个粒子在解空间中的位置Pi(t)={Pi,1(t),Pi,2(t),···,Pi,20(t)}，速度Vi（t）={Vi,1(t),Vi,2(t),L,Vi,20(t)}，i=1,2,···,M；粒子通过搜索得到的个体最优位置Pibest(t)={Pibest,1(t),Pibest,2(t),···,Pibest,20(t)}，群体最优位置Gbest(t)={Gbest,1(t),Gbest,2(t),···,Gbest,20(t)}。

PSO算法的速度和位置的迭代公式为

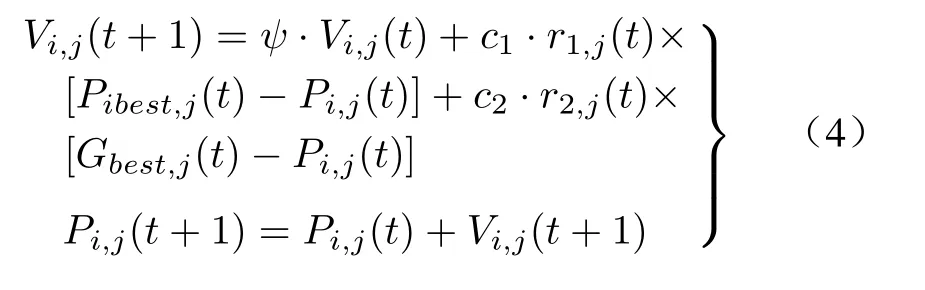
式中：ψ为惯性权值；c1、c2为加速常数；r1、r2为[0,1]区间上均匀分布的随机数。PSO算法的全局搜索能力随ψ的增大而增强；反之，PSO算法的局部搜索能力随ψ的减小而增强。为了平衡PSO算法的全局寻优能力和局部寻优能力，ψ取值从0.9线性递减至0.5。

图6所示为采用PSO算法优化混沌控制器的流程图。

图6 PSO算法优化控制器参数流程Fig. 6 The flow chart of controller parameter optimization based on PSO algorithm

4 混沌控制仿真

采用PSO-RBFNN的混沌控制方法对图4（a）所示的混沌吸引子进行控制仿真。PSO算法的参数设置为：粒子总的个数为30，粒子搜索次数为100次。为了更清楚地表示混沌运动控制效果，系统迭代500次时对混沌运动施加控制。

如图7所示，通过轨道图及相平面图展示了将混沌运动控制为周期1-1运动的控制效果。采用PSO算法优化后的控制器参数如表1所示。图7(a)、7(b)为混沌运动演化为周期1-1运动的时间历程；由图7(a)、7(b)可知，混沌运动能够很快地（在k=522时）被稳定到周期1-1轨道；图7(c)为系统稳定后的相平面图，图中一条封闭的曲线说明此时系统运动为稳定的周期1-1运动。

图7 受控周期1-1运动Fig. 7 Controlled period 1-1 motion of the system

表1 周期1-1的控制器参数Tab. 1 Parameters of controller (period 1-1 motion)

图8展示了将混沌运动控制为周期2-2运动的控制效果。采用PSO算法优化后的控制器参数如表2所示。图8(a)、8(b)为混沌运动演化为周期2-2运动的时间历程；由图8(a)、8(b)可知，混沌运动能够很快地（在k=515时）被稳定到周期2-2轨道；图8(c)为系统稳定后的相平面图，图中2条封闭的曲线说明此时系统运动为稳定的周期2-2运动。

图8 受控周期2-2运动Fig. 8 Controlled period 2-2 motion of the system

表2 周期2-2的控制器参数Tab. 2 Parameters of controller (period 2-2 motion)

从上述仿真结果可见，本文方法能够很好地实现对图1所示单自由度含间隙刚性碰撞振动系统混沌运动的有效控制，最终的控制目标不仅仅可以是周期1-1及周期2-2运动，也可以是其他周期轨道。但出于篇幅的考虑，其余周期轨道不再赘述。

5 结 语

本文研究了一类单自由度含间隙刚性碰撞系

统的混沌运动控制问题，提出了一种基于PSO优化控制器（控制器结构基于RBFNN设计）参数的混沌控制方法。首先分别采用分岔图和指数谱图描述了单自由度含间隙刚性碰撞振动系统运动在简谐激励频率变化时的变化规律及表现特征；然后采用PSO算法与RBFNN相结合而形成的智能优化控制方法进行混沌运动控制：控制器基于RBFNN的三层网络结构设计，基于Poincaré截面上相邻两点间距离最小原则建立适应度函数，以引导PSO算法对控制器参数进行优化，同时适应度函数值也可用来评价控制器对被控系统的控制能力。仿真结果表明该方法具有良好的控制效果。