分布式基阵联合定位算法仿真分析

王志刚, 陈韶华, 王 维



分布式基阵联合定位算法仿真分析

王志刚, 陈韶华, 王 维

(中国船舶重工集团公司 第710研究所, 湖北 宜昌, 443003)

在诸多水中目标定位的方法中, 相对于纯方位目标定位与跟踪算法计算量大、实时性差、定位和估计精度不高的不足, 多基阵联合定位系统具有较强的抗干扰能力和生存能力。基于此, 文中提出了一种适用于水声网络的分布式基阵联合定位方法, 分别给出了Jacobi迭代法、三角重心法和最小二乘法等算法的仿真计算模型, 比较分析了3种不同定位方法在不同基阵数和分布态势下的定位仿真性能。仿真结果表明, 基于三基阵的Jacobi迭代法定位精度和收敛性要优于其他2种算法。最后, 根据应用情况提出了适合分布式基阵联合定位的阵型、基阵数以及阵间距等参数, 以期提高对目标的定位性能和网络生存能力, 为多基阵目标定位的工程应用提供参考。

水中目标定位; 分布式基阵; 水声网络; 纯方位目标定位; Jacobi迭代法; 多基阵联合定位

0 引言

由于单基阵的探测范围小、定位精度不高,测距误差较大, 因而难于满足定位要求[1]。在实际应用中常常采用多阵联合的形式扩大探测范围和提高定位精度[2]。

纯方位目标定位与跟踪是无源定位跟踪技术的一个重要分支, 单基阵测量的目标参数中以目标方位比较容易获得，因此常常利用所测得的目标方位角信息来估计目标的位置、速度及加速度等。文献[3]详细介绍了多基阵纯方位目标定向、定位的原理和方法。文献[4]论述了定位算法评价方法和目标可观察性分析。文献[5]~[7]介绍了多基阵分布式探测定位时, 各个基阵分别探测估计目标方位, 经姿态补偿修正到统一坐标系与时间同步后, 采用多基阵联合定位算法利用每个子阵对方向角估计的结果, 通过几何算法来精确目标位置。

分布式基阵联合定位常用于水声网络对目标的探测、定位与跟踪研究中, 同时应满足高定位精度和较强的网络生存能力。对此, 文中比较分析了Jacobi迭代法、三角重心法和最小二乘法(least squares method, LSM) 3种定位方法的性能特点。并根据应用情况提出了适合分布式基阵联合定位的阵型、基阵数以及阵间距等参数, 可为分布式基阵目标定位的工程应用提供参考。

1 水面目标定位原理

1.1 Jacobi迭代法目标位置估计

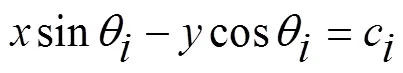
则由以上定位线方程可得

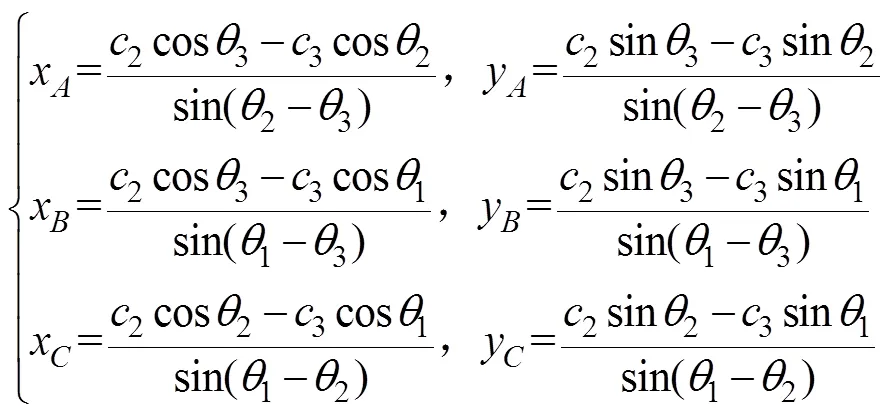
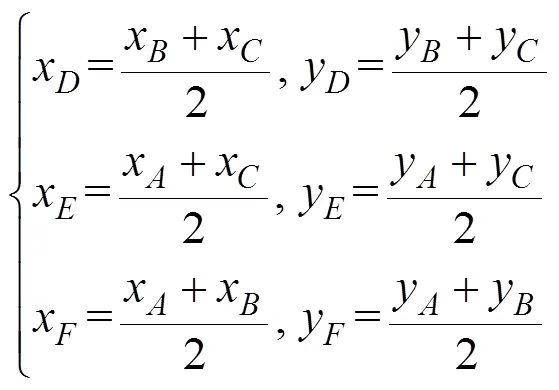
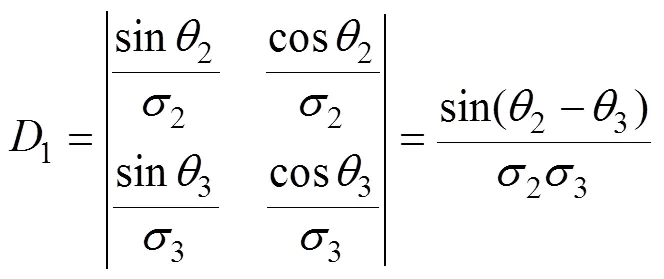
迭代法具有收敛速度快的特性, 在满足一定定位精度的条件下, 可以节省计算时间。但是迭代法是否收敛及其收敛速度与初始值的选择有关。解决好初始值的问题是保证迭代法良好性能的前提条件。

1.2 重心法目标位置估计

重心法定位的优点在于方法简单、计算量小,对硬件的要求较低, 但其定位精度依赖于单基阵测向精度, 定位精度较低。

1.3 LSM目标位置估计

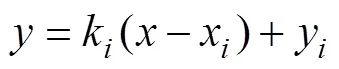
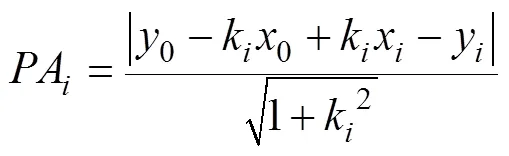
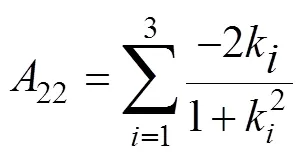
解得目标位置估计

LSM具有很好的估计特性, 但受测量误差的影响较大, 使用LSM进行定位解算会产生一定的误差, 对定位精度有一定的影响。此方法对非线性方程线性化计算需要的条件比较严格, 但是如果能够合理地布置基阵的位置和选择基阵的数量, 精确地测得方位角, LSM就能够快速准确地计算出目标位置[9]。

2 仿真结果与分析

假设目标为一水面舰船, 利用不同基阵数目、算法和阵型对目标进行定位。根据三角阵大小变化分别进行仿真。

2.1 不同基阵数目对同一目标的定位

对于多基阵纯方位目标跟踪情形, 在跟踪算法确定的前提下, 目标的跟踪或定位精度不仅与所选择的基阵数目有关, 还与目标和基阵间的相对位置有关, 因此如何动态选择基阵具有非常重要的实际意义[10]。

假设目标位置为(2 000, 2 000), 基阵1位置为(1 000, 0), 基阵2位置为(0, 1 000), 基阵3位置为(0, 0), 基阵态势图如图4所示。单基阵定向误差设均值为0, 方差为3。利用基阵1和2对目标进行双基阵定位, 基阵1、基阵2和基阵3对目标进行三基阵定位, 分别对同一目标进行多次采样测量, 其仿真结果如图5所示。图中显示了不同的基阵数对同一目标定位时的误差。

由图5可以明显看出, 对于同一目标而言, 3个基阵定位误差(1,2和3)要比2个基阵(1与2)定位的误差小得多。根据数据融合理论, 定位基阵数越多对目标的定位越精确[7], 4个基阵对目标的定位精度要比3个基阵高。但是, 4个以上的基阵对目标的定位算法更为复杂、运算量更大,对目标跟踪定位精度的提高意义不大。此外, 当网络内对单一目标定位的基阵数增加时, 网络维护的成本(时间)增加, 同时对单基阵对目标的解算时间、基阵间数据传输时间以及数据处理时间来说, 基阵越多时效性越差。所以, 对于网络基阵并不意味着对目标的定位基阵数越多越好, 3个基阵就能够实现对目标实时地跟踪和定位。

三基阵按照不同的分布态势对目标进行定位,其分布态势如图4和图6所示。对目标的定位仿真结果如图7所示。图中显示了3个基阵在不同态势下对同一目标的定位误差, 可知, 态势二定位误差要比态势一定位误差小。

当1和2不动,3从(0, 0)点开始沿45°方向朝目标点移动时, 三基阵定位误差逐渐减小,如图8所示。因此, 在大规模水下网络定位时, 优先选用图6分布态势进行定位, 若目标正好处于2个基阵的连线上, 这时目标的定位精度最差[11]。

2.2 不同方法对同一目标的定位

假设目标位置为(2 000, 2 000), 基阵1初始位置为(1 000, 0), 基阵2初始位置为(0, 1 000), 基阵3初始位置为(1 000, 1 000), 为每个探测基阵随机加入不同的方向角误差, 测量点数为100, 基阵态势如图5所示。按照三基阵重心法、Jacobi迭代法和LSM分别进行计算定位误差, 结果如表1所示。

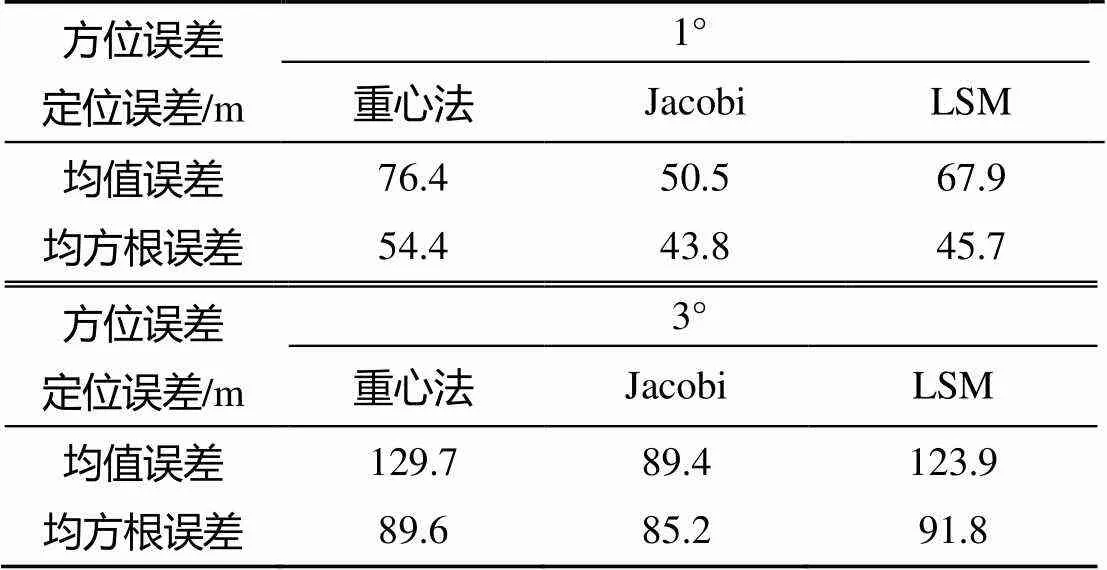
表1 不同定位方法误差比对

由仿真结果可见, 对于同一阵型同一目标而言, 方向角误差越小, 定位精度越高; 对于不同的定位方法而言, 重心法和LSM的定位误差和均方根误差均较大, Jacobi迭代法则最小。因此, 多基阵联合定位时, 使用Jacobi迭代法其定位精度和收敛性要优于其他2种算法。

在工程实现中, 与其他2种定位方法相比, Jacobi迭代法代码量较大, 运算时间较长, 对硬件资源需求较高。但是, 结合当前DSP芯片数据处理速度能力和Flash存储容量, 该方法能够实时实现。工程应用中由于Jacobi迭代法定位精度高, 是优先选择的方法。

3 结束语

文中对分布式基阵纯方位角联合定位进行了仿真, 分析了3种不同定位方法在不同基阵数量以及不同布放态势下的定位误差, 提出了一种适用于水声网络的多基阵定位方法。从以上仿真结果可以看出：

1) 相同基阵不同算法对同一目标定位时, Jacobi迭代法误差最小;

2) 基阵数量越大, 定位误差越小。三基阵对目标的定位误差小于双基阵, 按照数据融合理论, 基阵越多定位误差则越小。实际应用中考虑到定位算法复杂程度及运算量大小、各基阵的数据处理时间、基阵间的数据传输时间以及最后数据处理时间等因素会随定位基阵数量增加而增加, 为了尽可能提高定位的时效性, 实现对目标跟踪定位的实时性, 对单一目标的跟踪定位基阵数不宜超过3个;

3) 基于水声网络对目标跟踪还应有效解决网络的生存能力和参数的快速精确估计等问题。结合目前水声通信距离、单基阵对目标的探测距离、水声网络生存能力及未来水下武器自导能力等因素, 建议分布式基阵布放间距在1 000～1 500 m。各基阵间距过小, 对网络的控制范围有影响, 不利于水声网络大范围联合探测定位; 各基阵间距过大, 基阵间信息传输时延大, 网络开销也大, 对目标跟踪定位的时效性差; 信息传输可靠性低, 基阵间距离增加, 信息传输过程中受干扰和基阵隐蔽性就会降低。

下一步工作将通过湖上试验对定位算法进行进一步优化完善。

[1] 祝龙石, 庄志洪, 张清泰. 利用圆阵实现声目标的全空域被动定位[J]. 声学学报, 1999, 24(2): 204-209.Zhu Long-shi, Zhuang Zhi-hong, Zhang Qing-tai. An Omni-direction Passive Localization Technology of Acou- stic Target with Plane Circular Array[J]. Acta Acustica, 1999, 24(2): 204-209.

[2] 王昭, 李宏, 赵俊渭, 等. 空气声被动定位的误差分析[J]. 应用声学, 2000, 19(2)：39-43. Wang Zhao, Li Hong, Zhao Jun-wei, et al. Error Analysis of Acoustic Passive Localization in the Air[J]. Applied Acoustic, 2000, 19(2): 39-43.

[3] 刘艳丽. 被动声探测系统对目标定向、定位算法的研究[D] . 西安: 西北工业大学, 2006.

[4] 徐本连. 双(多)基纯方位目标定位与跟踪算法研究[D]. 南京: 南京理工大学, 2006.

[5] 张安民. 纯方位目标运动分析与鱼雷智能导引律研究[D]. 西安: 西北工业大学, 2002．

[6] 杜选民, 姚蓝. 多基阵联合的无源纯方位目标运动分析研究[J]. 声学学报, 1999, 24(6): 604-610．Du Xuan-min, Yao Lan. Passive Bearings-only Target Mo- tion Analysis Based on Association of Multiple Arrays[J]. Acta Acustica, 1999, 24(6): 604-610.

[7] 关欣, 何友, 衣晓. 双基阵纯方位水下被动目标跟踪性能仿真分析[J]. 系统仿真学报, 2003, 15(10): 1464-1466．Guan Xin, He You, Yi Xiao. Emulational Analysis on the Per- formance of Underwater Bearing-only Passive Target Track- ing Using Two Arrays[J]. Journal of System Simulation 2003, 15(10): 1464-1466．

[8] Landau B V, West W. Estimation of the Source Location and the Determination of the 50% Probability Zone for an Acoustic Source Locating System(SLS) Using Multiple Systems of 3 Sensors[J]. Applied Acoustics, 1997, 52(1): 85-100.

[9] Fan Z P, Ma J, Jiang Y P, et al. A Goal Programming Approach to Group Decision Making Based on Multiplicative Preference Relations[J]. European Journal of Operational Re- search, 2006, 174(1): 311-321.

[10] Kaplan L M．Node Selection for Target Tracking Using Bear- ing Measurements from Unattended Ground Sensors [C]// 2003 IEEE Aerospace Conference Proceedings. Piscat- away, NJ, USA: IEEE, 2003, 2137-2152.

[11] Kaplan L M．Transmission Range Control During Autonomous Node Selection for Wireless Sensor Networks[C]//2004 IEEE Aerospace Conference Proceedings. Piscataway, NJ, USA: IEEE, 2004, 2072-2087.

Simulation Analysis of Joint Localization Algorithm Based on Distributed Arrays

WANG Zhi-gang, CHEN Shao-hua, WANG Wei

(The 710 Research Institute, China Shipbuilding Industry Corporation, Yichang 443003, China)

A multi-array joint localization system has the performances of strong anti-interference and survivability, compared with the bearing-only target localization and tracking algorithm, which needs a large amount of calculation and is of poor real-time performance and low accuracy of localization and estimation. In this paper, a distributed arrays based on joint localization algorithm is proposed for underwater acoustic network. Simulation models of the localization methods of Jacobi iteration, triangular center of gravity, least square method(LSM) are presented. The simulation performances of three localization methods for different array numbers and distribution situations are analyzed and compared. Simulation results show that the Jacobi iteration method with tri-array can achieve better positioning accuracy and convergence performance than the other two methods. Furthermore, the suitable parameters of array layout, array numbers, and distances among arrays for distributed arrays joint localization are proposed to improve the target localizing performance and the network survivability. This study may provides a reference for engineering application of multi-array target positioning.

underwater target localization; distributed array; underwater acoustic network; bearing-only target localization; Jacobi iteration method; multi-array joint localization

TJ630.34; TB566; TN959.1

A

2096-3920(2018)05-0433-06

10.11993/j.issn.2096-3920.2018.05.009

2018-08-08;

2018-09-08.

国家重点研发计划(2016YFC1400200).

王志刚(1980-), 男, 高级工程师, 主要研究方向为水下系统与网络技术.

王志刚, 陈韶华, 王维. 分布式基阵联合定位算法仿真分析[J]. 水下无人系统学报, 2018, 26(5): 433-438.

(责任编辑: 杨力军)