一题多解拓展思维 触类旁通提升素养——一道模考题的探究

王 义

(安徽省砀山中学，235300)

一、试题呈现

设抛物线M:y2=2px(p>0)的焦点为F,点P(4,m)(m>0)是抛物线M上的一点,且|PF|=5.

(1)求抛物线M的方程;

(2)设经过点F的直线l交抛物线M于A,B两点(A,B异于点P),点B关于x轴的对称点为C,若∆FAC的面积为6,求直线l的方程.

二、总体分析

本题是以抛物线为载体,表面上是考查直线方程与三角形面积相关问题,实为考查圆锥曲线的对称问题及直线恒过定点问题及直线斜率之和(积)、之比为定值问题,能培养学生发现问题、解决问题的能力,提升运算能力、逻辑推理及化归与转化能力,体现了数学运算及逻辑推理等数学核心素养.

三、解法探究

对第(1)问,易知抛物线M的方程为y2=4x,具体过程略下面主要考虑第(2)问的解答.

视角1直接运用三角形面积公式

解法1由题意可知直线AB的斜率不能为0,由焦点F(1,0),可设直线AB的方程为x=my+1,点A(x1,y1),B(x2,y2),C(x2,-y2).

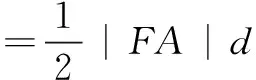
=4|m|=6，

故直线AB的方程为2x±3y-2=0.

视角2运用抛物线性质

解法3由题意可知直线AB的斜率存在,设直线AB的倾斜角为α,直线AB的方程为y=k(x-1),代入抛物线方程y2=4x,得

k2x2-(2k2+4)x+k2=0.

设点A(x1,y1),B(x2,y2),C(x2,-y2),注意k=tanα,则

所以直线AB的方程为2x±3y-2=0.

解法4由解法3,可得

故直线AB的方程为2x±3y-2=0.

视角3灵活运用面积公式

解法5由题意可知直线AB的斜率不能为0,设点A(x1,y1),B(x2,y2),C(x2,-y2),直线AB的方程为x=my+1,代入y2=4x,得y2-4my-4=0,y1+y2=4m,y1y2=-4.

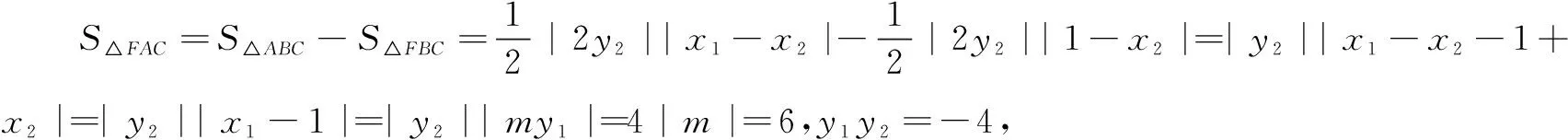
故直线AB的方程为2x±3y-2=0.

评注解法5利用几何图形求解面积,得出直线方程,注意点A,B的位置,必要时可以分类讨论,能有效培养学生直观想象的数学核心素养.

视角4利用三角形面积的坐标公式

解法6同上设点A(x1,y1),B(x2,y2),C(x2,-y2),直线AB的方程为x=my+1,可得y1+y2=4m,y1y2=-4.

故直线AB的方程为2x±3y-2=0.

评注利用三角形面积的坐标形式,方法直接、简单易懂,是最佳策略.

视角5转化思路巧解三角形面积

解法7设点A(x1,y1)，C(x2,y2),则点B(x2,-y2).设直线AC的方程为x=my+n,代入y2=4x,得y2-4my-4n=0,y1+y2=4m,y1y2=-4n.

所以直线直线AC的方程为x=my-1,恒过定点(-1,0).

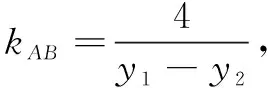
四、拓展探究

仿照上述问题求解过程,不难证明下列结论(限于篇幅,这里从略).

以上4个结论在椭圆,双曲线中也有类似的结论,读者可自行探究.

五、反思提升

从不同的角度出发去思考问题,可得到不同的解法,发现知识间的内在联系,体会知识间的转化与化归,构建知识间的网络体系.这样既能提高分析解决问题的能力,又能培养学生对数学学习的兴趣,充分调动学生学习的积极性.另外，作为一线教师,不能只停留在解法的探究上,还应该引导学生对题目深入探究,发挥题目的最大价值,让学生能做一题,通一类,真正实现一题多解,多解归一.