AGC 机组动态优化调度模型的凸松弛及其双层迭代算法
2022-09-19孙名轶
赵 霞,梁 钰,孙名轶,毛 杨
(输配电装备及系统安全与新技术国家重点实验室(重庆大学),重庆市 400044)
0 引言
自动发电控制(automatic generation control,AGC)是维持电力系统频率和联络线功率的主要手段[1]。常规AGC 根据当前频率和联络线功率偏差调节AGC 机组出力[2],难以适应高比例可再生能源接入的情况[3]。随着“碳达峰·碳中和”目标的提出,可再生能源迎来新一轮发展高潮,AGC 也将面临更大挑战[4]。
为克服常规AGC 控制滞后的问题,文献[5]提出AGC 动态优化控制,将AGC 控制问题建模为以AGC 调节成本最小为目标、AGC 性能指标为约束的AGC 机组功率优化决策问题。文献[6]进一步根据文献[5]的优化结果整定AGC 比例-积分控制器的参数。文献[7]改进了文献[5]优化模型中的频率预测方法。文献[8]将机组一次调频功率限额及调频死区纳入AGC 动态优化控制模型。
基于AGC 动态优化控制,文献[3]提出了AGC动态优化调度的思路:以日前计划为基础,基于未来10 min 或15 min 的负荷预测结果,考虑频率和联络线控制偏差、机组调节特性等时段耦合约束,以AGC 调节成本最小或控制性能最优为目标,在1 min 或更小时间尺度上决策未来各时段AGC 机组的调节功率。与文献[5]相比,文献[3]更关注所提调度模型与发电计划的衔接。此后,文献[9]将功率损耗和支路/断面功率约束纳入AGC 动态优化调度模型。文献[10]考虑网调/省调AGC 机组在调频责任和特性上的差异,提出网省两级AGC 机组的协调调度模型。文献[11]则关注风电功率随机变化的影响,提出了AGC 机组动态优化调度的机会约束模型。
从模型属性上讲,文献[5-7]的AGC 动态优化控制模型是混合整数非线性规划(mixed-integer nonlinear programming,MINLP)模型,上述文献多应用互补松弛技术将MINLP 模型转化为非线性规划(nonlinear programming,NLP)模型,采用内点法求解。文献[8]通过线性化机组最小持续爬坡时间约束,将原模型转化为混合整数线性规划(mixedinteger linear programming,MILP)模型。与AGC动态优化控制类似,文献[3,9-11]所研究的AGC 机组动态优化调度模型也是MINLP 模型(文献[9]进一步引入非线性功率损耗约束),模型求解难度大。因此,现有AGC 机组动态优化调度模型均采用进化规划算法求解。该类算法属于随机优化算法,可方便处理复杂约束,但计算量大[12],难以满足大规模系统AGC 机组动态优化调度的要求。此外,随机优化算法解的稳定性较差,相同计算环境下2 次运行所得优化结果可能不同,不利于AGC 机组的调度决策。针对以上问题,本文基于凸优化理论提出了AGC 机组动态优化调度模型的改进算法。
1 AGC 机组动态优化调度模型
1.1 决策变量与目标函数
本文沿用AGC 机组动态优化调度研究的时间尺度[9-11],采用15 min 为调度周期。以互联电网中某个区域电网为对象,通过优化决策AGC 机组每1 min 的调节功率来最小化区域电网的AGC 调节成本。
决策变量为t时段第i台AGC 机组的爬坡功率RG,i,t及增减功率指示变量ua,G,i,t、ud,G,i,t,i=1,2,…,NAGC,NAGC为AGC 机组总数;t=1,2,…,T,T为调度周期内时段总数;ua,G,i,t和ud,G,i,t均为0-1 变量,分别用以刻画t时段第i台AGC 机组的出力相对前一时段出力的增减状态,ua,G,i,t和ud,G,i,t为1 分别表示机组较前一时段增加出力和减少出力的状态,否则为0,表示出力不变化。
优化目标为整个调度周期内AGC 机组调节成本(CAGC)最低:

式中:ci为第i台AGC 机组的调节成本系数;PG,i,t和PGs,i,t分别为t时段第i台发电机组的实际出力和计划出力(不包括非AGC 机组)。
1.2 约束条件
1.2.1 区域电网运行约束
区域电网运行约束包含功率平衡约束(式(2))、支路功率约束(式(3))及断面功率约束(式(4)),如下所示:

对于功率平衡约束,需要说明以下几点:
1)机组实际出力PG,i,t与机组类型有关。对于AGC 机组:

3)本文基于功率损耗因子[15]及功率损耗迭代算法[16]计算Ploss,t(详见下文2.2 节及3.2 节)。
需要特别指出,与常规调度问题不同,AGC 调度模型的功率平衡约束中仅PD,t为预测值,其余功率分量均与系统频率偏差Δft相关。
1.2.2 机组调节特性约束
机组调节特性约束包含机组(含非AGC 机组)出力上限和下限约束(式(7))、AGC 机组爬坡功率上限和下限约束(式(8)),以及持续爬坡时间约束[8](式(9)),即:

需要说明的是,式(9)为AGC 机组持续上爬坡(增加出力)时间约束,持续下爬坡(减少出力)时间约束类似。
此外,AGC 机组功率增减指示变量还需满足以下约束,以确保增减出力状态互斥:
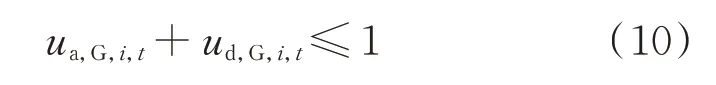
1.2.3 AGC 机组控制性能约束
AGC 机组控制性能相关约束包括频率偏差约束(式(11))、联络线功率偏差约束(式(12))、控制性 能 标 准1(control performance standard 1,CPS1)指标约束[9,17](式(13)至式(15)),以及CPS2 指标约束(式(16))。


2 AGC 动态优化调度模型的转化与处理
前述AGC 机组动态优化调度模型(记为M0)是MINLP 模型,其非线性源自目标函数(式(1))的绝对值项、描述AGC 机组出力(式(5))和CPS1 指标(式(14))的2 个等式约束以及式(2)中的功率损耗Ploss,t。
对于目标函数,引入辅助变量ZG,i,t[18]:
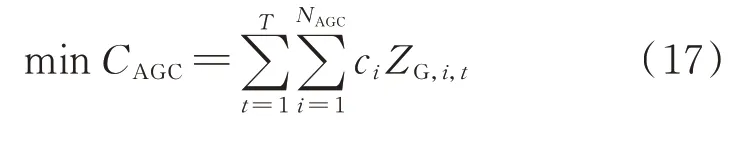

由于AGC 调度模型为最小化优化模型,且ci>0,易知式(17)和式(18)与式(1)等价。
2.1 双线性项的处理
式(5)和式(14)的非线性项均为2 个变量乘积形式,即“双线性项”。其中,式(5)的双线性项(ua,G,i,t-ud,G,i,t)RG,i,t为0-1 变量与连续变量的乘积,而式(14)中EACE,tΔFt为2 个连续变量的乘积。本文根据两双线性项的不同特点,分别采用变量替换及分段McCormick 包络技术进行处理。
变量替换是化简和转化数学模型的常用手段,在配电网DistFlow 模型[19-20]及天然气系统管道流量方程的处理中均有应用[21],本文结合式(5)中0-1 变量的物理意义,通过变量替换处理式中的双线性项。
McCormick 包络是优化问题中处理双线性项的一种常用方法,其基本思想是用一组线性约束松弛原双线性项的可行域[22],分为单变量分段[23-24]和双变量分段McCormick 包络[25-26]等。目前,在电力系统优化调度问题中已有应用[27]。本文采用双变量分段McCormick 包络处理式(14)中的双线性项EACE,tΔFt。
2.1.1 AGC 机组出力约束的处理

2.1.2 CPS1 指标约束的凸松弛
对于CPS1 指标(式(14))的双线性项,本文采用分段McCormick 包络技术[26]进行凸松弛处理。
首先,引入辅助变量ωCPS1,t替换EACE,tΔFt:

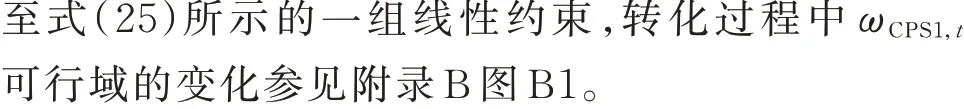
2.2 功率损耗的处理
本文基于功率损耗因子[15]对式(2)中的功率损耗Ploss,t进行处理。假设区域电网各节点电压标幺值为1.0,则功率损耗可由下式近似:

式中:Ploss,0,t为t时段与泰勒展开点功率损耗值相关的常数;Pt为t时段节点注入功率列向量;Lt为t时段功率损耗因子行向量;Pm,0,t和Pb,0,t分别为t时段对应泰勒展开点的支路m传输功率和节点b注入功率;lb,t为时段t节点b的功率损耗因子,是Lt的元素。
式(27)是式(26)的线性近似,其近似精度与泰勒展开点的选取有关。为减小近似误差,本文根据AGC 调度结果不断更新泰勒展开点,从而实现Ploss,0,t和Lt的 迭 代 修 正。
3 AGC 动态优化调度模型的双层迭代算法
3.1 双层迭代算法的基本流程
通过上述处理,AGC 机组动态优化调度的原模型(M0)可转化为以下MILP 模型:目标函数为式(17);约束条件由式(2)至式(4)、式(6)至式(13)、式(15)、式(16)、式(18)、式(20)、式(21)、式(23)至式(25)及式(27)组成。
将原模型转化为MILP 模型能够提高模型的求解效率,但双线性项的凸松弛和功率损耗的线性近似均会引入计算误差。本文进一步提出一种双层迭代算法以提高模型求解精度。
关于双线性项的凸松弛,假设对原模型M0 目标函数绝对值项和AGC 机组出力进行等效变换(参见式(17)至式(21))及功率损耗线性化(式(27))处理后所得模型为M1,则M1 仍为MINLP 模型,但其非线性仅源自双线性项EACE,tΔFt。进一步应用分段McCormick 包络技术处理该双线性项,则M1 松弛为MILP 模型(记为M2)。另一方面,若将M1 的整数变量固定为对应取值范围内的某个值,则M1转化为不含整数变量的NLP 模型(记为M3)。M1至M3 可行域的示意图见图1。
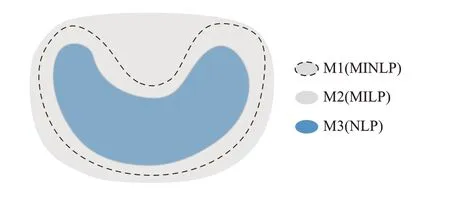
图1 可行域韦恩图Fig.1 Venn diagram of feasible region
记M1 至M3 最优解的目标函数值分别为CAGC,M1、CAGC,M2、CAGC,M3, 则CAGC,M2≤CAGC,M1≤CAGC,M3。因此,若能使M2 和M3 优化解足够接近,则可以认为M2 或M3 的解可以较为精确地近似M1[24]。由 于M2、M3 分 别 为MILP 模 型 和NLP 模型,两者的求解难度较M1 大大降低;此外,M2 的解可以为M3 提供一个较好的初值,而M3 的解又可以作为参考值来帮助M2 缩小双线性变量取值范围以减小松弛间隙,因此,通过反复求解M2 和M3,可以提升M1 的求解精度。
关于功率损耗,由式(27)和式(28)可见,其计算精度与泰勒展开点的选取有关。为此,本文根据优化结果不断修正展开点,以提高功率损耗的计算精度。
综上,本文提出一种双层迭代算法,内层循环实现M2 和M3 的迭代求解、外层循环实现功率损耗计算参数的迭代更新,基本流程如图2 所示。
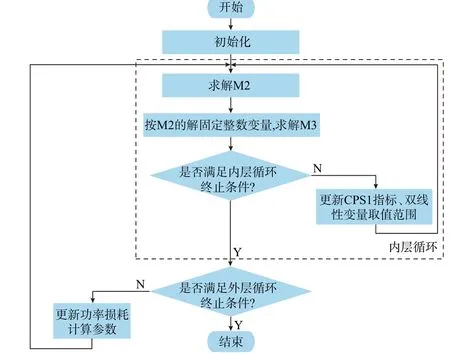
图2 所提算法流程Fig.2 Flow chart of proposed algorithm
3.2 CPS1 指标的迭代计算(内层循环)


图3 双线性项迭代示意图Fig.3 Schematic diagram for iteration of bilinear term
更新EACE,t和ΔFt的取值范围后,再于第p+1次迭代时,根据式(24)和式(25)对双线性项进行分段McCormick 包络处理(分段数不变)。可见,在内层循环迭代过程中,通过M2 和M3 的反复求解,EACE,t和ΔFt的范围不断缩小,M2 的松弛间隙及M2与M3 目标函数值差距(CAGC,M3-CAGC,M2)也将随之减小。
按式(30)计算优化间隙G,当G小于收敛精度e1时,停止内层迭代。
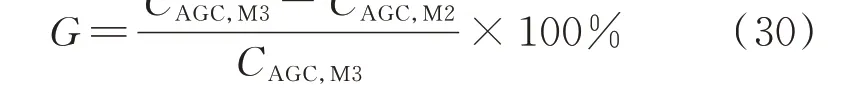
由式(29)可见,内层迭代过程中EACE,t和ΔFt的范围不断缩小,迭代次数足够多即可保证收敛;为避免迭代次数过多而影响AGC 调度模型的求解效率,同时设置最大迭代次数。由于内层循环退出时M2仍然有一定的松弛间隙,本文取M3 的解作为内层循环的最终优化解,并以此更新功率损耗的计算参数。
需要指出,虽然式(29)能够有效缩小M2 与M3目标函数值的差异,但难以保证更新后的区域一定涵盖M1 的最优解。即便如此,由于本文采用精度较高的分段McCormick 包络,依然能够保证内层迭代最优解的精度。
3.3 功率损耗的迭代计算(外层循环)
外层循环利用前一次优化结果更新功率损耗计算 参 数[16],对 第g次 迭 代,按 式(31)更 新Ploss,0,t及lb,t:

关于功率损耗计算,作以下说明:
1)外层循环的实质是利用前一次迭代的优化结果修正功率损耗泰勒展开点以减少线性化误差,基本思想为优化理论中的序贯线性规划算法[28]。
2)为了考虑网络功率损耗对支路功率的影响,需将功率损耗作为等效负荷记入节点注入功率。以外层循环第g次迭代为例,节点b注入功率[29]为:



外层循环以相邻2 次外层迭代所得M3 目标函数(即CAGC,M3)的相对偏差小于给定精度e2为终止条件。本文同样设置外层循环最大迭代次数以保证调度模型的求解效率。若外层循环超过最大迭代次数,则以前一次外层迭代过程中内层迭代终止时M3 的解作为最终优化结果。为改善外层循环的收敛性,可以在式(31)的基础上,同时利用前2 次迭代结果更新泰勒展开点(详见附录C)。
4 算例分析
采用IEEE 14 节点系统和IEEE 57 节点系统算例验证本文方法。两个算例的优化模型规模见附录D 表D1、详细数据见文献[31]。本文基于MATLAB分别调用Gurobi 及Ipopt 求解器求解所提算法中的MILP 模型(M2)和NLP 模型(M3);运行环境为Intel Core i7-10750H 2.6 GHz CPU、16 GB 内存笔记本电脑。
4.1 不同求解方法对比
为验证所提算法的有效性,基于IEEE 14 节点系统,对比以下3 种求解方法:
方法1:调用MINLP 求解器SCIP 直接求解原模型M0。其中,功率损耗等式约束采用式(26)所示的非线性方程。
方法2:基于文献[3,9-11]的进化规划算法直接求解原模型M0,功率损耗计算同方法1。
方法3(本文方法):基于本文所提算法求解模型M0(EACE,t和ΔFt的分段数均设置为15)。
算例系统的净负荷(实际负荷功率扣除风电功率)曲线如图4 所示。
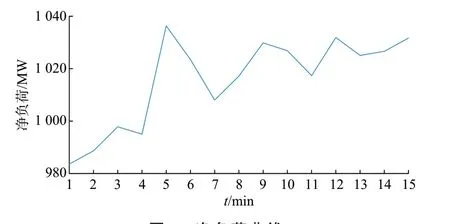
图4 净负荷曲线Fig.4 Curve of net load
应用3 种方法对AGC 机组进行调度,优化结果如表1 所示。表中,“成本相对偏差”以方法1 的AGC 调节成本为参考,为正表示所得调节成本大于方法1;方法2 的调节成本和计算时间为120 次优化计算的最小成本及平均用时。
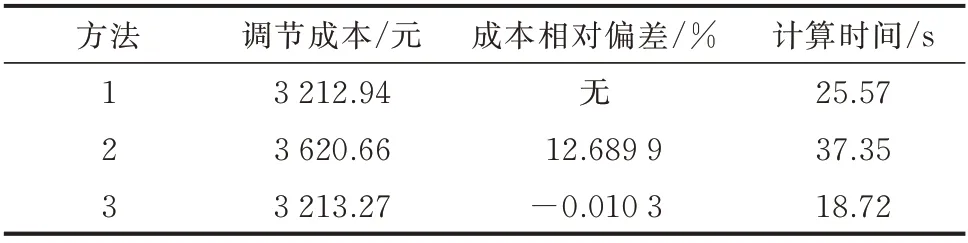
表1 3 种方法的优化结果及计算时间Table 1 Optimization results and computation time of three methods
由表1 可见,本文方法与参考方法(方法1)相比的相对偏差仅为0.01%,计算精度显著高于方法2(成本相对偏差约13%);此外,本文方法用时最短,与方法1 相比减少约30%,与方法2 相比,减少约50%。以上结果表明,与文献[3,9-11]的进化规划方法比较,本文方法具有明显的精度和速度优势。
本文方法的迭代过程如图5 所示,图中同时给出SCIP 求解原模型M0 所得调节成本和功率损耗。由图5 可见,外层循环迭代4 次、每次外层迭代含3 次内层迭代。在迭代过程中,M2 的调节成本始终低于M3,与前述理论分析一致;对于每次外层迭代的第1 次内层迭代,M2 和M3 调节成本均比较接近,而随着内层迭代次数增加,两者的差距明显减小。除第1 次外层迭代基于功率损耗初始值(常数)求解M2 和M3 导致两者调节成本与M0 偏差较大之外,其后各次外层迭代的第1 次内层迭代,M2 和M3 的调节成本都比较接近M0,表明仅1 次内层迭代就能在一定程度上保证M2 和M3 的求解精度;此后,随着内层迭代次数的增加,M2 和M3 的调节成本都趋近于M0,表明内层迭代提升了M2 和M3 的求解精度。
此外,由图5(a)可见,随着外层迭代次数的增加,M3 与M0 调节成本的偏差进一步缩小。由图5(b)可见,第1 次外层迭代功率损耗约34.5 MW,与M0 功率损耗的偏差约为5%,表明初始展开点具有较高精度;第2 次外层迭代结束时,线性化功率损耗的精度明显改善(与M0 的偏差仅为0.2%);此后,随着外层迭代次数的增加,线性化损耗进一步趋近M0,表明外层迭代能够有效减少功率损耗的线性化误差。

图5 所提方法的迭代过程Fig.5 Iterative process of proposed method
综合图5(a)及图5(b)可见,内层迭代能够有效降低M2 和M3 的差距,外层迭代能够有效减少功率损耗的线性化误差,两者共同保证了AGC 调度模型的求解精度。
4.2 对不同负荷工况的适应性
为验证本文方法对不同负荷工况的适应性,以图4 净负荷曲线为基础,设置如表2 所示的6 种净负荷变动场景(各场景的净负荷曲线详见附录D图D1)。

表2 6 种负荷变动场景Table 2 Six scenarios of load variations
应用方法1 和本文方法分别对6 种场景下的AGC 机组优化调度模型进行求解(EACE,t和ΔFt的分段数均设置为15),各场景的优化结果及计算时间如表3 所示。其中,“成本相对偏差”以方法1 的调节成本为参考;“最大功率损耗偏差”为式(27)所得功率损耗相对于式(26)的偏差(取各时段相对偏差的最大值),可评估功率损耗线性近似的精度。

表3 6 种场景的优化结果Table 3 Optimization results of six scenarios
由表3 可见,由于场景1 至场景4 的负荷按基础负荷水平成比例变化,因此,随负荷水平增加,净负荷波动幅度随之增加,导致AGC 调节成本相应增加。场景5 模拟负荷下降场景,其负荷波动情况与场景3 一致(见附录D 图D1),AGC 调节成本也与之相当。场景6 通过不同程度降低场景3 中各时段的负荷变化幅度来模拟负荷缓变场景,负荷波动幅度小于场景3 和4 而大于场景1 和2,其AGC 调节成本也介于两者之间。在各种场景下,最大成本相对偏差小于0.03%,而最大功率损耗偏差小于0.004%,表明本文方法在各种负荷波动场景下均能保证很高的计算精度;在计算时间方面,各场景平均用时约20 s,最长用时不到30 s,能够满足AGC 优化调度要求。
为进一步验证本文方法对持续负荷变化的适应性,基于美国宾夕法尼亚-新泽西-马里兰(PJM)超短期负荷预测数据[32]构造日净负荷曲线(见附录D图D2),以96 点日前计划(间隔15 min)为基础,对算例系统的AGC 机组进行优化调度。结果显示,对于全天96 个时段AGC 调度模型而言,外(内)层循环迭代次数均为3(2);全天AGC 机组调节成本的最大偏差小于0.03%、最大功率损耗偏差约0.01%;平均用时低于20 s、最长耗时约25 s(见附录D 表D2)。
以上结果表明,本文方法对不同负荷工况具有良好的适应性。
4.3 双线性项McCormick 包络分段数的影响
以IEEE 57 节点系统为算例[31]进一步验证本文方法对更大规模算例的适应性,并讨论McCormick包络分段数对本文方法性能的影响。
基于方法1 求解IEEE 57 节点系统算例,AGC机组的调节成本为6 774.21 元,计算用时259.75 s。本文方法在不同分段数设置方案下的优化结果如表4 所示(EACE,t和ΔFt的分段数设置相同)。可见,各种分段数下,本文方法的调节成本与方法1 基本一致,而平均用时仅为方法1 的10%。与IEEE 14节点系统算例(平均用时约20 s)比较,本算例的计算时间有一定增加,但幅度不大,表明本文方法对于较大规模算例仍具有良好的计算精度和速度。
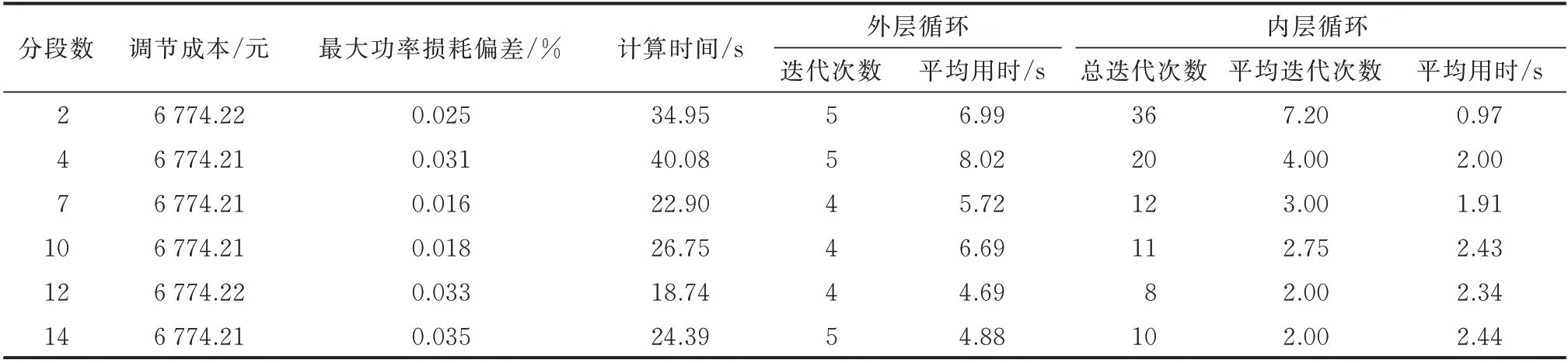
表4 不同双线性变量分段数设置下的计算结果Table 4 Calculation results with different segment number settings of bilinear terms
进一步分析分段数对内、外层循环的影响可见:一方面,随分段数增加,内层平均迭代次数减少,但平均用时增加,这是因为分段数增加使得相同迭代次数下McCormick 包络的松弛间隙以及M2 与M3之间的优化间隙相应减少,内层循环迭代次数随之减少;另一方面,分段数增加导致McCormick 包络的整数变量及约束条件增多,M2 的计算规模增加,内层循环求解M2 的时间相应增加。外层迭代更新功率损耗计算参数,受分段数影响小。此外,由于外层迭代的终止判据为相邻2 次迭代的目标函数相对偏差足够小(参见3.3 节),分段数设置对AGC 机组最终调度结果的影响较小,但会影响内层循环的迭代次数和计算时间,从而影响整个优化计算的时间。
需要特别指出,本文算法所处理的双线性项(EACE,tΔFt)数量仅与调度时段有关,而与系统规模无关。因此,对于不同规模的系统,同样的分段数会引入相同数量的整数变量,尽管分段数增加会在一定程度上增加M2 的整数变量,但整数变量的数目并不会随系统规模增大而增加。这一特点也表明本文算法对大规模系统具有良好的适应性。
5 结语
本文基于双线性项的分段McCormick 包络和功率损耗的线性化,将AGC 机组动态优化调度的原模型转化为可高效求解的MILP 模型,并进一步提出内层循环收紧双线性项松弛间隙、外层循环减小功率损耗线性化误差的双层迭代算法。得到以下结论:
1)与现有AGC 机组动态优化调度模型广泛采用的进化规划算法比较,本文方法在计算精度及速度方面具有明显优势。
2)对不同负荷变动场景,本文方法均能高效求解AGC 机组调度模型,对工况变化适应良好。
3)McCormick 包络分段数对AGC 机组最终的调度决策影响较小,表明本文方法对分段数的适应性较强;但不同分段数会在一定程度上影响本文方法的计算时间。
后续将改进分段McCormick 包络的变量更新策略,并进一步研究AGC 机组随机调度模型的高效求解方法。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
