计及故障场景集的风光储混合系统区域无功储备多目标优化
2022-09-19陈光宇吴文龙戴则梅徐晓春张仰飞郝思鹏
陈光宇,吴文龙,戴则梅,徐晓春,张仰飞,郝思鹏
(1. 南京工程学院电力工程学院,江苏省南京市 211167;2. 南瑞集团有限公司(国网电力科学研究院有限公司),江苏省南京市 211106;3. 国网淮安供电公司,江苏省淮安市 223400)
0 引言
无功储备是电力系统实现安全稳定的重要保障,对无功储备进行优化是提高电网安全水平的有效手段[1]。近年来,随着新能源渗透率的不断增加,传统火电机组开机减少,电网运行机理正发生改变,电压控制难度加大。因此,利用风电、光伏、储能等多类型可调资源参与电网无功电压协调控制,充分发挥多类型可调资源的无功调节能力,提高区域电网故障场景下的无功储备水平,对电网安全稳定运行具有重要意义。
在无功储备定义方面,传统无功储备被定义为:无功源最大无功出力与当前无功出力之差[2]。但该定义对系统无功储备估计过于乐观,为更准确地衡量系统总无功储备,部分学者将无功储备进一步定义为:各个无功源无功储备的加权之和[3]。近年来,随着电网规模的不断壮大,电网无功电压区域耦合特性备受关注,而无功储备对节点电压的支撑能力被认为是无功储备的核心。因此,基于分区的大电网无功储备计算正逐渐得到更多研究人员的青睐[4]。
在无功储备优化领域,文献[5]通过优化系统的发电机无功储备提高系统静态电压稳定裕度,构建了以系统无功储备最大化为目标的优化模型,并采用Benders 分解加速求解。仿真结果表明,该方法能有效提高系统电压稳定裕度。文献[6]提出了一种基于电压分区的区域发电机无功储备定义,建立了区域发电机无功储备优化的模型。仿真结果表明,分区优化方法在计算效率和容错率上都优于整体优化方案。以上文献对传统电网无功储备优化的建模和求解进行了深入研究,但随着风电等新能源占比的逐年增加,新能源出力的随机性对电网的影响已不容忽视。近年来,新能源背景下的电网无功储备问题得到了众多学者和研究人员的关注。针对风电的不确定性问题,文献[7]采用一种新的无功储备评估方法,并提出电力系统随机无功储备优化模型,该方法有效降低了新能源背景下系统的运行风险。文献[8]提出了一种考虑发电机重调度的区间最优无功储备优化模型,采用间隔模型描述新能源的不确定性,算例表明该方法对新能源的不确定性表现出更好的稳健性。此外,传统的无功储备优化以确定型的负荷增长方式为基础,而新能源的随机性对负荷增长方式的确定具有负面作用。因此,文献[9]建立了无功储备两层优化模型,采用内外层迭代求解无功储备问题,结果表明该方法可在考虑负荷增长不确定性时提升系统的无功储备水平。
以上文献对新能源接入背景下的无功电压问题进行了深入探讨,并取得了较好的效果。但研究大多只考虑了新能源并网后正常工况下的无功电压问题。随着特高压直流输电的发展,受端电网直流馈入下的区域无功储备不足问题日益突出。当系统发生故障时,传统电网无功储备及优化方案难以支撑电网安全稳定运行。因此,为了提高故障下区域电网无功储备,应对故障下电压稳定裕度不足等情况,研究故障下区域无功储备优化问题具有重要的理论和实际意义。
针对以上问题,本文在前述研究的基础上,考虑通过深挖风光储等多类型资源的无功调节能力,构建故障下区域无功储备优化模型,进一步提高故障下电网电压安全水平。基于这一思想,本文提出了一种计及故障场景集的风光储混合系统区域无功储备多目标优化方法。首先,提出一种考虑新能源波动性的典型故障场景缩减方法,基于有效无功源筛选策略构建故障场景的特征向量,在此基础上建立典型故障场景集,实现对故障场景的降维。其次,给出一种基于改进聚类算法的电网分区方法,进一步降低问题的维度,提高求解效率,从空间角度对模型进行降维。最后,提出一种基于典型故障场景的分区无功储备优化方法,构建故障下区域无功储备多目标优化模型,采用改进多模态多目标进化算法(下文简称MMEA-NSGA-Ⅱ)得到Pareto 前沿,并通过模糊理论得到折中最优解,实现对故障下电网电压稳定裕度的提高。算例采用IEEE 39 系统和真实电网进行仿真分析。仿真结果表明,本文提出的故障下区域无功储备优化方法能够有效提高故障下系统的电压安全水平,降低系统的运行风险。
1 无功储备计算
故障场景和无功源自身状态的变化都将对区域内电压的稳定性产生影响。本章通过对电网稳态场景下不同类型可调资源的无功储备计算,得到故障下区域无功储备。
1.1 多类型资源无功储备计算方法
1.1.1 风电场无功储备
随着由双馈风电机组成的风电场接入电网的数量不断增加,该类风电场的可调无功资源可充分利用。对于大型风电场,本文采用风电场集总模型[10],整个风电场的无功储备如式(1)所示。

式中:QWF,res为风电场无功储备;Qgres,g为第g台风电机组提供的无功容量;n为该风电场内的双馈风电机组数。
1.1.2 分布式光伏无功储备
通常,光伏系统都以最大功率发电,可调节其功率因数参与无功调节。光伏系统的无功储备表达式[11]为:

式中:PPV,j和QPV,j分别为节点j注入的光伏有功和无功功率;QPV,max,j为节点j处光伏的无功调节范围上 限;QPV,res,j为 节 点j处 光 伏 的 无 功 储 备;SPV,j为 节点j处的光伏逆变器容量。
1.1.3 储能系统无功储备
单时间断面下储能系统的无功储备表达式[12]为:

式中:PESS,j为储能系统在节点j处注入的有功功率,PESS,max,j为其上限;QESS,j为节点j处储能系统可注入的 无 功 出 力,QESS,max,j为 其 上 限;QESS,res,j为 节 点j处储能系统的无功储备;SESS,max,j为节点j处储能系统逆变器的最大视在功率。
1.2 故障下区域无功储备计算方法
本文通过选取合适的主导节点以反映所处区域电压稳定程度。在此基础上,通过故障场景下该区域内无功源对主导节点的电压支撑能力表示故障下区域无功储备。
故障场景k下区域无功储备Qkr,RES的表达式为:

式中:Qkri,res为故障场景k下区域电网r中无功源i的无功储备;Nr为区域电网r中无功源数目;kkri为故障场景k下区域电网r中的无功源i对区域电网r主导节点的无功/无功灵敏度[13],用以表征无功源的无功储备对区域电网电压安全的贡献度。
2 考虑新能源波动性的典型故障场景缩减
由于新能源的波动性,电网故障扫描产生的故障集通常较为庞大,给优化计算带来不便[14]。为提高无功储备优化的效率,本文提出一种考虑新能源波动性的典型故障场景缩减方法。首先,对全场景集进行场景缩减得到典型场景集。其次,构建电压关联指标以筛选出有效无功源,基于场景内有效无功源无功储备构建场景特征向量,并通过预想故障扫描得到故障场景集,根据场景特征向量进行聚类,得到各类故障场景集。最后,根据电压稳定指标从场景集中筛选出典型故障场景。典型故障场景缩减的整体框架如附录A 图A1 所示。
2.1 基于场景间相似度的典型场景集生成策略
新能源的波动性导致全场景集的规模十分庞大,本节从多类型资源无功储备中提取特征,通过计算不同场景间的相似度,对全场景集进行场景缩减[15],最终得到典型场景集,具体步骤如下:
1)根据上文的多类型资源无功储备指标,将不同场景下多类型资源无功储备映射为标量,由无功储备Qxres构成该场景的特征向量QFitzxres,表达式为:
2)采用欧氏距离计算故障场景间的相似度;相似度计算示意图如附录A 图A2 所示。
3)根据相似度对全场景集进行场景缩减,得到典型场景集。
2.2 基于电压关联指标的有效无功源筛选策略
通过衡量无功源个体在电网中的“地位”(即无功源对电网电压的无功调节能力),筛选出对薄弱节点电压影响较大的有效无功源,以减少场景特征向量的维数,提高计算效率。具体步骤如下:
1)采用电网薄弱环节辨识方法[16]辨识出故障下电网的薄弱节点;
2)计算电网内无功源对薄弱节点的电压/无功灵敏度α,得到电压/无功灵敏度集合K;
3)采用最大类间方差(OTSU)算法对电压/无功灵敏度集合K进行分割,得到分割阈值kth;
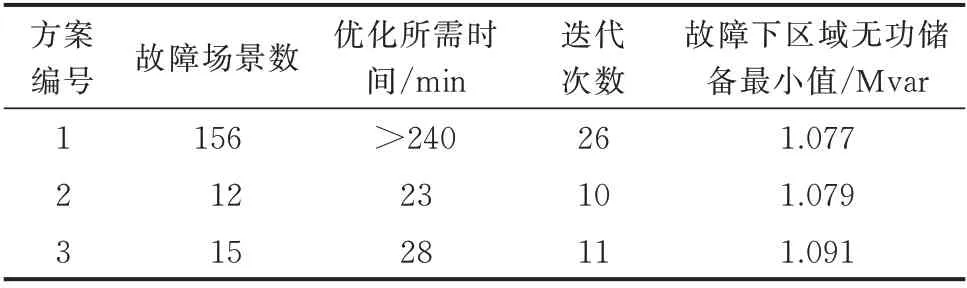
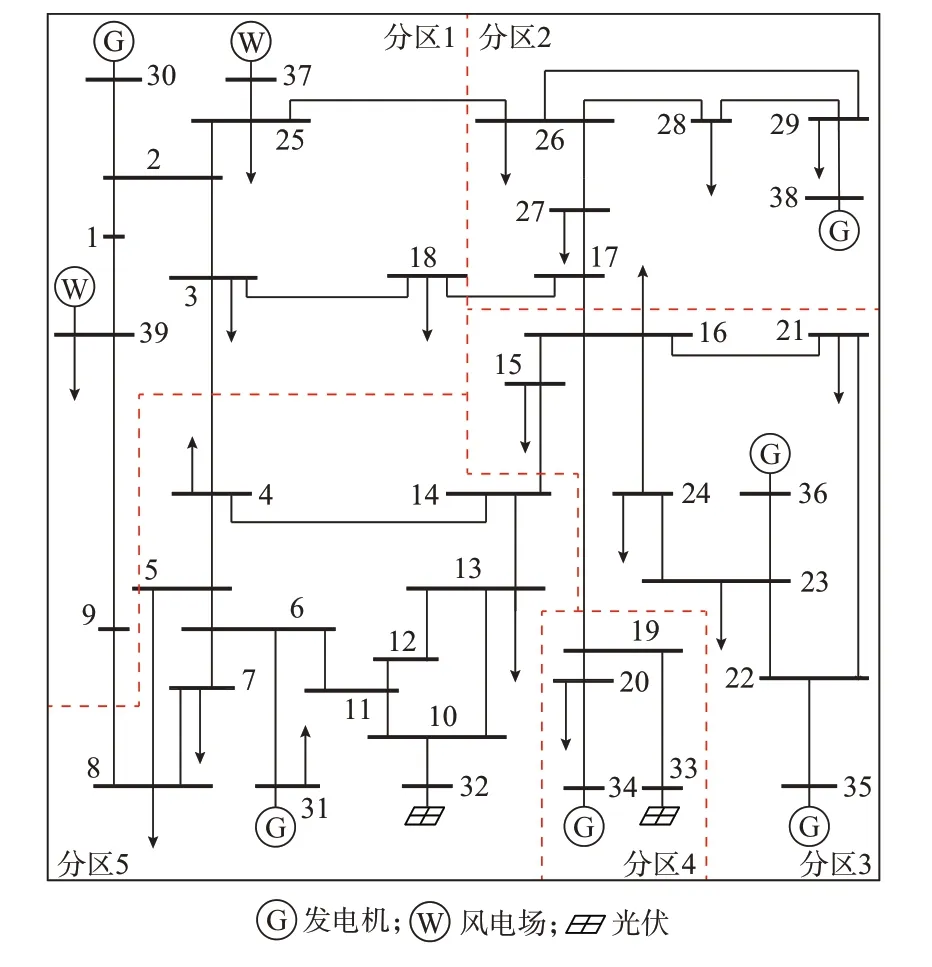
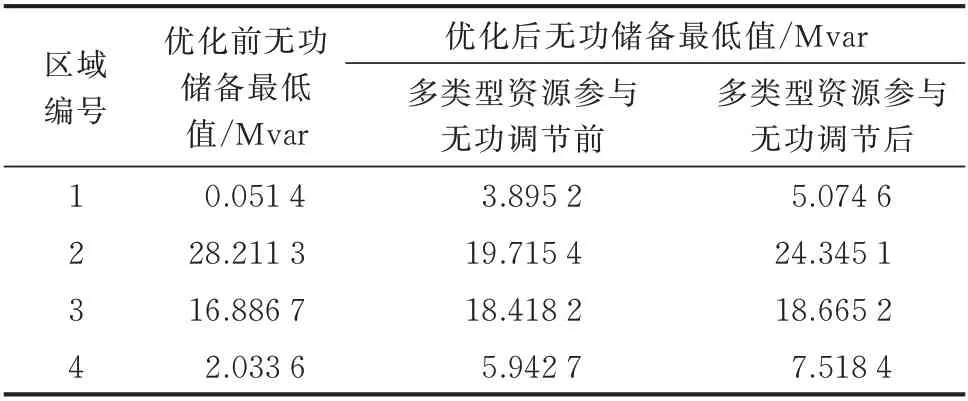
4)基于分割阈值kth判断无功源与薄弱节点间是否存在关系,若α≥kth,则判断无功源与节点间存在关系;若α 5)基于无功源与节点间关系,得到电压关联指标集合; 6)基于电压关联指标筛选出所有薄弱节点的有效无功源; 7)将所有薄弱节点的有效无功源聚合,得到电网的有效无功源集合。 2.2.1 考虑新能源波动性的灵敏度计算 在风光储混合电网中,计算节点间的电压/无功灵敏度需考虑新能源波动性的影响。因此,本文引入修正系数[17]计算典型场景下节点间的电压/无功灵敏度,量化新能源波动对于灵敏度的影响。 薄弱节点m对无功源i的电压/无功灵敏度的计算公式为: 式中:kim为考虑新能源波动性下节点m对无功源i的电压/无功灵敏度;kiwm为在典型场景w下节点m对无功源i的电压/无功灵敏度;λiw为无功源i在典型场景w下的修正系数;Kd为典型场景数目。 2.2.2 基于OTSU 算法的分割阈值计算 本文引入OTSU 算法对无功源与节点的电压/无功灵敏度进行分割,以得到用于判断无功源与薄弱节点的电压之间是否存在关系的分割阈值。具体流程如附录B 所示。 2.2.3 电压关联指标构建 根据分割阈值kth可判断无功源i与薄弱节点m的电压之间是否存在关系,得到无功源电压关联指标,如式(7)所示。 式中:Xim为0-1 变量,表示无功源i与节点m的电压之间是否存在关系,存在关系则取1,否则取0。 2.2.4 有效无功源筛选 计算无功源电压关联指标,筛选出薄弱节点m的有效无功源,有效无功源集合SmNy的表达式为: 式中:SN为无功源的集合。 将所有薄弱节点的有效无功源集合聚合,得到该电网的有效无功源集合SNy。 对于预想故障扫描所得的故障场景集,受限于极大的场景数目,需要对数据信息进行提取。本文首先根据有效无功源的无功储备构建故障场景特征向量,并引入t分布-随机邻近嵌入(t-distributed stochastic neighbor embedding,t-SNE)算法对特征向量进行降维。其次,采用层次聚类方法将故障场景集划分为若干个子场景集。最后,基于邓恩指数(Dunn validity index,DVI)对聚类方案进行评价,得到最佳聚类方案。 2.3.1 场景特征向量 在不同故障场景下,系统电压和电网结构都会发生变化,为维持电网电压稳定,无功源会受到影响,其无功储备发生变化。因此,本节采用2.1 节方法,根据有效无功源的无功储备构建故障场景k的特征向量。 2.3.2 场景特征向量降维 为去除特征向量集噪声并在低维空间内反映样本特性,本节引入t-SNE 算法对故障场景特征向量进行降维。具体步骤如附录C 所示。 故障集内各断面对无功储备的影响较为相似,因此,在故障下进行区域无功储备优化时,仅需考虑故障场景集中典型场景的作用。本文引入局部电压稳定指标[18]以构建故障场景下电网的电压稳定指标,通过对各类故障场景集中的场景进行评估,筛选出典型故障场景。 故障场景k的电压稳定指标Lk为: 式中:Styp为典型故障场景集;Sq为故障场景集中的第q个典型故障场景;A为典型故障场景数,该数值等于最佳聚类数。 在无功储备优化前进行分区可以提高求解效率,降低解决问题的难度[19]。因此,以第2 章典型场景为基础,本文构建考虑新能源波动性的主导节点控制空间,将基于密度的有噪空间聚类(DBSCAN)算法与K-means 聚类算法有机结合形成改进聚类算法(下文简称改进D-K 聚类算法)[20],给出一种基于改进聚类算法的电网分区方法。 基于改进D-K 聚类算法的电网分区过程主要分为主导节点控制空间构建和基于改进D-K 聚类算法的电网分区,具体流程如附录D 图D1 所示。 为表征新能源波动导致电网节点间电压灵敏度的变化情况,本文引入考虑新能源波动性的电气距离期望矩阵[17],在此基础上构建主导节点控制空间。 计算电气距离期望矩阵D,公式如附录D 式(D1)所示。选取D中元素构建主导节点控制空间。对于电网节点j,根据电气距离期望矩阵,构建表示该主导节点对负荷节点的控制能力的向量lj: 式中:djl为电气距离期望矩阵D中第j行第l列的元素,即电网节点j与负荷节点l之间的电气距离;Nl为电网中负荷节点的数量,考虑到新能源的无功调节能力,新能源所在节点不作为负荷节点参与本节划分。 在此基础上获得主导节点控制空间L=[l1,l2,…,lN],是一个N维的坐标空间,由表示主导节点对负荷节点控制能力的列向量lj组成,行向量表示电网中负荷节点受不同主导节点的电压控制能力的影响程度。主导节点控制空间L包含主导节点对于负荷节点电压调节的相关信息。 由于传统K-means 聚类算法得到的聚类结果波动性较大。因此,本文引入改进D-K 聚类算法[20]进行电网分区,并通过OTSU 算法对密度聚类部分进行改进,在获取初始聚类中心等参数后,通过Kmedoids 聚类算法进行进一步的聚类分析。 基于主导节点控制空间,计算任意两节点间的平均距离、每个节点的密度参数和平均类间最大相似度(average inter-class max similarity,AMS)指标。 采用2.2.2 节中的OTSU 算法,根据密度参数将节点划分为两部分,选取密度参数大的部分加入备选集E。从备选点集E中选择点作为初始聚类中心,经过划分后计算此时的AMS 值,通过比较AMS值,不断更新聚类中心以确定最佳聚类数目o,以此时的o个聚类中心作为K-medoids 算法的初始聚类中心对电网进行分区,最终得到电网中负荷节点分区方案。 以上文所得典型故障场景集和电网分区方案为基础,为提高故障下电网电压稳定性和区域内主导节点对负荷及无功源节点的电压控制能力。本章建立了以典型故障场景下区域无功储备最大化和区域电网内主导节点可控性最大化为目标的多目标优化模型,采用模糊理论融合MMEA-NSGA-Ⅱ进行求解。图1 展示了故障下区域无功储备优化流程。 图1 故障下区域无功储备优化流程图Fig.1 Flow chart of regional reactive power reserve optimization with fault 4.1.1 目标函数 1)典型故障场景下区域无功储备目标 在稳态运行期间,为电网预留充足的无功储备有利于电网的安全稳定运行,且考虑到无功功率分层分区平衡的要求,电网任意区域的区域无功储备不足可能会导致系统失稳。因此,当故障场景下各分区中区域无功储备最小值较大时,可以保证各区域内故障下电压稳定裕度较大。根据第1 章中故障下区域无功储备定义建立指标,表达式如下: 式中:kqri为典型故障场景q下区域电网r中无功源i无功储备的修正系数,用以表征多类型可调资源无功储备对系统主导节点电压安全的贡献度;Qqi,res为典型故障场景q下动态无功源i的无功储备。 2)区域主导节点对其内部节点的可控性目标 本文中,区域无功储备的计算是通过以故障下无功源对主导节点的无功/无功灵敏度为权重因子来获得的。因此,选择的主导节点需要最大程度反映电网该区域内的电压稳定程度,本文根据区域内主导节点的可控性建立指标。 区域主导节点可控性目标指分区主导节点对其内部负荷或无功源节点的最小电压/电压灵敏度,当该目标充分大时,可以保证分区主导节点对区域内所有负荷和无功源节点的电压控制能力充分强。主导节点可控性指标表达式为: 式中:Tr为区域电网r中负荷或无功源所在节点集合;αrj为区域电网r主导节点对节点j的电压/电压灵敏度,根据1.2 节中方法获得;NA为电网中区域电网数目。 4.1.2 约束条件 约束条件包括区域内无功平衡、区域内部无功源数量约束、区域耦合等条件。 1)区域内部无功源和负荷节点的数量约束:要求区域电网内的无功源和负荷节点数量都必须分别大于等于1。 2)各分区的连通性约束:区域电网内各节点具有连通性。 3)变量约束:稳态情况下的潮流约束、电压约束等约束条件如附录E 式(E1)所示。 由于缺乏对于决策空间多样性的维护,传统多目标优化算法在求解多模态多目标优化问题时性能较差。因此,本文提出一种改进多模态多目标优化进化算法对多目标优化模型进行求解,算法以带精英策略的非支配排序遗传算法(non-dominated sorting genetic algorithms-Ⅱ,NSGA-Ⅱ)为基础,通过引入加权指标和收敛空间[21]进一步提高种群的多样性和逼近Pareto 最优前沿,考虑到加权指标计算量较大,给出一种两阶段自适应群体更新策略以提高收敛效率,通过模糊理论选取折中最优解。MMEA-NSGA-Ⅱ框架如附录E 图E1 所示。 4.2.1 加权指标 为了保证决策空间多样性和目标空间收敛性之间的平衡,引入加权指标以评估解决方案的潜在收敛质量,该指标可以保证解决方案分布在多个最优解而非一个最优解。 通过使用个体所有解的指标之和以及个体到其他所有个体在决策空间中的欧氏距离,获得个体的加权指标。加权指标的表达式见附录E 式(E2)。 4.2.2 收敛空间 为了逼近Pareto 最优前沿,提高目标空间的收敛性,采用收敛空间以存储已获得的非支配解,引入改进拥挤距离以更新收敛空间,从而平衡每个目标值对应的等价解数量。改进拥挤距离的表达式如附录E 式(E3)所示。 当收敛空间中解的数目超过规定的数值后,计算收敛空间中全部解的改进拥挤距离,选择拥挤距离大的解组成新的收敛空间。 4.2.3 两阶段自适应群体更新策略 为了保证算法的收敛效率和决策空间的多样性,给出一种两阶段自适应群体更新策略,采用自适应算子以提高不同阶段下算法的全局和局部搜索能力。 群体更新策略分为两个阶段: 1)第1 阶段,当收敛空间中解集数小于所需的Pareto 解集数目时,从决策空间中选择父代。在该阶段对解的加权指标进行评估以保持决策空间中解的多样性。为提高搜索全体解,接近Pareto 最优解的速度,该阶段采用较大的交叉概率。自适应交叉算子的表达式如附录E 式(E4)所示。 2)第2 阶段,当收敛空间中解集数大于等于所需的Pareto 解集数目时,根据概率p从收敛空间中选择父代,将收敛空间中父代与决策空间中父代合并形成新的父代。更大的概率p易导致更好的收敛性,但解的多样性会变差。一般情况下p为0.4。为了避免陷入局部最优的问题,该阶段采用较大的变异概率。自适应变异算子的表达式如附录E 式(E5)所示。 4.2.4 基于模糊理论的最优解选取 为了更客观且全面地做出决策,通常需要全面考虑各方面的因素以充分挖掘Pareto 中所包含的信息。本文采用模糊理论计算目标的隶属度函数,以反映目标函数最大值和最小值之间的相对距离,获得一个相对最优的Pareto 最优解[22]。Pareto 最优解集的总隶属度函数表达式如附录E 式(E6)所示。 计算各Pareto 解集的总隶属度后,以总隶属度最大的解集为折中最优解,得到该最优解下的所有等价解。将所有等价解分别代入电网模型计算潮流分布,以网损最小的解为最优解。 为了验证本文所提模型和方法的有效性和合理性,在改进的IEEE 39 节点系统上进行仿真并引入真实电网数据作为分析对象。采用MATLAB R2018b 实现故障场景缩减、电网分区和多目标优化。 对于改进IEEE 39 节点系统,通过接入风电场、光伏系统及储能系统,构成含多类型可调资源并涉及不同概率特征的电网系统。其中,IEEE 39 节点系统详细参数见MATPOWER 工具包,本文在此基础上接入风电场、光伏系统及储能系统。系统结构见附录F 图F1,在节点3 和39 装设200 MW 的风电场,节点32 和33 装设200 MW 的光伏电站,节点35装设储能系统,储能系统额定容量为100 kW ⋅h,额定功率为100 kW,放电深度可达80%。 5.1.1 改进IEEE 39 节点系统的典型故障场景缩减分析 1)典型场景 新能源的波动性会对电网运行状态造成影响,从而产生大量的场景数据。根据真实电网全场景集中数据,本文采用场景缩减方法得到典型场景集。典型场景集数为4,典型场景集中新能源有功出力如附录F 图F2 所示。 2)故障场景聚类及典型故障场景选择合理性分析 为了验证t-SNE 降维方法的合理性,分别采用t-SNE 算法和主成分分析(principal component analysis,PCA)算法将故障场景的特征向量集降维到二维子空间,困惑度取30。t-SNE 算法和PCA 算法降维所得结果、降维可视化结果如附录F 图F3 所示。由图F3 可知,与PCA 算法相比,t-SNE 算法可以在低维空间内更直观地反映故障场景样本的特性,去除故障场景特征集的噪声。 对于降维后的故障场景特征向量集,通过层次聚类算法进行划分。聚类结果如附录F 图F4 所示。采用余弦距离和DVI 对各场景间的相似性和聚类方案进行评估,得到最佳聚类数为12。 通过电压稳定指标对故障场景进行评估,筛选出典型故障场景集。典型故障场景选择结果如附录F 图F5 所示,红叉处为典型故障场景中故障所发生的位置。场景集合如附录F 表F1 所示。 3)典型故障场景缩减方法效果分析 为验证本文所提典型故障场景缩减方法的有效性,设计了以下3 种方案进行对比分析: 方案1:采用全场景集合; 方案2:采用本文场景缩减法得到的场景集合; 方案3:采用文献[23]的故障筛选方法得到的场景集合。 在以上3 种方案下,针对改进IEEE 39 节点系统,采用非支配排序的遗传算法(non-dominated sorting genetic algorithm,NSGA)求解故障下区域无功储备多目标优化模型,优化结果如表1 所示。 表1 IEEE 39 节点系统典型故障场景缩减前后优化对比Table 1 Optimization comparison before and after reduction of typical failure scenarios in IEEE 39-bus system 由表1 中方案1 和2 的比较可知,方案1 和2 所得的故障下区域无功储备最小值优化结果相近,而方案2 中计算所需考虑的故障场景数目较少、优化所需时间较短且优化效率较高,验证了本文场景缩减方法的合理性,该方法可以在保证优化精度的同时,缩短优化所需的时间。由方案2 和3 的对比可知,方案2 中故障场景数目较少、优化所需时间较短且优化结果在精度上也要高于方案3 所得结果。因此,本文所提场景缩减方法在提高模型计算效率和精度方面均具有明显优势。 采用本文的典型故障场景缩减方法可以减少在故障下进行区域无功储备优化时需要考虑的故障场景数目。同时,在筛选过程中,由于仅需要考虑典型故障场景及与其电网电压稳定性紧密相关的有效无功源的作用,可以有效减少迭代所需要的时间,提高优化速度。相比之下,在筛选前,由于需要考虑所有故障场景下全部无功源及区域电网的无功储备,会影响优化时的计算速度、降低优化效率。 5.1.2 改进IEEE 39 节点系统的电网分区结果分析 为了验证基于改进D-K 聚类算法的电网分区方法的有效性,分别采用改进D-K 聚类算法、传统K-methods 算法、louvain 层次聚类算法进行电网分区,并采用模块度[24]指标对分区结果进行评价。考虑到改进D-K 聚类算法可以自动确定最佳聚类数而传统K-methods 算法需要手动确定聚类数,该算例中传统K-methods 算法同样选取最佳聚类数为o值。 改进D-K 聚类算法在聚类数为5 时所得分区方案的模块度最大,为0.617,具体分区方案如图2 所示。louvain 层次聚类算法所得分区方案的分区数为7,模块度为0.481;传统K-methods 算法所得分区方案的分区数为5,模块度为0.541。 图2 IEEE 39 节点系统分区方案Fig.2 Partition scheme of IEEE 39-bus system 在不同聚类算法得到的分区方案下,本文分区方法所得分区方案的模块度略高于基于传统Kmethods 聚类算法和louvain 层次聚类算法获得的分区方案,区域内电气距离联系更加紧密。同时,考虑到本文方法可以自动确定最佳聚类数。因此,本文基于D-K 聚类算法的电网分区方法相比其他分区方法更具优势。 5.1.3 改进IEEE 39 节点系统的故障下区域无功储备优化结果分析 为了验证所提优化算法的有效性,将所提多目标优化方法应用到改进IEEE 39 节点系统进行仿真分析。 1)不同目标下优化结果对比 本文分区方案中所得到的主导节点对于负荷节点的可控性较高,但对于无功源节点的可控性较低,因此,有必要把各分区中的主导节点可控性作为目标函数加入其中,将主导节点位置作为控制变量,使得主导节点处电压能够充分反映该区域内负荷及无功源所在节点的电压稳定性,从而更加准确地评估故障下区域无功储备。 采用NSGA-Ⅱ分别对单目标模型和多目标模型进行求解并对比不同目标下得到的最优解,优化结果如附录F 表F2 所示。由表F2 可知,单目标函数求得的目标值较大于多目标函数中对应的目标值,但其他目标值明显低于多目标函数中对应的值。这验证了构建多目标模型进行求解的合理性。 2)多目标优化算法对比 为衡量本文所用算法保持决策空间多样性的能力,在种群参数相同的情况下,分别采用NSGA、NSGA-Ⅱ和MMEA-NSGA-Ⅱ求解优化模型,3 种算法独立运行后所得的Pareto 最优解集如附录F 图F6 所 示。 采 用Pareto 解 集 近 似(Pareto set proximity,PSP)[25]对优化算法保持决策空间多样性的能力进行评估。该值越大,算法所得的等价解越多,保持决策空间多样性的能力越好。不同算法的PSP 指 标 如 表F3 所 示。 结合附录F 图F6 和表F3 可知,在相同因素下,MMEA-NSGA-Ⅱ搜索到的Pareto 最优前沿与真实的最优前沿更加相近。同时,加权指标和两阶段自适应群体更新策略提高了进化后期种群的多样性,避免陷入局部最优,提高了全局寻优能力。 采用4.2.4 节中的方法计算Pareto 最优解集中各解集的总隶属度,选取其中总隶属度最大的解集作为折中最优解。分别选取折中最优解下的等价解代入电网模型进行潮流计算,以网损最小的解为最优解。不同优化算法所得最优解结果如附录F 表F4 所示。由表F4 可知,本文的MMEA-NSGA-Ⅱ所得仿真结果的主导节点可控性和故障下区域无功储备均大于其他算法。 3)优化结果 改进IEEE 39 节点系统中,在考虑多类型资源无功调节能力的情况下,采用本文所提算法对优化模型进行求解。将优化前后故障下系统节点电压最低幅值进行对比,对比结果如图3 所示。 图3 优化前后故障下系统节点处电压最低幅值对比Fig.3 Comparison of the lowest voltage amplitude at system nodes before and after optimization 由图3 可知,无功优化前,节点15、20 的电压幅值均低于0.95 p.u.,其中,节点15 在N-1 故障下的最低电压幅值仅为0.936 p.u.,不满足安全运行约束。电压幅值原本较低的节点在优化后,其电压幅值均获得提高,保持在0.96 p.u.以上,电压质量获得改善,保证了系统电压安全。 4)多类型资源参与无功调节对比分析 为了验证多类型资源的无功调节能力能够有效增强电网电压稳定程度,在考虑多类型资源无功调节能力和不考虑多类型资源无功调节能力的情况下分别采用本文方法进行优化求解。不同情况下改进IEEE 39 节点系统的故障下区域无功储备最低值如附录F 图F7 所示。由图F7 可知,优化前电压裕度较差区域的故障下区域无功储备的最小值经过优化后有所增加,且在考虑多类型资源的无功储备后,故障下区域无功储备要高于不考虑多类型资源无功储备时对应的数值,有利于电网电压稳定裕度的提高。 采用真实电网数据对本文所提优化方法的有效性和合理性进行仿真验证。真实电网有65 个节点、71 条线路、33 个变压器,15 个电厂(其中2 个光伏电站、2 个风电站、1 个储能电站)。风光新能源电站的概率特征如5.1.1 节所示。真实电网结构示意图如附录F 图F8 所示,包含电压等级为110 kV 及以上的电网节点。 5.2.1 真实电网的典型故障场景缩减分析 为检验本文典型故障场景缩减方法的可行性,在真实电网模型中分别在4 个典型场景下进行N-1 预想故障扫描,得到的故障场景集有284 个。在典型场景集中,采用电压关联指标筛选出有效无功源后,根据故障场景集中信息构建故障场景的特征向量,采用t-SNE 算法对特征向量进行降维。结果如附录F 图F9 所示。由图F9 可知,t-SNE 算法提取出真实电网的故障场景特征向量的主要特征,实现了故障场景特征向量的可视化。 对于降维后的故障场景特征向量集,采用层次聚类算法对故障场景进行聚类。聚类结果如附录F图F10 所示。采用DVI 评估聚类效果,得到最佳聚类数为26,数量最多的4 个故障场景集的样本数量如表F5 所示。 采用电压稳定指标评估故障场景下电网稳定状态,筛选出典型故障场景集。典型故障场景在真实电网中的地理位置如附录F 图F11 所示,真实电网的典型故障场景集如表F6 所示。 为验证本文所提场景缩减方法对于真实电网的可行性,分别在故障场景筛选前后对真实电网中的故障下区域无功储备多目标优化模型进行求解,对比结果如附录F 表F7 所示。由表F7 可知,当采用典型故障场景缩减方法后,随着有效无功源和故障场景数的减少,优化所需的计算时间和迭代次数都有所下降,但优化结果相差极小。算例结果表明,所提场景缩减方法在保持较高计算精度的同时,能够有效提高求解速度。 5.2.2 真实电网的电网分区结果分析 采用改进D-K 聚类算法对真实电网模型进行分区,并采用模块度指标对分区结果进行评价。基于改进D-K 聚类算法的真实电网分区结果如附录F图F12 所示。改进D-K 聚类算法所得分区方案的模块度为0.451,说明电网划分出的社区结构强度较好,区域内电气距离联系紧密。 5.2.3 真实电网的故障下区域无功储备优化结果分析 将本文优化方法应用到真实电网模型进行仿真分析。 1)优化结果 在考虑多类型资源无功调节能力的情况下采用本文算法对多目标优化模型进行求解,对比优化前电压幅值较低节点的变化情况,优化前后该类节点的故障下电压幅值最小值对比如附录F 表F8 所示。由表F8 可知,优化后薄弱节点的故障下电压幅值最小值均有所增加,且能保持在0.96 p.u.以上,有效提高了故障下电网电压安全水平。 2)多类型资源参与无功调节前后的优化结果为比较多类型资源对于真实电网电压稳定程度的影响,将多类型资源作为无功源加入多目标优化模型的控制变量中,采用本文算法对优化模型进行求解。优化前后故障下的区域无功储备最低值见表2。 表2 优化前后故障区域无功储备最低值对比Table 2 Comparison of the lowest value of reactive power reserve in fault area before and after optimization 由表2 可知,原本故障下电压稳定裕度较低的区域经过优化后,对应的故障区域无功储备最小值均有所增加。且当多类型资源作为无功源参与优化后,电网各故障区域无功储备最小值得到有效增加。 由此可知,优化方案能够有效保证电网在故障下的电压稳定性,且当多类型资源参与无功调节后,优化方案显著提高了故障下电网电压安全水平,改善了故障下电网电压稳定裕度。 本文提出一种计及故障场景集的风光储混合系统区域无功储备多目标优化方法。针对复杂模型提出场景缩减和电网分区技术进行降维,采用改进算法求解多目标模型,主要特点如下: 1)提出一种考虑新能源波动性的典型故障场景缩减方法:构建一种电压关联指标,并基于关联指标通过故障场景划分策略获得典型故障场景集,实现对故障场景的降维,在模型优化精度基本不变的情况下有效减少了计算时间; 2)给出一种基于改进D-K 聚类算法的电网分区方法:通过构建一种区域主导节点控制空间,并引入改进D-K 聚类算法进行电网分区,进一步提升了分区质量,从空间维度实现对模型的降维; 3)提出一种基于典型故障场景的分区无功储备多目标优化方法;构建了一种新的故障下区域无功储备多目标优化模型,实现了故障下电网电压稳定裕度的提升; 4)给出一种MMEA-NSGA-Ⅱ对模型进行优化求解,进一步提高了多目标模型优化的收敛性和求解效率。 本文主要对输电网故障下的无功储备优化问题进行了研究,但并未涉及输配协同情况下的无功储备需求问题,这将是后续值得深入研究的问题。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
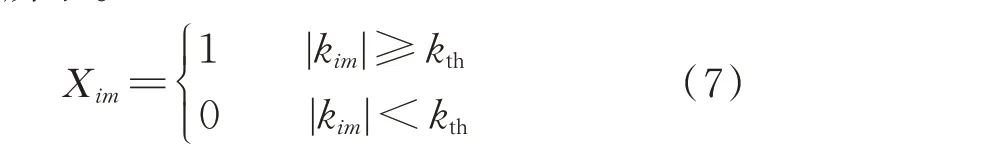
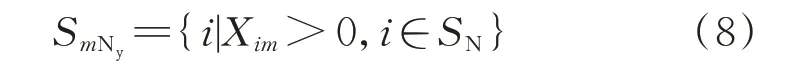
2.3 故障场景的聚类方法
2.4 典型故障场景的选择方法

3 基于改进聚类算法的电网分区
3.1 主导节点控制空间构建
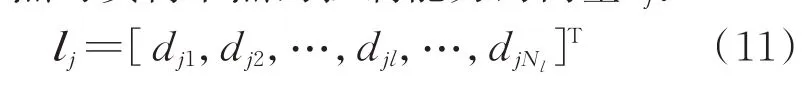
3.2 基于改进D-K 聚类算法的电网分区
4 基于典型故障场景的分区无功储备优化

4.1 多目标优化模型
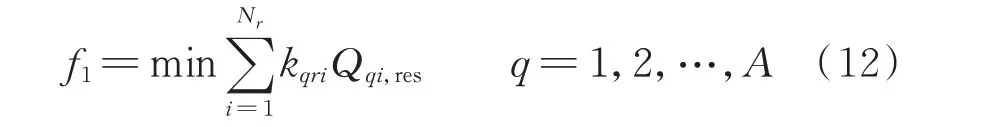
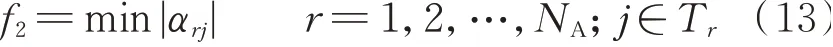
4.2 改进多模态多目标进化算法
5 算例分析
5.1 改进IEEE 39 节点系统

5.2 真实电网
6 结语
