考虑运营成本的电动公交车集群换电优化调度策略

2022-09-19蔡子龙束洪春单节杉

电力系统自动化 2022年17期

蔡子龙，束洪春，单节杉

（昆明理工大学电力工程学院,云南省昆明市 650500）

0 引言

经过多年的政策扶持和市场培育,以电动汽车为代表的新能源汽车产业取得了较大发展［1］。与此同时,为应对规模化电动汽车入网对电网造成的冲击,专家学者主要从以下几方面展开了研究:一是以减少充电成本和降低充电负荷波动为目标,研究对电动汽车进行有序充电［2-5］；二是研究电动汽车集群参与电网调峰［6］、调频［7-8］及电动汽车入网（vehicleto-grid,V2G）辅助服务［9-11］。此外,有学者还对电动汽车参与消纳和平抑光伏和风力发电进行了研究［12-14］。

电动公交车具有节能效果好、减排潜力大的优点,近年来在公交领域得到大力推广使用。一个大型公交车场的电动公交车集群集中无序充电会造成变压器和线路过载,增加网损,导致电压降落以及电网负荷波动增大［15-16］。同时,在分时电价机制下,无序充电的经济性较差,不利于电动公交车的经济运营。

换电模式具有换电时间短、换电标准易统一等优点［17-18］,适合具有较强运营规律的电动公交车使用。专家学者分别对电动公交车换电策略和运营调度策略进行研究。在换电策略方面,文献［19］从电网角度提出了一种基于换电规则优化、电池组与车辆匹配的充换电站日前优化-实时滚动修正两阶段充电优化策略。文献［20］考虑电动公交车运行规律和耗电特性,基于电池均衡使用和有利于充电的原则,建立了车辆日换电需求模型,以及以充电成本最小为首要优化目标的两阶段双目标优化充电模型。上述研究能从宏观层面给出电动公交车的充电负荷曲线和电池组的充换电计划,但无法具体得到每辆电动公交车一天的运营计划和每组动力电池的充换电计划,而这是电动公交车运营需要解决的核心问题。在运营调度策略方面,文献［21］以公交车辆总运营成本最小为目标,构建了纯电动公交车辆柔性调度优化模型。文献［22］以总固定成本和总运营成本之和为优化目标,建立了电动公交车区域行车计划编制模型。文献［23］建立了以最小化车辆数和空驶成本为优化目标的纯电动公交车调度模型。以上研究由于没有考虑电网分时电价机制,所建模型存在充电成本高和充电负荷波动大等问题。

在电网和交通网深度融合背景下,对电动公交车集群换电策略的研究需要兼顾电网和交通网等参与方的利益诉求［24-25］。文献［26］对单线路电动公交车的行车计划和充电策略问题进行了研究,但针对的是整车充电模式。换电模式下如何制定电动公交车集群的运营调度策略和换电策略,目前相关研究成果还较少,有待进一步深入研究。

本文的主要贡献是:在换电模式下,基于车次链思想对电动公交车集群换电策略和运营调度策略进行联合精细化建模。首先,以车次链总运营成本最低为优化目标,以覆盖所有车次任务、所使用的车辆数和换电电池数量为约束,建立了动力电池组与换电需求匹配模型。接着,以充电负荷波动最小为优化目标,建立电池组白天和夜间有序充电二次规划模型。此外,对电池组无序充电和应对突发情况的处理策略建立相应求解模型。通过以上模型求解出总运营成本最低的车次链集,确定与各车次链换电计划相匹配的动力电池组,以及各电池组白天、夜间有序充电策略。最后,以一个3 线路电动公交车集群换电策略和运营调度策略的制定为算例,对所建模型的有效性进行验证。

1 电池组与换电需求匹配模型

对电动公交车换电运营模式和换电策略的应用场景设置如下:

1）电动公交车的换电作业和电池组充电作业均在公交停车场进行；

2）电动公交车从车场出发执行完所有车次任务后均返回原车场；

3）车次链是满足时间接续关系的一组车次任务的集合,一个车次链仅由一辆电动公交车执行；

4）电动公交车的运营调度计划由多个车次链构成,且每个车次仅在车次链中出现一次；

5）每辆电动公交车配置一组动力电池。当电动公交车在执行车次链的某个车次任务后其动力电池电量不能继续执行下一个车次任务时,则需要从之前公交车卸载下来或者额外配置的动力电池组中选一个电池组换上,以完成后续车次任务；

6）卸载下的动力电池可通过充电作业满足后续的换电需求；

7）为减少换电次数和充电成本,规定每个车次链除最后一次换电外,其余次换电换上的都是满电量的电池组,最后一次换电换上的电池组电量仅需满足后续车次运行即可。

基于以上对应用场景的分析,以总运营成本最低为优化目标,建立动力电池组与各车次链换电需求的匹配模型。

1.1 换电参数设置

电池组与换电需求匹配模型较复杂,涉及的变量较多,将建立电池组与换电需求匹配模型之前需要确定的部分参数定义为换电参数。为确定换电参数,对模型中使用到的变量说明如下:1）电动公交车运营调度计划中车次链数目为Nc,参与调度的电池组数为Bc,备用电池组数为Bb(Bb=Bc-Nc)；2）调度最小时段长度设为Δt（单位为min）,将一天的时间分为T段,单次换电时间ΔT=δΔt,其中,δ为正整数,表示单次换电需要的基本时段数；3）将电动公交车运营调度计划分解成车次链并对车次链进行编号,编号为n（n=1,2,…,Nc）的车次链一共有Vn个车次任务需要执行；5）将执行第v(v=1,2,…,Vn)个车次的耗电量、执行前v个车次的总耗电量、第M次换电换下电池电量、换下电池时段、换上电池最低需求电量、换上电池最迟时段、车次链运行完毕后卸载的电池电量和卸载时段这几个换电参数分别设为en,v、En,v、El,M、aM、Eu,M、a͂M、Ew,n、Tw,n。这几个参数可由以下步骤求得。

步骤1:设置初始值M=0,n=1。

步骤2:取出编号为n的车次链,并将车次链n记为车次链n͂。

步骤3:若车次链n͂的耗电量满足式（1）,则需要换电,接着转步骤4 作进一步处理。

式中:Ef为电池组的满电电量；r为电池组的最低允许电量值与满电电量值的比值。若式（1）不成立,则车次链n͂没有换电需求,在其最后一个车次执行完毕后,可将其携带的电池卸载下来供换电使用,此时卸载下的电池电量Ew,n͂用式（2）进行计算,卸载电池时段记为Tw,n͂,然后转步骤6。

第M次换电的aM、a͂M分别记为车次v-1 结束时段的后一个时段和车次v开始时段的前一个时段。若执行完车次v-1 后,后续车次耗电量满足式（5）,则换电次数大于1。

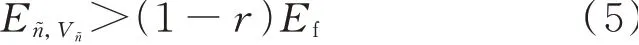
此时,第M次换上电池的最低需求电量Eu,M为:

步骤5:如果车次链n͂有换电需求,则将车次链n͂的第v个车次到第Vn͂个车次取出并组成一个子车次链n',并令n͂=n',转步骤3 处继续执行步骤3 至6。

步骤6:如果车次链n͂无换电需求,则结束车次链n͂的扫描工作。此时若n≠Nc,则取n=n+1,转步骤2 继续执行,否则结束整个车次链的扫描工作。

1.2 目标函数

当电动公交车执行完车次链最后一个车次任务后,可以提供1 组动力电池供换电使用,这样Nc辆电动公交车可提供Nc组可投入换电使用的电池组。而M次换电换下的M组电池也可作为电池组再投入使用,再加上Bb组备用电池,这样一共有D组电池可供换电使用,其中,D=Nc+M+Bb或D=Bc+M。至此,问题可总结为在d(d=1,2,…,D)组电池中选择M组,这M组电池经过充电（或不充电）用以满足M个换电需求,并使总运营成本最低。

设ΔE2=PΔt/60,表示关口计量处计量到的单位时段Δt的充电电量。第i个充电时间片段的充电成本cm,d,i为:

式中:ΔEm,d为最后一个充电时段实际充电电量。

式（12）—式（16）计算过程表明,由于以Δt为最小调度时间单位,充电时间片段先按向上取整的方式进行,最后一个时段充电到目标电量则立即停止充电作业,而不是充到整个时段结束,充电成本按关口计量处计量得到的充电量计算,以下类似情况均按上述方法处理。综上所述,这种情况下的Cm,d可表示为:

式中:Cmax为事先设定的一个比较大的数。

情况3:电池组d无须充电就能满足第m个换电需求。该情况下也分2 种情形,第1 种情形是E͂d≥Em,第2 种情形是电池组d为备用电池,因备用电池组一开始均为满电状态,可以匹配任何换电需求。这2 种情形下Cm,d可表示为:

式中:φm,d为0-1 变量,如果第m次换电由电池组d来承担,则φm,d取1,否则取0。

根据动力电池组与换电需求的匹配关系可确定每块动力电池与各车次链的对应关系,以及各电池组白天耗电量和充电电量,进而可求出其夜间需充电量。设第b(b=1,2,…,Bc)块电池的夜间充电需求为E'b,则最优车次链的夜间充电成本Cc2为:

1.3 约束条件

1）一个换电需求仅由一个电池组来承担,这一约束表示为:

2）一个电池组仅最多满足一个换电需求,这一约束表示为:

2 电池组充电优化模型

第1 章中电池组与换电需求匹配模型的主要作用是求出运营成本最低的电动公交车运营调度计划,确定与各车次链换电需求相匹配的动力电池组及各动力电池最优充电成本。由式（20）可求出与所有换电需求相匹配的动力电池的白天最优充电成本,但模型中并没有考虑总充电负荷波动情况,所得充电策略可能会拉大电网峰谷差。为此,本章以白天充电成本不大于式（20）所求出的充电成本为约束,建立以动力电池组充电负荷波动最小为优化目标的白天和夜间二次规划模型。

2.1 电池组白天充电优化模型

2.1.1 电池组白天充电优化模型的目标函数

对于与各换电需求相匹配的动力电池,如果该动力电池需要充电方能满足所匹配的换电需求,则按第1 章的方法枚举出各连续充电时间片段,并把所有充电时间片段按车次链的顺序进行排序。设有M'次换电需要对与之相匹配的动力电池进行充电,对于第m'(m'=1,2,…,M')个换电需求,通过式（13）、式（14）枚举出每个充电需求的充电时间片段长度和个数分别为T'm'和Lm',以总负荷波动最小为优化目标,电池组充电优化的二次规划模型定义为:

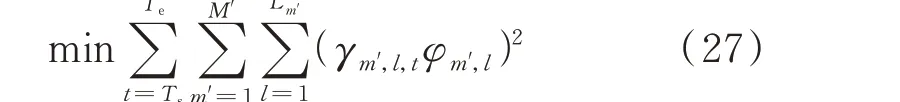
式中:γm',l,t为0-1 变量,表示与第m'个换电需求相匹配的动力电池的第l(l=1,2,…,Lm')个连续充电时间片段是否包括时段t,如果包括则取为1,否则取0；φm',l为0-1 变量,表示最终解中与第m'个换电需求相匹配的动力电池的第l个充电时间片段是否被选中,若被选中则取1,否则取0；Ts、Te分别为白天充电开始时段和结束时段。

2.1.2 电池组白天充电优化模型的约束条件

1）与第m'个换电需求相匹配的充电时间片段只有一个,这一约束定义为:

2）设与第m'个换电需求相匹配的动力电池的第l个充电时间片段的充电成本为fm',l,则第m'个换电需求的充电成本为:

因白天充电电价比夜间高,而车次链的总耗电量不变,当白天充电成本最低时,总充电成本也最低,因此充电成本约束表示为:

2.2 电池组夜间充电优化模型

2.2.1 电池组夜间充电优化模型的目标函数

编号为b(b=1,2,…,Bc)的电池组的夜间充电持续时间片段长度为:

式中:ψz,t为0-1 变量,表示第z个连续充电时间片段是否包括t时段,若包含则取1,否则取0；γz为0-1 变量,表示充电时间片段z是否被选中,若被选中则取1,否则取0；Ta、Td分别为夜间充电的开始和结束时间。

2.2.2 电池组夜间充电优化模型的约束条件

设编号为b的电池组的连续充电时间片段在总时间片段中的开始编号为ns,b,结束编号为ne,b,电池组b在夜间仅进行一次充电,这一约束表示为:

2.3 电池组无序充电模型

文献［26］针对整车充电模式下无序充电策略进行研究,在换电模式下需要重新制定各动力电池组的无序充电策略。对于执行各最优运营调度计划的各电动公交车,在无序充电模式下,不考虑电网的分时电价,电动公交车进站后即进行充电作业。对

2.4 运营中异常情况处理策略

在电动公交车的最优运营调度计划及其换电策略制定完毕后,在运营过程中每辆电动公交车只需按车次链顺序执行所有车次任务和换电任务,电池组按充电计划完成各自的充电任务,则电动公交车集群一天的运营可以顺利完成。但电动公交车运营过程中的单位行驶里程的能耗值与所处季节、道路拥堵情况、车辆运行速度、车辆质量和载客人数等密切相关,并不是一个固定值。本文对电动公交车单位行驶里程的能耗值变化分2 种情况进行处理:1）对于日前调度,因电动公交车单位行驶里程的能耗值是指车辆型号、载客人数、季节和道路拥堵情况确定的情况下,车辆长期载客运营的平均能耗值。当季节变化或拥堵情况变化时,只需将新的单位行驶里程能耗值代入模型重新进行优化计算,生成新的车次链及各车次链换电计划即可。2）对于实时调度,当天气、路况拥堵情况发生较大变化以及变压器容量限制等特殊异常情况发生时,需对原有充电计划进行调整。文献［26］的异常情况处理策略针对的是整车快充模式,在换电模式下需要重新制定异常情况处理策略。由于电池组的充电计划是在总充电负荷波动最小的基础上生成的,当异常情况发生时,为继续完成原有车次链,需要对执行发生异常情况的车次链的动力电池组的原有充电计划进行调整。考虑一种较复杂的情况,当异常情况发生时,与第m个换电需求相匹配的第d个电池组的开始充电时段向后延迟Δtd时段,可充电开始时间为:

若计算t'd至q'm之间所有充电时段均充电的情况下电池电量不能达到Êm,则可从其他已经完成车次链任务并且后续不再使用的电池组中选择一块电池,判断其携带电量加上最大相应可充电时长的充电量后是否满足第m个换电需求。如果满足,则计算充电成本,并从所有满足第m个换电需求的电池组中选择一组充电成本最小的电池组,并按式（41）—式（45）对充电计划进行优化,否则需启用额外的备用电池组以完成后续车次的运营。

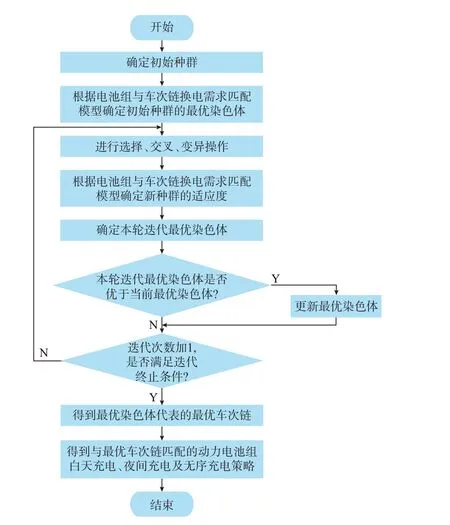
3 模型求解算法

遗传算法（genetic algorithm,GA）是美国Holland 教授于1975 年提出的一种借鉴生物界适者生存、优胜劣汰的生物遗传机制发展起来的随机优化搜索方法,广泛应用于函数寻优、旅行商等问题的求解［27］。将遗传算法应用于求解公交运营调度计划编制问题,目前已有较多的研究成果［23-25］。本文根据换电模式下电池组与换电需求匹配模型的特点,使用改进的遗传算法求解该模型,对染色体编码方式、适应度函数、选择、交叉、变异等操作进行了设计。

3.1 染色体编码方式

常用的遗传算法的染色体编码方式有二进制编码方式和十进制编码方式,并不适用于求解本文提出的动力电池组与换电需求匹配模型。根据问题的特点,本文提出以自然数编码方式作为染色体编码方式,以车次链为基本单元,车次链之间用0 分隔以区分不同的车次链,将覆盖所有车次任务的车次链组合在一起构成一个染色体。考虑一共有10 个车次任务的染色体编码方案,该染色体由1-4-7-10、2-5-8、3-6-9 这3 个车次链构成,其编码方式为:1-4-7-10-0-2-5-8-0-3-6-9。

3.2 适应度函数

适应度函数是用于评价种群中个体优劣的指标。在换电电池数量确定的情况下,由式（23）计算得到的目标函数值越小,表示该个体的适应度越高,遗传到下一代的概率越大,反之则遗传到下一代的概率越小。因此,用式（23）计算结果的倒数作为遗传算法的适应度函数,记为:

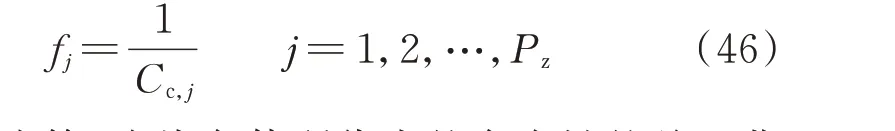
式中:Cc,j为第j个染色体所代表的车次链的总运营成本；Pz为种群规模。

3.3 选择算子

选择操作的作用是从种群中按优胜劣汰的原则选择个体遗传到下一代。选择操作次数设为种群规模Pz。根据式（46）计算得到各个体的适应度,采用轮盘赌选择算子和精英保留策略确定遗传到下一代的个体。设代沟为G,表示种群中会有Pz(1-G)个精英个体直接遗传到下一代。第j个个体被选中的概率由式（47）决定。

选择操作的策略如下:

1）根据式（46）选择适应度最高的Pz(1-G)个精英个体直接遗传到下一代。

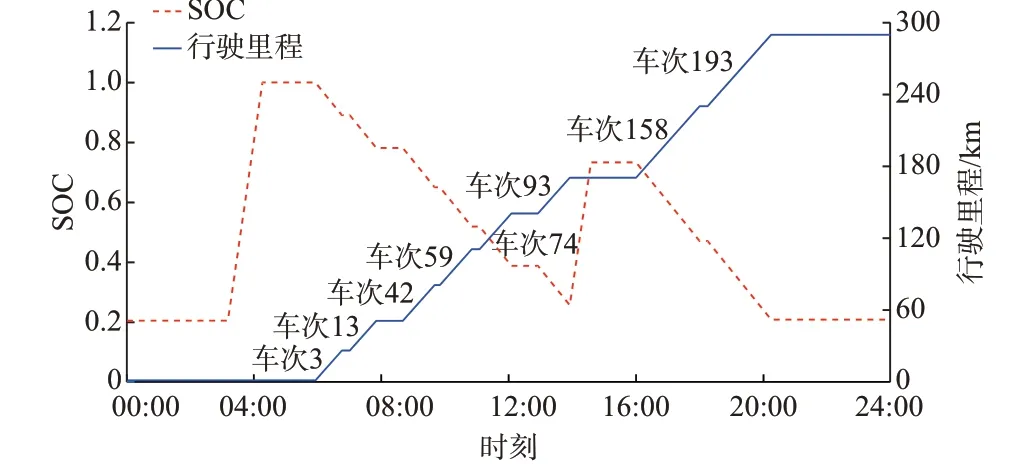
2）将种群中各个体按pj从小到大的顺序排列。对于第j(j=1,2,…,NG)次选择操作,随机产生一个［0,1］之间均匀分布的随机数,设为ps。按轮盘赌方式扫描种群中依次排列的多个体的pj,如果该随机数满足pj-1

3）继续下一轮轮盘赌,直到循环次数j达到NG时为止,这样就产生了和种群规模同样多的个体遗传到下一代。

3.4 交叉算子

通过交叉操作可以生成新的染色体个体,以改善种群质量。由于染色体采用自然数编码,需要设计出专门的交叉算子。设交叉操作次数和交叉概率分别为Pz和pc。交叉算子操作如下:

1）确定进行交叉操作的一对染色体。对于第j(j=1,2,…,Pz)次交叉操作,随机产生一个［0,1］之间均匀分布的随机数rc,若rc>pc则不进行本次交叉操作,否则随机生成2 个［0,1］之间的随机数,将2 个随机数乘以种群规模并向上取整,得到2 个整数,这2 个整数表示进行交叉的2 个染色体个体的编号。例如,假设选择到2 个由10 个车次组成的染色体进行交叉操作,这2 个染色体的编码如下:

染色体1:1-4-7-10-0-2-5-8-0-3-6-9。

染色体2:1-5-7-10-0-2-4-6-9-0-3-8。

2）确定进行交叉操作的车次链。对上述产生的2 个交叉个体,随机生成2 个［0,1］之间的随机数,用2 个随机数乘以各染色体所含有的车次链个数,得到2 个进行交叉操作的车次链cross1 和cross2。在上例中,假设分别选中2 个染色体中的第3 和第1 个车次链进行交叉操作,选中的2 个车次链为:

cross1:3-6-9。

cross2:1-5-7-10。

3）将染色体1 中的车次链cross1 删除,同时,将既在染色体1 中又在cross2 中的车次从染色体1 中删除。对染色体2 按相同方法进行处理,将染色体2中的车次链cross2 删除,同时,将既在染色体2 中又在cross1 中的车次从染色体2 中删除。上例按此操作,染色体1 和2 分别变为:

染色体1a:4-0-2-8。染色体2a:2-4-0-8。

4）将cross2 作为首车次链插入染色体1a中,并将在cross1 而不在染色体1a中的车次插入染色体1中。车次插入车次链的规则为:首先,车次插入时前后车次要满足时间接续关系,同时,若插入车次后车次链新增换电需求,则还应满足换电所需时间要求；其次,插入车次时从左到右对染色体中各车次链进行逐一扫描,当发现车次能插入到某车次链时即进行插入操作,插入后即终止后续车次链的扫描工作；如果对所有车次链扫描后仍无法插入,则新建一个以该车次为首车次的车次链。本文中车次插入车次链时均按上述规则进行,并且假设车次插入时均满足时间接续关系。按上述规则上例中染色体1a经过这一步操作得到的新染色体如下:

染色体1b:1-3-5-7-10-0-4-6-9-0-2-8。

5）对染色体2a按第4）步的方法作相同处理,经处理后得到的新染色体如下:

染色体2b:1-3-6-9-0-2-4-7-10-0-5-8。

6）最终得到的染色体1b和2b就是染色体1、2 交叉的结果,将2 个染色体保留到下一代群体中。

7）若交叉次数没达到Pz次,则转第1）步,否则结束本轮交叉操作。

3.5 变异算子

变异的过程就是基因重组的过程,通过变异能改善染色体的适应度。设变异操作次数和变异概率分别为Pz和pm。变异算子操作如下:

1）对于第j(j=1,2,…,Pz)次变异操作,随机产生一个［0,1］之间均匀分布的随机数rm,若rm>pm则不进行本次变异操作,否则将该随机数乘以种群规模并向上取整,得到进行变异操作的染色体个体。例如,假设一个包含10 个车次,由3 个车次链组成的染色体被选中进行变异操作,该染色体的编码为:

染色体3:1-3-8-0-2-4-6-9-0-5-7-10。

2）考虑到电动公交车的运营调度计划由车次链构成,本文将变异操作的变异位定义为染色体中某个选中的车次链,在进行变异操作时首先将该车次链从染色体中删除,类似于将二进制编码方式的染色体的变异位从1 变到0。接着将所删除车次链的各车次按前述的车次插入规则插入到染色体中,从而保证染色体覆盖所有的车次任务。具体操作时,首先,随机产生一个［0,1］之间均匀分布的随机数,将该随机数乘以染色体中所含的车次链个数并向上取整,得到进行变异操作的车次链。然后,将该车次链从染色体中删除。对上述染色体3,假设进行变异操作的是第2 个车次链2-4-6-9,将第2 个删除后得到新的染色体3a为:

染色体3a:1-3-8-0-5-7-10。

3）将第2）步中删除的车次链的各车次重新插入到染色体中。例如对染色体3a,将车次2、4、6、9各车次重新插入后得到的新染色体3b为:

染色体3b:1-3-8-0-2-5-7-10-0-4-6-9。

4）将第3）步得到的染色体保留到下一代种群中。上例中将染色体3b替换染色体3 并保留到下一代种群中。

5）若变异次数没达到Pz次,则转第1）步,否则结束本轮变异操作。

3.6 初始解的生成

初始解即初始种群,是按染色体编码方式生成的包含所有车次任务的所有初始染色体的集合,质量良好的初始解可以加快求解速度。为提高初始解的质量,本文采用文献［23］提出的用于解决经典装箱问题的贪婪算法生成初始解,初始解的生成主要包含以下步骤:

1）生成含有所有车次任务的集合Φ,从Φ中任取一个车次并生成以该车次为首车次的车次链,并将该车次从Φ中删除,转第3）步；

2）从Φ中的剩余车次中任取一个车次,生成以该车次为首车次的车次链,并将该车次从Φ中删除；

3）从Φ的剩余车次中选择出与上述车次满足时间接续关系的所有车次,并组成一个车次集合ψ。为提高初始解的质量,将ψ中的车次按车次出发时间进行升序排序,根据ψ中车次的规模确定一个数ε（ε可根据车次集合中车次的个数动态确定）,并在该升序排列的车次集合ψ的前ε个车次中随机选中一个车次,将该选中车次插入到上述车次之后作为后续车次,同时将该选中车次从Φ中删除。重复第3）步,直到剩余车次均无法插入上述车次链时为止,这样就生成了一个车次链；

4）重复上述第2）步和第3）步,直到所有车次都插入到相应车次链后,即完成一个初始解的生成。

当按上述方法生成的初始解的个数达到规定的初始种群规模时,就完成了初始解的生成。

4 算例分析

4.1 仿真场景和参数设定

系统运行流程图如图1 所示。电动公交车选用型号为XMQ6106AGBEVL25 的纯电动城市客车,该车长10.5 m,最高时速为69 km/h,车辆加电池成本为120 万元,设置6 年的报废期,忽略资金的时间价值,车辆日均使用成本cg=548 元。遗传算法参数取值情况如下:种群规模Pz为100,迭代次数为100,交叉概率pc为0.7,变异概率pm为0.1,代沟G为0.8。其余参数设置如下:T=288,Δt=5 min,Ts=1,Te=65,Ta=66,Td=288,δ=1,r=0.2,P=200 kW,η=0.9,Cmax=1 000元。参与调度的动力电池组数Bc为38。电动公交车场共有3 条线路的206 个车次任务需要执行,车次任务时刻表、公交线路参数和分时电价如附录A 表A1—表A3所示。

图1 系统运行流程图Fig.1 Flow chart of system operation

4.2 运行结果及分析

根据图1 所示的系统运行流程图,采用MATLAB 2016 编写程序对所建模型进行优化计算。对于遗传算法种群中的每个个体的最优白天充电成本和最优运营成本均通过MATLAB 2016 调用Gurobi 8.0.1 软件进行优化计算,优化过程如附录A 图A1 所示。经优化计算后得到的最优车次链及其换电情况如表A4 所示。从表A4 中可以看出,完成206 个车次任务共需要35 辆电动公交车,一共有22 次换电作业。总运营成本的目标函数值的迭代过程如图2 所示。

图2 总运营成本曲线Fig.2 Curve of total operation cost

图2 所示的总运营成本曲线是在处理器为主频2.5 GHz Intel Core i5-4200 的个人计算机的MATLAB 环境下编程并调用Gurobi8.0.1 优化软件进行求解得到,问题的车次规模为206 个车次,属于大规模0/1 整数规划问题,对每一个染色体均需要做多次优化,完成全部求解任务需要27 663 s（约为6.78 h）。在季节和拥堵情况确定的情况下,电动公交车的百公里耗电量将基本保持不变,可根据季节和拥堵状况确定最优车次链及其换电计划,因此,模型使用的频次并不高。考虑到问题的规模、模型的复杂度和模型的使用频次,模型的求解时间是可以接受的。从图2 中可以看出,由于初始解采用了贪婪算法,初始解的质量已经处于较高水平。随着迭代次数的增加,总运营成本呈下降趋势,当迭代次数超过65 次时,最优总运营成本已经基本保持不变,运行结果显示了本文所提的遗传优化算法的有效性。

设35 辆电动公交车各自携带的动力电池组编号为1 至35,3 组备用电池的编号为36 至38。电池组及与其匹配的车次链和满足的换电需求如附录A表A5 所示。运行结果显示最优染色体代表的车次链的总运行成本为22 733 元,白天充电成本为957 元,夜间充电成本为2 596 元。

将最优染色体所代表的车次链的换电需求与动力电池组的匹配关系,以及最优染色体所代表的车次链的白天充电成本代入2.1 节的电池组白天充电优化模型和2.2 节电池组夜间充电优化模型中,使用MATLAB 2016 编写程序并调用Gurobi 8.0.1 优化软件,按附录A 图A2 所示的流程对所建模型进行求解,经优化计算得到最优车次链总充电负荷曲线如图3 所示,各电池组充电情况如表A6 所示。

图3 充电负荷曲线Fig.3 Curve of charging load

从图3 所示的总充电负荷中可以看出,电池组绝大多数充电行为都在分时电价的平时段进行,在分时电价峰时段充电较少,并且总体充电负荷波动较小。充电行为主要在夜间分时电价谷时段进行,且夜间谷时段的充电负荷波动较小,但需要投入较多的充电桩,高峰投入的充电桩个数为9 个。由于采用2.1 节提出的以负荷波动最小为优化目标的优化策略,白天充电行为主要发生在分时电价的平时段,同时充电负荷波动较小,峰时段仅需投入2 个充电桩。

以电池组1 至4 为例,电池组的充电功率示意图如附录A 图A3 所示。从图A3 可以看出,各电池组的充电主要在夜间分时电价谷时段和白天分时电价的平时段进行。

对于车次链,可以画出车次链的各车次行驶里程和执行车次链的各电池组荷电状态（SOC）变化示意图。以车次链2 为例,其执行各车次任务时行驶里程与执行该车次任务的电池组SOC 变化过程如图4 所示。图4 中,车次链2 的车次任务3、13、42、59、74、93 先由电池组2 执行,耗电量为187 kW∙h,剩余电量为63 kW∙h,SOC 降至0.252。后续车次任务110、141、175、192、201 由电池组28 执行,其在执行车次链28 的前6 个车次后耗电量为176 kW∙h,剩余电量74 kW·h,后在13:16—13:54之间充电119 kW∙h至193 kW∙h,转至执行车次链2 的后5 个车次,耗电量为143 kW∙h,剩余电量为50 kW∙h,SOC 降至0.2,不小于规定的动力电池SOC 最低值。车次链2 的总行驶里程为300 km。

图4 执行车次链2 的电池组SOC 与行驶里程变化关系示意图Fig.4 Schematic diagram of relationship between SOC of battery pack and driving mileage change of vehicle chain 2

对于电池组,可以画出其执行各车次任务时行驶里程与SOC 变化的关系示意图。以电池组2 为例,其SOC 变化示意图如图5 所示。在图5 中,电池组2 首先服务车次链2,完成车次任务3、13、42、59、74 和93 后耗电量为187 kW·h,剩余电量为63 kW·h,SOC 降至0.252,在13:56—14:29 间充电119 kW·h,剩余电量为182 kW·h,SOC 升至0.728,最后服务于车次链31,完成车次任务158、193 后耗电量为132 kW·h,剩余电量为50 kW·h,SOC 降至0.2,不低于规定的动力电池最低SOC 允许值0.2,最后在夜间03:10—04:20 之间补充电量200 kW ∙h,SOC提升至1。电池组2 的行驶里程为290 km。

图5 电池组2 的SOC 与行驶里程变化关系示意图Fig.5 Schematic diagram of relationship between SOC of battery pack 2 and driving mileage change

改变能投入运营的动力电池组数量,代入本文所提模型中,可求解出不同动力电池组数下的车次链数目、车次链白天充电成本、夜间充电成本、需要的车辆数和总运营成本等参数,如表1 所示。

表1 系统运营成本与电池组数量关系Table 1 Relationship between system operation cost and battery pack quantity

不同电池组组数下系统白天总充电功率示意图如图6 所示。

图6 白天充电功率随电池组数的变化示意图Fig.6 Schematic diagram of daytime charging power changing with number of battery pack

从表1 和图6 可以看出,4 种情况下投入的电动公交车数量均为35 辆。由于完成所有车次任务的总耗电量均相等,随着投入运营的动力电池组数量的增加,白天充电成本和总运营成本呈现下降趋势,夜间充电成本呈现增加趋势。这是因为多投入的动力电池组可以降低电价高峰时段的充电需求,从而降低白天充电成本和充电电量。在总耗电量一致的情况下,相应增加了夜间充电需求。从图6 中还可以看出,当投入运营的动力电池组数量较少时,白天充电的电网峰谷差较大,而当动力电池组数量增加时电网峰谷差相应减小。

4.3 无序充电案例分析

根据2.3 节提出的无序充电策略,对车次链2 的无序充电情况进行分析。当电池组28 完成车次链28 的前6 个车次任务时耗电量为176 kW∙h,剩余电量为74 kW∙h,后转至执行车次链2 的后5 个车次任务,耗电量为143 kW∙h,将上述参数代入2.3 节的模型中,根据式（36）可得最大能充电量为176 kW∙h,根据式（37）可得最大可充电量时间为1 h 35 min,可充电量为194 kW∙h,根据式（38）可得实际充电电量为176 kW∙h,充电时间为13:01—13:59,比有序充电模型白天多充电57 kW∙h,多产生充电成本43元,充电的经济性较差。

4.4 异常情况处理案例分析

按2.4 节给出的异常情况处理策略对发生异常情况的车次链进行处理。以车次链2 为例,车次链2先由电池组2 执行,执行完车次任务3-13-42-59-74-93 后,其后续车次任务110-141-175-192-201 由电池组28 执行。而电池组28 首先执行第28 个车次链,正常情况下完成车次任务1-15-30-54-69-85 的耗电量为176 kW∙h,时间为13:00。但由于发生了突发情况,耗电量实际为190 kW∙h,剩余电量为60 kW∙h,到站时间推迟至13:10。经计算,后续车次任务的总耗电量为143 kW·h,第1 个车次110 的出发时间为14:36,可得到需充电量为83 kW∙h,充电桩功率和效率仍分别取200 kW∙h 和0.9。充电时间在13:11—14:35 之间选择。代入式（41）—式（45）进行优化计算,得到优化后的时间段为13:21—13:50,实际补给能量为83 kW∙h,充电时间约为27.6 min,即到13:47:36 停止充电。由于13:11—14:35 处于电价平时段,因此这样的解会有多个,可根据具体情况加以选择。上述计算过程表明异常情况的处理仅影响本车次链的充电计划,而不影响其他车次链的充电计划和运营计划的执行。