算法精度评估中的风险观点
2022-09-19薛禹胜黄天罡谢云云
吕 睿,薛禹胜,郁 琛,黄天罡,谢云云
(1. 南京理工大学自动化学院,江苏省南京市 210094;2. 南瑞集团有限公司(国网电力科学研究院有限公司),江苏省南京市 211106;3. 智能电网保护和运行控制国家重点实验室,江苏省南京市 211106)
0 引言
电力系统规划、运行调度、安全控制、市场运营与能源转型等问题,不仅涉及发电、输电、配电等物理环节,还可能与电价建模或行为建模有关[1-3],它们都需要算法支持[4]。不论是离散型的定性分析还是连续型的定量分析,除了要在计算精度和速度之间折中外,还需要了解其分析结果的精度及强壮性,这就需要建立合理的误差评估指标。恰当的误差评估不仅可用以评估算法的准确性,而且也可帮助算法选取最优参数值。
通常,误差以数学模型的仿真结果与现场实测的结果之差来反映,并且可根据误差评估指标的敏感性分析来估计误差来源或评估模型的适用性与强壮性。有别于纯数学的观点,在工程问题中,误差绝对值相同,但误差符号不同的结果,往往有不同的物理含义及经济影响。这就要求在算法误差评估指标中给予反映,而在不必区分误差符号的场合,只须将权值设为相同即可。
对于风电功率的预测[5-6],正误差反映风电水平被高估的情况,而负误差则对应于风电水平被低估的情况。正误差导致正常运行计划中的其他一次能源的发电水平偏低,一方面,降低了正常运行下的供电充裕性;另一方面,与风电不确定性正相关的灵活发电备用需求却会被高估,从而增加了备用成本。这2 种影响虽然在宏观上有一定的对消趋势,但由于因果关系不同,优化的整体效果将会下降。反之,风电功率预测的负误差则以相反的规律来降低运行的可靠性及经济性。
然而,负荷预测[7]的正误差会使发电计划和备用计划同时趋于保守,不再存在两者对消的趋势,故与风电功率预测误差对符号敏感性的关系存在定性的不同。这样的情况广泛出现在风速预测[8-10]、状态估计[11]等许多领域中。因此,误差评估指标应该能反映相关样本算例的误差符号的影响。不失一般性,下面以电力系统暂态功角稳定分析问题为例来讨论。
电力系统暂态功角稳定分析离不开合适的数学模型和数值积分技术,一般的分析方法在获得足够时长的时间响应曲线后,凭经验定性地判断具体算例是否稳定。需要时,可以通过反复试探来获得参数的临界值(例如临界故障清除时间),并取为标准值来评估其他算法的误差。集成扩展等面积准则(integrating extended equal area criterion,IEEAC)是目前唯一可以从上述受扰轨迹中直接提取轨迹稳定裕度的量化分析方法,可以揭示电力系统动态过程中的各种涌现现象,包括分岔与混沌,并被广泛应用于国内外电力工程。此外,可以通过灵敏度分析技术直接获得参数的临界值,故计算量很小[12],可被用做在线分析工具。IEEAC 的误差来自2 个部分:1)积分求取受扰轨迹时产生的误差;2)积分轨迹中提取稳定裕度的误差。由于后一部分是严格的初等代数运算,并且其映射步长采用了与数值积分相同的步长,因此,IEEAC 的总误差与它所依据的数值积分技术处于同一水平[12]。
为了应对系统规模和模型复杂性的增加对计算量的新挑战,文献[13]在先前关于分类器(case filtering,CF)大量研究[14-18]的基础上进一步将定性多档分类、准定量分析与IEEAC 相结合,构成7 分类输出的分类器(7-output CF,CF-7)。它先采用2 分类输出的分类器(2-output CF,CF-2)将大量待分析的算例粗筛为“肯定稳定”与“可能不稳定”2 个子集;再将前一子集内的算例,细分为{高度稳定,中度稳定,低度稳定};将后一子集细分为{轻度失稳,中度失稳,严重失稳,不能确定}。这样,精确而费时的IEEAC 定量算法就可以只被用于评估那些被分到“不能确定”子集的算例,而其他的大量算例则直接被多输出分类器分到稳定裕度的各个离散区间,从而显著提高了效率和强壮性。
当然,其前提是要确保在风险性误分类率(将实际稳定性等级较低的算例划分到稳定性等级较高子集的占比)为零值的同时,尽量减少降效性误分类率(将实际稳定性等级较高的算例划分到稳定性等级较低子集的占比),从而使更多的算例能够采用较大的积分步长和映射步长,进一步减少计算量[18]。为此,除了要更好地协调数据驱动技术的快速性与因果分析技术的强壮性,还要通过优化分类器的各个分类阈值,来适度容忍降效性误分类率,以保证风险性误分类率为零值。这就要求在设定分类阈值时,要区别对待算例近似算法对应的正负误差值。
电力系统分析算法的研究采用了各种误差评估指标,包括平均误差(mean error,ME);基于绝对误差概念的平均绝对误差(mean absolute error,MAE)[19]、平 均 绝 对 百 分 比 误 差(mean absolute percentage error,MAPE)[20]、最 大 绝 对 误 差(maximum absolute error)[21]、均 方 根 误 差(root mean square error,RMSE)[22-23];基于相对误差概念的平均相对误差(mean relative error,MRE)[22]、最大相对误差(maximum relative error)[24]、均方百分比 误 差(mean square percent error,MSPE)[25]和MRE 的 衍 生 指 标[26];基 于 偏 差 概 念 的 方 差(variance)[21]、标准差(standard deviation)[27];归一化指 标,如 NMAE(normalized MAE)、NRMSE(normalized RMSE)[6]。此外,统计学中的众数、中位数、偏度、峰度也被用来反映算法误差的个别特征。
但是对于许多具体问题,这些指标和特征都不能正确反映误差符号在物理内涵上的不同,也不能反映误差影响的非线性。即使同时采用其中的多个指标[28],也不可能避开误差评估指标中的上述本质缺陷。
为了能在考虑安全约束的控制优化问题中,协同处理安全性及经济性,文献[29]提出了风险代价的概念,从而将安全约束条件转换为与目标函数中建设费用、运行费用并列的风险费用。风险代价被定义为2 项内容之乘积,其一是随机事件发生的概率,其二是为保持系统可靠运行而付出的控制代价。以全部随机事件对应的风险代价之和来评估各候选方案的安全成本,并加入选优的目标函数,解决了如何处置小概率高风险事件的难题。
风险代价中关于控制代价的一项反映了事件的具体影响,包括定性的后果及定量的后果,而对于误差评估问题,则对应为误差的符号及大小。这就为误差评估指标提供了全新的设计思路,不但能区分误差后果的符号敏感性和强非线性,并且能合理处置小概率大误差算例的影响。根据此概念,文献[5]考虑了误差符号及非线性的影响,设计了用于评估风电预测误差的指标,并协同处理了风电预测误差对系统可靠性及经济性的影响。
本文归纳了误差评估指标应满足的要求;回顾了传统的误差评估指标的局限,基于上述风险观点设计了电力系统算法的误差风险指标(error risk index,ERI),并通过分析该指标的特性及计算方法表明其可行性。最后,针对暂态功角稳定分析中算例筛选分类器的阈值优化问题,通过实例比较了按照不同的误差指标来优化CF-7 分类阈值的效果,验证了误差风险指标的合理性。
1 算法误差评估指标的要求与现状
1.1 算法误差评估指标的要求
在算法精度的比较与提高中,误差评估指标起着重要作用。基于文献[12]对定量型指标提出的基本要求,电力系统算法误差的评估指标应满足的条件包括:1)唯一性,即对于确定的误差情形有且仅有1 个指标值;2)充要性,即严格反映误差的符号,零值对应于与标准值相同;3)单调性,即指标值应与客观的误差水平的变化方向保持一致,可按指标值对算法精度排序;4)可观性,即指标评估体系能反映算法的任何改变对精度的影响;5)可控性,即按照指标值的灵敏度分析可以指导算法精度的提高;6)连续性和光滑性(或可微性),即误差评估指标随参数连续光滑地变化;7)可反映误差绝对值对实际电力工程影响的非线性;8)反映误差符号对实际电力工程的不同影响;9)可将上述影响直接反映为机会成本或风险成本;10)不但适用于电力系统的静态分析,也适用于电力系统的动态分析及演化过程分析。
1.2 传统评估指标的局限性
大多数传统指标能满足唯一性、充要性、单调性、可观可控性、连续光滑性等基本要求,但却难以反映工程实际对误差影响的非线性、符号敏感性,因此也无法全面反映工程算法的性能。文献[28]以MAE 和RMSE 作为长期监测系统整体误差的指标;以误差的频度直方图来估计不同误差水平下预测结果的可信度,并以其对零点的集中程度作为性能评估的依据之一;根据影响因子分布来判断主要误差源;提出相关系数来评估实测序列与预测序列的相似度;以功率波动幅度及变化率的概率分布来评估峰/谷值的预报质量。虽然采用多个指标,但并未提出合理的综合方法,因此,很可能兼具各种指标的缺陷。如果不能将误差转换为风险成本,在电力系统优化算法,特别是带有不等式约束的分析或控制问题中,都存在较大的局限性。
1.2.1 物理内涵的扭曲
将所有样本的误差原始值求和后再取均值,会因为正负误差的对消而扭曲了实际的误差水平。文献[30]先将各个预测样本分类为偏冒进和偏保守2 个子集,再分别求取其ME,以克服均值方式的缺陷。由于未能用统一的指标来反映全部样本的预测质量,故难以得到实际应用。绝大多数误差评估指标都采用了另外一条技术路线,即对样本误差采取绝对值或平方化的方式(见附录A 表A1)。
这些指标在避免正负误差对消的同时,却掩盖了误差符号对许多工程问题的物理与经济影响的不同。文献[5]阐明了风电预测算法的误差符号及非线性对电力系统可靠性及经济性的影响。预测误差为正(预测值大于实测值)使常规机组发电容量安排偏少,从而与风电预测值正相关的备用灵活发电容量则要求偏多。这2 种影响虽然有相互补偿的一面,但由于考虑的措施及不确定性均不相同,并不能相互抵消,从而影响优化结果。预测误差为负时的情况则相反,但同样会影响优化结果偏离实际的最优值。
1.2.2 误差指标值与其实际影响的非线性
在实际工程中,误差与其实际影响之间的关系既可能相当接近线性,也可能含极强的非线性。例如在紧急控制决策算法中,若误差引起过控,则通常仅需考虑过控的成本,此时,误差(过控量)与后果(过控代价)可能接近线性。但若误差导致欠控,甚至造成大停电,就需要考虑误差与后果之间的强非线性。
文献[31]以2011 年日本地震、海啸等自然灾害引发大停电、进而导致核泄漏的事件为例,分析了小概率高风险事件对电力系统可靠性及经济性影响的严重性。其中,基础设施的缺陷、管理的失误、紧急处置的延误等因素共同引发了骨牌效应,造成了巨大灾难[32]。该文指出,安全评估应遵循风险观点,例如将风险定义为事件发生的概率与发生后损失值的乘积。在事件发生前,可以通过风险概念来量化评估对不同样本的关注度。
类似的,算法误差分布特性的经济影响,也由误差的概率及其经济代价两者共同决定。即使误差发生的概率很小,但若该算例误差的代价非常高;或者虽然误差发生的代价很低,但其发生的概率很大,这2 种情况都可能是高风险者。反过来说,既不应该单凭误差样本概率的大小,也不应该单凭误差样本的代价大小,作为对算例关注度排序的依据。总之,对不同样本的关注程度,应该依据其风险值,无须考虑的只是低风险的算例,而非误差小者。
但是,传统指标都不能反映上述复杂关系,故无法准确反映由于算法误差而潜在的风险,从而误导了相关决策。
2 评估电力系统算法误差的风险指标
2.1 误差的定义
误差通常被定义为待评估的值与真值之差:

式 中:em、y̑m、ym分 别 为 样 本m的 误 差、估 计 值 和 真值;m为样本号。
对于算法而言,y̑m为待评估算法给出的计算结果,如风电预测算法所求得的功率预测值、暂态稳定分析方法所得稳定性结论等;ym则取尽量接近实际的值,如实际的风电功率值、实际的暂态功角稳定裕度等,或被公认为精度最高的算法之一的计算值[33]。
2.2 算法的误差风险指标
2.2.1 单个样本的误差风险指标
基于风险观点,将样本m的误差风险指标定义为:

3 误差风险指标的计算方法
3.1 风电预测算法误差评估中的误差风险指标计算方法
文献[5]指出,对风电功率预测算法的误差进行评估时,必须区分误差的符号,否则就会误导预防控制(如备用容量)及紧急控制(如切机及切负荷)的配置,影响电力系统的可靠性及经济性。为此,在计算误差的代价时,对于正误差的算例,取为应对风电波动而额外安排的备用容量(设按功率缺额的x配置)成本A;对负误差的算例,则取为弃风损失B。因此,代价cm可表示为:

文献[5]按式(3)计算样本集整体的预测误差风险值R,对不同的预测模型进行了评估,并分析了当A、B取不同比例时各模型预测质量的变化情况。
3.2 暂态稳定分类器框架性能分析中的误差风险指标计算方法
3.2.1 误差评估准备
在暂态稳定分析的多输出分类器中,根据算例样本稳定性的量测值(输出分档结果)与真值(实际裕度区间)的关系,存在“正确分类”“风险性误分类”和“降效性误分类”3 类;而未被识别为该3 类的样本则为“不能确定类”。
3.2.2 分类器的总误差风险指标
理论上分类器样本全集Ω中每个样本对应的代价cm都需单独计算,而概率pm均为样本总数N的倒数,故由式(3)求得总风险值为:

对于同一Ψij中的各样本的代价可视为相等,并选一个典型值cij近似替代,以提升整体计算效率。为此,需要给出6×7 个对应的cij值,并将式(7)改写为:

式 中:nij、pij、cij分 别 为 子 集Ψij的 样 本 数、概 率 和代价。
进一步,可将6×7 个分类子集Ψij中具有相同风险定性特性的Ψij合并,得到8 个评估子集。上标表示{实际定性特性,分类定性特性}序列,其中,S 代表稳定,U 代表失稳。例如,将分类风险非常小的那些Ψi=j合并为同一评估子集Ωi=j;将必须以增加计算量的代价,调用精确的IEEAC 算法,获取正确结果的那些Ψj=7合并为同一评估子集Ωj=7。具体分类结果参见表1。
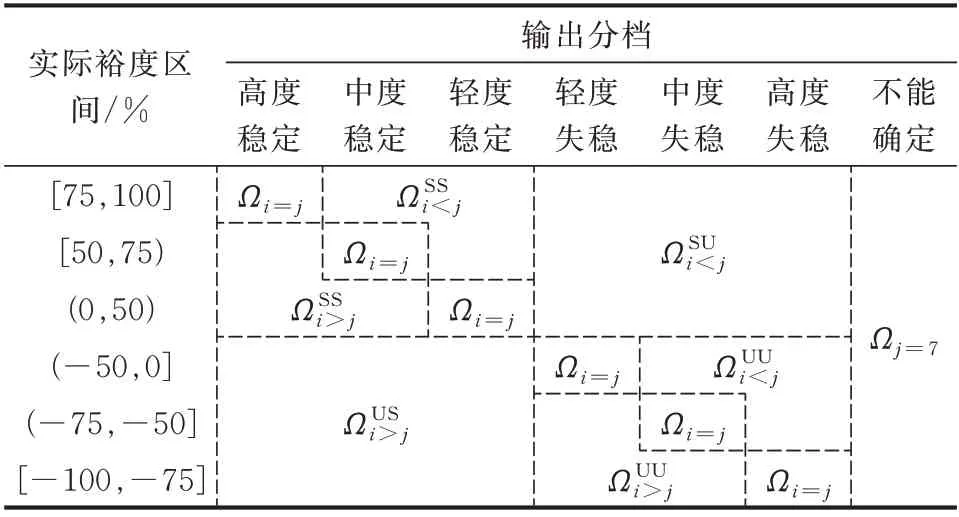
表1 CF-7 的分类结果Table 1 Filtering results of CF-7
3.2.3 不同分类样本集的代价
将样本分类为不同的评估子集后,不但从风险的观点反映了降效性及风险性2 类误分类在工程应用中的不同内涵,并且计及了误差大小对工程影响中的非线性。当然也可以直接按分类子集Ψij来提高分类总风险的计算精度,但一般并无必要。下面针对表1 中的不同评估子集分别讨论。
1)正确分类的样本集Ωi=j,对应的代价ci=j为零值,不再进行风险分析。
2)风险性误分类的样本集Ωi>j,又分为以下3 个子集:
(1)实际情况与其分类均为稳定,但分类偏乐观的样本子集ΩSSi>j。这些样本的分类过于乐观,但由于对实际指定的故障并不需要控制措施,故其风险代价cSSi>j为零值。但系统在防范相继故障等更严重的故障上可能存在潜在风险,故可以适当指定其主动防御代价。
(2)实际情况与其分类均为失稳,但分类偏乐观的样本子集ΩUUi>j。若按分类结果安排这些样本的控制量,就只能依靠额外的校正控制量来维持系统稳定,故欠控风险代价cUUi>j较大。
(3)实际失稳、却被分类为稳定的样本子集ΩUSi>j。此类样本不被配置预防控制措施和紧急控制,故障一旦发生,只能依靠校正控制来应对,系统甚至由于这类控制的时效低下而失稳。因此,对应的风险代价cUSi>j最大。
3)降效性误分类的样本集Ωi (1)实际情况与其分类均为稳定、但分类偏悲观的样本子集ΩSSi (2)实际情况与其分类均为失稳、但分类偏悲观的样本子集ΩUUi (3)实际稳定、却被分类为失稳的样本子集ΩSUi 4)未能明确分类的样本集Ωj=7。这些样本将通过详细分析获知精确的裕度,代价为零值,但会影响分类器的效率。 3.2.4 误差风险指标的求取及其矩阵化表达 根据上述讨论计算出各样本子集的代价cij,即可由式(8)求得CF-7 的风险值为: 以杜绝风险性误分类为前提,构建CF-7。比较按误差风险指标值最小原则优化阈值前、后的总风险值。优化的初值按文献[13]的方法设定。 取IEEE 10 机39 节点系统为测试系统,模型及工况均采用该系统的原始数据[34]。算例分类器的训练集分别取各线路/母线三相瞬时短路或三相永久短路,故障清除时间τ在0.10~0.50 s 内随机产生。另选随机生成的136 个算例作为测试集(见附录B 表B1)。仿真软件为EEAC 商品软件Fastest Ver 3.0.11。 根据3.2.3 节设置代价cij的取值,这里对各误差情形均做出一定的简化:针对Ωi 基于专家系统获取CF-7 阈值的方法见文献[13],具体的规则与阈值见附录C 表C1 和表C2;分类结果见附录C 表C3,统计出的误差概率矩阵P为: 由式(9)可求得初始的总风险值R为74.308 4。根据各分类的rij中数值较大者(rSS21=73.529 0 和rUS43=0.735 3)调整阈值,经过1 次寻优后,R降低到0.066 2,满足了收敛要求(这里设定为1.0)。更多的有关信息见附录D 表D1、表D2 及表D3。 表2 比较了阈值优化前后的性能,仿真硬件为搭载英特尔i5-2400 处理器(3.10 GHz)的台式微型计算机,内存为8 GB,操作系统为64 位Windows 10。优化前的分类结果见附录D 表D4。 表2 阈值优化前后的分析性能比较Table 2 Comparison of analysis performance before and after threshold optimization 由于以杜绝风险性误分类为前提,且因果型特征量的引入又大大提高了分类的强壮性,从而确保不会发生高风险代价的误分类,使阈值优化前后的风险值都很小。一方面,误差风险指标指导下的阈值调整,进一步地降低了整体风险;另一方面,由于优化前少量属于Ωi 本文分析了传统误差指标的局限性,即单纯从概率的视角来评估算法的误差,而没有同时计及误差在该特定领域问题中的内涵。后者包括误差所对应的损失函数的非线性,以及对误差符号的敏感性。按传统误差指标来优化算法的结果是将小概率高风险事件排斥在评估算例集之外,而难以在优化中协调好经济性与可靠性。本文提出了基于误差风险概念的误差风险指标,同时计及了误差的概率分布,以及误差的非线性与误差的符号对经济性的影响,并通过将可靠性映射为机会成本,从而可以统一处理误差对可靠性及经济性的影响。误差风险指标很好地满足了各项要求,并有效克服了传统指标的局限性;对于需要考虑误差影响的非线性或符号敏感性的场合,具有更好的实用性。此外,按机会成本的概念,可以很好地协调决策的经济性与系统的可靠性。通过对电力系统同步稳定性的仿真分析,验证了按误差风险指标来评估算法精度的有效性及普适性。下一步将结合新型电力系统的充裕性,来验证误差风险评估的实用性。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
4 误差风险指标的应用实例
4.1 测试系统及算例


4.2 阈值优化结果对比

5 结语
